电磁-机电暂态混合仿真接口交互信息限制性分析

陈鹏伟， 陶 顺， 杨 洋， 肖湘宁

(新能源电力系统国家重点实验室， 华北电力大学， 北京 102206)

电磁-机电暂态混合仿真接口交互信息限制性分析

陈鹏伟， 陶 顺， 杨 洋， 肖湘宁

(新能源电力系统国家重点实验室， 华北电力大学， 北京 102206)

电磁-机电混合仿真可同时实现对大规模电力系统的机电暂态仿真和局部网络的电磁暂态仿真，本文首先分析了混合仿真分割求解的信息量交互基本需求，分别从电磁侧与机电侧两个方面比较了各自边界条件的限制性，并就电磁侧电流源等值形式与功率源等值形式进行了适用性分析。最后，通过基于PSCAD+C的混合仿真平台验证了上述相应分析结论。

电磁暂态； 机电暂态； 混合仿真； 交互信息； 等值约束

1 引言

电磁-机电暂态混合仿真旨在一次仿真过程中同时实现对大规模电力系统的机电暂态仿真和局部网络的电磁暂态仿真，可以在节省计算资源的前提下保证局部系统的仿真精度[1]。由于其自身特殊的工程应用价值，自20世纪80年代起，电磁-机电混合仿真便逐渐成为国内外研究的热点之一。目前，较为成熟的混合仿真技术主要是通过适当的接口将商用电磁暂态仿真软件与完善的机电暂态程序结合进行混合仿真[2,3]，但两者在模型处理、积分步长、计算模式等方面存在的诸多差异使得仿真接口成为混合仿真实现的关键，即如何设计合适的接口形式，以使本侧网络计算中充分考虑对侧网络信息，从而保证整体仿真的准确性[4]。

在已有的研究中，基本采用等值的方式提供边界条件，等值电路的形式已基本确定，但等值参数求取算法仍在完善中[5]。机电侧计算是以相量形式进行的，因此电磁侧多以基波等值为主，如功率负荷(源)、注入电流源或诺顿(戴维南)等值电路形式，如何在满足实时仿真计算复杂度限制的情况下从电磁侧瞬时值计算结果中准确提取出基波相量是混合仿真一个关键的技术难点，尚需完善。电磁侧计算时机电侧多采用多端口戴维南(或诺顿)电路来等值，但戴维南(或诺顿)电路仅有基波等值信息，且在一个交互步长内机电侧系统等值电源以恒压源或恒流源形式出现，缺失其余暂态过程的信息。为了提供更广频率范围的等值信息，有学者提出机电侧系统采用频率相关的等值形式[6]，但该等值方法距离工程的实际应用仍较为遥远。

现有国内外混合仿真研究成果多针对混合仿真异构平台实现、仿真精度改善技术等问题。文献[5]明确了混合仿真的两个基本要求及面临的实质难题，包括分网方案、边界条件与对侧等值等。文献[6]针对机电侧系统等值，用算例验证了频率相关等值的必要性。文献[7]提出了预估校正的精度改善思路，以修正接口引入的延时与数值扰动误差，并应用于RTDS/并行机构成的异构混合仿真平台。文献[8]从串并行交互时序角度，分析了时序交互导致的误差。但是，在交互信息自身限制性方面尚无文献进行机理性的分析与讨论，而该部分内容恰是混合仿真技术改进与精度提高的重要基础。本文首先分析了混合仿真分割求解的信息量交互需求，然后分别从电磁侧与机电侧两个方面比较了各自等值形式的限制性，并就电磁侧电流源等值形式与功率源等值形式进行了各自的适用性分析；最后，利用基于PSCAD+C的电磁-机电混合仿真平台验证了上述相应分析结果。

2 网络分割求解的信息交互需求

电磁-机电混合仿真本质上是通过接口将系统划分为电磁子系统与机电子系统并分割求解的过程，因而在单侧计算时需要对侧系统在接口处提供恰当、充分的边界条件，即交互信息。

给定的电力系统如图1所示。其中YS与YE分别表示机电侧网络和电磁侧网络的导纳阵，US与UE分别表示机电侧网络和电磁侧网络的节点电压，hS与hE分别表示机电侧网络和电磁侧网络的等值电流源(用于简化发电机节点的注入)，接口联络线电流为Im，接口电压为Um，矩阵p与q分别表示机电侧网络和电磁侧网络中任意节点同接口联络线之间的节点-支路关联矩阵。

图1 系统分割求解示意图Fig.1 Segmentation process for system solving

分别求解机电侧网络和电磁侧网络，可以得到各自的网络方程：

YSUS=hS-pIm

(1)

YEUE=hE+qIm

(2)

接口节点同时存在于机电子系统和电磁子系统中，因而接口处电压应满足约束条件：

Um=pTUS=qTUE

(3)

联立后，可得：

(4)

根据式(4)求出接口电流Im后，即可反推求得各子网节点电压以及接口电压Um，可见接口电流Im是网络分割求解的关键，而接口电流的准确求解依赖于两侧网络参数及两侧系统发电机注入电流。

需要指出，对于实际混合仿真平台而言，上述网络分割求解的条件往往无法直接满足。电磁暂态仿真一般基于成熟的商用电磁暂态仿真软件(RTDS、PSCAD等)，其封装特性使得电磁侧子网络的导纳阵YS无法直接获得，为了获得准确的接口电流Im，只能从电磁暂态仿真结果中获取。因此需要机电侧子网络在电磁暂态计算中进行等值处理，以等值电路代替上述所需机电系统导纳阵及发电机注入电流，从而获得瞬时值形式的接口电流im，继而获得用于机电暂态计算的接口电流基波相量形式Im，传递给机电侧系统用于机电暂态计算。可以发现，采用混合仿真方式，上述式(3)与式(4)的接口电压与电流约束条件不再同时满足，而是交替满足。此外，根据交互时序的不同，混合仿真可分为并行与串行仿真两种。采用并行时序时两侧系统均有一个交互步长延时，如图2所示；串行交互时一侧系统也不可避免有一个交互步长延时，这就导致分割求解所用边界条件不能严格对应。

图2 并行交互时序及计算示意图Fig.2 Diagram of parallel interaction timing sequence

因此，在分割求解直接需求无法满足的情况下，使用其他边界条件作为替代时必然需要考虑其限制性。

3 电磁侧等值信息的限制性分析

机电暂态仿真采用的是单相准稳态模型，计算是以相量形式进行，因此电磁子系统多以基波等值为主，一般有功率源(负荷)、注入电流源或诺顿(戴维南)等值电路三种形式，如图3所示。

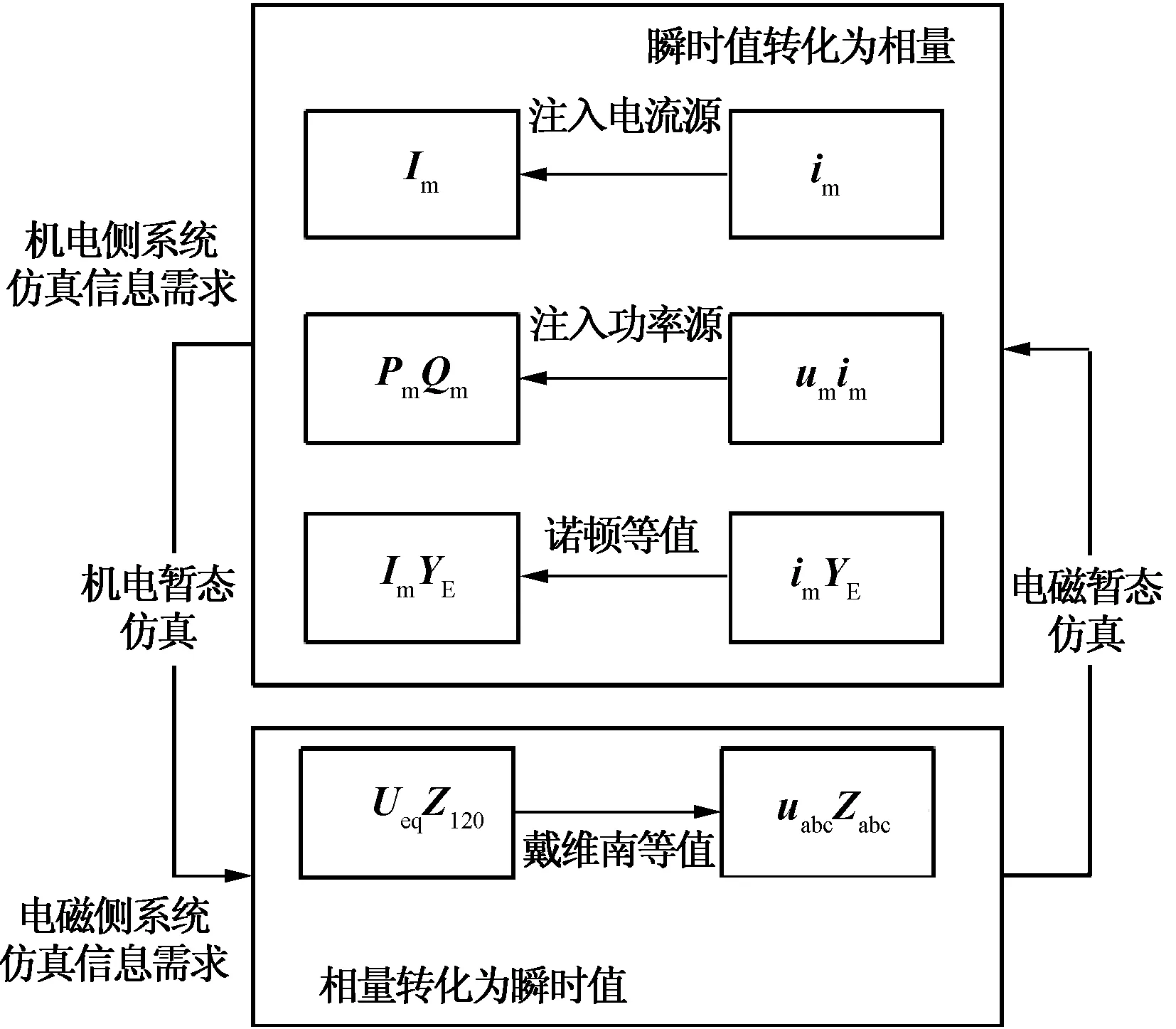
图3 混合仿真交互信息传递示意图Fig.3 Diagram of transinformation in hybrid simulation

(1)电流源等值

若电磁侧系统采用电流源Im作为等值形式，由于交互延时作用，可表示为Im(tj-1)，则机电侧网络方程为：

YSUS(tj)=hS(tj)-pIm(tj-1)

(5)

式中，tj表示当前时刻；tj-1表示一个交互步长前的时刻。

接口等值注入电流可以直接合并到机电网络方程右端对应节点上，计算直接简单。如何准确地从瞬时值形式的接口电流im中提取出基波相量Im是该种等值形式的关键，特别是注入电流绝对相位的提取。需要指出，相量概念一般仅适用稳态波形，而基于机电侧等值的电磁暂态仿真中，注入电流Im的求取准确度又依赖于机电子系统等值电路的准确性。

电流源等值物理本质上是在单步机电暂态计算过程中对机电子网络与电磁子网络完全割离。采用上一个交互步长计算出的注入电流等来进行本次机电暂态计算时，并未考虑对侧电磁网络的特性和时延影响，这点与式(3)和式(4)所体现的网络分割求解的需求是矛盾的。

多端口情况下，电流源的等值形式实质上是以端口为基准，在一个机电仿真步长内将电磁侧系统划分为多个子系统，则注入机电系统的总功率可利用梯形法近似为：

(6)

式中，Umi表示机电暂态仿真计算出的端口i的接口电压；ΔUmi表示当前时刻与前一步长计算的接口电压变化量；Imi表示电磁侧传递至机电侧的端口i接口电流；n表示接口端口总数。可以发现，在一个交互步长内，电磁侧多端输入功率的波动情况完全依赖于机电侧系统特性。对于含HVDC的电磁子系统而言，其端口之间存在功率输入与输出的强耦合关系，端口功率不完全依赖于机电系统。故多端口情况下，电流源等值的不适用性会有所减弱，且会随着端口数的增加而进一步体现。

另外一方面，机电子系统接口电压可以表示为：

Um=E(hS)-ZeqIm

(7)

式中，E(hS)表示各发电机注入电流作用在各接口的等效戴维南电势；Zeq表示接口等效阻抗阵。若忽略发电机效应，则接口电压计算误差可近似为：

(8)

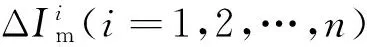
可以发现，多端口情况下，接口电流相量提取误差在各接口会存在累积作用，接口数目的选定应与接口相量提取算法精度及仿真精度需求相适应。为得到上述接口数目与精度间的关系，分别令：

由式(8)可得：

(9)

(10)

(2)诺顿等值

设电磁侧子系统诺顿电路中的等值电流源和等值导纳分别记作Im(tj-1)与YE，则机电侧网络方程为：

[YS-pYEpT]US(tj)=hS(tj)-pIm(tj-1)

(11)

注入的等值电流Im是接口节点电压的线性函数，求解机电侧网络方程左侧的导纳矩阵和右侧的发电机注入电流列向量都要作相应修正，计算过程稍微复杂一些。机电子系统节点电压US会受到电磁侧网络特性的影响，集中体现在等值导纳YE上，因而它更符合系统的物理本质，但其中等效电流源仍不可避免地无法满足网络分割求解的无延时需求。

诺顿电路属于线性网络的一种等值形式，但电磁侧经常含有复杂的非线性元件和参数(含FACTS元件或HVDC系统)，甚至可能是一个无源系统，严格来说它难以满足网络诺顿等值的基本条件(相量提取不准确，无法形成诺顿等值)，因而电磁侧采用诺顿等值电路形式只能保证一定的近似性，特别是暂态过程中可能会带来较大的仿真误差，即YE不足以表征电磁网络而导致式(3)接口电压的计算误差。

(3)功率源等值

以功率源S(tj-1)作为电磁侧等值信息，则机电侧网络方程求解会转化为非线性方程组求解问题，

(12)

式中，S*(tj-1)为S(tj-1)共轭形式。

由于仿真计算时一般采用数值迭代方式求解，功率源等值会相应增加机电暂态计算的复杂度。此外，除由上一步长仿真结果计算得到接口注入功率所带来的边界条件不准确外，其在本质上仅是为接口电压Um和接口电流Im提供了共同的约束关系而不是提供各自独立的约束关系，因而会存在非唯一解情况，以下给出证明。

以单端口为例，对式(7)进行增阶扩展，即采用计算机计算所采用的实、虚部分解形式，并经线性变换后，可以得到接口电压Um改写形式：

(13)

式中，a1和a2是与发电机注入电流hS有关的常量(一个机电步长内)；k1～k4是与接口有功功率P和无功功率Q有关的常量。

已知有功功率P和无功功率Q下机电侧网络解的问题就转化为式(14)所示非线性方程组的解的分布问题：

(14)

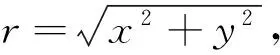
(15)

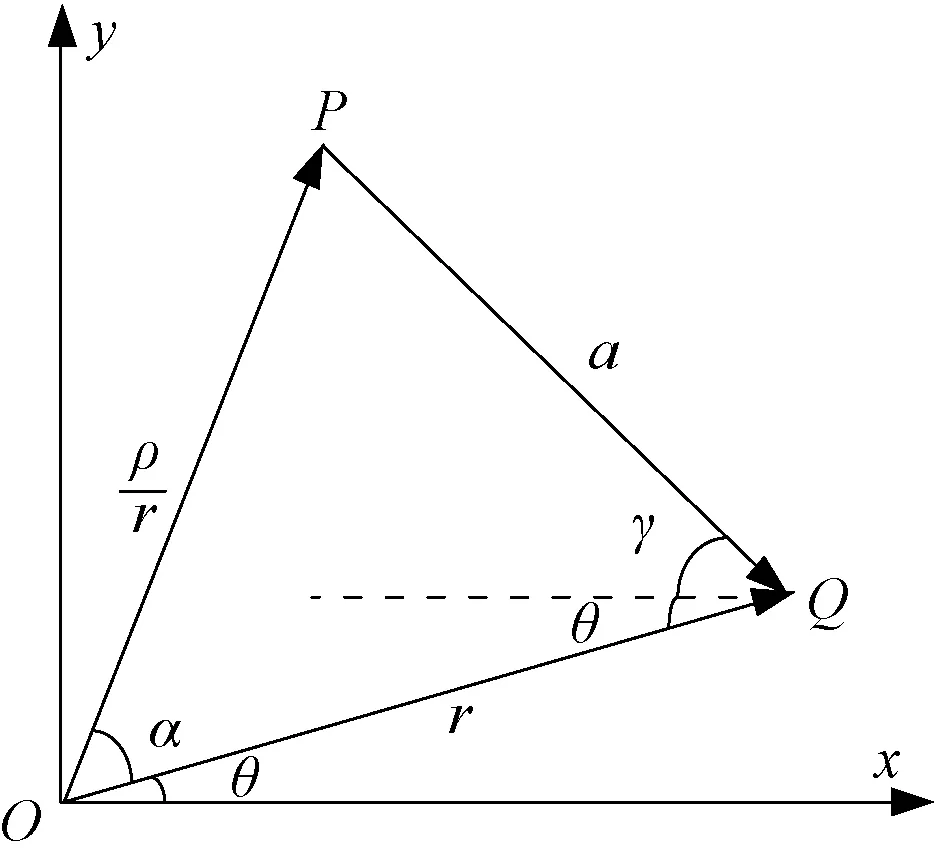
图4 方程解示意图Fig.4 Solution of equation

根据余弦定理，有

(16)

式(16)中除了r外，其余均为常数，可以解得:

(17)

分析式(17)右侧可知，由于右侧恒大于零，因此，r存在两个解，记为rmax和rmin。确定r后，根据正弦定理，有

(18)

式中，α、ρ和γ为常数；θ可解。

对于更一般情况，A=[k1,k2;k3,k4]为可逆矩阵时，它作用在[cosθ,jsinθ]T时仅是仿射变换，设Ae1=ε1，Ae2=ε2，其中e1=(1,0)T，e2=(0,1)T，则A(cosθ,sinθ)T=ε1cosθ+ε2sinθ，所以，若设ρej(α+θ)=A(cosθ,jsinθ)T，则ρ和α均为与θ相关的常数，不再赘述。从以上分析可知，当机电侧系统只接收接口位置传递过来的功率信息时，对于特定的一组功率值，其解并不唯一，就电压的幅值而言，存在两个可行解。

此外,功率源等值需要同时根据接口提取电压相量与接口电流相量计算得到，则在暂态故障发生及切除时刻，由于暂态非平稳情况下相量提取的固有误差，功率提取的精度一般会小于单一电流相量的提取精度。故单端口情况下，在相量提取误差范围内，功率源等值精度要低于电流源等值。

4 机电侧等值信息的限制性分析

机电侧向电磁侧提供计算的边界条件，理想情况下应能处理仿真系统中谐波、三相非对称和非周期分量等，并具有宽频甚至全频域响应特性，即宽频等值。但实际情况下，机电暂态计算不考虑装置级的电磁暂态过程，没有系统谐波信息，在故障发生时刻也不考虑电气量非周期分量，机电暂态仿真对系统非对称情况的处理也与电磁不同[8]。由于等值方法可行性与实用性的限制，目前最常用的等值形式为基频等值-戴维南(或诺顿)等值电路，但存在以下不足。

(1)线性等值限制

戴维南等值属于线性网络的一种等值形式，但机电侧含有非线性元件或动态综合负荷时无法保证等值准确性，尤其在暂态过程中会带来一定的仿真误差。因此接口母线位置选取，即机电侧系统与电磁侧系统的界限划分应有所考虑，且动态综合性负荷应远离接口母线，避免电磁侧暂态故障下造成动态综合性负荷偏离其稳态运行点过大的情况发生，从而减小戴维南线性等值偏差。

(2)参数求取限制

现有戴维南等值方法中，正、负和零序等值阻抗是提供给电磁进行不对称暂态故障仿真的重要基础。正序等值阻抗可以依赖于机电侧系统网络方程，但负、零序等值阻抗的求解均依赖于各自序网络，而各自序网络的建立同时依赖于网络拓扑与元件结构及参数。当机电侧发电机正、负序阻抗不相等或者母线带有动态特性综合负荷时，戴维南等值电路中的正、负序阻抗会不相等，因而经线性变换到 abc 相空间后，就会出现不对称矩阵，从而增加构造混合仿真接口的难度。

(3)准稳态模型限制

机电暂态计算是以相量形式进行的，而相量的概念是建立在“正弦稳态”或“准稳态”假定基础之上的，即认为电流、电压相量或者功率的变化是慢速的，仅考虑发电机模型、负荷模型和控制系统非调制量的动态变化，而不考虑输电线路调制量的动态变化，即不考虑输电线路暂态行为的激发特性。文献[9]详细分析了基于准稳态模型的相量计算方式在功率平衡上的误差，提出快速调制量和其微分、非调制量和其微分在平衡时刻的变化是造成“准稳态”假定误差的根源。其中，发电机变量(E′，EG，IG，δ等)、负荷变量(EL，IL)属于非调制量；输电线路的状态量为调制量，如线路母线电压相量和相角(U，δu)，线路电流相量和相角(I，δi)。

(4)频率表征限制

戴维南等值模型传递给电磁侧系统的等值电势一般是以电磁侧的时钟频率体现，而机电侧频率的变化通过戴维南等值电势的相位变化来体现。当系统处于稳态情况时，系统频率保持在基准频率附近，不会出现因频率引起仿真误差。对于系统动态过程，机电侧系统频率在基准频率附近摆动，戴维南相位以交互步长的周期变化，不能体现系统频率连续变化的特性。

5 仿真验证

5.1 仿真测试系统

分别利用基于PSCAD+C与RTDS+C的混合仿真平台进行单接口与双接口混合仿真验证。单接口仿真模型电磁侧为Cigre benchmark HVDC+贝杰龙参数HVAC的并联外送线路，并经PI型线路接入无穷大系统，机电侧为两台发电机组，具体如图5所示。双接口仿真模型以某实际系统为例，如图6所示，其中安顺换流站为整流站，肇庆换流站为逆变站，各自交流母线为混合仿真接口母线。分别取HVDC逆变侧交流母线作为暂态故障点，暂态故障类型设为三相对称接地故障，故障持续时间为0.1s。

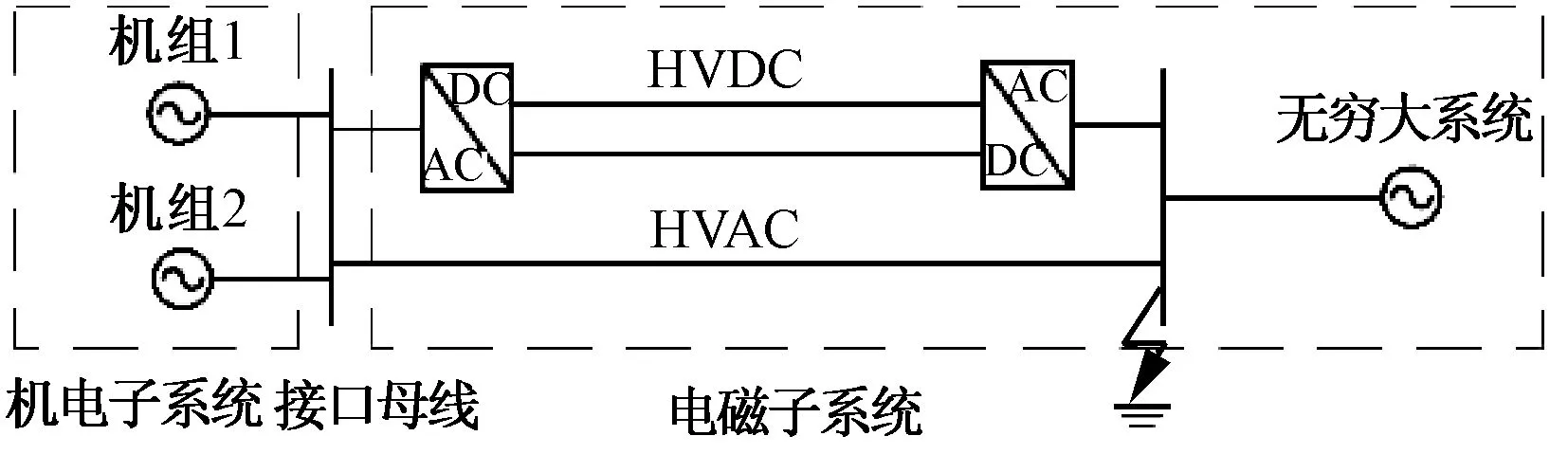
图5 交互信息限制性测试系统(单接口)Fig.5 Test system for transinformation limit (1 interface)

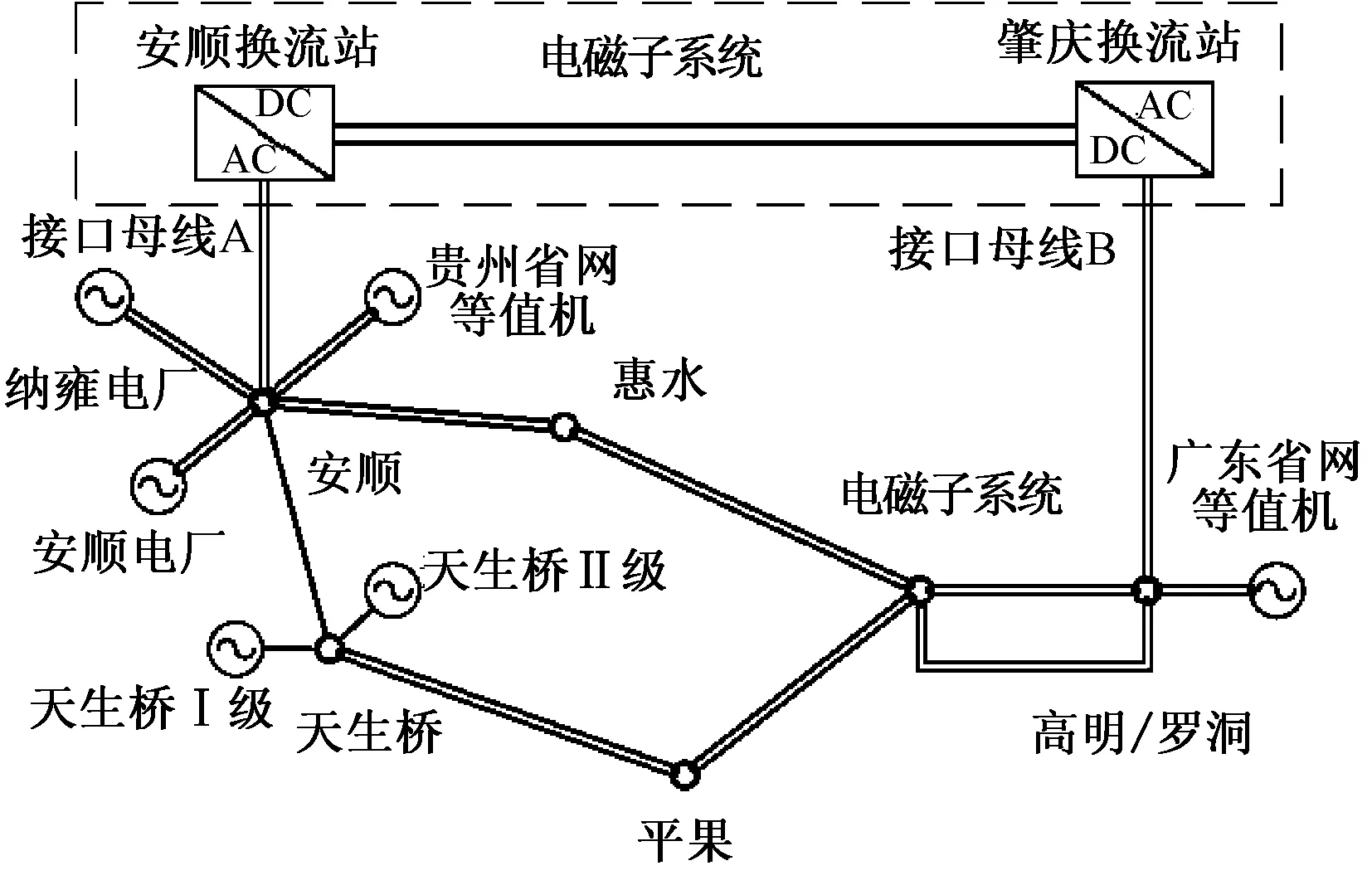
图6 交互信息限制性测试系统(双接口)Fig.6 Test system for transinformation limit (2 interfaces)

5.2 仿真验证

为验证电磁侧不同等值形式对仿真结果的影响，考虑到诺顿等值应用到含HVDC的电磁子系统困难性，仅对电流源与功率源两种等值形式的仿真结果进行了比较。考虑到现有各相量提取方法的准确性与实时性[10]，相量提取及功率计算均采用dq120均方根法[11]。电流源等值混合仿真、功率源等值混合仿真与全电磁仿真的仿真结果如图7～图9所示。

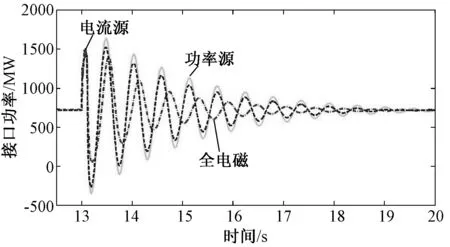
图7 接地电阻0.5Ω时电磁侧不同等值形式下接口有功功率仿真对比Fig.7 Comparison of interface active power using different equivalent types for electromagnetic subsystem with ground resistance of 0.5Ω

图8 接地电阻0.1Ω时电磁侧不同等值形式下接口有功功率仿真对比Fig.8 Comparison of interface active power using different equivalent types for electromagnetic subsystem with ground resistance of 0.1Ω

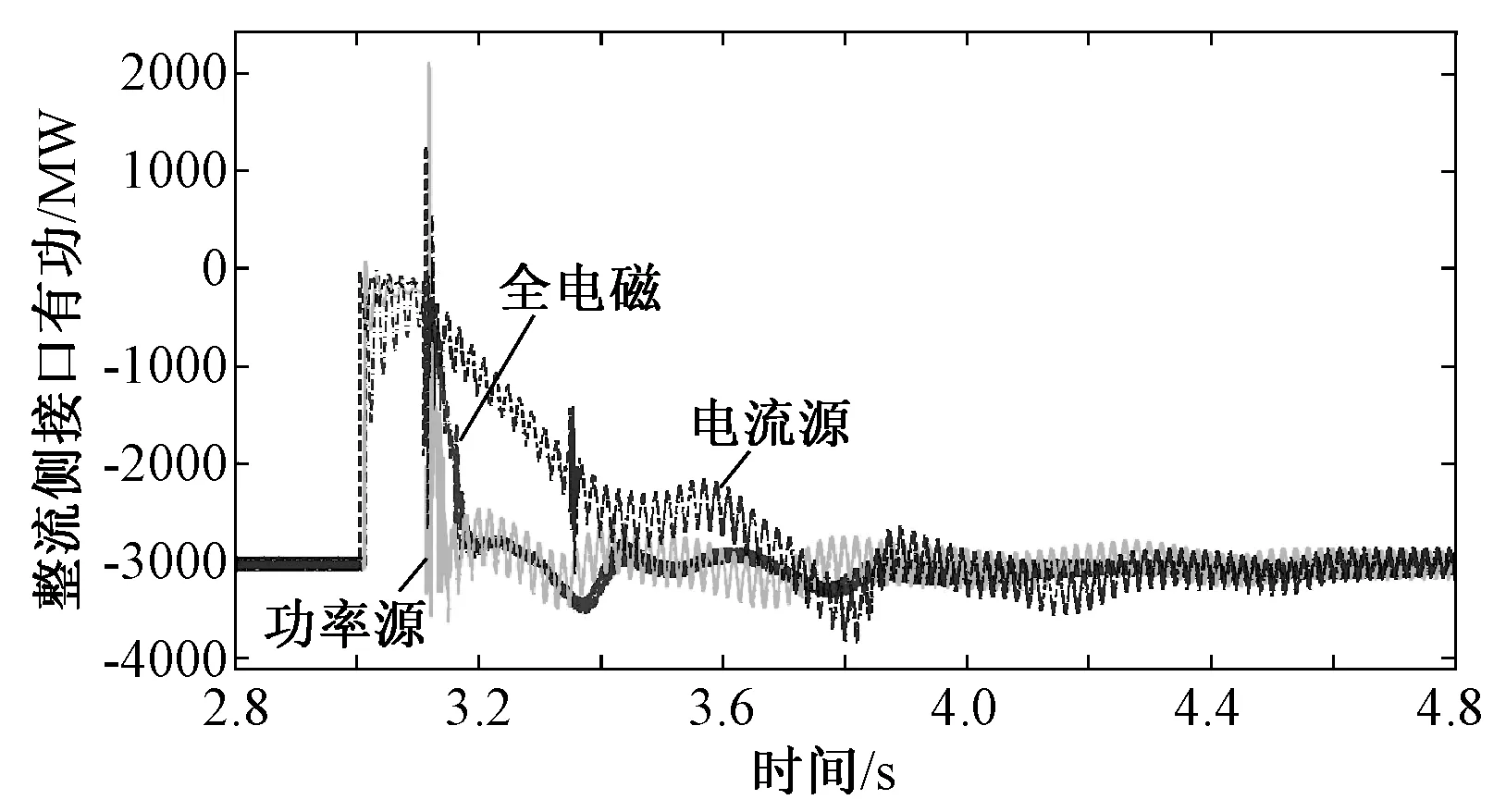
图9 接地电阻0.5Ω时电磁侧不同等值形式下安顺站接口有功功率仿真对比Fig.9 Comparison of Anshun interface active power using different equivalent types for electromagnetic subsystem with ground resistance of 0.5Ω

(1)单接口系统验证

由图7和图8可以看出，对于接口注入有功波形的衰减收敛特性，在接口状态相量可以准确测量的情况下(无穷大电源保证了频率与相位稳定性，保证了相量测量精度)，电流源等值形式仿真精度高于功率源等值。这是由于电磁侧子系统采用电流源等值时，电磁侧对机电侧提供准确的约束-接口电流，机电侧为电磁侧提供准确的电压约束，而采用功率源等值，上述交替形成的电压电流约束消失。

(2)双接口系统验证

由图9安顺换流站接口功率波形可以看出，双接口下，由于直流系统功率耦合作用，电磁侧电流源等值形式的适用性减弱，功率源等值形式具有更高的仿真精度，与第3节分析一致。但功率源本身存在的双解并参与迭代计算这一特性，在暂态情况下也会导致机电暂态迭代计算时出现无法收敛的可能。

6 结论

本文首先分析了网络分割求解的基本信息量需求，在混合仿真无法满足基本需求的前提下，分别从电磁侧与机电侧两个方面比较了各自交互信息的限制性，并就电磁侧电流源等值形式与功率源等值形式进行了适用性分析。最后，利用基于PSCAD+C的电磁-机电混合仿真对含HVDC与HVAC交直流并联系统进行了电磁侧不同等值形式的仿真验证。理论分析与仿真结果表明：

(1)现有混合仿真单侧等值交互信息均无法完全满足网络分割求解基本需求，均存在自身限制性；

(2)对于单端口情况，电磁侧电流源等值仿真精度高于功率源等值形式，但在多端口情况下其适用性有所减弱；

(3)多端口混合仿真接口数目受接口相量提取算法精度、端口阻抗特性及仿真精度需求的共同制约，且数量不宜过多。

[1] Heffernan M D, Turner K S, Arrillaga J, et al. Computation of A.C.-D.C. system disturbances - Part I: Interactive coordination of generator and convertor transient models [J]. IEEE Transactions on Power Apparatus and Systems, 1981, PAS-100(11): 4341-4348.

[2] 朱旭凯，周孝信，田芳，等 (Zhu Xukai, Zhou Xiaoxin, Tian Fang, et al.). 基于电力系统全数字实时仿真装置的大电网机电暂态-电磁暂态混合仿真(Hybrid electromechanical-electromagnetic simulation to transient process of large-scale power grid on the basis of ADPSS)[J]. 电网技术(Power System Technology), 2011, 35(3): 26-31.

[3] 张树卿，童陆园，薛巍，等(Zhang Shuqing, Tong Luyuan，Xue Wei，et al.). 基于数字计算机和RTDS的实时混合仿真(Digital computer and RTDS based real-time hybrid simulation)[J]. 电力系统自动化(Automation of Electric Power System), 2009, 33(18): 61-66.

[4] 岳成燕, 田芳, 周孝信, 等(Yue Chengyan，Tian Fang，Zhou Xiaoxin，et al.). 电力系统电磁暂态-机电暂态混合仿真接口原理(Principle of interfaces for hybrid simulation of power system electromagnetic-electromechanical transient process)[J]. 电网技术(Power System Technology), 2006, 30(1): 23-27.

[5] 张树卿, 梁旭, 童陆园, 等(Zhang Shuqing，Liang Xu，Tong Luyuan，et al.). 电力系统电磁/机电暂态实时混合仿真的关键技术(Key technologies of the power system electromagnetic/electromechanical real-time hybrid simulation)[J]. 电力系统自动化(Automation of Electric Power System), 2008, 32(15): 89-96.

[6] Annakkage U D, Nair N K C, Liang Y, et al. Dynamic system equivalents: A survey of available techniques [J]. IEEE Transactions on Power Delivery, 2012, 27(1): 411-420.

[7] 张树卿，童陆园，郭琦，等(Zhang Shuqing, Tong Luyuan，Guo Qi，et al.). SMRT交直分网混合实时仿真接口关键技术与实现 (Key techniques and implementation of SMRT hybrid real-time simulation employing AC/DC partitioning scheme)[J]. 南方电网技术(Southern Power System Technology), 2015, 9(1): 39-46.

[8] 柳勇军(Liu Yongjun). 电力系统机电暂态和电磁暂态混合仿真技术的研究(Study on power system electromechanical transient and electromagnetic transient hybrid simulation)[D]. 北京: 清华大学(Beijing: Tsinghua University), 2006.

[9] 黄胜利 (Huang Shengli). 时变动态相量理论在电力系统分析中的应用(Application of time-varying dynamic phasor theory in analysis of electric power system)[D]. 北京: 中国电力科学研究院(Beijing: China Electric Power Research Institute)，2002.

[10] Chen Pengwei, Yang Yang, Tao Shun, et al. Research on an improved matrix pencil method for phasor extraction [A]. International Conference on Power System Technology (POWERCON) [C]. 2014. 1314-1319.

[11] 李秋硕, 张剑, 肖湘宁, 等 (Li Qiushuo，Zhang Jian， Xiao Xiangning，et al.). 基于 RTDS 的机电-电磁暂态混合实时仿真及其在 FACTS 中的应用(Electromechanical-electromagnetic transient real time simulation based on RTDS and its application to FACTS) [J]. 电工技术学报 (Transactions of China Electrotechnical Society)，2012，27(3): 219-226.

Analysis of transinformation limit for electromagnetic-electromechanical hybrid simulation

CHEN Peng-wei, TAO Shun, YANG Yang, XIAO Xiang-ning

(State Key Laboratory for Alternate Electrical Power System with Renewable Energy Sources, North China Electric Power University, Beijing 102206, China)

The electromagnetic-electromechanical hybrid simulation can realize the electromechanical transient simulation for large-scale power grid and the electromagnetic transient simulation for target system simultaneously. In this paper, the basic requirements of transinformation for grid segmentation process in hybrid simulation are firstly analyzed. From two sides of electromagnetic and electromechanical subsystems，the limits of boundary conditions are also compared respectively, especially the applicability of equivalent current source and power source for electromagnetic subsystem. In the end, the hybrid simulation platform based on PACAD+C is used to verify the above corresponding analysis conclusion.

electromagnetic transient; electromechanical transient; hybrid simulation; transinformation; equivalent constraints

2015-07-01

中央高校基本科研业务费专项资金资助项目(2015XS22)

陈鹏伟(1992-)， 男， 安徽籍， 博士研究生， 研究方向为电力系统仿真与微电网技术； 陶 顺(1972-)， 女， 湖南籍， 副教授， 研究方向为电力系统仿真、 电能质量与主动配电网等。

TM743

A

1003-3076(2016)05-0001-07