基于自适应FrFT域扩展Hurst指数的超/特高压输电线路单相瞬时故障全拍频检测
张宇辉, 吴家明, 武东斌, 王劼妍
(东北电力大学电气工程学院, 吉林省 吉林市 132012)
基于自适应FrFT域扩展Hurst指数的超/特高压输电线路单相瞬时故障全拍频检测
张宇辉, 吴家明, 武东斌, 王劼妍
(东北电力大学电气工程学院, 吉林省 吉林市 132012)
超高压输电线路拍频判据通常认为瞬时故障必伴随强拍频振荡,本文通过分析拍频振荡起振条件,发现线路在瞬时故障下可能发生弱拍频现象,导致传统拍频判据误判。针对这一问题,提出了基于自适应FrFT域扩展Hurst指数的单相瞬时故障全拍频检测方法,提取断开相电抗器电流的非线性特征作为特征量。首先,根据峰值扫描法快速确定最佳阶次FrFT域(u域),通过FrFT域的能量聚集特性放大时域故障信号的非线性特征,利用扩展Hurst指数捕获该特征用于故障辨识。瞬时故障伴随强拍频现象时,该方法具有更优异的噪声免疫力,可直接用于对含噪信号的故障性质快速可靠识别;若伴随弱拍频现象时,该方法仍能保持高度的有效性。大量EMPT仿真证明了方法的有效性和可靠性。
FrFT; 扩展Hurst指数; 拍频; 非线性放大器
1 引言
统计数据表明,大容量高压输电系统故障80%是以单相瞬时性故障形式存在[1-3]。传统定时限重合闸技术虽能确保系统暂态稳定性和供电可靠性,同时也存在盲目重合造成二次冲击的危险,因此,自适应重合闸技术对输电线路稳定运行具有重要的实际意义。
当前大容量超/特高压输电网通常配置定量的并联电抗器以抑制潜供电流,吸收无功功率,稳定系统运行电压。并联电抗器的引入,一方面改变了输电线路故障时电气量特征,限制了传统电压判据的实际应用[4,5];同时加速了电弧的熄灭,导致利用电弧特性进行故障识别难以实现,给自适应重合闸故障识别带来一定的困难[6]。对于带并联电抗器的输电线路,并联电抗器侧CT获取的断开相电流量的精度较PT获取的电压量高,更能满足故障性质识别要求[7]。目前多数瞬时故障拍频判据是以故障时必伴随强拍频振荡现象为前提,且没有考虑噪声对判据的影响,而现场录波时的噪声干扰必然存在,这就要求判据在保证可靠性的同时具有一定的抗噪能力。因此,弥补这两个方面的缺陷,对完善超高压线路的自适应重合闸体系十分必要。
基于拍频振荡的非线性特征,本文提出一种基于FrFT域扩展Hurst指数的全拍频检测方法,对伴随强拍频特征的单相瞬时故障,分析方法的可靠性与噪声免疫能力,对伴随弱拍频特征的单相瞬时性故障,验证方法的有效性,进一步消除传统拍频判据的识别盲区,为实现瞬时故障的可靠识别提供新的依据。
2 拍频振荡起振条件
拍频现象是带并联电抗器的超/特高压线路在瞬时性故障可靠熄弧后,故障电气量由于储能元件的初始储能引起的局部振荡现象[8],此时除工频分量外还存在自由振荡分量。在带并联电抗器单相瞬时性故障和永久性故障恢复电压阶段,并联电抗器电流i(t)可表示为:
(1)
式中,i1(t)表示瞬时性故障时断开相电流量;i2(t)表示永久性故障时断开相电流量。由此可知,自振分量与工频分量的频率、幅值差将直接影响拍频振荡的强弱。若在短时窗内近似忽略工频及自振分量的幅值衰减,可得:
(2)
式中,I、ω0分别为拍频振荡的幅值和频率。对于确定的超/特高压线路,ω0与线路并联补偿度k的关系为:
(3)
当自振分量与工频分量幅值相近并具有一定频率差时,单相瞬时故障下才能观察到强拍频振荡。以下几种情况时存在弱拍频振荡[9]。
(1)输电线路电压等级在750~1150kV时,线路的并联补偿度在0.9~1.0,采用近全补偿方式运行,此时自振分量频率接近工频,拍频周期长,并联电抗器电流在短时窗内存在弱拍频现象。
(2)并联补偿度与相间补偿度成一定关系时,工频分量幅值远小于自振分量,存在弱拍频振荡。
(3)自振分量的衰减受网络电阻影响,并联电抗器品质因数低会导致自振分量幅值衰减过快,拍频振荡持续时间短。
当上述几种情况发生时,弱分量被相对强的分量“淹没”,时域上难以直接检测出是否发生拍频振荡,导致基于强拍频特征的传统判据失效。换言之,传统拍频判据存在故障识别盲区,提出一种能够准确识别弱拍频振荡的检测方法具有实际意义。
3 自适应FrFT域
3.1 分数阶Fourier变换
FrFT是传统FFT的广义表述,其不再将信号表达局限在时域或频域,能够更加精确地描述电力系统中的非平稳信号[10,11]。定义时域信号x(t)的p阶FrFT为:
(4)
式中,核函数为:
(5)
式中,p可为任意实数;旋转角度α=pπ/2。应特别指出的是,p=0代表时域,p=1代表频域,此时FrFT就退化为传统的FFT。将FrFT变换理解为时频面的旋转算子,如图1所示。

图1 FrFT域Fig.1 Fractional Fourier transform domain
FrFT将时域信号投射到与时域轴夹角为α的u域上,在不同的变换域,时域信号会呈现出不同的能量聚集特性,故FrFT对难以直接检测的时域信号具有无法替代的变阶优势。鉴于此,适当调整p能放大瞬时性故障和永久性故障下电抗器电流的非线性特征差异,使弱拍频振荡检测成为可能。
3.2 峰值扫描法
寻找适合的阶数p是应用FrFT的关键技术。文献[12,13]通过求解chirp信号的调频率来估计最优阶数p,在一定能量的噪声背景下此类依靠确定经验公式来描述不同信号的方法精度不高。根据瞬时故障和永久故障下电抗器电流信号的特性,采用峰值扫描法自适应确定阶数p,其基本思路是一定范围内阶数p为变量扫描,求出待检信号的FrFT,形成信号能量在(p,u)平面的二维分布,捕捉峰值对应的p即认为是最优阶数。
4 扩展Hurst指数
随着分形理论的发展[14,15],Kantelhardt等发现单一尺度从整体描述非平稳信号存在粗糙度的不足[16],无法精确描述信号的局部非线性特性。传统Hurst指数具体步骤如下。
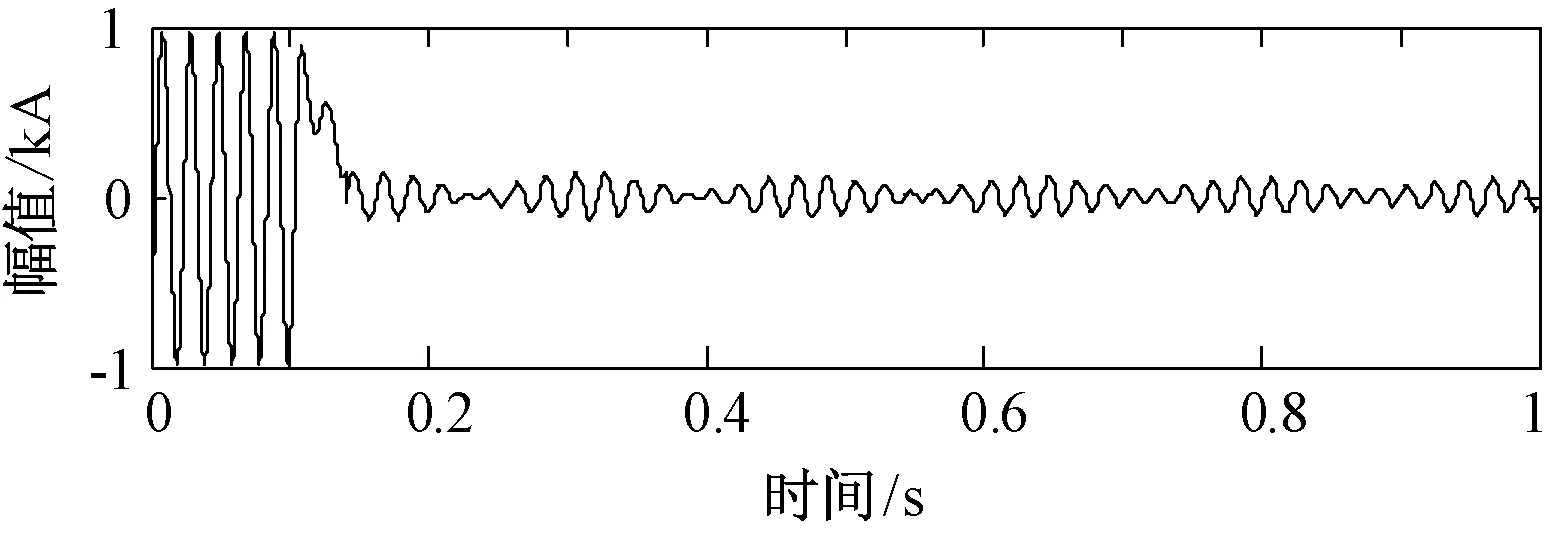
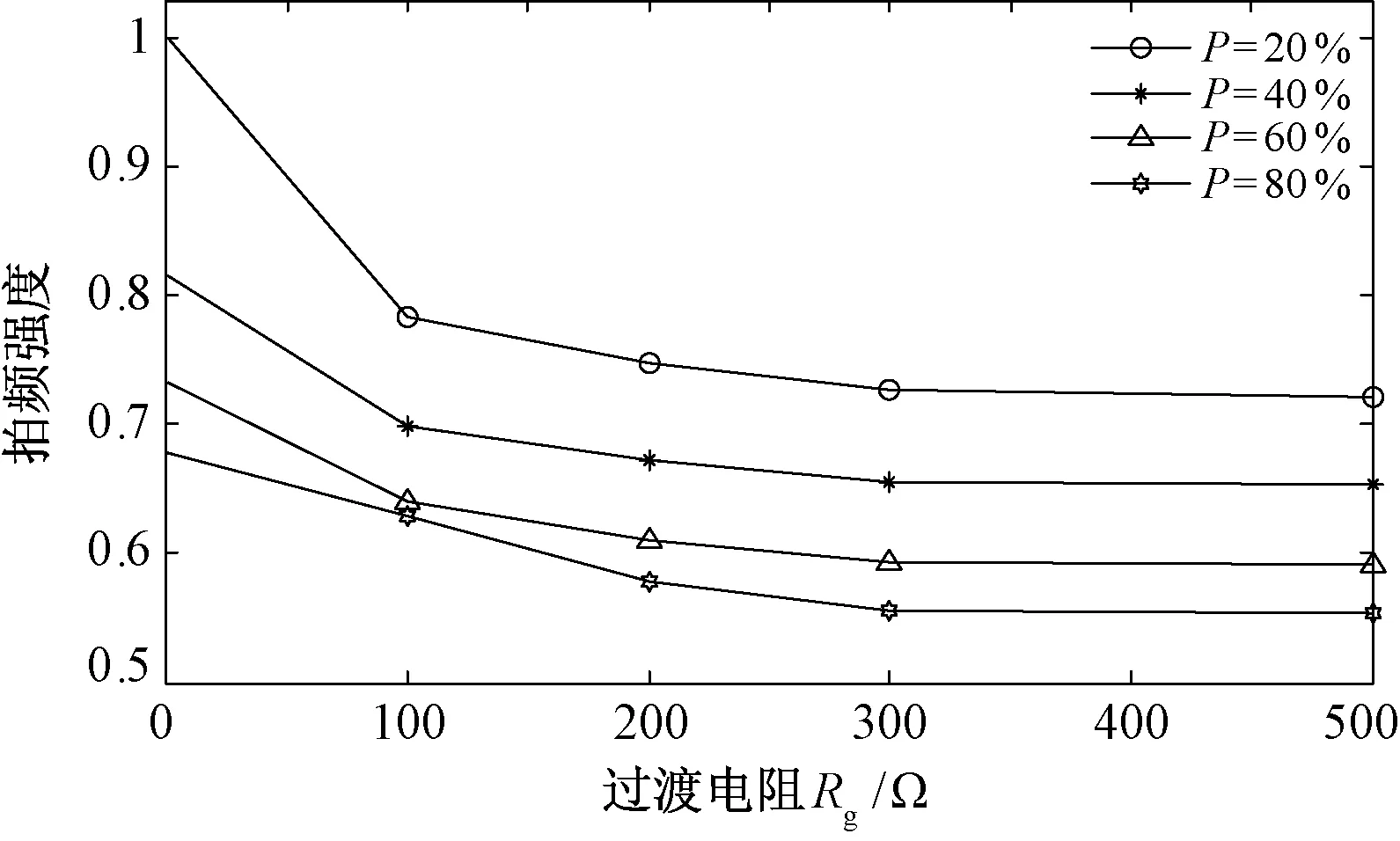
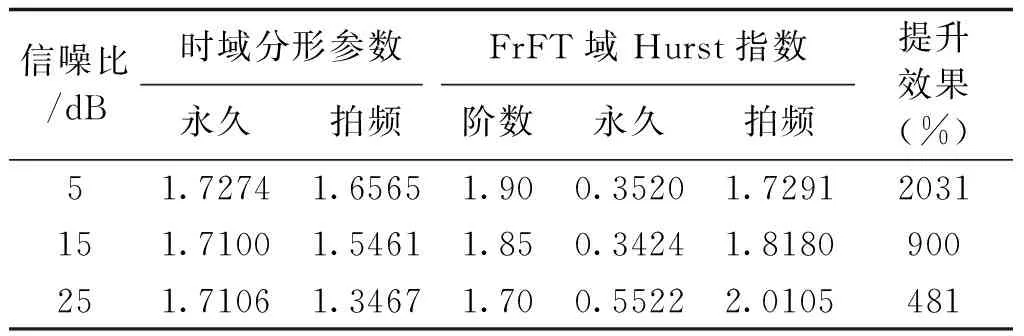
(1)对于不满足随机游走特性的时间序列{x(i),0 (6) (2)将新序列Y(i)以固定尺度k划分为互不重叠的Nk段子序列,其中Nk为: Nk=int(N/k) (7) 若Y(i)不能完全分解,则进行逆向分解得到2Nk段子序列以确保序列信息的完整性。 (3)采用最小二乘法对各子序列进行m(m=1, 2, 3,…)阶多项式拟合,求取子序列与其局部趋势项yi,fit的均方差: (8) 式中,i=1,2,…,Nk。 (9) 式中,i=Nk+1,Nk+2,…,2Nk。 (4)定义序列x(i)的波动函数为: (10) 解出Hurst指数为: (11) 对式(10)进行扩展,定义q阶波动函数为: (12) 波动函数具有类似非线性放大器的效果,不同的阶数q能不同程度地放大时间序列x(i)的非线性特征。对于微弱非线性特征,q取[-40,-50]内任一值均能得到良好的放大效果,本文取q=-45。本文将扩展Hurst指数作为故障下电抗器电流信号非线性特征的度量指标,为输电线路的故障识别提供现实依据。 5.1 仿真模型 采用文献[9]中的仿真算例,即如图2所示的1000kV双端带并联电抗器的输电系统进行EMPT仿真验证,其线路参数如表1所示。 图2 双端带并联电抗器输电系统Fig.2 Transmission-system with shunt reactors R/(Ω/km)L/(mH/km)C/(μF/km)正序0.07580.8390.01397零序0.15422.6450.00930 利用该模型分别对伴随强拍频振荡和几种弱拍频振荡的瞬时性故障进行仿真。超/特高压潜供电弧熄灭时间90%概率值小于0.2s[17],取熄弧后时间窗为0.2ms的数据验证方法的有效性,考虑到现场录波的噪声干扰,采用人工染噪方式加入噪声,直接对含噪信号进行分析,将瞬时性故障区分出来。 5.2 故障仿真 5.2.1 强拍频振荡 设置并联补偿度k=80%,电源相角差θ=30°,此时自振分量的频率低于45Hz,与工频分量的频率差较大,能够观察到强拍频振荡,电抗器电流量如图3所示。 图3 强拍频振荡Fig.3 Strong beat-frequency phenomenon 其中,自振分量的能量强度一定程度上受到故障点位置和过渡电阻的影响,从而削弱拍频振荡的显著程度。其影响特性如图4所示,图中P为故障点到M端的距离占线路全长的比值,拍频强度以P=20%、Rg=0时为基准。 图4 拍频振荡强度特性Fig.4 Beat-frequency strength characteristic 限于篇幅,取此时拍频振荡强度较弱的情况(P=80%,Rg=500Ω)进行故障辨识。为了量化本文检测方法的性能,在不同噪声背景下,对强拍频振荡和永久性故障下电流量分别求解FrFT域扩展Hurst指数,然后与传统时域检测方法进行对比,差异提升效果如表2所示。 表2 FrFT域Hurst指数对强拍频检测效果Tab.2 Detection results of strong beat-frequency 可见,瞬时性故障下,本文方法具有良好的噪声免疫能力,且不受故障点位置和过渡电阻的影响,在不同噪声背景下均能直接对含噪信号进行分析,有效准确地辨识故障性质。 5.2.2 弱拍频振荡 分别对下面三种弱拍频振荡进行仿真:①设置并联补偿度k=90%,两侧电源相角差θ=30°,电抗器阻抗角ψ=89.9°;②设置并联补偿度k=70%,两侧电源相角差θ=0°,电抗器阻抗角ψ=89.9°;③设置设置并联补偿度k=85%,两侧电源相角差θ=0°,电抗器阻抗角ψ=82°。瞬时故障下电抗器电流如图5所示。 图5 弱拍频振荡Fig.5 Weak beat-frequency phenomenon 可以直观地看出,仿真结果与理论分析基本一致,在不完全满足拍频振荡起振条件时,瞬时故障下的电抗器电流量并不能观察到强拍频振荡,给故障性质识别带来困难。同样地,在不同噪声背景下,利用本文检测方法对三种种弱拍频振荡与各自对应的永久故障下电流量进行检测,结果如表3~表5所示。 表3 FrFT域Hurst指数对弱拍频1检测效果Tab.3 Detection results of weak beat-frequency 1 表4 FrFT域Hurst指数对弱拍频2检测效果Tab.4 Detection results of weak beat-frequency 2 表5 FrFT域Hurst指数对弱拍频3检测效果Tab.5 Detection results of weak beat-frequency 3 仿真结果表明,FrFT域扩展Hurst指数效果更明显,比利用同数据时域检测结果提升200%以上,而且各种情况下均能灵敏地捕捉到拍频特征。当输电系统发生故障且信噪比较高时,时域分形参数能在一定程度上描述永久性故障和瞬时性故障电气量的非线性特征差异,但当信噪比较低时,随机噪声的能量较大,电气量的非线性差异特别是微弱差异容易被噪声“淹没”。而本文方法凭借对非线性信号优异的分析能力,即使线路处于极端恶劣的故障状态下仍可清晰地表达出故障信号间的非线性特征差异,弥补了传统判据的不足,完善了超高压线路的自适应重合闸技术。 输电系统在瞬时故障下发生的弱拍频振荡造成了拍频判据故障识别盲区。本文提出了一种基于FrFT域扩展Hurst指数的全拍频检测方法。该方法在伴随强拍频振荡的瞬时故障下,能够周全地考虑到一定强度噪声对检测方法的影响;当瞬时故障伴随弱拍频振荡时,该方法能够快速准确地捕捉到拍频特征的存在。仿真结果表明,该方法适用于单相自适应重合闸故障分析,克服了传统线性判据难以处理非线性、非平稳信号的缺陷,具有优秀的噪声免疫能力,消除了拍频判据识别盲区,为区分故障性质提供依据,并且可为实现基于拍频特征的故障识别提供一种新的思路。 [1] 李斌, 李永丽, 盛鹍 (Li Bin, Li Yongli, Sheng Juan). 带并联电抗器的超高压输电线单相自适应重合闸的研究(The study on single-pole adaptive reclosure of EHV transmission lines with shunt reactor) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2004, 24(5): 52-56. [2] 索南加乐, 孙丹丹, 付伟, 等 (Suonan Jiale, Sun Dandan, Fu Wei, et al.). 带并联电抗器输电线路单相自动重合闸永久故障的识别原理研究 (Identification of permanent fault for single-phase auto-reclosure on transmission lines with shunt reactor) [J]. 中国电机工程学报 (Proceedings of the CSEE), 2006, 26(11): 75-81. [3] 李博通, 李永丽 (Li Botong, Li Yongli). 带并联电抗器的超高压输电线路自适应重合闸新判据 (A new critierion for adaptive single pole auto-reclosure of EHV transmission lines with shunt reactor compensation) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2009, 33(23): 48-54. [4] 李斌, 李永丽, 曾治安, 等 (Li Bin, Li Yongli, Zeng Zhi’an, et al.). 基于电压谐波信号分析的单相自适应重合闸(Study on single-pole adaptive reclosure based on analysis of voltage harmonic signal) [J]. 电网技术(Power System Technology), 2002, 26(10): 53-57. [5] 林达, 王庆庆, 王慧芳, 等(Lin Da, Wang Qingqing, Wang Huifang, et al.). 带并联电抗器同杆双回线自适应重合闸方案 (Adaptive reclosure scheme for parallel lines with shunt reactor) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2015, 39(6): 101-106. [6] 姜艳茹, 费玉琢, 李子星, 等 (Jiang Yanru, Fei Yuzhuo, Li Zixing, et al.). 基于样本熵理论的输电线路单项自适应重合闸研究 (Study about single-pole adaptive reclosure of transmission based on sample entropy) [J]. 电测与仪表 (Electrical Measurement & Instrumentation), 2012, 49(3): 41-45. [7] 郑涛, 刘敏, 董淑惠 (Zheng Tao, Liu Min, Dong Shuhui). 基于故障相并联补偿电流变化特征的单相自适应重合闸 (Single-phase adaptive reclosure based on variation trend of decaying components of fault phase shunt reactor currents) [J]. 电力系统自动化 (Automation of Electric Power Systems), 2011, 35(10): 74-78. [8] 何柏娜, 赵云伟, 林鹤云 (He Baina, Zhao Yunwei, Lin Heyun). 带并联电抗器的交流特高压输电线路单相自适应重合闸故障识别方法 (Fault identification method for single-phase adaptive reclosure on UHV AC transmission lines with shunt reactors) [J]. 高压电器(High Voltage Apparatus), 2013, 49(12): 13-18. [9] 邵文权, 南树功, 章霄微, 等 (Shao Wenquan, Nan Shugong, Zhang Xiaowei, et al.). 带并补电抗器超/特高压输电线路单相瞬时故障拍频特性研究 (Beat-frequency characteristics for single-phase transient fault of EHV/UHV transmission line with shunt reactor) [J]. 电力自动化设备(Electric Power Automation Equipment), 2014, 34(5): 72-78. [10] 杨光, 李绍滨, 姜义成 (Yang Guang, Li Shaobin, Jiang Yicheng). 基于分数阶傅里叶变换的星载SAR信号参数实时估计(Real time estimation of space-borne SRA signal parameter with FrFT) [J]. 系统工程与电子技术 (Systems Engineering and Electronic), 2010, 32(8): 1649-1651. [11] 朱建军, 魏玉阔, 杜伟东, 等 (Zhu Jianjun, Wei Yukuo, Du Weidong, et al.). 基于分数阶傅里叶变换的Chirp浅剖精细探测方法 (Chirp sub-bottom profiling detailed detection method based on fractional Fourier transform) [J]. 电子与信息学报(Journal of Electronics & Information Technology), 2015, 37(1): 103-109. [12] 梅检民, 李枫, 杨青乐, 等 (Mei Jianmin, Li Feng, Yang Qingle, et al.). 基于最佳阶次FrFT的阶比分量提取(Order component extraction based on best order fractional Fourier transform) [J]. 汽车工程(Automotive Engineering), 2014, 36(12): 1494-1497. [13] 曲强, 金明录 (Qu Qiang, Jin Minglu). 基于自适应分数阶傅里叶变换的线性调频信号检测及参数估计(Adaptive fractional Fourier transform based chirp signal detection and parameter estimation) [J]. 电子与信息学报(Journal of Electronics & Information Technology), 2009, 31(12): 2937-2940. [14] 石敦义, 缪希仁, 郭谋发 (Shi Dunyi, Miao xiren, Guo Moufa). 基于分形理论的低压断路器三相合闸同期性振动信号特征分析 (Vibration signal feature analysis of switching synchronization for low voltage circuit breaker based on fractal theory) [J]. 电工电能新技术 (Advanced Technology of Electrical Engineering and Energy), 2014, 33(5): 44-50. [15] 宋平岗, 周军 (Song Pinggang, Zhou Jun). 基于形态学广义分形维数的电力电子电路故障诊断 (Fault diagnosis of power electronic circuits based on mathematical morphology based generalized fractal dimensions) [J]. 电工电能新技术(Advanced Technology of Electrical Engineering and Energy), 2014, 33(12): 53-59. [16] 行鸿彦, 张强, 徐伟 (Xing Hongyan, Zhang Qiang, Xu Wei). 海杂波FRFT域的分形特征分析及小目标检测方法 (Fractal property of sea clutter FRFT spectrum for small target detection) [J]. 物理学报 (Acta Physica Sinica), 2015, 64(11): 110502. [17] 韩彬, 林集明, 班连庚, 等 (Han bin, Lin Jiming, Ban Liangeng, et al.). 1000kV特高压交流试验示范工程单相重合闸研究 (Study on single-phase reclosing issues for 1000kV UHVAC transmission pilot project) [J]. 电网技术 (Power System Technology), 2009, 33(16): 20-23. Completely beat-frequency detection method for transient fault in EHV/UHV transmission lines based on extended Hurst index in adaptive FrFT domain ZHANG Yu-hui, WU Jia-ming, WU Dong-bin, WANG Jie-yan (School of Electrical Engineering, Northeast Dianli University, Jilin 132012, China) That transient fault which has a threat on EHV transmission lines security frequently accompanied by strong beat-frequency is an universal viewpoint, but weak beat-frequency phenomenon has been discovered already by analysis that oscillatory condition may cause misjudgment of criterion which could cause serious consequences in power network. This paper proposes a completely beat-frequency detection method which could be used to extract nonlinear characteristics from fault current recorded in shunt reactor to solve this indicated problem. Specifically, fixing best fractional Fourier transform domain (FrFT) firstly, in which nonlinear characteristics can be enlarged far better, then calculating the extended Hurst index of current waveform in that domain as a nonlinear quantitative criterion for distinguishing transient fault from permanent fault. This method has excellent immunity to noises, and can obtain reliable detection result fleetly no matter whether strong or weak beat-frequency occurs in fault waveform after single-phase transient fault. The method has been proved to be effective and reliable by numerous EMPT simulations. FrFT; extended Hurst index; beat-frequency; nonlinearity-amplifier 2015-07-20 张宇辉(1962-), 男, 吉林籍, 副教授, 从事自动控制理论、 信号处理在电力系统中的教学与应用研究工作; 吴家明(1993-), 男, 江西籍, 硕士研究生, 主要研究方向为电力系统信号模态识别。 TM77 A 1003-3076(2016)05-0013-06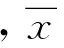
5 仿真分析


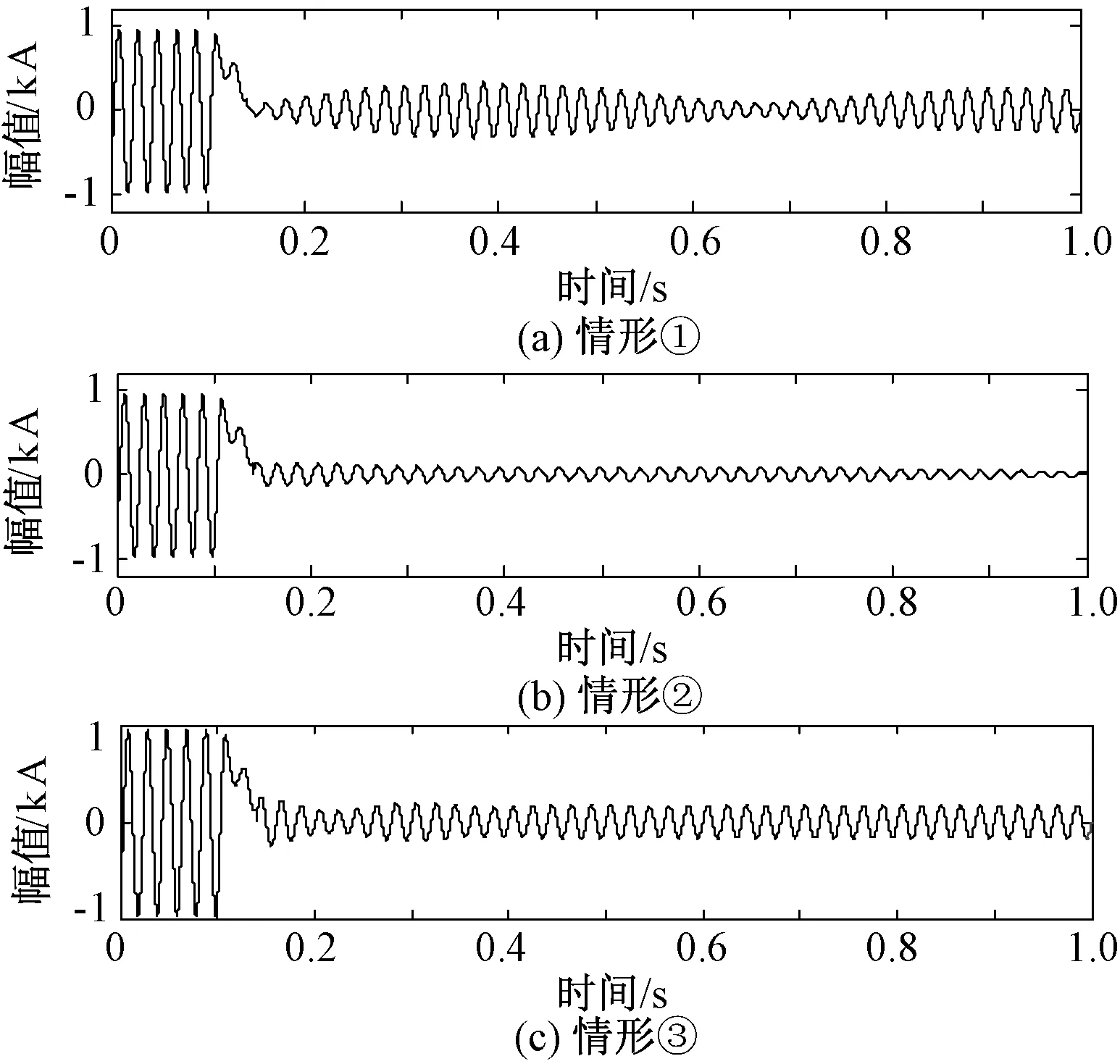
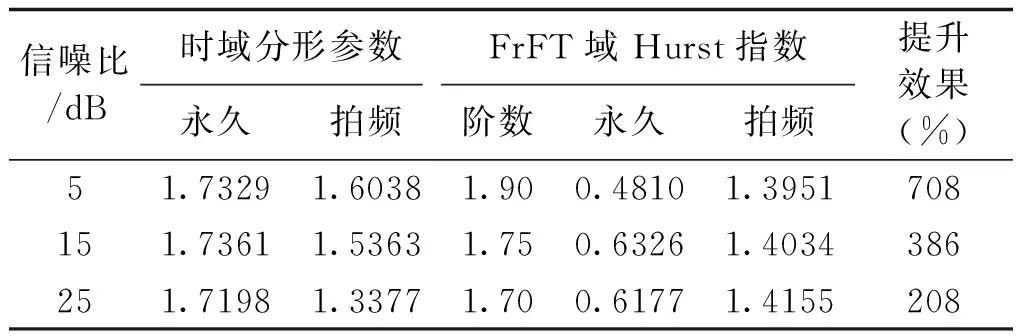
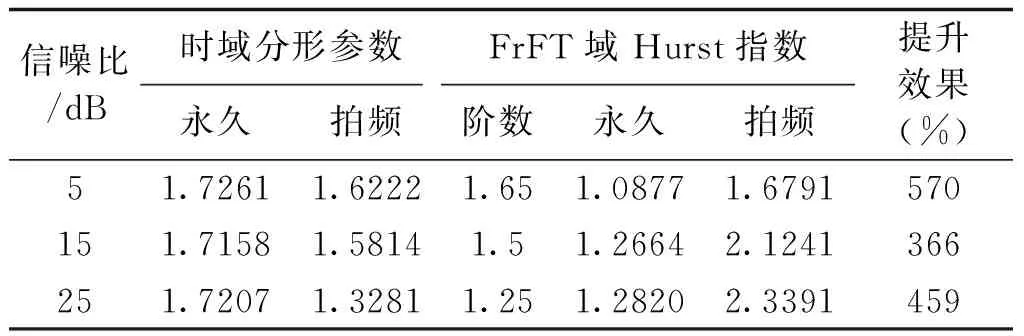
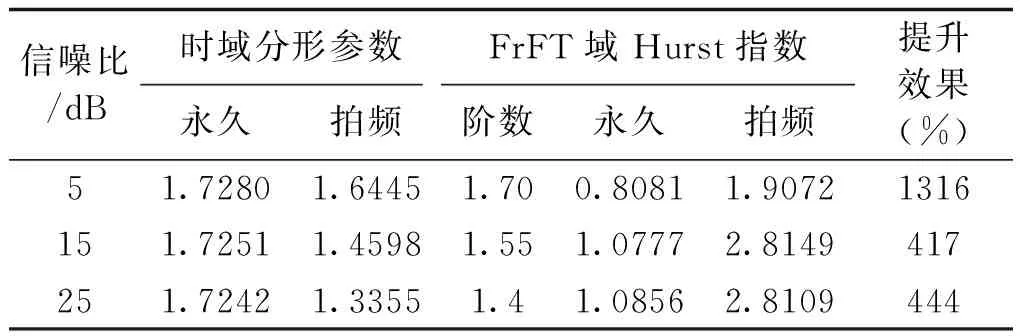
6 结论

