世间最神秘的三个数字（十三）

刘玮

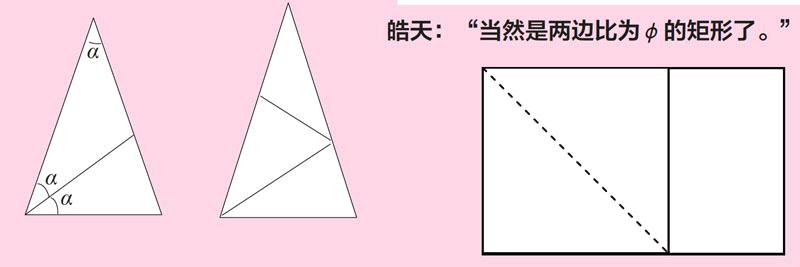
说话间，皓天用手中的纸剪出了两个黄金三角形：“下一代的黄金三角形在哪儿？”

“在长边上找到黄金分割点，并与它的对角相连看看，它将原来的黄金三角形分成了两个小的黄金三角形，一个是锐角黄金三角形，另一个是钝角黄金三角形。”

“等等——这里有玄机！”皓天灵光闪现，“子代与父代都是黄金三角形，是相似的，设锐角为α，分割后由相似可看出其底角一定为2α，那么这个α就能求出来了，5α=180°，α=36°，底角就是72°。同时可以看出：钝角黄金三角形的顶角是180°-2α=108°。”

“这个繁殖过程也可以用折叠法了！”鹏飞提示道。

“对，将底角对折一次，出现两个二代黄金三角形，折一次后不打开，沿小三角形的底线再折一次，第三代的小黄金三角形也出来了。如此下去，就可以繁殖出一系列的黄金三角形。”

鹏飞觉得讨论可以再深入下去了：“最美矩形应该是什么样子的呢？”

皓天：“当然是两边比为φ的矩形了。”

“能用折叠法繁衍出下一代的黄金矩形吗？”

“可以啊，对折一角，折出一个正方形，余下的还是一个黄金矩形。依次折出正方形，就可无限繁衍出越来越小的黄金矩形，最终趋向于一个点。”

鹏飞：“是的，这个点被称为‘上帝之眼，仿佛正是从这里繁衍出了这些无数的正方形。更奇妙的是，如果过这些正方形对角画曲线，就形成了对数螺线的轮廓。”

“对数螺线的方程是什么？”

“用极坐标方程表示：r = aeθ 。”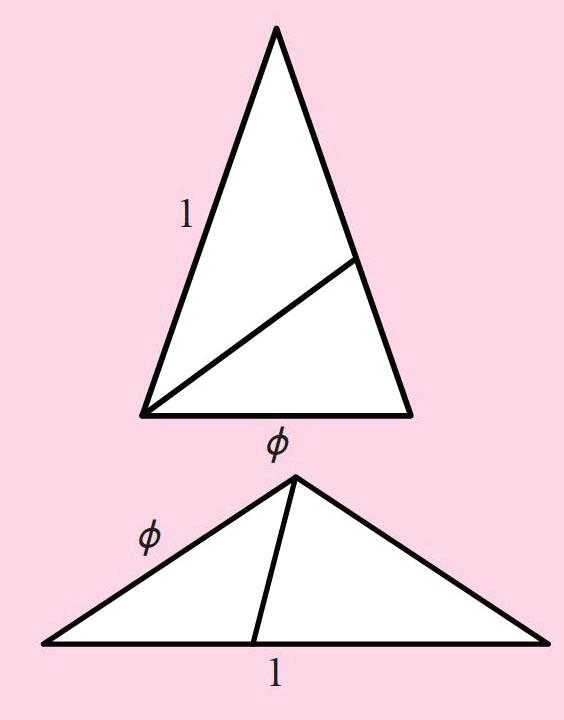

“原来黄金数φ与e还有这种渊源呢！”皓天不禁喃喃自语道，“黄金三角形、黄金四角形，前面分割的线段也可以说是二角形，应当还有黄金五角形、六角形……这是平面的，立体的就应该有黄金四面体、黄金长方体……四维空间的是不是还有许多黄金超体啊？”

鹏飞惊诧了：“我的知识也有限，只知道金字塔是黄金四面体，五角星是当年毕达哥拉斯学派的标志，里面有好多黄金比，黄金长方体的长宽高之比为1∶0.618∶0.382。另外，曲线家族里也有黄金比，比如黄金椭圆、对数螺线等，至于其他的，我也不了解了。”

“它们的共同特点是具有黄金比，一定也都可以通过折叠法繁衍出无数个小的自相似图形来。”皓天又陷入了沉思中。