双模行星耦合式油电混合动力系统的参数优化

赵升吨，杨雪松，杨红伟，杨元元

（西安交通大学机械工程学院，陕西 西安 710049）

双模行星耦合式油电混合动力系统的参数优化

赵升吨，杨雪松，杨红伟，杨元元

（西安交通大学机械工程学院，陕西 西安 710049）

双模行星耦合式油电混合动力系统由两组或三组行星排构成，通过对离合器的控制实现输入分流式和复合分流式的切换,使得系统在全速比范围内效率较优。文章分析了现有不同类型功率分流式混合动力装置的输出特性与系统匹配参数关系，论证双模行星耦合式混合动力系统的优越性，提出了两种易于结构化实现的系统构型，以杠杆法为基础、以系统效率为优化目标进行了参数化设计。

双模；混合动力；功率分流；行星耦合

CLC NO.:U462.1 Document Code: A Article ID: 1671-7988 (2016)07-27-05

前言

汽油内燃机与电动机混合驱动的汽车，即油电复合汽车作为汽柴油车向电动车转化的过渡产品，在接下来的一段时间内会在市场上占领很大的份额，并且向多元化发展。行星耦合式功率分流无级传动系统是指利用行星机构将发动机所传递出的功率分流为机械和电气两条路径进行传递，并最终汇流驱动汽车的变速装置。该系统综合了无级变速和电动化这两大技术，能实现电子无级变速的功能，因此也有学者[1]将其称为e-CVT结构或EVT结构[2]。功率分流式混合动力系统实现了发动机和负载的解耦，既保证发动机工作在效率较高的区域，又充分利用机械功率流传递效率、可靠性高的优点，可大幅提高车辆的燃油经济性和动力性能[3]。目前较成功的混合动力汽车包括日本丰田公司的“Prius”[4]和美国通用公司的产品“Allison”[5]等，它们的变速箱均采用了基于行星耦合装置的功率分流式混合动力系统。

针对混合动力车辆传动系统的方案设计与输入输出特性分析，国内外学者开展了广泛的研究。文献[1]综述了现有混合动力车辆技术，分析了不同类型传动结构的特点及电机工作特性；文献[6-7]对两自由度行星传动系统进行了运动学及动力学分析；文献[8-9]基于以Prius为代表的输入分流式系统，对系统的工作原理进行了介绍，并对动力系进行了分析设计；文献[10-11]分别对输入式和复合式功率分流混合动力系统进行了参数化研究；文献[12-13]对混合动力车辆的控制方法进行了研究，对车辆行驶中变速箱不同工作模式间的切换控制进行了优化；文献[14]提出了一种方法对双模混合动力系统的构型进行分析。但综上所述，目前关于功率分流式混合动力传动系统的研究多局限于输入分流式或复合分流式等单一模式，对于集成了这两种模式的双模混合动力传动系统中的行星齿轮机构的设计研究还尚少，尤其在进行构型设计时很少考虑其结构可行性。因此，有必要通过分析和参数化设计确定一种结构可行的较优方案，并对设计结果进行检验评估。

本文对功率分流式双模混合动力系统的构型设计进行了深入的研究，进行了基于杠杆法的构型设计及其扩展演化，并进行了两种结构方案的参数化设计；然后创造性地提出以全速比范围电功率特征值作为优化目标以确定第三排行星传动机构特征参数的方法，并用此方法对提出的两种方案进行了优选。

1、行星耦合式功率分流系统

1.1 功率分流系统的构型分析

1.1.1 杠杆法

前文中已提到，功率分流系统中用到的行星轮系有两个自由度，这使得如果直接在原有模型上进行转速转矩分析时会有较大困难。为此，H.L.Benrord和M.B.Leising在文献[15]中提出了用杠杆模拟行星轮系的分析方法。杠杆模拟法是将轮系中的各构件的角速度模拟为一特定杠杆上不同点对应的速度，将轮系中各构件受到的扭矩模拟为杠杆上对应点受到的力[16]。

1.1.2 机械点

功率分流式混合动力系统中发动机输出的功率经行星耦合机构后分流为机械功率和电功率两条路径进行传递，在此过程中实现电子无级变速功能以及将发动机工作点维持在最优工作曲线附近。当系统不需要外部提供电能即电池功率为零时，会存在某一传动比值处发动机功率全部以机械功率进行传递，即系统中无电功率的传输，此时，两电机功率均为零。反应到动力系统构型上，某一电机的转速为零，另一电机的转矩为零。这个特定的传动比值被称为机械点。输入分流模式中由于电机2与输出相连，正常工作时转速不能为零，而输出分流模式中由于电机1与发动机相连，转速不能为零，故这两种模式均只有一个机械点；复合分流模式由于采用双行星排，系统具有两个机械点。

1.1.3 复合分流模式的杠杆模型

复合分流式结构中的双行星排共有四个相互独立的接点，将其体现在杠杆模型中即为四节点杆模型，发动机、电机1、电机2和输出端与四节点连接组成不同的构型，如图1 （1）所示。在利用四节点模型对结构中各构件中的转速进行分析时，可根据节点处连线的长度及位置关系来判断该点的转速大小及方向，如图1（2）所示。 当系统工作在两机械点时，其各构件转速如图1（3）（4）所示。从图中可看出，在机械点1，电机1转速为零，发动机与输出转速方向相反；在机械点2，电机2转速为零，发动机与输出转速方向相同。车辆实际工作过程中，要求在正向行进时，发动机始终与输出转向相同，故该结构不合理。

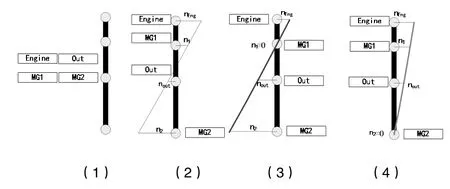
图1 四节点杆模型及节点转速图

对四节点杆模型分析可得知，若要系统具有两个机械点，且在两机械点处发动机转速及输出转速均为正值，发动机和输出端必须连接在相邻两节点。基于此原则，共可确定出如图2中的三种合理的构型。

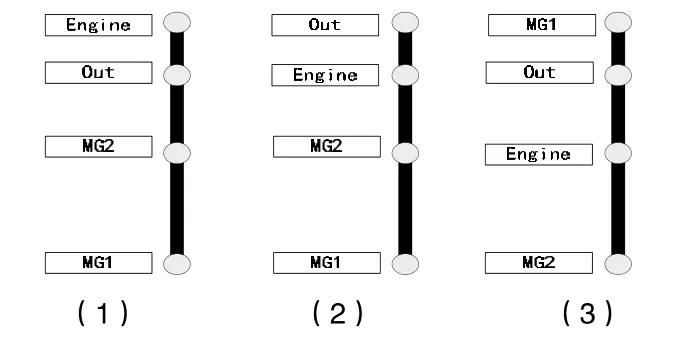
图2 三种合理的四节点杆模型

复合分流式系统的结构有上百种可能性，对图2中三种模型就行分析，可以发现只有图2（3）中所示的结构的两个机械点分布在γ=1两侧。本文在进行设计时考虑的系统全速比范围内的效率最优，因此选择第三种四节点杆模型进行拆分。在进行不同构型拆分时，方法基本一致，每个四节点杆模型可分解成四种三节点杆模型，将其进行两两组合即可得到不同的结构。考虑到实际连接结构的复杂程度及工艺性，将其拆分组合成如图3所示的两种结构进行接下来的参数化研究。

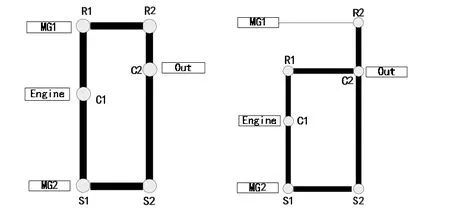
图3 两种复合分流结构构型

1.2 双模混合动力系统

行星耦合功率分流式混合动力系统的传动比在机械点附近效率较高，在偏离机械点时效率会下降较快。复合分流式系统具有两个机械点，在进行系统效率优化时，机械点的取值就显得尤为重要。若两点相离很近，则在两机械点外系统效率很低；若两机械点相聚较远，则在两机械点间系统效率会达到一个相对较低的值。汽车变速箱的常用传动比都在0.6~2.2或更大范围内，这就使得很多时候具有两机械点的复合分流系统不能最大程度上满足系统综合效率最低的要求，双模混合动力系统就是在这种情况下被提出的。功率分流式双模混合动力系统由两个或三个行星排组合，通过离合器的不同组合来实现输入分流式和复合分流式的切换。若想系统具有三个机械点，在更宽的速比范围内具有较高效率，需采用三个行星排的结构，如图4所示。当系统工作在输入分流模式时，第一离合器断开，第二离合器结合；当系统工作在复合分流模式时，第一离合器结合，第二离合器断开。

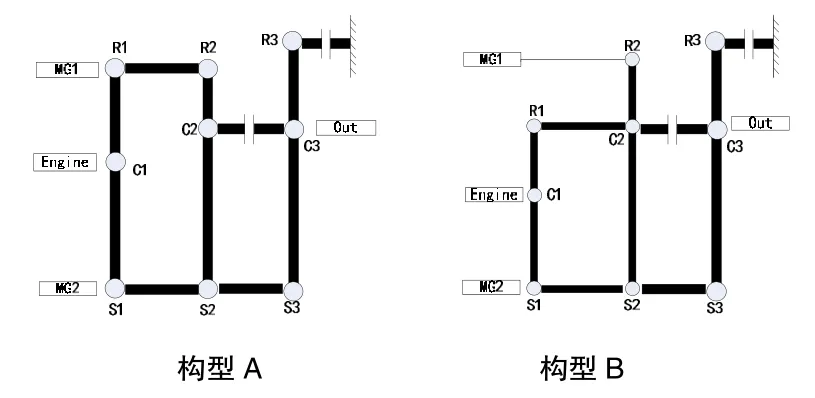
图4 两种功率分流双模式系统构型

2、系统的参数化设计及效率优化

2.1 复合分流系统的参数化计算

在对复合分流式混合动力系统进行参数化设计的过程中，需要考虑到车辆对变速箱的输出特性要求以及系统中各动力原件的固有特性限制。系统中发动机被控制在其最优工作曲线附近，因此主要需考虑的是两个电机的输出特性是否能满足系统要求，下面对电机的转速转矩进行分析。

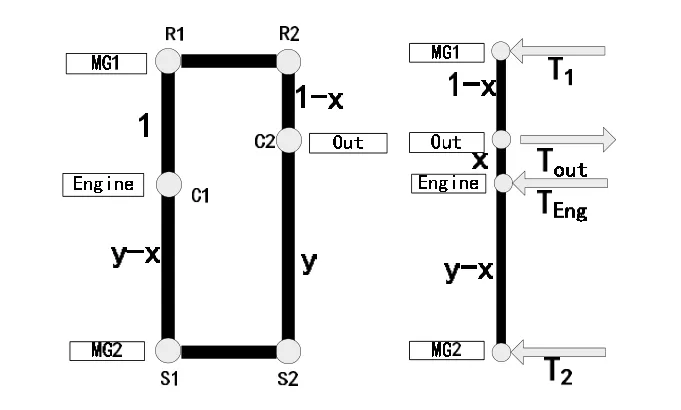
图5 构型A分析模型

构型A的分析模型如图5所示，对其利用杠杆法分析，并对其杆长度进行参数化假设，得到其四节点转速转矩的关系表达式：

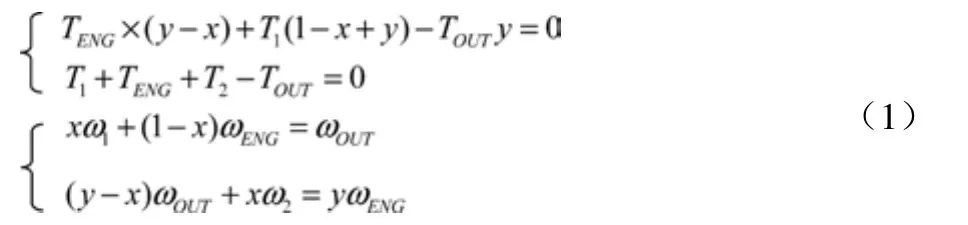
首先可求出构型A的两机械点的表达式：

当ω1=0时，代入上式，γ1=ωEng/ωout=(y-x)/y；

当ω2=0时，代入上式，γ2=ωEng/ωout=1/(1-x)；

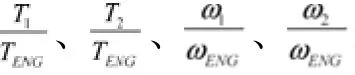
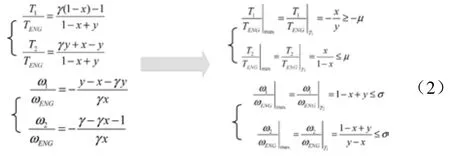
根据上式求得x，y取值范围，并在范围内选择其设计值，此处我们选择x=0.25，y=2.25。则，γ1=8/9，γ2=4/3。

对构型B的杠杆模型进行转速转矩分析，如图6所示：可得到下式：

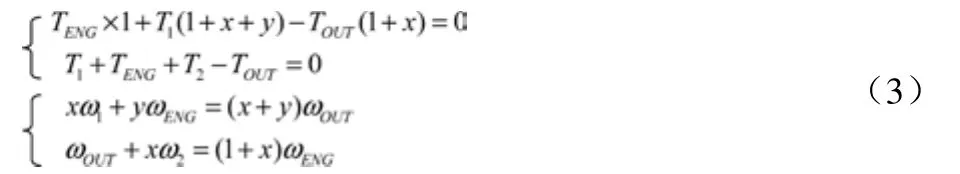
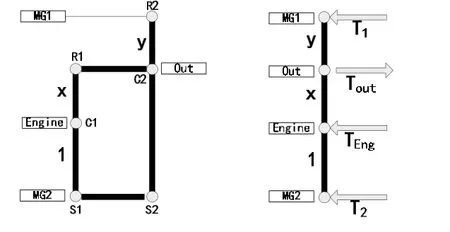
图6 构型B分析模型

同样，我们可求出构型B的两机械点表达式：γ1= (x+y)/y，γ2= 1/(1+x)，再根据两电机的转速转矩约束求其x，y的取值范围：

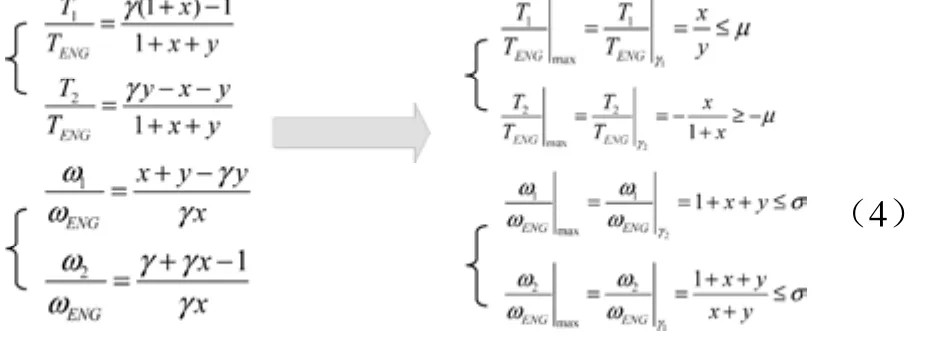
在此范围内我们选择x=1/3，y=2/3这一组合值，可求得两机械点取值，则，γ1=1.5，γ2=0.75。并在接下来对设计结果进行检验。

2.2 混合动力系统的效率分析

从功率分流式混合动力系统的定义中我们可以看出，在系统内有机械能和电能两种能量传递途径。在上文的分析中我们没有考虑电功率在机械能-电能-机械能间转化时的效率问题，其实无论是MG1还是MG2在发电模式还是电动模式工作时都存在能量损失。因此，我们在要求系统完成发动机工作在最优工作曲线以及实现电子变速功能的同时，希望系统的能量损失最小，即希望电功率在总传递功率中所占的比例最小。此处，我们引入电功率比例这一值作为评价指标，定义：

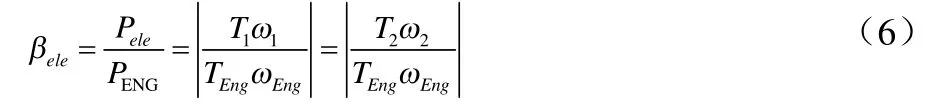
下面我们分别对构型A和构型B的电功率比例值进行分析。

联立（2）（6）两式，可得构型A的电功率比例表达式：

作出图像对两构型的电功率比例值进行比较，如图7所示。

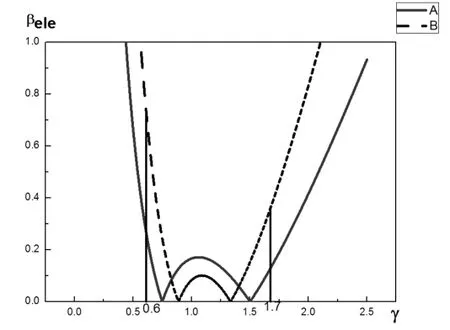
图7 A、B构型的电功率

从图中可以看出，在两机械点之间，构型B的电功率比例值较小，但在两机械点之外，该比例值急剧上升。为了更加直观的对两构型的效率进行比较，引入电功率特征值Sβ，并定义：

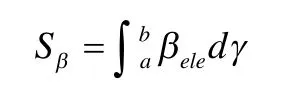
其中a，b为需考察的传动比范围的上下限。本文在设计时选择的原型车变速箱常用传动比范围为0.6~2.2，此处考虑的是双模混合动力的复合分流部分，主要覆盖了传动比范围内较小的两个机械点，故选择γ=0.6和γ=1.7作为电功率特征值计算时的上下限，经过计算：

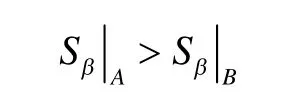
因此，从全速比范围内系统效率较优的角度考虑，选择构型B作为本文所设计的双模混合动力系统的复合分流部分。

2.3 第三排行星轮的设计

本文设计的是输入分流和复合分流组合的双模式混合动力系统，输入分流适宜工作在低速大传动比的场合。此节的任务主要是确定合理的第三排行星结构特征参数，使得混合动力系统的三个机械点分布合理，系统整体效率最优化，并确定系统在两模式间的切换点。构型B的双模式工作分析结构如图8所示。

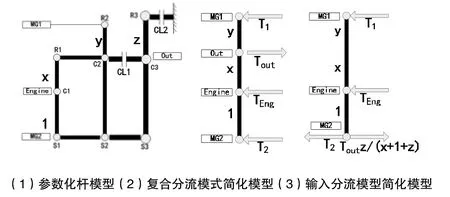
图8 双模式混合动力系统分析模型

列出输入分流模式下系统的转速转矩关系式：

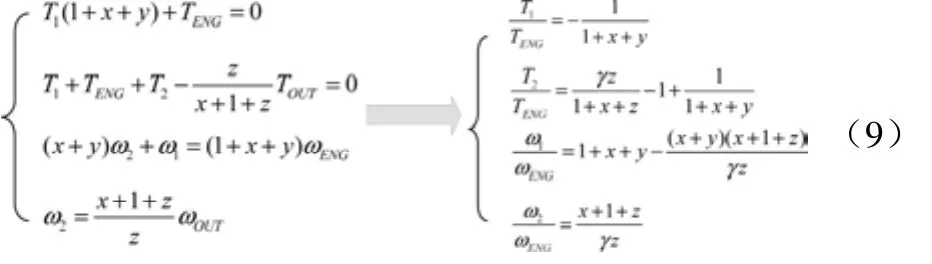
输入分流模式时，只有电机MG1转速可为0，据此可求出机械点3，当ω1=0时，代入上式：

联立，可解得：

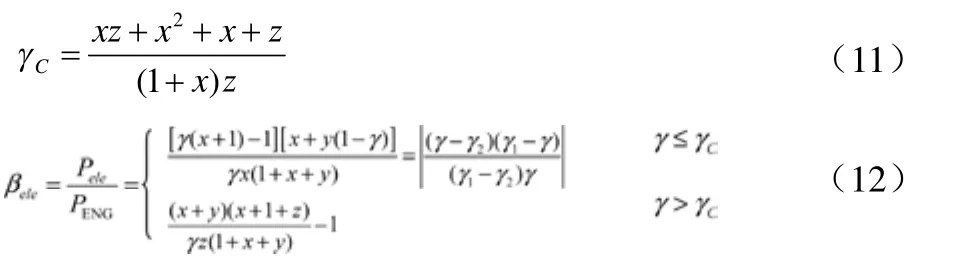
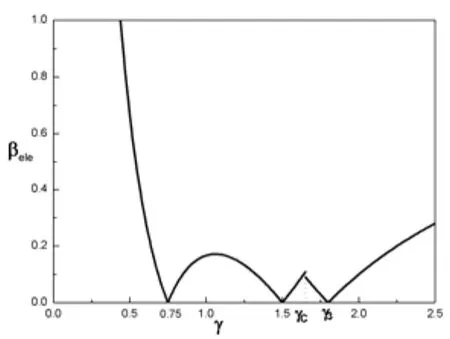
图9 双模混合动力系统电功率比例图

联立（4）（8）（9）（11），可求得双模混合动力系统在全速比范围内的电功率比例值函数，将x=1/3，y=2/3代入，作出函数图像如图9所示。

在对第三排行星结构进行参数化设计时，同样引入电功率特征值Sβ，确定变速箱的常用传动比区间0.6和2.2。求出特征值Sβ关于参数z的表达式，并作出其函数图像，如图10所示。

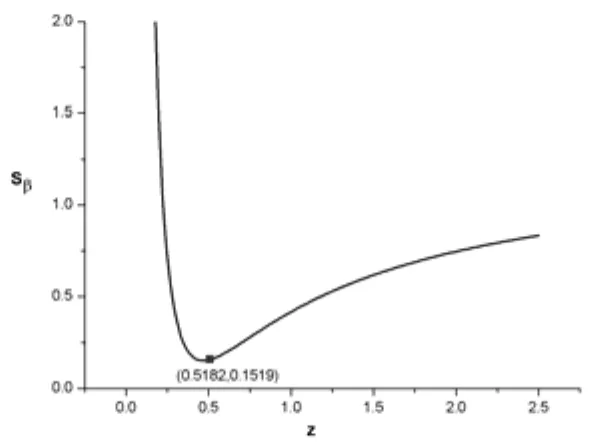
图10 系统Sβ-z函数图像

通过计算可得出，使电功率特征值Sβ取得最小值的z=0.5182，即第三排行星结构的特征参数k=(1+x)/z=2.6时，系统整体效率最优。

3、结论

本文设计了一种基于行星耦合装置的混联式混合动力系统，具有输入分流和复合分流两种工作模式。车辆运行时该系统可根据车速及扭矩需求进行模式切换，保证在全速比范围内混合动力系统都具有很高的效率。在进行系统的参数化设计时，采用电功率特征值作为系统效率的评价指标，并定义电功率特征值为电功率比例值在全速比范围内的积分，具体体现为：

（1）进行前两组行星排参数设计时，对提出的两种构型在复合分流模式下的电功率特征值进行比较，以确定较优结构方案；

（2）第三组行星排设计过程中，以全速比范围内电功率特征值作为优化目标，行星排特征参数作为变量进行分析，计算出最优参数取值。

[1] Miller,J.M., Hybrid electric vehicle propulsion system architectures of the e-CVT type. IEEE Transactions on Power Electronics, 2006. 21(3): p. 756-767.

[2] 薛天扬,彭增雄.双模式功率分流混合动力车辆功率优化与仿真.机械设计与制造, 2014(7): p. 8-11.

[3] 韩立金, 李宏才, and 韩全福, 功率分流混合动力车辆模糊控制策略设计与仿真.机械设计与制造, 2011(7): p. 4-6.

[4] Prokhorov, D. Toyota Prius HEV neurocontrol. in Neural Networks, 2007. IJCNN 2007. International Joint Conference on. 2007.

[5] Miller, J.M., et al. Ultracapacitor Plus Battery Energy Storage System Sizing Methodology for HEV Power Split Electronic CVT's. in Industrial Electronics, 2005. ISIE 2005. Proceedings of the IEEE International Symposium on. 2005.

[6] pennestri, E. and p.p. valentini, 两自由度周转轮系机械效率分析公式的评议.传动技术, 2004. 18(1): p. 34-40.

[7] Huang, K.J. and T.S. Liu, DYNAMIC ANALYSIS OF A SPUR GEAR BY THE DYNAMIC STIFFNESS METHOD. Journal of Sound & Vibration, 2000. 234(2): p. 311-329.

[8] 张金柱, 丰田第二代混合动力系统(THSⅡ).内燃机, 2005(3): p. 6-9.

[9] 韩立金, et al., 功率分流混合动力汽车参数匹配与优化研究.汽车工程, 2014(8): p. 904-910.

[10] 项昌乐, et al., 混联混合动力车辆功率分流耦合机构特性分析.汽车工程, 2010. 32(3): p. 183-187.

[11] 杜爱民,刘开圣,朱忠攀等.单模复合功率分流混合动力系统结构优化[J].中国机械工程,2015,(21):2976-2981.DOI:10.3969/ j.issn. 1004-132X.2015.21.023.

[12] 薛天扬,彭增雄.双模式功率分流混合动力车辆功率优化与仿真.机械设计与制造, 2014(7): p. 8-11.

[13] Ahn, K., Optimal Operation of the Power-Split Hybrid Electric Vehicle Powertrain. Journal of Research of the National Institute of Standards & Technology, 1951. 58(5): p. 789-800.

[14] 王伟华, et al..双模功率分流式混合动力系统构型分析.汽车工程, 2015(6): p. 648-654.

[15] Benford, H. L., & Leising, M. B. (1981). The lever analogy: A new tool in transmission analysis. SAE Technical Papers, doi:10.4271/ 810102

[16] 刘钊, 赵世琴, and 黄宗益, 用杠杆模拟法建立行星变速器动力学模型.汽车工程.2000. 22(4): p. 274-277.

Parameter optimization of a two mode planetary coupled hybrid electric power system

Zhao Shengdun, Yang Xuesong, Yang Hongwei, Yang Yuanyuan
( School of Mechanical Engineering, Xi'an Jiaotong University, Shaanxi Xi'an 710049 )

Dual mode planetary coupling type oil electricity hybrid power system is made up of two or three groups of planetary rows, it can switch between input split type and compound split type through controlling clutches, which makes the system efficiency optimalin full speed range. This paper analyzes the output characteristics and system parameters matching of existing different types of power-split hybrid power devices, demonstrates the superiority of dual-mode planetary coupling hybrid system, designs two structure which is easy to realize the configuration, using the lever method as foundation, using the system efficiency as the target to optimizethe parametric design.

dual-mode; hybrid electric vehicles; power split; planetary coupling

U462.1

A

1671-7988(2016)07-27-05

赵升吨，西安交通大学教授，博士生导师，研究方向为汽车节能机电一体化设备开发。

国家自然科学基金重点项目（编号：51335009）。

10.16638/j.cnki.1671-7988.2016.07.009