基于Chua电路的一个超混沌系统的控制同步

赵军产,魏耀斌,谢小良,罗智明

(1.湖南商学院 数学与统计学院,长沙 410205; 2.武汉纺织大学 数学与计算机学院,武汉 430072)



基于Chua电路的一个超混沌系统的控制同步

赵军产1,魏耀斌2,谢小良1,罗智明1

(1.湖南商学院 数学与统计学院,长沙 410205; 2.武汉纺织大学 数学与计算机学院,武汉 430072)

摘 要:Chua电路具有广泛的应用价值,受到越来越多的研究者的关注.借助于最新提出的忆阻器电路元件,在Chua系统的基础上构造了一个新的超混沌系统.通过PC控制和线性反馈方法,分析了两个线性耦合的超混沌系统的同步,数值仿真也验证了理论分析的有效性.

关键词:Chua电路; 超混沌系统; 同步

引言

1971年,著名的电路专家蔡少棠教授提出了一种新型两端口无源器件—忆阻器(memristor),并于2008年由美国惠普(HP)公司研制成功.该器件具有的记忆和非线性功能,使得忆阻器在人工智能、超高密度信息存储、可编程电路等新兴电子信息技术领域中有着潜在的重要应用.因此被认为是除电阻、电容、电感之外的第四种基本电路元件.

Chua电路系统[1,2]可用三个常微分方程来描述,该系统可由传统的电路元件实现,在此基础上可生成多涡卷混沌系统,目前已广泛应用于电路、液体搅拌等领域.传统的Chua电路系统仅有一个Lyapunov指数大于零,是一个典型的混沌系统.借助于忆阻器新型的电路元件,杨芳艳[3]等人提出了一个新型的超混沌系统,该系统可以通过忆阻器代替传统的二极管来实现.并把这个电路系统通过四个微分方程来描述,分析了系统的平衡点以及Lyapunov指数的特性.

1990年,Pecora 和Carrol在国际著名期刊Phys Rev Lett发表论文,通过反馈控制,实现了混沌同步.近年来混沌控制与同步得到广泛的研究,提出了许多混沌同步的方法[4～6],例如: OGY方法、微分几何方法、时间延迟方法、采样控制方法等,现在已经应用到保密通讯、信息处理、液体搅拌等领域[7,8].本文考虑了两个耦合的超Chua系统的同步,结合PC方法[4]和线性反馈控制,成功地将两个耦合的系统实现同步,数值仿真结果也验证了该方法的有效性.

1　基于Chua电路的超混沌系统

在经典的Chua系统的基础上,杨芳艳等人采用分段线性忆阻替换Chua 电路的电阻,提出一种简单的四维忆阻电路,通过理论推导、数值分析和电路仿真,证实其中存在着超混沌现象.系统可用如下方程组描述:

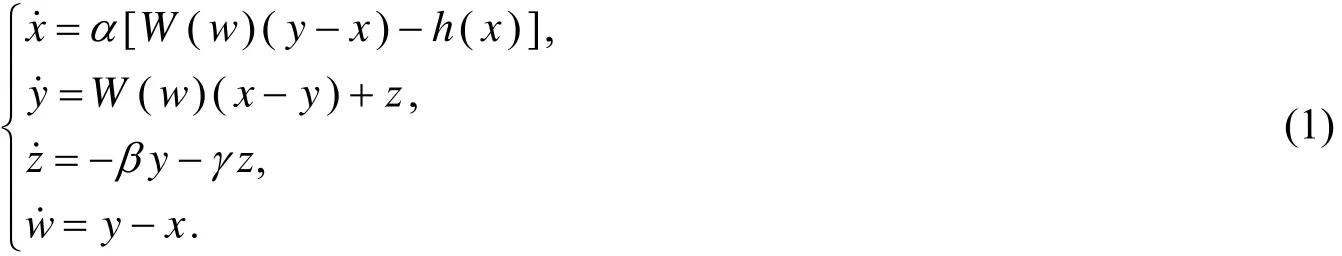
图1 系统的相图

2　基于线性反馈的同步研究

结合Pecora 和Carrol提出的方法[4],同时应用线性反馈控制方法,研究两个耦合的超Chua系统的同步,首先定义驱动系统为:

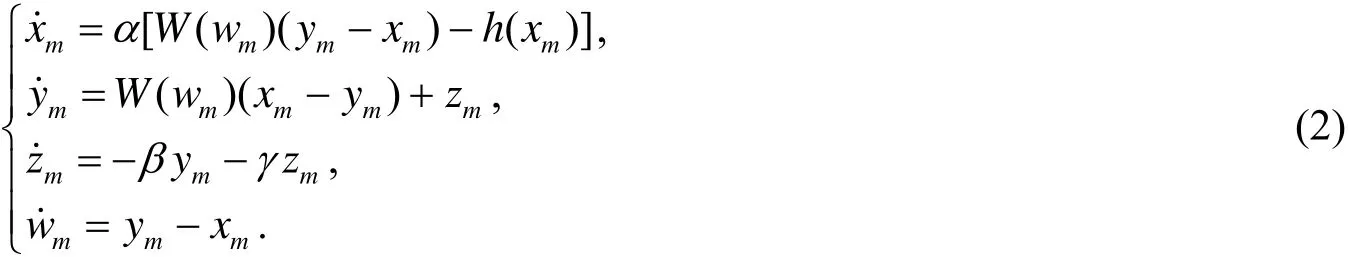
同时定义相应系统为:

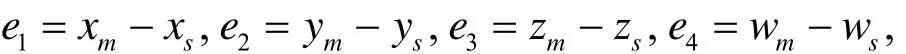
现在考虑如何选择适当的反馈增压强度,使系统(4)达到稳定零点状态,由此得到系统(2)和(3)是同步的.

定理 若混沌系统(2)是有界的,则一定存在适当的反馈强度ki≥0,i = 1,2,3,4,使得系统(2)和(3)是同步的.

其中

选择适当的ki≥0(i = 1,2,3,4),使得矩阵A的对角线元素为负值且严格对角占优.根据Gerschgorin圆盘定理[9],可得矩阵A是负定的.

3　数值仿真

为了验证上述结果的有效性,选取参数如下:

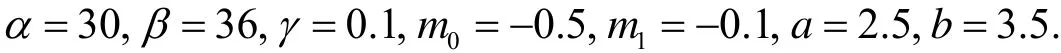
驱动系统和耦合系统的初值在[- 2,2]内随机选取,我们发现系统在适当的反馈增益下能很快到达同步状态.仿真结果如图2所示.

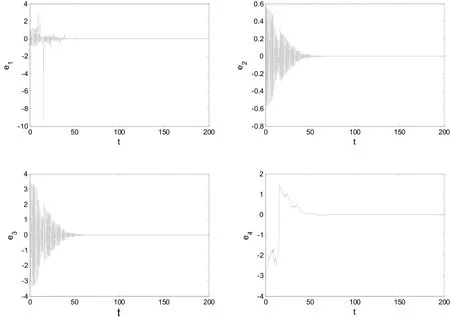
图2 驱动系统和耦合系统的误差图

4　结论

利用线性反馈控制和PC方法,本文研究了一个新的超混沌系统的同步.借助于Lyapunov函数稳定性分析方法,给出了达到同步的充分条件,数值仿真也验证了该结果的有效性.为超混沌系统在保密通讯、电路分析等中的应用提供了相应的理论基础.

参考文献

[1] Chua LO,Itah M.Chaos synchronization in Chua’s circuits[J].J Circ Syst Comput 1993; 3: 93～108

[2] Chua LO,Yang T,Zhong G.Adaptive synchronization of Chua’s oscillators[J].Int J Bifurcat Chaos 1996; 6: 189～201

[3] 杨芳艳,冷家丽,李清都.基于Chua电路的四维超混沌忆阻电路[J].物理学报,2014; 63: 080502

[4] Pecora LM,Carrol TL.Synchronization in chaotic systems[J].Phys Rev Lett 1990; 64: 821～824

[5] Ott E,Grebogi C,Yorke JA.Controlling chaos[J].Phys Rev Lett 1990; 64: 1196～1199

[6] Fuh CC,Tung PC.Controlling chaos using differential geometric method[J].Phys Rev Lett 1995; 75: 2952～2955

[7] Yau H,Wang M,Wang T,Chen G,Signal clustering of power disturbance by using chaos synchronization[J].International Journal of Electrical Power &Energy Systems,2015,64: 112～120

[8] Wu G,Baleanu D,Chaos synchronization of the discrete fractional logistic map[J].Signal Processing,2014,102: 96～99

[9] 刘丁酉.矩阵分析[M].武汉: 武汉大学出版社,2003

Synchronization of a Hyperchaotic System Based on Chua Circuit

ZHAO Jun-chan1,WEI Yao-bin2,XIE Xiao-liang1,LUO Zhi-ming1
(1.College of Mathematics and Statistics,Hunan University of Commerce,Changsha 410205,China 2.College of Mathematics and Computer Science,Wuhan Textile University,Wuhan 430072,China)

Abstract:Chua circuit has a wide range of applications,and has received more and more attention of researchers.With the help of the memristor,the researchers constructed a new hyperchaotic system based on Chua circuit.Through the PC control and linear feedback method,the synchronization of two chaotic systems with linear coupling is analyzed.Finally,the validity of the theoretical analysis is verified by numerical simulations.

Key words:Chua circuit,hyperchaotic system,synchronization

作者简介:赵军产(1982−),男,河南漯河人,博士,湖南商学院数学与统计学院副教授.主要研究方向: 混沌系统的控制与同步

基金项目:国家自然科学基金资助项目(61203159)

收稿日期:2015-10-30

中图分类号:O415.5

文献标识码:A

文章编号:1672-5298(2016)01-0017-04