三种Multiquadric拟插值多项式的再生性

王斯雯,陈荣华

(湖南科技大学 数学与计算科学学院,湖南 湘潭411201)



三种Multiquadric拟插值多项式的再生性

王斯雯,陈荣华

(湖南科技大学 数学与计算科学学院,湖南 湘潭411201)

摘 要:先研究了三种已知的Multiquadric拟插值的再生性,然后对三种已知的Multiquadric拟插值进行了推广,进一步讨论推广后的拟插值多项式的再生性,得到了如下结果: LA不是常数再生的; 当a + b = 1时,LD是常数再生的,但非线性再生的; 当a =,b =时,LD是线性再生的,但非二次多项式再生的.

关键词:拟插值; 多项式再生; 常数再生; 线性再生.

引言

拟插值方法[3,5]常被用于数值逼近中,有关Multiquadric(简称MQ)拟插值的研究大约始于上世纪80年代[2],Hardy在1971年最先提出了Multiquadric[4].影响力比较大的的是Powell和Beatson[1]构造的LA、LB、 LC以及Schaback与吴宗敏[7]得到的LD.Liu Jian-pin与吴宗敏[8]给出了无穷等距结点的MQ拟插值保形的充分条件.Ling[6]通过对LD进行多级处理得到了更好的结果.得益于文[7]的启迪,陈荣华与吴宗敏[3]通过构造一种与LD类似的拟插值后用于求解偏微分方程,得到了不错的结果.文[9]研究了某种特定形式的拟插值满足多项式再生性的充分必要条件,给出了几个结论,分别描述了常数再生、线性再生、二次多项式再生乃至一般的k次多项式再生的充分必要条件,并通过这些结论推出: LA不是常数再生的; LB是常数再生的,但非线性再生的; LD是线性再生的,但非二次多项式再生的.

本文先就三种Multiquadric拟插值LA、LB和LD进行研究,讨论其再生性.并对这三种Multiquadric拟插值稍作修改,讨论其保持相应的再生性需满足怎样的条件.

1　三种已知的Multiquadric拟插值及其推广

1.1 三种已知的Multiquadric拟插值

为了便于研究,先将三种已知的Multiquadric拟插值[1,7]罗列如下:

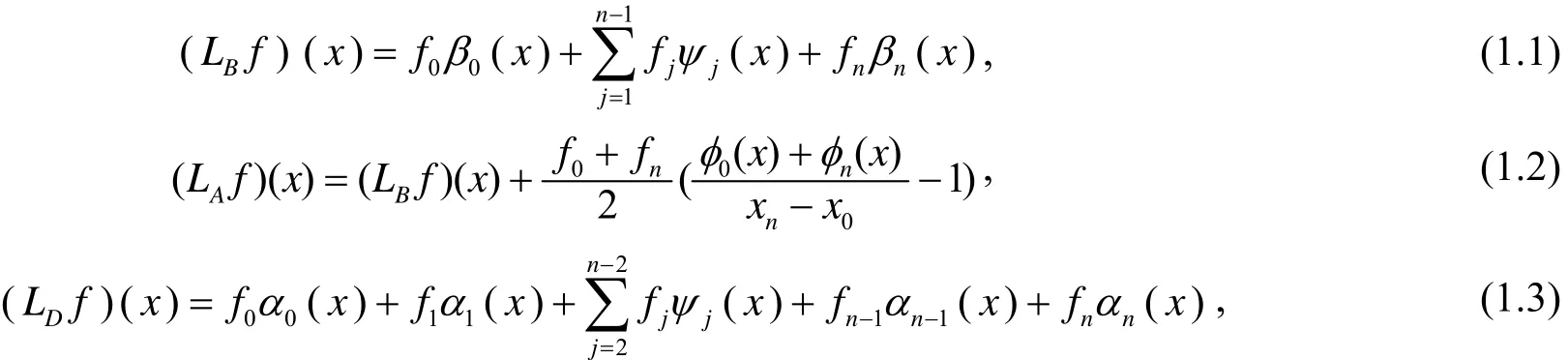
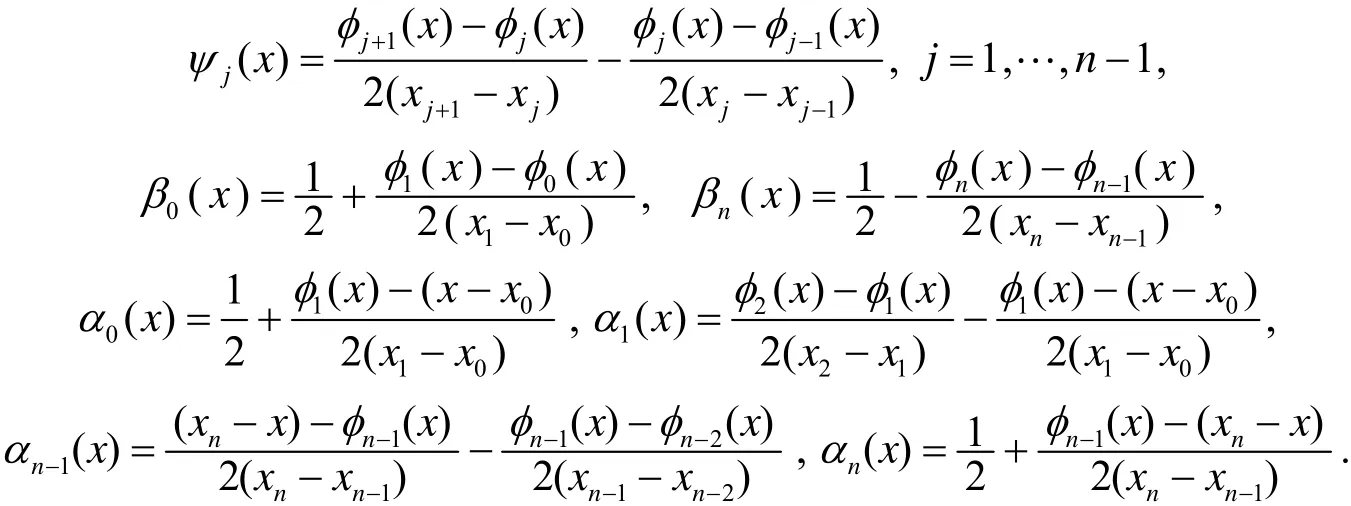
对于(1.1)及(1.2)式,有

对于(1.3)式,有

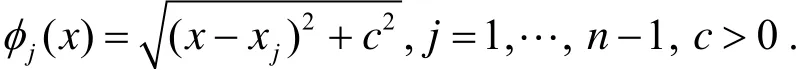
1.2 推广后的拟插值多项式

现在,将三种已知的Multiquadric拟插值[1,7]作如下修改:

2　拟插值保持多项式再生性的条件

2.1 多项式再生性

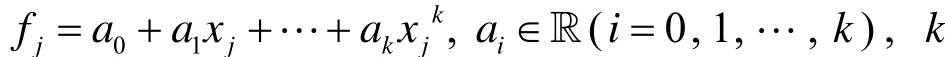
其中,零次多项式再生性也称为常数再生性,一次多项式再生性也称为线性再生性.

2.2 三种已知的Multiquadric拟插值多项式的再生性

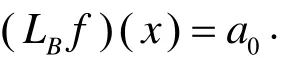
因此得到,LB是常数再生的.

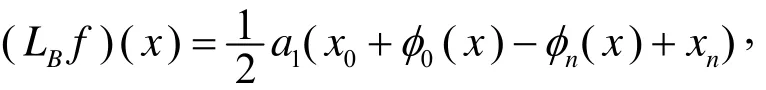
由(1.2)式知,LA不是常数再生的.

现在讨论LD.首先注意到,如果令

则(LDf)(x)可以改写为

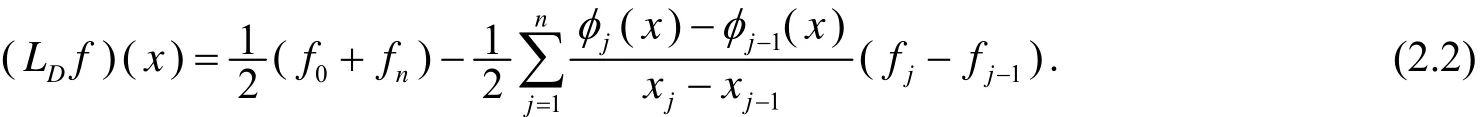
令fj=a0(j=0,1,…,n),代入(2.2)式中,得(LDf)(x)= a0.因此,LD是常数再生的.

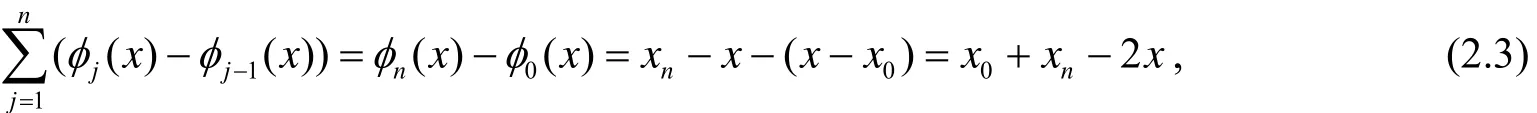
故有(LDf)(x)= a1x .因此,LD是线性再生的.

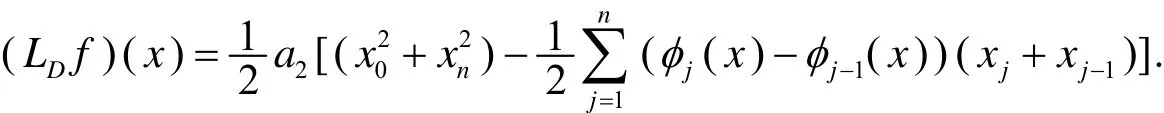
此时,(LDf)(x)= a2x2不是恒等式,因此,LD非二次多项式再生.

2.3 推广后的拟插值多项式的再生性

先讨论LB.令fj=a0(j=0,1,…,n),代入(1.4),得

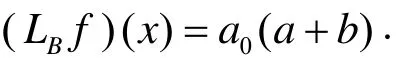
因此,当a+ b =1时,LB是常数再生的.

若fj=a1xj(j=0,1,…,n),代入(1.4),得

由(1.5)式知,LA不是常数再生的.

最后讨论LD.首先,在(2.1)的假定下,有与(2.2)式类似的结果,即

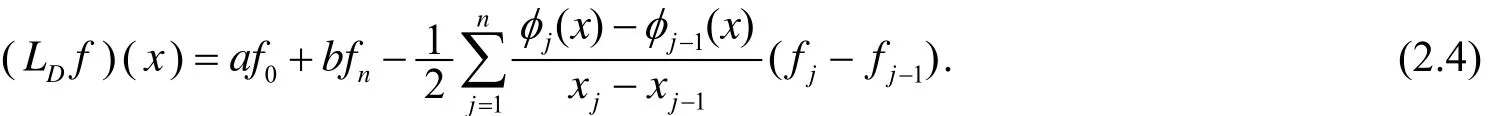
令fj=a0(j=0,1,…,n),代入(2.4),得

因此,当a+ b =1时,LD是常数再生的.

若fj=a1xj(j=0,1,…,n),代入(2.4),得

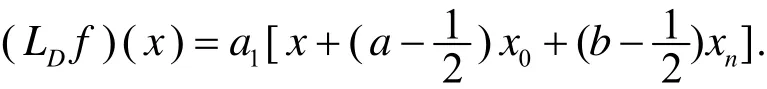
D

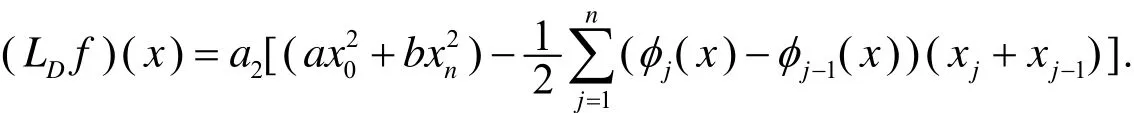
3　结论

本文首先研究了三种已知的Multiquadric拟插值的多项式再生性: LA不是常数再生的; LB是常数再生的但不是线性再生的; LD是线性再生的,但不是二次多项式再生的.其次对三种Multiquadric拟插值进行了推广,进一步讨论推广后的拟插值多项式的再生性: LA不是常数再生的; 当a+ b =1时,LB是常数再生的,但不是线性再生的; 当a= b =时,是线性再生的,但不是二次多项式再生的.也就是说,如(1.4)式那样定义的Multiquadric拟插值连常数再生都做不到;(1.5)式那样定义的Multiquadric拟插值虽然有无穷多个,只要满足条件a+ b =1即可,但它们都只能是线性再生的;(1.6)式定义的Multiquadric拟插值也有无穷多个,也只要满足条件a+ b =1即可,但要线性再生就只有一个,这就是吴宗敏及Schaback所定义的LD了,而且这样的Multiquadric拟插值只能是线性再生的.

当然,我们也可以仿照文[9]那样讨论形如(1.1)式那样的一般的拟插值保持多项式再生性所应该满足的条件,限于篇幅,这里不再赘述.

参考文献

[1] R.K.Beatson and M.J.D.Powell.Univariate multiquadric approximation: quasi-interpolation to scattered data [J].Constr.approx.,1992,8: 275～288

[2] M.D.Buhmann.Convergence of univariate quasi-interpolation using multiquadric [J].IMA J.Numer.Anal.,1988,8: 365～383

[3] R.H.Chen and Z.M.Wu.Solving hyperbolic conservation laws using multiquadric quasi-interpolation [J].Numerical Methods for Partial Differential Equations,2006,22: 776-796

[4] R.L.Hardy.Multiquadric equations of topography and other irregular surfaces [J].J.Geophysical Res.,1971,76: 1905～1915

[5] P.Lamberti and C.Manni.Tensioned quasi-interpolation via geometric continuity [J].Advances in Computational Mathematics,2004,20: 105～127

[6] L.Ling.A univariate multiquadric quasi-interpolation with better smoothness [J].Computers and Mathematics with Applications,2004,48: 897～912

[7] Z.M.Wu and R.Schaback.Shape preserving properties and convergence of Univariate multi-quadric quasi-interpolation [J].ACTA.Math.Appl.Sinica,1994,10: 441～446

[8] Z.M.Wu and J.P.Liu.The shape preserving and high accuracy approximation with multiquadric [J].Appl.Math.JCU,1996,11B: 217～224

[9] 陈荣华,韩旭里,吴宗敏.某型拟插值的多项式再生性[J].计算机工程与应用,2010,46(1): 1～3

Property of Polynomial Reproducing for Three Kinds of Multiquadric Quasi-interpolation

WANG Si-Wen,CHEN Rong-Hua
(College of Mathematics and Computational Science,Hunan University of Science and Technology,Xiangtan 411201,China)

Abstract:In this paper,we study the property of polynomial reproducing for three kinds of known MQ quasi-interpolation firstly,and deduce that LAisn't constant reproducing,LBis constant reproducing but not linear reproducing.LDis linear reproducing but not quadratic polynomial reproducing.Next to modifying the three kinds of MQ quasi- interpolation,further discussion property reproducing of the modified quasi-interpolation polynomial,and deduce that LAisn't constant reproducing; LBis constant reproducing but not linear reproducing when a + b = 1; LDis linear reproducing but not quadratic polynomial reproducing

Key words:quasi-interpolation,polynomial reproducing,constant reproducing,linear reproducing

作者简介:王斯雯(1989−),女,湖南邵东人,湖南科技大学数学与计算科学学院硕士研究生.主要研究方向: 数值逼近,微分方程数值解

收稿日期:2015-10-28

中图分类号:O174.42

文献标识码:A

文章编号:1672-5298(2016)01-0009-03