一类具有对数奇异的高振荡积分的高性能计算

李松华,刘佳倩,肖高玉

(湖南理工学院 数学学院,湖南 岳阳 414006)



一类具有对数奇异的高振荡积分的高性能计算

李松华,刘佳倩,肖高玉

(湖南理工学院 数学学院,湖南 岳阳 414006)

摘 要:根据第一类0阶Hankel函数的渐近性态,将原积分分解为两部分: 一是具有对数奇性部分,另一是不具有对数奇性部分.然后利用Filon方法,得到了一类具有对数奇异的高振荡积分的一种非常有效的数值方法,并研究该数值方法的收敛性,数值例子表明该数值方法非常有效.

关键词:对数奇异; 高振荡积分; Filon法

引言

电磁、声散射问题具有深刻的理论价值和重要的应用背景,其数学模型可用Maxwell方程、Helmholtz方程以及具有高振荡核的积分方程加以描述.积分方程是求解电磁、声散射问题的有力工具,尤其对于高频散射问题,其数值解法均涉及高振荡积分的高性能计算[1,2].

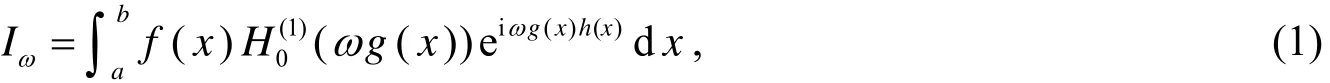
针对积分(1)的数值计算,S.N.Chandler-Wilde等在文[2]中讨论了g(x)在积分区域[a ,b ]没有零点的情形.在一定条件下,可以采用公式

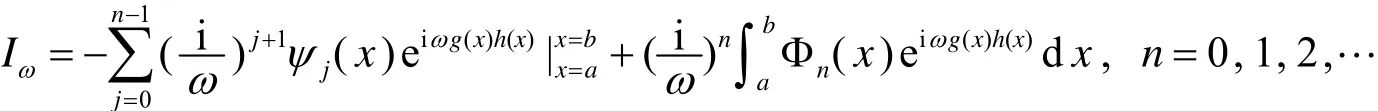
计算.其中

若函数g(x)在区间[a ,b ]有一个或多个稳定点,不妨设ζ0∈[a ,b ]是g(x)在区间[a ,b ]上唯一稳定点,由文[4]可知,存在正整数r ,使得

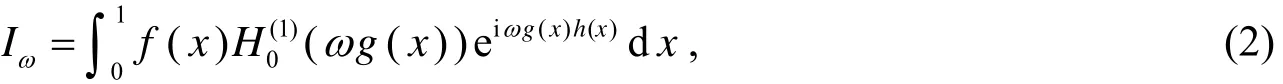
1　函数　H　0(1)(ω　g(x))的分解

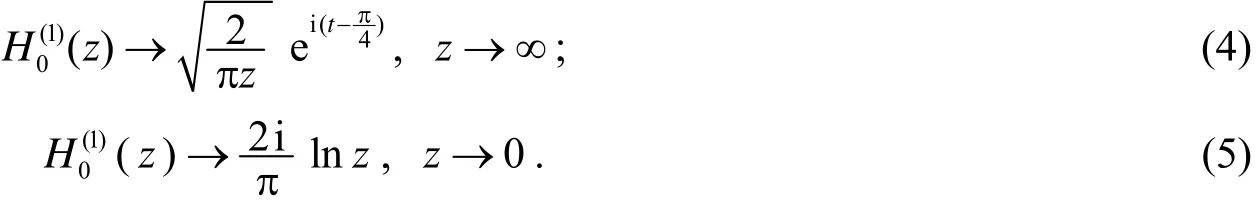
其中

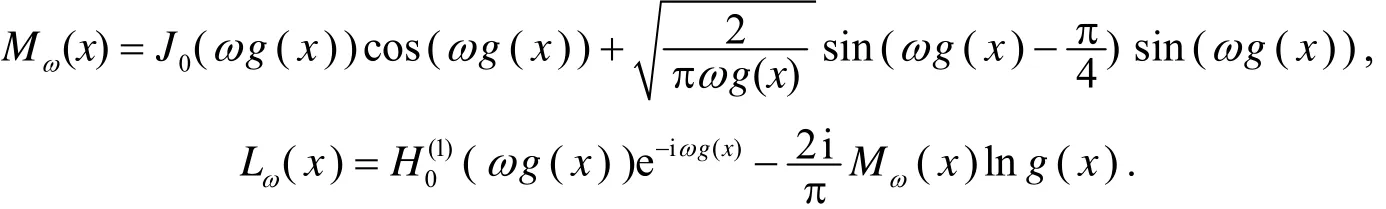
图1 　H　0(1)(ω　g(x))与　H　0(1)　(ω　g(x))e-　　i ωg(x)的实部和虚部

将(6)式代入(2)式,可得

本文只考虑在积分区间(0,1]上1+h(x)＞ 0的情形.这是因为对于有界函数h(x),存在正常数d使得d+ h(x)＞ 0,于是

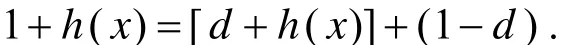
式(7)中的积分Iω可进一步改写为

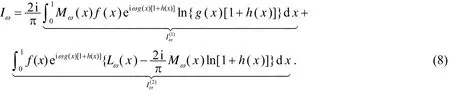
2　Filon型方法

其中

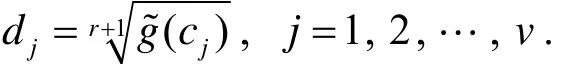
那么关于积分(9)的Filon型积分定义为:

注 若用Filon型积分方法计算I(2)ω,则需计算矩

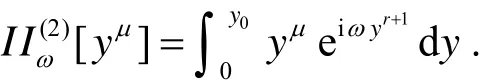
μ

其中l=1,2,…,mμ- 1.

其中C是与波数k无关的常数.

为了证明上述定理,需要如下引理.

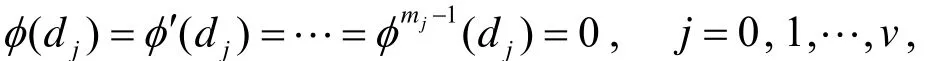
则

其中ζ∈[0,y0].

证明 由引理中式(13),可知

从而可得

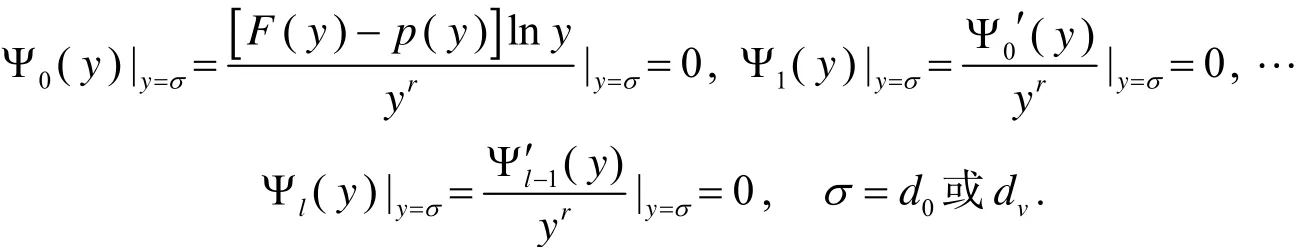
再利用分部积分法与式(10),可得

故误差估计式(12)成立.

3　数值例子

在积分式(2)中f(x),g(x)和h(x)分别为

其中M =1,2,… .

4　结语

从图3可以看出,本文所提出的Filon型方法在计算高振荡积分(2)时非常有效,尤其是振荡频率越高算法精度愈高,可望为电磁计算的研究提供一些新的高效算法.

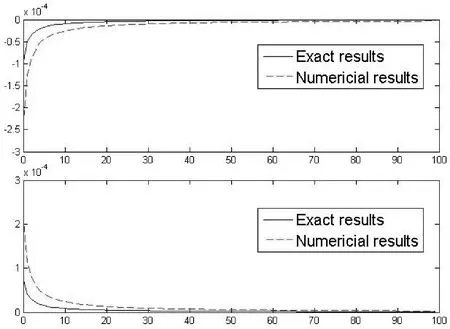
图3 上图表示二者的实部,下图表示二者的虚部,其中横坐标为　x =　1,2,… 　,100,此时对应的ω值为　ω=　10000 + 10000x

参考文献

[1] 向淑晃.一些高振荡积分、高振荡积分方程的高性能计算[J].中国科学: 数学,2012,42(7): 651～670

[2] S.N.Chandler-Wilde,I.G.Graham,S.Langdon,and E.A.Spence.Numerical-asymptotic boundary integral methods in high-frequency acoustic scattering[J].Acta Numer.,2012,21,89～305

[3] 李松华,郭 涛,符江鹏.一类高振荡积分的快速数值方法[J].湖南理工学院学报(自然科学版),2013,26(1): 18～21

[4] E.Stein.Harmonic Analysis: Real-variable methods,orthogonality,and oscillatory integrals[M].Princeton University Press,Princeton,1993

[5] D.Colton and R.Kress.Inverse Acoustic and Electromagnetic Scattering Theory[M].Springer-Verlag Berlin Heidelberg,1998

[6] M.Abramowitz,I.A.Stegun.Handbook of Mathematical Functions[M].National Bureau of Standards,Dover Publications,1965

A Efficient Method of Highly Oscillatory Integrals with Logarithmic Singularity

LI Song-Hua,LIU Jia-Qian,XIAO Gao-yu
(College of Mathematics,Hunan Institute of Science and Technology,Yueyang 414006,China)

Abstract:Based on asymptotic behavior of the Hankel function of the first kind of order zero,we split the integral into two parts: one is the part with logarithmic singularity; the other is the part without singularity.A fast numerical integral method for highly oscillatory integral with logarithmic singularity is obtained by using the Filon-type method.Furthermore,the convergence of the numerical method is investigated.Examples are given to demonstrate that the numerical method has good effectiveness and accuracy.

Key words:logarithmic singularity,highly oscillatory integrals,Filon method

作者简介:李松华(1973−),男,湖南邵阳人,博士,湖南理工学院数学学院教授.主要研究方向: 小波分析和偏微分方程数值解

基金项目:湖南省自然科学基金项目(2016JJ4037); 湖南省教育厅项目(15A077)

收稿日期:2015-12-28

中图分类号:O241.4

文献标识码:A

文章编号:1672-5298(2016)01-0004-05