从大纲到课标：初中“二次根式”学习要求的比较研究

胥朋飞

（贵州师范大学数学与计算机科学学院，贵州 贵阳 550001）

二次根式的学习早就进入了中学数学课本，但从学生平时的练习和考试情况来看，很多学生在这些知识点上存在概念不清、计算出错等问题。

1 不同版本大纲和课标对二次根式学习的要求

在教育部审定的北师大2013 版教材中，二次根式的学习主要开始于八年级上册第二章第7 小节，对于二次根式内容的学习，不同版本大纲和课程标准给出了不同的目标和要求，分别如下：

1992年教育部颁布的《九年义务教育全日制初级中学数学教学大纲（试用版）》中指出：（1）了解二次根式、最简二次根式、同类二次根式的概念，会辨别最简二次根式和同类二次根式；（2）掌握二次根式的性质，如：（a≥0，b＞0），会根据二次根式的性质熟练地化简二次根式（如无特别说明，根号内所有的字母都表示正数，并且不需要讨论）；（3）掌握二次根式的加、减、乘、除的运算法则，会用它们进行运算；（4）会将分母中含有一个或两个二次根式的式子进行分母有理化。[1]

2000年教育部颁布的《九年义务教育全日制初级中学数学教学大纲（试用修订版）》中指出：（1）了解二次根式、最简二次根式、同类二次根式的概念，会辨别最简二次根式和同类二次根式；（2）掌握积与商的方根的运算性质，如：（a≥0，b＞0），会根据这两个性质熟练地化简二次根式（如无特别说明，根号内所有的字母都表示正数，并且不需要讨论）；（3）掌握二次根式（不含双重根号）的加、减、乘、除的运算法则，会用它们进行运算；（4）会将分母中含有一个二次根式的式子进行分母有理化；（5）掌握二次根式的性质，会利用它化简二次根式。[2]其中，最后一条被列为选修部分。

2001年教育部颁布的《全日制义务教育数学课程标准（实验稿）》（简称标准）在第三学段的内容标准中提出：了解二次根式的概念及其加、减、乘、除运算法则，会用它们进行有关实数的简单四则运算（不要求分母有理化）。[3]

2011年版《义务教育数学课程标准》（简称《新标准》）也提出：了解二次根式、最简二次根式的概念，了解二次根式（根号下仅限于数）加、减、乘、除运算法则，会用它们进行有关的简单四则运算。[4]

2 不同版本大纲、课标之间二次根式学习内容的比较

2.1 不同大纲二次根式学习内容的异同点

通过比较，大纲都要求学生了解一些相关的定义和概念，如二次根式、最简二次根式等，重点是让学生在运用之前把基础知识打牢。在运算性质中，修订版的大纲中取消了这一条，明确指出“会根据这两个性质（积和商）熟练地化简二次根式”。而在1992年的试用版大纲中，没有确切的提出“两个性质”，这样，学生在做题时所接触的知识点就会有所减少，难度也会有所下降，给学生减轻了负担。对比两个版本大纲，在掌握二次根式性质中，大纲中都附有一个括号，以此特别要求学生在计算过程中，要清楚知道根号下面的字母必须是正数，才可以进行化简计算，这也是大部分学生的一个易错点。对于运算法则，修订版的大纲明确提出二次根式的计算中不能有双重根号，在进行分母有理化时也只是要求学生会将分母中含有一个二次根式的式子进行分母有理化，难度降低。

2.2 不同课标二次根式学习内容的异同点

概念掌握对学生后续学习是非常重要的，因此在新旧标准中，它们都明确要求学生必须了解二次根式的概念。在新标准中，加入了要让学生了解“最简二次根式的概念”。在加、减、乘、除运算法则中，新课标特意指出在计算中“根号下仅限于数”，就把根号下有字母的运算给取消了。同时，新旧标准都要求学生会进行简单四则运算，不同的是，标准中指出“不要求分母有理化”，而新标准中却没有提到这一条。

对比标准和新标准，在概念方面，新标准加入了一个知识点“了解最简二次根式的概念”，拓宽了学生的知识面，对二次根式有更进一步的要求和理解。在运算法则方面，取消了字母运算，回归学生熟悉的数字运算，难度大大降低，减轻学生的学习负担，但也加入了一个难点“分母有理化”,这对学生来说是一个大的挑战，成为大部分学生在二次根式学习中所遇到的一个困难。综合来看，新标准对学生提出了更高的要求。

2.3 不同版本大纲与课标之间二次根式学习内容的异同点

在数学知识学习中，一些基本的概念是学生所必须掌握的。因此，无论是大纲还是标准，对此都作了严格的规定，要求学生必须了解。只是在两版的大纲和标准中，只有标准是没有明确指出要学生“了解最简二次根式的概念”的。在数学计算中，总是离不开性质和法则，大纲和标准都有所规定，而最大的不同就是在分母有理化这一知识点的要求上，标准中没有要求分母有理化，新标准和两版的大纲都有所要求，但在1992年的试用版大纲中，要求学生“会将分母中含有一个或两个二次根式的式子进行分母有理化”，这是学生在学习中难度最大的。

对比两个版本大纲和标准，标准在内容的学习上有所减少，但对学生所要学习二次根式的最基本要求没有改变，难度有所降低，但要求学生掌握的计算过程和基本运算法则没有改变。

3 典型案列分析

二次根式的运算是初中数学学习的一个重点和难点，是对所学概念、性质和运算法则的终极运用点，更是已学的“数与式”内容的延伸和综合体现。[5]因此，在学习中还需要把已学过的知识融入其中，引导学生更好的去学习。

3.1 概念、性质的运用

新课标要求学生要了解二次根式、最简二次根式的概念，特别是最简二次根式。在初中的数学教学中，所涉及到的题目也是最多的，因为它既是二次根式加减法运算的基础，也是我们在做题时对运算结果的一种要求，为二次根式的运算指明了方向。对于最简二次根式的概念，在教育部审定的北师大2013版教材中第42 页提到：“一般地，被开方数不含分母，也不含能开得尽方的因数或因式，这样的二次根式，叫做最简二次根式。一般地，被开方数不含分母，也不含能开得尽方的因数或因式，这样的二次根式，叫做最简二次根式”。[6]，对于二次根式的化简，我们必须要求学生首先掌握二次根式的两个常用性质：0，b＞0），这样才能方便学生更好的解题，但由于许多学生对概念、性质等基础知识掌握不牢，就经常会出现许多错误，比如

例1：（2010年湛江） 下列二次根式是最简二次根式的为（ ）

错解 1：D 错解 2：A

解析：根据最简二次根式的定义：一般地，被开方数不含分母，也不含能开得尽方的因数或因式，这样的二次根式，叫做最简二次根式。选项D 中学生认为不能继续化简出错，选项A 中学生对最简二次根式的定义不清晰出错，被开方数不含分母。

例2：化简

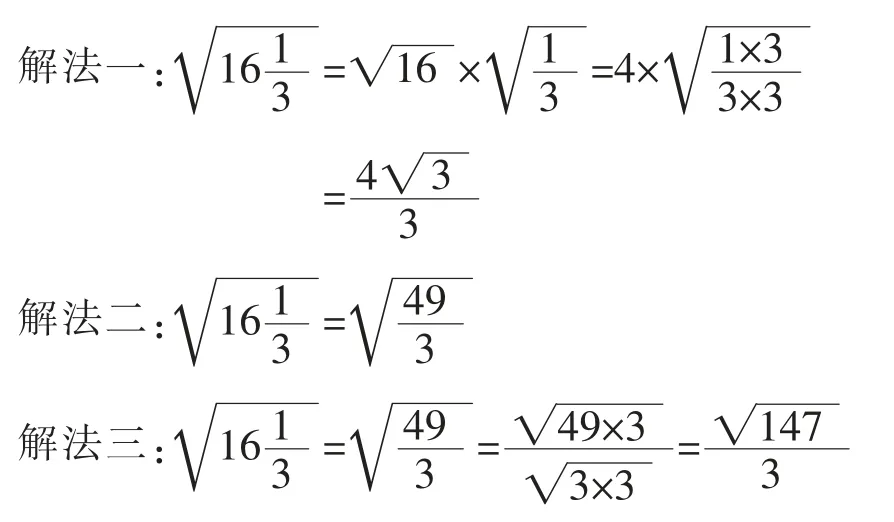
解析：以上都是学生经常会出错的几种解法，解法一中学生对带分数理解不清晰，直接想到用二次根式的乘法性质而出错；解法二中学生没有认识到“被开方数中不含分母”而出现错误；第三种解法出错几率很高，大部分学生都会认为分子的不能再做化简，而，因此正确答案应该为。

3.2 法则的运用

二次根式乘法法则和除法法则的运用主要在课本的第2 课时，是在第1 课时二次根式性质的基础上的直接运用，新标准要求会用二次根式的加、减、乘、除运算法则进行计算，在课本中给出了3 个例题，例3 的3 个小题是对二次根式乘法法则和除法法则的直接运用计算，相对来说比较简单，而例4 和例5 中的几个小题除了乘、除运算，还加入了加、减运算，题目的设计具有一定的梯度，例4 侧重乘、除运算，同时也加入了学生很熟悉的有关运算定律和公式（如结合律、交换律、分配率、平方差公式和完全平方式等）的运用；而例5 主要为加、减运算，不同的是，算到最后结果有同类二次根式，可以进行合并。在对二次根式法则的运用中也常常会出现许多的错误，举例如下：

解析：解法一中学生直接按照以前熟悉的整数运算进行分子分母约分，不清楚根号内的因数不能和根号外的因数直接进行约分出错；解法二中学生在进行到最后时忘记了带运算，在进行合并同类二次根式时被开方数和根指数都不变，因此正确结果为

解析：解法一中学生没有认识到和不是同类二次根式，所以不能合并，更不能违反运算法则直接把被开方数相加；解法二中是因为学生对以前学过的完全平方式记忆不清晰而运用出错；解法三中学生把二次根式的乘法法则误用到加法中而出现错误。正确的解答过程为

结果不是同类二次根式，不能再进行合并了。

通过对相关典型案例的分析可以看出，学生要能够熟练掌握二次根式的概念、性质和法则，同时应该把以前学过的知识点融入进去，否则在运用的过程中就会出现错误。二次根式在初中数学的学习中有着非常重要的位置，在后续的教学中也还会有进一步的加深运用，对大部分中学生来说比较困难，因此，在教学过程中，教师应该进行合理的讲解，不要让学生只是机械性的死记硬背，要让学生在熟练中运用，在运用中熟练，找到适合的解题思路和过程，提高学生的思维能力和计算能力，避免出现一些基础性的错误。