解答空间几何问题的几个策略
☉江苏省如皋市第二中学王晓红
解答空间几何问题的几个策略
☉江苏省如皋市第二中学王晓红
立体几何是高考主干知识之一,在历年各省市的高考试卷中常以一大一小两种类型题出现,其中主要涉及由三视图求几何体的面积或体积、空间平行或垂直关系的判断,以及空间距离、空间角问题的求解.试题在突出对空间想象能力考查的同时,关注对平行、垂直的探究,关注对条件和结论不完备情形下开放性问题的探究.熟练掌握此类问题的常规处理策略,常可快速找到问题的突破口.
本文将从解题思路的寻找入手,就此类问题的解答提几点建议,供同学们参考.
一、构造特殊模型突破三视图的空间想象
对学生的空间想象能力有较高的要求,考生通过读三视图,想象真实几何体,并计算几何体的表面积或体积等.三视图看起来简单,但还原几何体有一定的难度.
例1一个棱锥的三视图如图1所示,则该棱锥的全面积(单位:cm2)为().

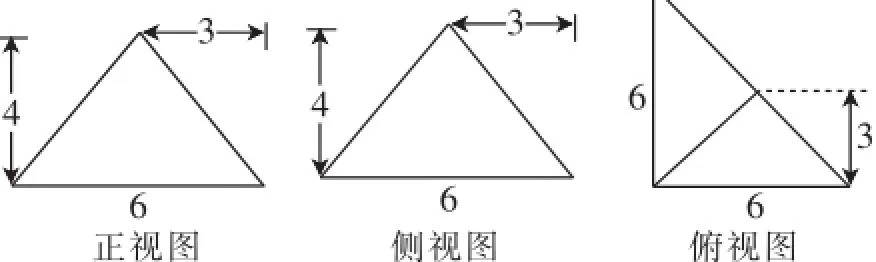
图1
解析:空间三视图问题的考查,多以特殊几何体为背景,解答此类问题时,若能正确构造出原几何体,则可将三视图中的信息准确直观地反映出来.构造长方体,则题目中的三棱锥如图2中的S-ABC,由图易知15,所以三棱锥S-ABC的全面积为
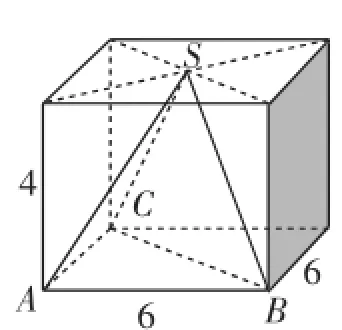
图2
点评:准确地将三视图还原于常规几何体中,是求解此类问题的关键,所谓的常规几何体通常指长方体、正方体等.要求空间几何体的体积,首先要由三视图还原空间几何体,同时还要由视图中标注的数字反映出空间几何体的几何元素的数量,解题中就是要把这种数量关系找出,这就需要空间想象能力.特别提醒:画三视图时,要注意看到的轮廓线画成实线,看不到的轮廓线画成虚线.
二、熟练把握相关原理以不变应万变
例2如图3,在四棱锥P-ABCD中,底面四边形ABCD的两组对边均不平行.
①在平面PAB内不存在直线与DC平行;
②在平面PAB内存在无数多条直线与平面PDC平行;
③平面PAB与平面PDC的交线与底面ABCD不平行;

图3
上述命题中正确命题的序号为_________________.
解析:是否存在问题的常用处理策略:先假设所给结论成立,再逆向判断其与所给条件相符或矛盾即可.
①假设在平面PAB内存在直线l与DC平行,由线面平行的判断可知CD平行于面PAB.又CD⊂面ABCD,面ABCD∩面PAB=AB,所以CD∥AB,与已知条件矛盾,故在平面PAB内不存在直线与DC平行,①正确.
②由条件知面PAB与面PCD相交,设交线为m,作平行于m的平面与两平面均相交,易知两交线平行,而这样的平面有无数个,故存在无数条交线相互平行,故②正确.
③假设面PAB与面PCD的交线为n,若直线n与底面平行,则n∥AB,n∥CD,所以AB∥CD,与条件矛盾,故平面PAB与平面PDC的交线与底面ABCD不平行,故③正确.
答案:①②③.
点评:空间平行关系包括线线平行、线面平行、面面平行,三种关系可以相互推导.本题的顺利求解,源于对空间平行关系的灵活应用.
三、动中寻定探究动态几何问题
例3在边长为2的正方体ABCD-A1B1C1D1中,E为BC的中点,点P在底面ABCD上移动,且满足B1P⊥D1E,则线段B1P的长度的最大值为().

解析:对于动态问题的解答要抓住其中不变的因素,如本题中点P为面ABCD内的动点,但B1P⊥D1E,因此B1P在一个与D1E垂直的定面上.找到这个定面即可顺利解决问题.
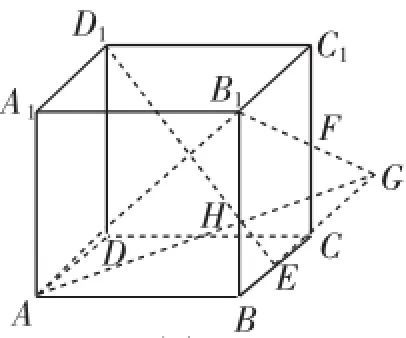
图4
如图4,取CC1的中点F,连接B1F并延长交BC的延长线于点G,连接AG交CD于点H,连接AB1.
易知D1E⊥AB1,D1E⊥B1F,所以D1F⊥面AB1G,即点P在线段AH上.
又△GCF∽△GBB1,△GHC∽△GAB,最大值为3,故选D.
点评:定线与动线垂直,即动线在与定线垂直的定面内,找到这个定面使得问题顺利求解.类似地,若动线与已知面平行,则动线在与已知面平行的定面内等.只要抓住这些动态问题中的不变因素,即可找到问题的求解思路.
四、用运动变化的观点解决空间图形问题
考纲对考生的空间想象能力的考查提出了“能够想象几何图形的运动和变化情况”的更高要求.因此,立体几何题中除固定的线线、线面、面面关系外,还渗透了一些“动态”的点、线、面元素,给“静态”的立体几何赋予了新的活力,新的亮点.
例4如图5,已知△ABC,D是AB的中点,沿直线CD将△ABC折成△A′CD,所成二面角A′-CD-B的平面角为α,则().
A.∠A′DB≤αB.∠A′DB≥α
C.∠A′CB≤αD.∠A′CB≥α
解析:设∠ADC=θ,AB=2,则由题意知AD=BD=1,在空间图形中,设A′B=t,在△A′CB中,

图5

图6
在空间图形中,如图6,过点A′作A′N⊥DC,过点B作BM⊥DC,垂足分别为N、M,过点N作NP∥=MB,连接A′P,所以NP⊥DC,则∠A′NP就是二面角A′-CD-B的平面角,所以∠A′NP=α.
在Rt△A′ND中,DN=A′D·cos∠A′DC=cosθ,A′N= A′Dsin∠A′DC=sinθ.
同理,BM=PN=sinθ,DM=cosθ,故BP=MN=2cosθ.
显然BP⊥面A′NP,故BP⊥A′P.
在Rt△A′BP中,A′P2=A′B2-BP2=t2-(2cosθ)2=t2-4cos2θ.

因为α、∠A′DB∈[0,π],而y=cosx在[0,π]上为减函数,所以α≤∠A′DB,故选B.
点评:本题主要考查立体几何中的动态问题,属于较难题,由于△ABC的形状不确定,∠A′CB与α的大小关系也是不确定的,再根据二面角的定义,可知∠A′DB≥α,当且仅当AC=BC时等号成立,以立体几何为背景的创新题是浙江高考数学试卷的热点问题之一,解决此类问题需在平时注重空间想象能力的培养,加强此类问题的训练.
五、借助空间向量寻求几何问题代数化处理
由于空间向量的引入,在立体几何的教学中出现了重视计算,忽视空间想象能力培养,削弱立体几何推理教学的现象,这使得考生推理证明能力与空间想象能力有所下降,这就要求我们在教学中对必修阶段立体几何初步的定位要因学生情况而异.
例5如图7所示的几何体中,2CC1=3AA1=6,CC1⊥平面ABCD,且AA1⊥平面ABCD,正方形ABCD的边长为2,E为棱A1D的中点,平面ABE分别与棱C1D、C1C交于点F、G.
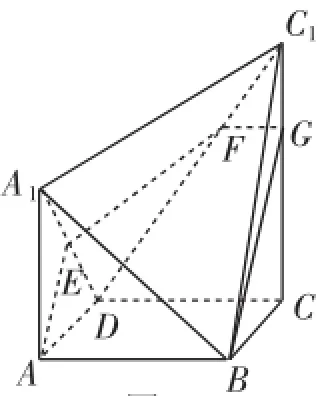
图7
(1)求证:A1D⊥平面ABE;
(2)求二面角D-EF-B的大小,并求CG的长.
解析:(1)因为AA1⊥平面ABCD,所以AA1⊥AB,AA1⊥AD.因为ABCD是正方形,所以AB⊥AD.
以AB、AD、AA1分别x、y、z轴建立空间直角坐标系,则由已知可得B(2,0,0),D(0,2,0),A1(0,0,2),E(0,1,1),=(0,-2,2)(0,1,1),(2,0,0).
(2)因为A1D⊥平面ABE,且A1D⊂平面EFD,所以平面EFD⊥平面ABE.
因为平面ABE即为平面BEF,所以二面角D-EF-B的大小为90°.
点评:空间向量的引入使立体几何问题的求解更加程序化.通过建立空间直角坐标系,引入向量来解决空间垂直、空间角、空间距离问题,大大降低了问题的难度.如空间垂直问题可利用向量垂直原理,即数量积为0求解.二面角问题可借助其与两面法向量夹角相等或互补的原理求解.
总之,在空间几何问题的解答中,我们要关注“为什么要用这种解法,这种解法是如何想到的”,只有弄清楚这一问题,在解题时才能迅速找到切入点.因此,在平时解题训练中,要注重常用公式、性质、定理的变式应用,注重对常考题型的归纳、常用方法的总结,方可以不变应万变.F

