莫让浮云遮望眼,撩开雾纱见真颜
——一道解析几何模拟试题的深度探寻
2016-05-15 03:29:36浙江省杭州师范大学附属中学苏立标
中学数学杂志 2016年7期
☉浙江省杭州师范大学附属中学苏立标
莫让浮云遮望眼,撩开雾纱见真颜
——一道解析几何模拟试题的深度探寻
☉浙江省杭州师范大学附属中学苏立标
一、问题的呈现
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点A作AP//OM交椭圆C于点P,求证:BP//ON.
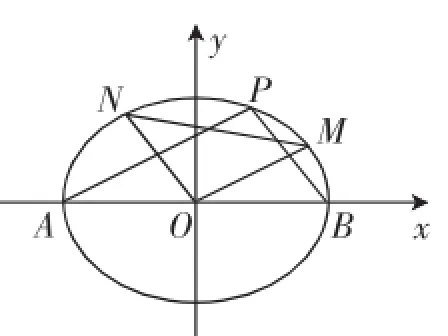
图1
(Ⅱ)证法1:如图2所示,由题意可设直线OM,ON的方程为y=kOMx,y=kONx.
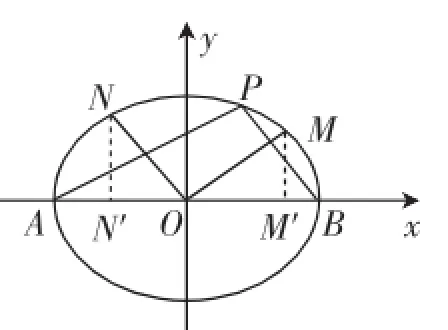
图2



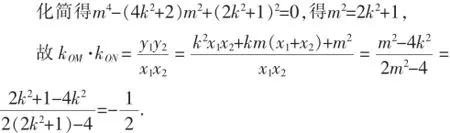
【点评】本试题虽然是一道模拟试题,但题目立意之新、内涵之广、选材之妙不得不令人叹服.以新颖的视角、创新的手法进行精心地构思,彰显新课程的理念,所以是一道创新而不落俗套的好试题,有利于甄别学生的思维层次,具有较好的区分度.这个问题反1(a>b>0)一组性质,不仅设计独特新颖,而且具有推广与引申的价值,可以演变出一组妙趣横生的结论.(本文中的字母e均为离心率)
二、问题的逆向探究
“探幽重门深锁无寻处,疑有碧桃千树花.”对于一个数学问题,需要多角度的剖析、探究.对于一个数学问题的探究思考,最基本的切入点就是对条件与结论进行变式思考,可以考虑逆命题是否成立.
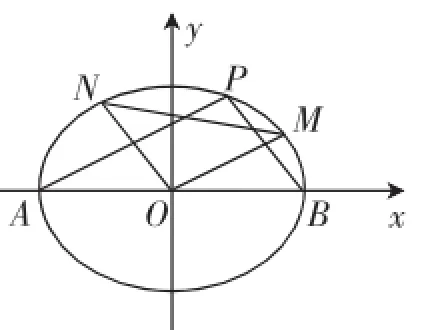
图3
(Ⅰ)求椭圆C的方程;
(Ⅱ)若椭圆C上的点P满足:AP//OM,且BP//ON,

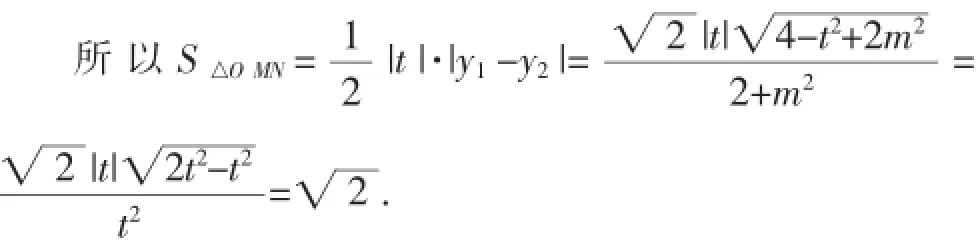
三、问题的一般化探究
为了能把问题看得更清楚些,我们往往考虑把问题进行一般化情形研究,容易得到下列结论:
P,求证:BP//ON.
【分析】由于kPAkPB=e2-
1,所以只需要证明kOMkON=e2-1.

图4


四、问题的本原探究
1.苏立标.博观而约取,厚积而薄发——以e2-1为定值的圆锥曲线高考试题赏析[J].中学数学(上),2013(3).G
猜你喜欢
保健医苑(2022年5期)2022-06-10 07:46:58
江苏教育(2021年54期)2021-08-31 10:12:32
中小学校长(2021年7期)2021-08-21 06:49:56
中学生数理化(高中版.高考数学)(2020年3期)2020-05-25 06:53:10
小学生作文(低年级适用)(2019年10期)2019-10-28 06:46:26
中学数学杂志(2019年1期)2019-04-03 00:35:42
商周刊(2018年26期)2018-12-29 12:56:00
快乐语文(2018年25期)2018-10-24 05:38:56
人大建设(2018年5期)2018-08-16 07:09:02
中学生英语·外语教学与研究(2017年3期)2017-05-19 23:18:46

