例谈高考对函数与方程的考查

☉江苏省张家港市沙洲中学曾艳辉

例谈高考对函数与方程的考查

☉江苏省张家港市沙洲中学曾艳辉

高中数学中《函数与方程》是重要内容，常常会考查函数的零点、方程的根和两函数图像交点之间的等价转化思想和数形结合思想.有时与函数的单调性、奇偶性、周期性结合研究方程根的分布区间或者零点的存在性、零点的个数问题考查；有时通过对方程根的分布情况的研究，综合考查不等式的求解、函数的图像与性质等问题.下面笔者结合自己的教学实践谈谈高考对函数与方程的考查，以期抛砖引玉.

一、判断函数零点个数或方程解的个数问题

判断函数零点个数的常用方法有三种：（1）解方程法；（2）零点存在性定理法：利用该定理不仅要求函数在区间［a，b］上是连续不断的曲线，且f（a）·f（b）＜0，还必须结合函数的图像与性质才能确定函数有多少个零点；（3）数形结合法：画出两个函数的图像，看其交点的个数.

例1设方程|x2-1|=k+1，试讨论k取不同范围的值时其不同解的个数的情况.

分析：我们可把这个问题转化为确定函数y1=|x2-1|与y2=k+1图像交点个数的情况，因函数y2= k+1表示平行于y轴的所有直线，如图1，从图像可以直观看出.

图1

解：①当k＜-1时，y1与y2没有交点，这时原方程无解；

②当k=-1时，y1与y2有两个交点，原方程有两个不同的解；

③当-1＜k＜0时，y1与y2有四个不同交点，原方程不同解的个数有四个；

④当k=0时，y1与y2有三个交点，原方程不同解的个数有三个；

⑤当k＞0时，y1与y2有两个交点，原方程不同解的个数有两个.

点评：数形结合是数学解题中常用的思想方法，使用数形结合的方法，很多问题能迎刃而解，且解法简捷.本题中将方程的解的问题转化为两个函数图像的交点个数问题，使得问题简单明了.

二、参数的值或取值范围问题

根据函数零点的存在情况，求参数的值，已知函数有零点（方程有根）求参数取值常用的方法和思路：（1）直接法：直接根据题设条件构建关于参数的不等式，再通过解不等式确定参数范围；（2）分离参数法：先将参数分离，转化成求函数值域问题加以解决；（3）数形结合法：先对解析式变形，在同一平面直角坐标系中，画出函数的图像，然后数形结合求解.

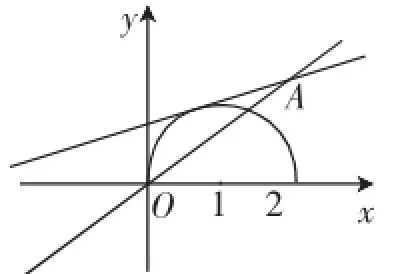
图2

点评：加强数形结合意识，做到脑中有图，借助方程的曲线，将图形性质与数量关系相结合可使复杂问题简单化，抽象问题具体化，达到化难为易，起到事半功倍的效果.

三、确定函数零点的区间，注重定理的运用

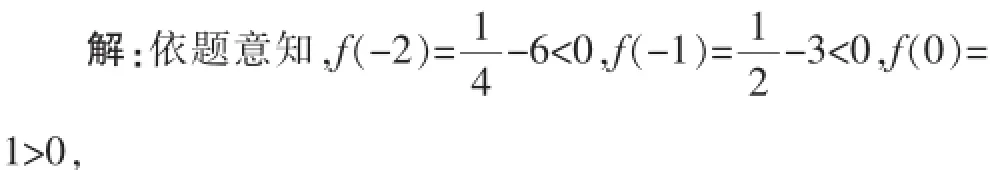
f（1）＞0，f（2）＞0，f（-1）·f（0）＜0，因此在区间（-1，0）上一定有零点.

点评：本题比较基础，直接根据零点存在定理求得.

确定函数零点所在的区间，常用的方法有三种：一是用定理，二是解方程，三是用图像.

例3函数f（x）=2x+3x的零点所在的一个区间是（）.

A.（-2，-1）B.（-1，0）

C.（0，1）D.（1，2）

四、考查与方程组相关的问题，渗透数形结合的思想

点评：此题解法关键是求出x+y+z，若用纯代数解法是极困难的，但构造三角形运用余弦定理便迎刃而解，充分体现了以平面图形助数的实效性.把数量关系的精确刻画与平面几何图形的形象直观有机地结合起来，便于充分揭露问题的条件与结论之间的内在联系（包括原有的隐含条件），在此基础上恰当地变更问题或变换解题角度，采用数形结合的手段来简化运算过程，提高解题速度.

五、借助零点，考查导数探究函数的性质

在此类问题中，分析与讨论导函数f′（x）的零点存在与零点分布情况往往是破题的关键.

例5已知函数f（x）=x2+ax+b，g（x）=ex（cx+d），若曲线y=f（x）和曲线y=g（x）都过点P（0，2），且在点P处有相同的切线y=4x+2.

（Ⅰ）略.

（Ⅱ）若x≥-2时，f（x）≤kg（x），求k的取值范围.

分析：构造辅助函数h（x）=kg（x）-f（x），问题转化为：探求函数h（x）在［-2，+∞）上的最小值，以及最小值非负时，参数k满足的条件.

因为h（0）≥0，所以k≥1.

求导得：h′（x）=（2x+4）（kex-1），令h′（x）=0，此时，我们可以解得：x1=-2，x2=-lnk.

下面，就只需要对x1、x2作大小关系的分类讨论，厘清函数h（x）的单调性，确定最小值即可.

（1）若x2＞x1，即1≤k＜e2时，

函数h（x）在［-2，-lnk）上单调递减，在（-lnk，+∞）上单调递增.

那么，h（x）min=h（-lnk）=-ln2k+2lnk≥0，

解得：1≤k＜e2.

（2）若x2≤x1，即k≥e2时，

函数h（x）在［-2，+∞）上单调单调递增.

那么，h（x）min=h（-2）≥0

解得：k=e2.综上所述，1≤k≤e2.

点评：本题的破题关键在于“解出导函数h′（x）的零点”，结合分类讨论，从而为确定函数的单调性、极值、最值奠定的基础.“函数恒成立”，具有一定的解题方向：“转化为函数的最值”.分析导函数f′（x）的零点存在与分布情况成为破题的关键点.G