发挥教材功效引领知识生长——一道课本习题的变式探究

☉浙江省嵊州市崇仁中学黄波平

发挥教材功效引领知识生长
——一道课本习题的变式探究

☉浙江省嵊州市崇仁中学黄波平

课本中的例、习题是高考命题的重要来源之一，每年的高考卷有不少试题是源于课本的，平时教学中不愿意挖掘教材中的习题，一味地在课外资料中挖洞，造成学生双基不牢.这启示我们平时复习要将回归课本落到实处.数学课本是数学知识、思想和方法的重要载体，又是教师和学生学习的主要依据，更是几代人智慧的结晶，具有较强的权威性、指导性、规范性.因此，高考命题高度关注课本在命题中的作用，充分发挥课本作为试题的来源功能.

分析：本题是“极坐标系与参数方程”中的一道练习题，借助曲线的参数方程可顺利解答.

解答本题也可借助解析几何问题的通法求解.

解法2：设M（m，n），B1（0，-b），B2（0，b），则直线MB1

点评：几何问题坐标化是处理圆锥曲线问题的重要途径，通过引入点的坐标、借助平面向量的计算，将几何问题转化为代数问题，从而使问题顺利求解.

一、改变问题的条件

例2如图1，已知椭D（0，-2）的直线l交椭圆于A、B两点，交x轴于点P，点A关于x轴的对称点为C，直线BC交x轴于点Q.

图1

（1）求椭圆的标准方程.

点评：本题将两个对称点的条件一般化，在解题过程中可将直线与椭圆方程联立，借助根与系数的关系整体求解.但要注意定值存在的条件，即k的范围.

二、变化所求结论

（1）求椭圆C的方程，并求点M的坐标（用m，n表示）；

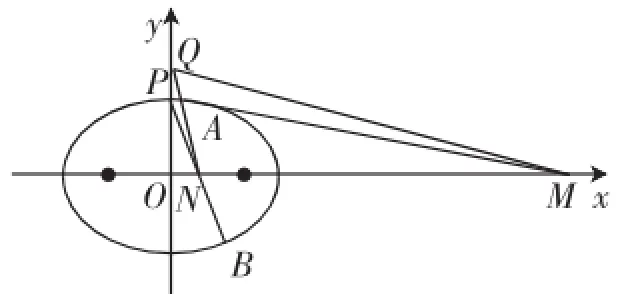
图2

（2）记点A关于x轴的对称点为B，直线PB交x轴于点N，问：y轴上是否存在点Q，使得∠OQM=∠ONQ？若存在，求出点Q的坐标；若不存在，说明理由.

（2）由题意知，B（m，-n），所以把点M坐标中的n换成-n，即得N设满足条件的点Q（0，t）（t≠0），由条件∠OQM=∠ONQ，得Rt△ONQ∽Rt△OQM，所以OQ2=OM·ON，即t2=；再由+n2=1，得t2=2.故存在满足题设条件的点Q的坐标为）或

点评：本题是例1和例2的拓展，本质上是选用两角的正切构建角相等的代数条件，但是题目中涉及两个相似的直角三角形，可以直接按比例建构对应的代数条件，更显简单直观.

三、改变问题的背景

（Ⅰ）当k=0时，分别求出曲线C在点M、N处的切线方程；

（Ⅱ）y轴上是否存在点P，使得当k变动时，总有∠OPM=∠OPN？说明理由.

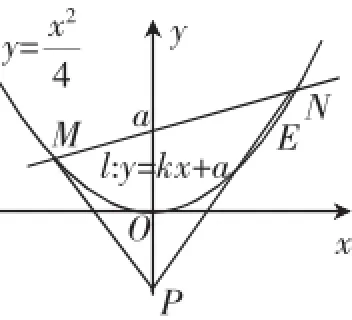
图3

点评：识别出题设条件∠OPM=∠OPN的本质是两条直线关于x轴对称.本题也可以按照斜率直接求出目标点：设所求点P（0，t），由k+k=0，得0，即PMPN2k+（a-t）·将根与系数的关系代入转化为2k+=0，即t=-a，故所求点为P（0，-a）.

“课本”是教与学的“根本”，高考作为选拔人才的考试，必然要以这个“根本”为依据，所以在平时的解题训练中应以课本为基础，在归纳课本的思想和方法的基础上，“拔高”课本，“变通”课本，使课本知识和思想方法得到升华.要做透课本中的典型例题和习题，要善于用联系的观点研究课本中的例题和习题，善于在高考题中寻找课本题的原型，在课本中寻找高考题的“身影”，探索高考试题与课本题目的交汇点，再将这些问题做恰当延伸或拓展，努力使课本知识更加丰富鲜活.F