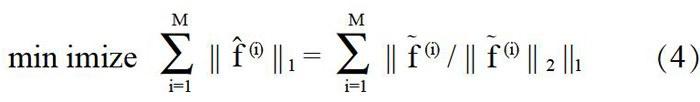基于稀疏滤波和神经网络的人脸识别算法

何金洋

[摘要]针对经典的主成分分析加距离测度人脸识别算法随着光照、角度、表情变化等干扰因素而出现的性能下降问题，从特征优化选择的角度。并结合神经网络非线性映射能力强、可以学习到数据局部分布特征的优点。论文提出了结合稀疏滤波和神经网络（SF-BPNN）的算法，该算法先采用稀疏滤波的特征竞争特质得到紧凑的初级特征表达，然后采用反向传播神经网络（BPNN）进行非线性分类，从而提高识别率。实验结果表明，论文提出的算法在较FERRET数据库下可取得较好的人脸识别效果。

[关键词]人脸识别；稀疏滤波；神经网络；SF-BPNN；主成分分析

1 引言

人脸识别是一种重要的目标识别技术。能够利用人脸图像的视觉特征来进行身份等信息的识别，发展前景十分广阔。由于在现实应用场景下，人脸姿态千差万别，外观的差异、物体遮挡、尺度、视角、所处背景环境不同以及光照等因素都会都对识别效果产生影响，许多方法或是过于依赖环境条件控制而不能达到现实场景下的识别精度，或是过于计算复杂而难以推广应用。

近年来，基于特征表达理论的人脸检测是一个富有潜力的研究方向，根据模型建立方式的不同，可以分为两种：一种是直接数据建模的方法：另一种就是避免直接建模，间接优化特征的方法。基于直接建模的方法具有较高识别率，但算法比较耗时，比如稀疏编码（sparseCoding，SC）算法需要花费很多时间来解L1范数最小二乘问题以找到稀疏系数。而另一类直接优化特征结构的方法就具有易于优化求解、计算简单快捷等优势，其主要代表是稀疏滤波算法（sparse Filtering，SF），它受稀疏编码思想的启发，强调特征优化后稀疏紧凑的特性，但采取了比前者简单的学习方式。

2 稀疏滤波SF特征

2.1 稀疏滤波算法

稀疏滤波的方法主要是绕过对数据分布的估计，直接分析优化特征的分布，通过优化L2范数归一化的特征激活值，加上L1范数的稀疏约束，直接分析优化特征的分布，只需调整一个参数（特征数目），并且可同时满足特征优化的三个条件：（1）种群稀疏（Populationsparsity），每个样本都只由有很少的非零特征来描述；（2）存在稀疏（Lifetime Sparsity），每个特征只在很少的样本中被激活；（3）高分散性（High Dispersal），所有的特征应具有相似的分布。算法原理：首先引入一个每一行是一个特征，每一列是一个样本的特征分布矩阵M。每个元素f_j^（i）表示第i个样本的第j个特征的激活值。接着计算线性特征：

f_j^（i）=w_j^Tx^（i）（1）

第一步，先对M的行进行归一化，再对列进行归一化，然后再将M中所有元素的绝对值求和。具体过程是先归一化每个特征为相等的激活值，将每一个特征除以其在所有样本的2范数：

（2）最优化高分散性

特征的高分散属性要求每个特征被恒等激活。在这里，可以直接地强制每个特征的激活值平方后的均值相等。在式（4）中，首先通过将每个特征除以它在所有样本的L2范数来归一化每个特征，使它们具有相同的如式（2）所示的激活值。实际上，它和约束每个特征具有相同的平方期望值有一样的效果：

因此，它已经隐含地优化了高分散性。

（3）最优化存在稀疏性

该算法的实验证明，对种群稀疏性和高分散性的优化就已经优化了特征的存在稀疏性。原因是：一个具有种群稀疏性的特征分布在特征矩阵里会存在很多非激活的元素（为0的元素），而且因为满足高分散性，这些零元素会近似均匀地分布在所有的特征里。因此，每一个特征必然会有一定数量的零元素，从而保证了存在稀疏性。

3 SF-BPNN特征

3.1 BP神经网络

误差反向传播神经网络（Back-PropagationNeuralNetworks，BPNNs）从结构上讲，是一种分层式的典型多层网络，具有输入层、隐含层和输出层，层与层之间多采用全连接的方式。同一层单元之间不存在相互连接。图1给出了一个典型的三层BP神经网络结构。

BP网络可被看成是一个从输入到输出的高度非线性映射，即F：R_m→R_n，Y=f（X）。对于样本集合：x_i（R_m）和y_i（R_n），可以认为存在某一种映射g，使g（x_i）=y_i，i=1，2，…，p。现要求有一个映射f，使得在某种意义下（通常是最小二乘意义下），f是g的最佳逼近。Hecht-Nielsen证明了如下的Kolmogorov定理：给定任一连续函数f：U→R，这里U是闭单位区间[0，1]，f可以精确地用一个3层前馈网络实现。

3.2 SF-BPNN特征

SF-BPNN特征由两步学习构成：首先，样本输入经过稀疏滤波，利用该算法产生特征竞争特效，得到降维的初级特征表达；然后，该初级特征被送入BP神经网络，进一步通过非线性函数映射来建立输入数据的内部分布模型，得到学习后的网络权值。在识别的时候同样先对测试输入样本进行稀疏滤波，再输入到训练好的BP网络之后就能得到直接具有分类效果的SF-BPNN特征。针对具体的一个人脸识别任务，SF-BPNN算法的流程示意图如图2所示。

4 实验结果与分析

在FERET人脸数据库上，使用PCA加各种距离测度作为基准，来跟单独应用的BP神经网络和本文的SF-BPNN算法进行比较。使用到的距离测度有斯皮尔曼距离（Spearman Distance）、城市街区距离（Cityblock Distance）和马氏距离（MahalanobisDistance），其计算公式如下表1所示。分别选择数据库里200人的1400张图、100人的700张图两种样本容量。每人的7幅图片里6张做训练。1张做测试。使用7折交叉验证取平均值的方法来计算识别率。首先使用PCA将数据集进行降维，分别保留95%、85%和75%的信息量，对应两种容量大小的样本集合，输入数据维数从6400维分别降低到了171维、28维和9维以及122维、24维和8维。然后将降维后的数据分别应用各种距离测度和BP神经网络来进行人脸识别。对于本文算法，先利用稀疏滤波将维数降低到跟PCA同等的数量，然后BP神经网络采用两个隐含层，第一个隐层120个神经元，神经元激活函数为tansig函数，第二个隐层40个神经元，激活函数为logsig函数。由于第一隐层采用的tansig函数值域为[-1，1]，所以先把输入数据映射到[-1，1]区间再作为网络输入。网络的训练方法采用量化共轭梯度法（Scaled Conjugate Gradient，SCG）或者是弹性BP算法（Resilient？Back Propagation，RPROP）。前面单独应用的BP网络跟这个使用相同的结构。这几种方法计算识别率之后作出如图3的对比图。各种方法的识别率列于表2。

说明：以上公式是假设给定m*n的数据矩阵x。可视为m个行向量x₁，x₂，…，x_m，两两行向量之间x_t和x_s之间的距离就被定义为d_st。

从图表可以直观地看出，常用的PCA加距离测度的算法不稳定，无法由统一的一种距离测度能在所有试验条件下都取得最高识别率。甚至有的距离测度在不同条件下识别率差异非常大，性能极不稳定。相比之下，神经网络的算法则性能比较稳定，识别率基本都保持在50%以上。由于在输入网络之前增加了稀疏滤波处理，可以去除许多无关甚至是干扰的信息。因此可以从结果看到本文提出的SF-BPNN算法将单独应用神经网络的识别率进一步提高了，并且即使滤波后特征维数只剩下9维也依旧把识别率保持在了60%以上。

5 结束语

本文提出了一种基于稀疏滤波的神经网络人脸识别算法，该算法利用良好表达特征应该具有的三种性质来进行特征稀疏优化。从实验结果上看，该算法的识别精度比PCA降维+距离测度的方法要高，也具有更稳定的性能。设计的两级级联特征提取网络在第一级快速优化特征，降低样本特征维数，得到选择后的初级特征。接着在第二级采用神经网络来建立输入数据的模型并直接输出指示类别的信号。并且在FERET人脸数据库上验证了此方法的有效性。