初中数学复习课的高效教学策略与建议

岑雪珍

步入初三，学生的学习任务随着学科数目的增多和数学学科综合性的增强，复习压力无形增大，那么初中的数学复习课如何实施呢？笔者认为复习课应该注重学生思维的引导和训练，为此尝试着利用思维导图来帮助学生优化初中数学的知识复习.

一、高效复习课的教学策略

1.借助于思维导图实施复习课的备课

每节课都要充分准备后才能和学生一起探究，对于初中数学的复习课也不能外.笔者认为在复习课的备课过程中应该借助于思维导图将教学目标、重点，以及难点统筹到教学设计中来，旨在让复习课的条理性更为清晰，帮助学生构建出更为清晰的知识网络，更好地应用知识解决与初中的数学知识相关的问题.

2.借助于思维导图组织复习课的教学

备课与课堂实施一脉相承，笔者认为课堂组织过程应该和备课的过程一样注重学生思维的程序性和知识的系统性.

（1）要求学生结合前面新课学习所得的数学概念、数学思想方法自主绘制出严谨的思维导图，思维导图凸显出所复习的章节的重点、难点，并以此为数学复习的中心有层次地发散，凸显出数学知识的层次性.

（2）在学生绘制思维导图的基础上进行讲解和二次探究，让学生展示出自己复习的思维过程，同时暴露出学生在复习过程中存在的知识和思维的缺陷，再以此为复习课的生长点让学生以学习小组为单位进行分析和讨论，从而实现对知识的认知更为完整，认识更为清晰，为顺利解决数学问题打下坚实的基础.

（3）在学生对知识全貌有所了解时，教师可以借助于多媒体或采用实物投影的方式将备课时预备的思维导图给学生看，然后有针对性地设置例题、习题，引导学生在习题分析和问题解决的过程中完成图式的联结，提高学生解决问题的能力和数学思维能力.

3.注重复习课后的反思

在初中阶段的数学学习过程中，学生会感到数学知识繁、杂，所以在复习课上必然存在知识及其应用过程中思维上的遗漏，所以课后，我们应该注重反思，教师通过对复习案例进行反思，弥补教学中存在的不足，从而提高教学质量.教师在实际教学的过程中进行反思，具有非常重要的意义，可以及时地发现教学中的不足，进而采取有效的措施进行改进，对学生进行有效的引导.

复习课后的反思除了教师的教学反思外，还有学生的复习的反思，学生反思自己复习过程中哪些知识还比较生疏，哪些方法的应用还比较生硬，自己在构建思维导图的过程中还有哪些缺陷和概念联系上的不足，便于完整的知识体系在头脑中构建，同时也便于学习方法和经验在头脑中沉淀下来.反思的过程是教师引导学生对数学概念和思维导图再认识和再探究的升华过程.

二、高效复习课的具体流程与案例

结合前面的分析，笔者将初中数学的高效复习课的课堂组织流程分为如下几个部分，下面结合具体的案例：“二次函数”的复习进行分析.二次函数这部分内容是中考的难点问题，如何高效复习值得思考与探究.笔者在具体的复习实践中进行了如下的安排：

1.设置开放型的问题情景，引导学生思维

在复习课的课前，要求学生对这部分内容自主预习，为了提高学生预习的实际效果，笔者设置了一个问题.

问题1 如图1所示，这是某一个函数的图象其中的一部分，请你注意观察，看一看能获取哪些信息？

设计意图 这个问题的起点设置比较低，但是出口很宽，学生能够联系到的知识点比较多，有助于本节内容的复习.

2.构建活动

学生前面对问题1进行自主思考，形成一定的认识，这些认识拿到复习课堂上来交流，继而形成对所复习知识的初步认识.

从学生反馈的信息来看，初浅的认识有如下几个：

信息1：这个函数的图象是开口向下，由此可知a<0；是轴对称图形，对称轴为：直线x=1（开口的方向和对称性）.

信息2：这个函数的图象经过（3，0）和（0，3）两个点（特殊点）.

信息3：从图形上看，当x=1，y对应着最大值4（最值）.

信息4：这个函数是二次函数，这个图象为抛物线.

深入一些的认识有如下几个：

信息5：我能判断这个函数为二次函数，那么其一般形式y=ax2+bx+c，这个函数的图象经过（0，3），很容易知道c=3.

信息6：对称轴为：直线x=1，可知x=-b2a=1，所以得到b>0.同时根据对称性，容易得到图象与x轴的另一个交点为（-1，0）.

信息7：根据图象信息可以借助于待定系数法来求函数的关系式，借助于顶点式得y=-（x-1）2+4；一般式得y=-x2+2x+3；交点式得y=-（x-3）（x+1）.

3.思维导图的第一次完善

从学生的认识和交流的情况来看，对基本知识和规律复习还是可以的，笔者再抛出几个问题，让学生的思维和认识能够第一次得以完善.

问题2：上面大家总结的方法很好，那么求二次函数的表达式的三种方法分别在什么时候用啊？

问题3：顶点式与一般式有什么内在的联系？

问题4：一元二次方程是否与二次函数也存在内在的联系？

通过前面的信息的提取与思考，加上后面这几个问题的解决，学生的思维导图出现了具有层次性的框架，层次有3：（1）对二次函数定义、三种形式的理解；（2）对二次函数的图象及其形式的理解（这是重点）；（3）对方程与函数关系的理解.

4.思维导图的再一次完善

为了进一步发展学生的思维，继续以问题的形式引导学生进行思考.

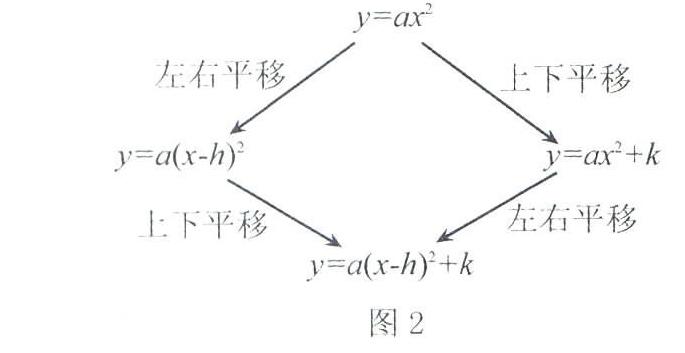
问题5：对于y=-（x-1）2+4的图象可以由怎样的函数图象平移得到呢？有多少种平移方式呢？

学生进一步讨论和归纳在原有思维导图的基础上加上第4个层次：（4）平移（具体图式如图2所示）.

5.典型例题训练

学生头脑中已经有了图式，接下来给学生提供例题，能够促进学生复习中知识的内化.

例题 二次函数y=ax2+bx+c和一次函数y=mx+n的图象如图3所示，若ax2+bx+c-（mx+n）=0，不解方程能写出根吗？

学生在解决这个例题的过程中实现了前面归结图式的应用，复习的实际效果也就最终落在了解决问题、检查和评价自己的复习成果中去了.

教无定法，对于复习课亦是如此，本文所涉及到的仅仅是笔者的一点实践体会与感悟，不当之处，还望专家同行雅正.