考虑学习行为的日常公交系统演化
曾鹦 侯爱华 李军
摘要:针对公交网络的特殊性,提出符合乘客路径选择行为的广义公交路径定义,考虑路段阻抗和站点阻抗,构建公交路径阻抗函数;基于经历-加权吸引模型,分析乘客的路径选择策略空间及路径吸引力更新规则,建立考虑学习行为的路径选择模型;从研究个体行为机制出发,探讨日常公交系统的演化过程,结合成都公交网络基础数据,运用模拟仿真实例诠释公交系统演化到广义用户最优均衡的过程,阐明城市公交系统的动态演化机理,为解释和预测乘客出行决策行为提供理论依据。
关键词:学习行为;系统演化;EWAL模型;路径选择;广义用户均衡
DOI:10.13956/j.ss.1001-8409.2016.08.29
中图分类号:U491 文献标识码:A 文章编号:1001-8409(2016)08-0133-06
引言
不管是实时信息作用,还是换乘行为影响以及乘客个体感知体现,现实生活中的公交出行,归根结底是一个动态演化过程:时变交通环境下,借鉴以往出行经验、参考当下实时信息对未来出行的路径阻抗进行预测,并据此调整出发时间或/和出行路径,将该过程称为乘客出行学习行为。考虑出行者学习能力对路径选择的影响在个体交通分配研究中并不罕见。早在1980年代中期,Horowitz等将以往出行成本的加权平均值作为当次出行路径选择依据探讨路径选择过程中的学习行为,但并未涉及出行者对出行成本的感知差异和信息影响[1]。近年来,以贝叶斯模型为基础的相关学习机制研究掀起了一股热潮,如Wen等在处理出行不确定性和出行者对信息获取及反应中有很好应用,但仅限于路径选择研究,不考虑出发时间和出行方式选择[2];国内外学者从换乘影响[3,4]、认知差异[5]、风险感知[6]、ATIS信息诱导[7-10]、风险规避[11]和可靠性[12-14]等角度对择路模型及配流模型进行扩展,分别建立了相应的路径选择模型和网络配流模型,但基于出行者完全理性假设且有充分把握获取和利用交通信息系统支持,与实际情况不太相符。显然,关于如何清晰合理刻画出行者的认知更新和路径选择行为在个体交通配流方面已成为一个新的研究热点[15, 16]。
然而,针对城市公交客流分配问题的研究大多都是对道路网个体交通分配的简单修正,其最大制约在于不能很好地反应和体现乘客路径选择行为决策规则,却又将其用之于不同个体不同出行行为下的公交网络,必然会产生与实际不符的分配结果,依此指导实践必然导致管理不科学。尽管文献[8]有所考虑,但针对乘客出行基于学习行为决策的选择机制对公交客流分配乃至整个公交系统演化尚缺乏内在机制研究。
本文基于行为科学理论,将经历—加权吸引学习模型用于乘客基于学习行为的路径选择建模,从建立个体行为机制出发,研究群体行为集计汇聚而展现出来的系统演化规律,阐明公交系统的动态演化机理,基于成都公交网络基础数据,运用仿真模拟算例诠释公交系统演化到广义用户最优均衡的过程,并探讨外界扰动对系统收敛或系统均衡的影响,为解释和预测乘客出行决策行为提供理论依据。
1公交网络基本描述
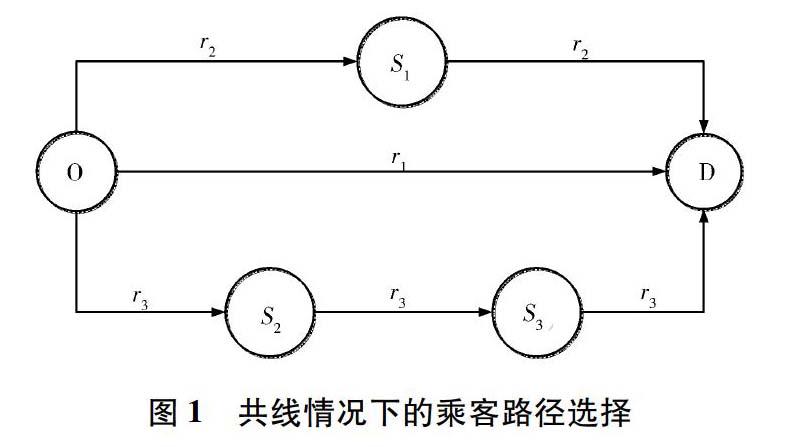
如图1所示公交网络,乘客可能选择直达路径r1,也有可能选择需要换乘1次的路径r2,在某些情况下甚至可能选择需要换乘2次的路径r3。部分起点站离出发地相对较近,部分终点站离目的地相对较近,部分站点可搭乘线路相对较多,这些均为影响乘客路径选择行为的关键因素。
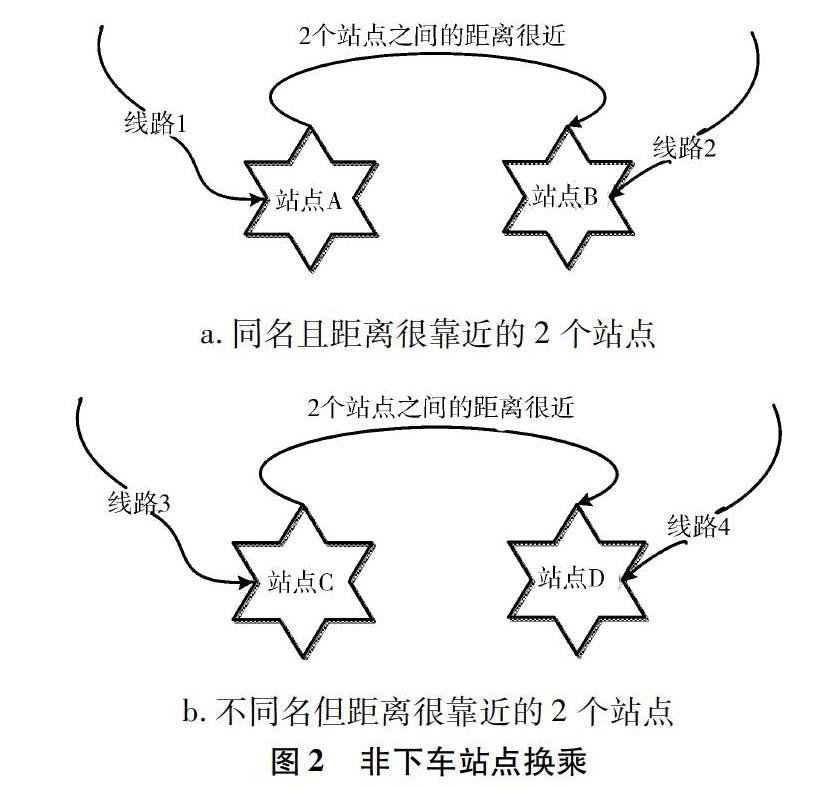
为避免降低可行换乘路径的搜索空间,综合考虑下车站点换乘(在下车站点即可搭乘需换乘的线路)和非下车站点换乘(乘客通过步行一段距离换乘的情况,见图2),将一定步行距离内可能换乘的多个站点抽象为一个换乘站点进行拓扑建模。定义符合乘客路径选择行为的广义公交路径为乘客从起点到终点所选换乘站点序列,简称路径(不管换乘与否,被选线路或线路组合均简称路径)。路径上相邻2个换乘站点之间的部分为公交路段(简称路段),路段通常包含一条或多条不同线路。简单公交网络与广义公交路径分别见图3和图4,原来7条线路编码的公交网络经由路径编码后,仅有3条路径即可清晰描述:途经站点s1和站点s4的路径r4,途经站点s1、站点s2和站点s4的路径r5,途经站点s1、站点s3和站点s4的路径r6。
2理论分析及建模
首先介绍经历-加权吸引学习模型的核心思想;接着分析经历-加权吸引学习模型用于公交出行决策的适用性;结合经历-加权吸引学习模型获取乘客路径选择概率;最后,以早高峰时段作为计量一个时期的基本单位,将乘客日常择路行为在时间轴上展开,阐述公交系统动态演化机理。
21经历-加权吸引学习模型
经历-加权吸引学习模型(Experience Weighted Attraction Learning,简写为EWAL)将强化学习和信念学习描述为特定选择模型参数的边缘情况,经验权重N(t)和吸引力值Ain(t)为EWAL模型的两个核心变量,二者通过经历加权公式N(t)=ρ·N(t-1)+1,t≥1和吸引值公式Ain(t)=φ·N(t-1)·Ain(t-1)+[δ+(1-δ)·I(cin,cn(t))]·πn(cin,c-n(t))/N(t)更新。
N(t):经历权重,可看成是对过去经历的“等价观测”;
Ain(t):t期策略r对决策者n的吸引;
cn(t):决策者n在t期实际选择的策略;
c-n(t):除n以外其他决策者在t期的策略;
πn(cin,c-n(t)):其他决策者在t期选择策略集合c-n(t)时,决策者n选择策略r的实际效用;
I(cin,cn(t)):关联指标函数,若决策者n在t期选择策略r,I(crn,cn(t))为1,否则为0;
ρ:经历权重贴现率,即上一期经历权重被记住概率;
φ:吸引贴现率,即上一期吸引被记住的概率;
δ:未被选中策略的效用权重,如果δ大于0,那么经验收集将扩大至未被选中的行动中,即个体可以通过观察未被选中的恰当行动进行学习。
Camerer等利用实验数据,通过极大似然法拟合这些参数,得出δ∈(05,1),φ∈(08,1)和ρ∈(0,φ)[17]。
整体而言,EWAL模型可视为一个强化学习模型框架进行理解:t期策略i对乘客n的吸引等于t-1期策略i对乘客n的吸引加上t期的期望效用,之后进行标准化。期望效用既包括选中的策略,也包括未选中策略。
22EWAL用于公交出行决策
EWAL模型首先被引入博弈领域,之后相继应用于其他领域[18, 19]。现实生活中的公交出行,不管是自己还是他人过去的成功出行经验,还是其他未被选择路径的机会成本,当这些信息均可用时,乘客都会加以考虑,而EWAL模型能恰到好处地综合考虑这些因素,赋予每条路径一个“吸引值”,用以表示乘客对该路径的偏好。
221路径阻抗
受发车频率、出行目的、出行时间、出行距离、出行费用、换乘方便与否等因素影响,乘客往往仅会考虑部分路径,称为有效路径。通过选取有效路径,将乘客为实现其物理位置转移而付出的时间和经济成本之和称为路径阻抗。因乘客对公交票价并不敏感,仅考虑时间成本计算路径阻抗。假设乘客未能搭乘吸引线路集中第一辆车,则一定能够搭乘第二辆车,或换乘其他公交线路,即不考虑二次等待现象。用usi(t)表示乘客在起点站或换乘站si等待吸引线路集中第一辆车的时间成本,则usi(t)=j/α°r∈Rwhr(t),当φ=05时,表示乘客到达服从均匀分布,公交车辆到达服从泊松分布,此时乘客等待时间服从均匀分布。
路径阻抗主要包括站点候车时间usi(t)和路段运行时间tsisj(t),因拥挤延迟导致乘客在起点站或换乘站si未能搭乘第一辆车的过载等待时间dsi(t)也不容忽视,当vsisj 222路径吸引力值更新规则 用Arn(t)表示乘客n第t天出行对路径r的偏好程度,各变量和参数均有其特定现实含义。 (1)经验权重N(t)表示乘客的出行经验积累值,用以衡量过去出行经验的重要程度,此处可理解为以往出行经验对乘客搜索当下可行路径的重要程度。 (2)πn(crn,c-n(t))表示其他乘客在第t天早高峰时段选择路径集合c-n(t)时,乘客n选择路径r的实际效用。 (3)关联指标函数I(crn,cn(t))取值根据乘客n在第t天早高峰时段选择的策略而定,当乘客n在第t天早高峰时段选择路径r时,I(crn,cn(t))为1,否则为0。 (4)相对于实际选择路径,乘客赋予未选路径的权重为δ,用以衡量选乘路径和未选乘路径的相对重要性,使得所有可行路径均有机会获得强化选择。 (5)吸引力值衰减系数,表示乘客对过去选择偏好的衰减程度。 (6)经历权重贴现率ρ,用以控制乘客对某一路径的偏好增长率。 223基于EWAL模型的路径选择行为 假设乘客对过去t期出行经历存有记忆,令Mr(1),Mr(2),...,Mr(t)为公交电子站牌显示“线路r距本站多少站”,tr(1),tr(2),...,tr(t)表示同一乘客在第1期至第t期参考电子站牌信息后经由路径r的实际通行时间,假设乘客在第1期对各路径出行阻抗一无所知,Mr(t)和M-r(t)分别表示第t期路径r和除路径r以外路径的电子站牌信息。令Urn(Mr(t),t)为乘客n结合以往出行经验于第t期获取信息后选择路径r的效用,有Urn(Mr(t),t)=V(Mr(t))+Arn(t)+ε成立。其中,V(Mr(t))为效用函数固定项,仅依赖于当天出行获得的电子站牌信息;Arn(t)为吸引力值,表示乘客n对路径r的决策偏好,可理解为乘客借鉴以往经验对路径r的信心,若该值为负则为排斥值;ε为误差项,用以表示乘客的认知偏差,假设ε相互独立且服从二重指数分布,则各路径选择概率Prn(t)可通过式(7)进行计算,乘客根据当期概率大小确定下一期的最优路径选择。其中,Prn(t)为乘客n在第t期选择路径r的概率,R为可供乘客选乘的有效路径数目,ω度量乘客对吸引力值变化的敏感程度。 23日常公交系统演化 时变交通环境下,乘客借鉴以往出行经验,参考当下实时信息对未来出行阻抗进行预测,并据此调整各自选择方案,将乘客日常择路行为在时间轴上展开,形成以下动态公交系统。 N(t)=ρ·N(t-1)+1, t≥1(1) Arn(t)=φ·N(t-1)·Arn(t-1)+[δ+(1-δ)·I(crn,cn(t))]·πn(crn,c-n(t))/N(t)(2) usi(t)=jα°r∈Rw hr(t)(3) dsi(t)=0vsisj ≥0vsisj=ksisj(4) πn(crn,c-n(t))=∑(usi(t)+dsi(t))·ηwrsi+∑tsisj(t)·λwrsisj(5) Urn(Mr(t),t)=V(Mr(t))+Arn(t)+ε(6)
Prn(t)=exp{-[Arn(t-1)+V(Mr(t-1))]/ω}∑k∈Rw,k≠rexp{-ω·[Akn(t-1)+V(Mk(t-1))]/ω}(7)
fwr(t)=qw·Prn(t)(8)
∑r∈Rwfwr(t)-qw=0(9)
xsisj(t)=∑w∈W∑r∈Rwfwr(t)·λwrsisj(10)
xsilm(t)=∑w∈W∑r∈Rwfwr(t)·λwrsisj·ηwrsi(11)
式(1)与式(2)为日常择路学习行为的基本原则;式(3)至式(5)为路径阻抗及对应的效用计算公式;式(6)为路径效用;式(7)为乘客基于学习行为的路径选择概率;式(8)与式(9)为流量守恒条件;式(10)与式(11)为客流量分配规则。
通常情况下,将公交网络中所有乘客出行选择都不再变化的状态称为系统均衡状态,该状态为理想状态下的收敛。给定一个可接受的容忍水平φ,当所有被选路径的最大吸引和最小吸引之差连续m天均不超过该容忍水平时,则认为该系统状态是收敛的[8],称该状态为广义用户最优均衡。
3应用算例
31基本状况描述
鉴于路径选择行为机制较复杂,难以从数学推理角度探讨公交系统演化的收敛性和收敛所需时间,运用图5所示简单公交网络,结合模拟仿真诠释公交系统的动态演化过程。
图5公交路网实例
从各公交站点出发到盐市口站,有48路和56路两条公交线路可供选择,二者的早高峰发车间隔(见表1),根据式(3)至式(5)计算各路径阻抗及对应效用(见表2)。
对成都公交卡的历史消费数据流量分析,56路选择比例明显高于48路,主要原因在于48路较56路绕行严重。
32结果与分析
由于成都公交只有上车刷卡记录,确切OD矩阵无从得知,故取早高峰时段搭乘56路和48路客流量均值作为图5中各站点到盐市口站的公交客流需求,令搭乘56路和48路的初始频率为05,表示乘客在初始阶段对这两条路径的选择偏好无明显差异。
(1)计算初始策略吸引值。构建似然函数,见式(12)。
L(An(0),ω)=∏n(∏Tt(Prn(t)))=∏n(∏Ttexpω·(Arn(t)+V(Mk(t)))∑2k=1expω·(Akn(t)+V(Mk(t))))(12)
(2)由路径初始吸引值需满足似然函数值最大,可得初始路径吸引值约束条件,见式(13)与式(14)。
exp(ω·(A56n(0)+V(M56(0))))exp(ω·(A48n(0)+V(M48(0))))+exp(ω·(A56n(0)+V(M56(0))))=05(13)
exp(ω·(A48n(0)+V(M48(0))))exp(ω·(A48n(0)+V(M48(0))))+exp(ω·(A56n(0)+V(M56(0))))=05(14)
(3)令48路初始吸引值为0,ω=01768,可得选乘56路初始吸引值为6191;借鉴文献[20],令ρ=092,φ=1,δ=076;因模拟中给定两条线路的初始选择比例均为05,此处令N(0)=1,表示当吸引值更新时给予初始吸引值及通过收益强化的量为相等权重;取容忍水平y=10,将初始值和各参数值代入式(2)和式(7),获得各路径流量变化(见图6)。受乘客出行学习行为影响,各路径流量从初期波动较大,逐渐趋于平缓,最终达到广义用户最优均衡状态。当r= 01时,系统收敛时间较长,r= 02时次之,当r3=03时,不同学习速度下系统收敛速度差异并不显著(见图7)。不同学习速度下56路客流量变化(见图8)。综上,公交系统相对稳定依赖于个体出行学习行为,但并不完全取决于它,主要原因在于公交线网布局和规划短期内很难变动,即便有变动,更多局限于现有线路的部分延长或某些线路的局部微调。
当系统达到图6所示均衡状态时,因外界扰动(如大面积道路修建引起48路绕行严重等)导致48路出行时间增加,使得当前稳定客流分布发生变化,初期并未产生很大影响,随着时间推移,乘客捕捉到该扰动,影响逐步扩大,一段时间后,系统再次达到新的均衡(见图9)。
综上,受乘客学习行为影响,个体乘客非合作情况下的公交出行终会达到广义用户均衡,学习速度不同将导致均衡所需时间各异。当达到均衡状态后,即便遭遇不可控干扰,系统终将达到新的均衡,说明公交系统具有较好的鲁棒稳定性。
33对比分析
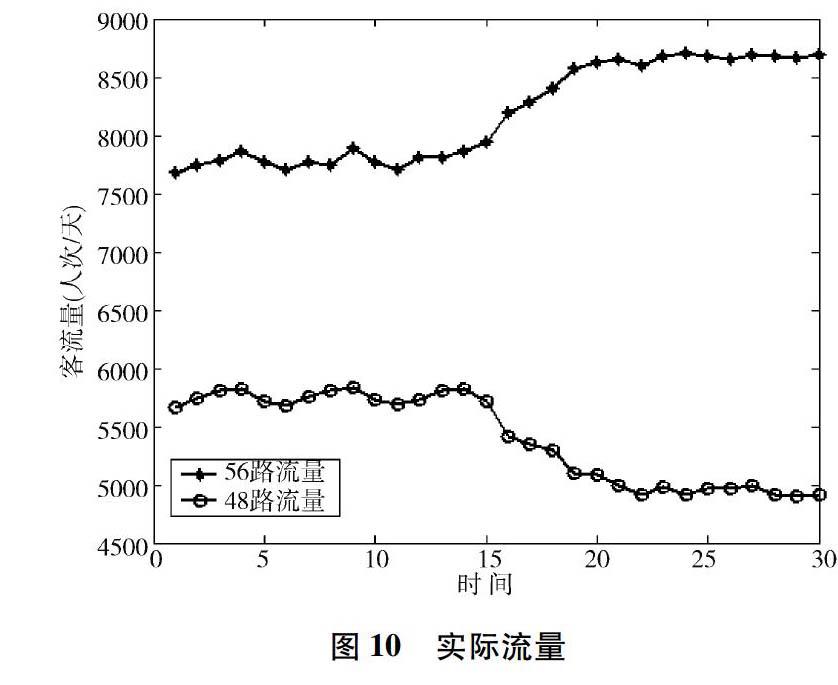
对比分析模拟结果与实际运营数据:以2012年3月15日二环高架修建(导致48路绕行而使其行驶时间增加)为时间界点,分析48路和56路这两条线路在此事件前后的实际流量变化,提取前后三周(排除双休日)48路和56路早高峰时段的刷卡数据,绘制两条线路的实际流量曲线(见图10),两条线路客流量在开建当天并未发生明显变化,一方面可能是乘客没有记清二环高架开建的具体时间,尽管各媒体有报道;另一方面,即便是知晓该事件发生,短时间内仍习惯之前的出行偏好,并未改变出行线路。
实际流量与模拟呈现的流量变化趋势相同:在二环高架修建之前,两条线路流量处于较平稳状态,修建之后的出行选择逐步有所变化:48路客流减少,56路客流增加,主要原因在于48路和56路共线明显,且二者均为承载上班族早高峰客流的重要线路。一段时间后,两条线路客流量逐步稳定,即模拟结果中所提到的新的均衡状态。
4结束语
类似个体交通出行,公交出行同样是一个不断收集路网信息、参考当下实时信息、借鉴以往出行经验进行学习的过程。基于EWAL模型探讨学习行为如何促进公交系统动态演化的内在机理,从分析微观个体乘客的路径选择行为机制出发,将乘客日常择路行为在时间轴上展开,构建时变交通环境下的动态公交系统,结合模拟仿真算例诠释公交系统动态演化过程。结果表明:EWAL模型为解释公交系统均衡提供了理论基础,能较有效、较充分地重现真实公交客流的宏观走向和规律,能更有效预测乘客出行决策行为。但模型的抽象化和实际问题的复杂化使得本研究尚有不足之处,若能比较精准地获取OD矩阵数据,如文献[21]提出的基于有序加权平均算子的公交线路OD矩阵估计进行对比分析是下一步需要进行的研究工作。
参考文献:
[1]Horowitz JL. TheStability of Stochastic Equilibrium in a Two-link Transportation Network[J]. Transportation Research Part B: Methodological, 1984, 18(1):13-28.
[2]T W K W, M GL. A Learning Model for Traffic Assignment: Incorporating Bayesian Inference within the Strategic User Equilibrium Model[J]. Australasian Transport Research Forum (ATRF), 37th. Sydney, New South Wales, Australia, 2015.
[3]徐光明, 史峰, 罗湘, 秦进. 基于策略均衡分配的公交线网规划优化方法[J]. 交通运输系统工程与信息, 2015, 15(3):140-145.
[4]曾鹦, 李军, 朱晖. 换乘行为影响下的城市公交配流算法[J]. 交通运输工程学报, 2013(4):70-78.
[5]彭昌溆, 周雪梅, 张道智,等. 基于乘客感知的公交服务质量影响因素分析[J]. 交通信息与安全, 2013, 31(4):40-44.
[6]E D. Urban Public Transportation Systems: Understanding the Impacts of Service Improvement Strategies on Service Reliability and Passengers Perception[D]. McGill University, 2015.
[7]张薇. ATIS 信息诱导下的路径选择行为研究[J]. 计算机工程与应用, 2013, 49(13): 234-236,257.
[8]Wahba MMAAL. MILATRAS:Microsimulation Learning-based Approach to Transit Assignment[D]. University of Toronto, 2008.
[9]巩亚文. 信息诱导条件下出行路径选择行为的演化博弈分析[J]. 公路, 2015, 60(1):108-113.
[10]杨智伟, 赵胜川, 张迅. 公共交通出行者 ATIS 信息选择行为影响因素研究[J].交通运输系统工程与信息, 2009, 9(3):29-35.
[11]刘天亮, 黄海军, 陈剑. 考虑风险规避和认知更新的日常择路行为演进[J]. 交通运输工程学报, 2008, 8(4):90-94.
[12]Szeto W, Jiang Y, Wong K, Solayappan M. Reliability-basedStochastic Transit Assignment with Capacity Constraints: Formulation and Solution Method[J]. Transportation Research Part C: Emerging Technologies, 2013, 35:286-304.
[13]Chen X, Yu L, Zhang Y, Guo J. Analyzing Urban Bus Service Reliability at the Stop, Route, and Network Levels[J]. Transportation Research Part A: Policy and Practice, 2009, 43(8):722-734.
[14]邵虎, 林兴强, 孟强. 基于出行时间可靠性的交通配流问题[J]. 管理科学学报, 2015, 12(5):27-35.
[15]高峰, 王明哲. 诱导信息下的路径选择行为模型[J]. 交通运输系统工程与信息, 2010, 10(6):64-69.
[16]Huang H, Liu T, Yang H. Modeling the Evolutions of Day-to-day Route Choice and Year-to-year ATIS Adoption with Stochastic User Equilibrium[J]. Journal of Advanced Transportation, 2008, 42(2):111-127.
[17]Camerer CF, Ho T-H, Chong J-K. Sophisticated Experience-weighted Attraction Learning and Strategic Teaching in Repeated Games[J]. Journal of Economic Theory, 2002, 104(1):137-188.
[18]Amaldoss W, Jain S, David vs. Goliath:An Analysis of Asymmetric Mixed-strategy Games and Experimental Evidence[J]. Management Science, 2002, 48(8):972-991.
[19]饶育蕾, 徐艳辉. 基于EWA博弈学习模型的股权分置改革对价均衡研究[J]. 中国管理科学,2008, 16(1):172-179.
[20]Viti F, Bogers E, Hoogendoorn S. Day-to-dayLearning under Uncertainty and with Information Provision: Model and Data Analysis[C]. In: The 16th International Symposium on Transportation and Traffic Theory, Maryland, US, 2005.
[21]彭建, 徐猛, 高自友. 基于有序加权平均算子的公交线路OD矩阵估计[J]. 管理科学学报, 2013(1):36-41,58.
(责任编辑:秦颖)

