基于翻转课堂模式下的高中数学微课设计

陈科钧

【摘要】 微课教学是一种新的教学模式，本文通过实例来谈谈在高中数学教学中的应用.

【关键词】 微课设计；翻转课堂；向量；立体几何

一、微课及其特点

（一）微课程的特点

微课创始人戴维彭罗斯认为，微课是一种知识挖掘的工具，可以作为知识脉冲，在相应的作业与讨论的支持下，可以取得与长时间授课相同的效果.胡铁生老师认为微课是指按照新课程标准及教学实践的要求，以教学视频为主要载体，反映教师在课堂教学过程中针对某一知识点或教学环节而开展教与学活动的各种教学资源的有机组合.

从微课的定义上看，微课具有以下的特点①时间短；②目标明确；③内容易懂.从微课设计的原则上看，微课设计具有聚焦性、碎片化与模块化、以学生为中心的特点

（二）数学微课的设计

随着我国学生在国际测试和竞赛中的不俗表现，许多学者对我国的数学教育经验进行了研究，“看重双基，强调熟练，要求严谨”已被大家所公认，但也有学者提出了其中的问题和不足，比如重结果、轻过程、重解答、轻反思、重教学设计、轻学生思维诊断等等.如何保留我国数学教育经验的精髓，克服其中的不足成为许多数学教育工作者研究探究的任务.新课标提出：“学生学习应当是一个生动活泼的、主动的和富有个性的过程”；目的是为了让学生参与到学习中，成为学习的主体.而翻转课堂教学模式中，学生可以课下看微课，完全做到个性化的学习，课堂上又可以通过合作交流，解决疑惑，在这个过程中，凸显学生的主体作用.

结合微课设计的原则及我国数学教育教学的特点，国内许多学者归纳了数学微课设计的四个步骤：①确定核心概念②设计微课结构③录制微课视频④设计使用指导

二、基于翻转课堂的高中微课设计与案例解析——以2015年宁波市优质课获奖作品“立体几何中的向量方法”为例

（一）“立体几何中的向量方法”微课设计分析

“立体几何中的向量方法”微课程是笔者参加2015年宁波市优质课评比的获奖作品.下面以该课程设计为例进行分析.

本案例选取人教版《数学》选修2-1的第三章第二节的内容，微课中包含了4个小视频：

1.用空间向量表示空间中的点、直线、平面；2.用空间向量来表示空间中的点、直线、平面的位置关系；3.用空间向量来表示空间角与距离；4.用向量方法与坐标方法解决立体几何问题.

（1）确定“立体几何中向量方法”的核心概念

通过分析，立体几何的基本元素是点、直线、平面；主要研究空间中点、直线、平面之间的关系及它们之间的角度与距离问题.空间向量作为一个工具去研究这些问题，故“立体几何中的向量方法”的核心概念是：向量表示点、直线、平面的位置（位置向量、方向向量、法向量）；向量表示点、直线、平面间的位置关系；向量表示空间角与空间距离；向量解决立体几何问题的“三步曲”

（2）“立体几何中的向量方法”的微课结构

（3）录制微课程

本节课的核心内容为利用空间向量解决立体几何的一般方法：先利用空间向量表示空间点、直线、平面等元素，建立图形与向量的关系；进行向量运算；由向量运算结果回归几何结论.可以通过类比平面向量解决平面几何的一般方法及通过例题讨论本节主题；故本案例采用PPT、几何画板、e板会；通过睿易通平台软件进行视频录制.通过几何画板和e板会通过运动的观点来进行研究，可以使学生对上述主题的认识进一步深化，提高抽象概括能力.

（4）设计微课自主学习单

本案例除了4个微视频外，支持资料还包括了系列课件，导学案、自测试卷等资料；引导学生使用资源，让学生带着问题观看微视频，然后进行测试，强化微课中学到的知识.

（二）案例一：用向量表示空间中的点、直线、平面的位置关系

1.设计思想

主要研究用向量表示空间中的点、直线、平面的位置及用向量表示它们之间的位置关系两个内容；通过提问链的方式，逐步探索本节课的主题；通过类比学习，由表示点的位置（位置向量）类比到表示直线的位置（方向向量）和平面的位置（法向量）；由简到繁，逐步探索.

2.学情分析

通过《数学》必修2中的立体几何和《数学》选修2-1的空间向量及其运算的学习，学生已具备一定的空间想象能力和代数运算能力，同时学生还具备用平面向量解决平面点、线位置关系的能力以及类比能力.但学生的数学思维能力还有所缺乏，认知结构还不健全，对向量和几何之间的综合运用还有所畏惧.

3.学习目标

理解利用向量表示点、直线、平面的位置，并且能用向量来判定直线、平面之间的位置关系（平行与垂直）；

4.教学过程

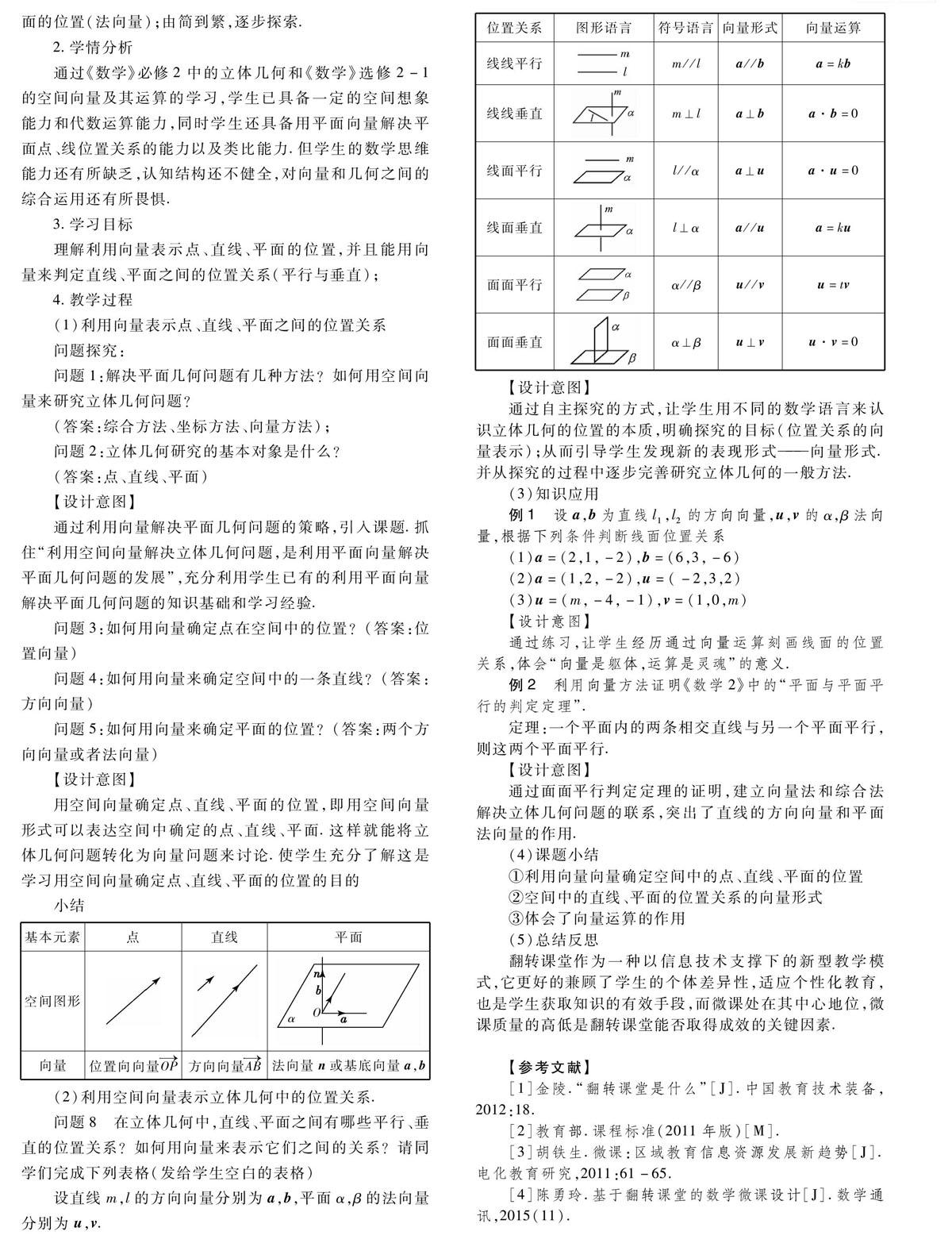
（1）利用向量表示点、直线、平面之间的位置关系

问题探究：

问题1：解决平面几何问题有几种方法？如何用空间向量来研究立体几何问题？

（答案：综合方法、坐标方法、向量方法）；

问题2：立体几何研究的基本对象是什么？

（答案：点、直线、平面）

【设计意图】

通过利用向量解决平面几何问题的策略，引入课题.抓住“利用空间向量解决立体几何问题，是利用平面向量解决平面几何问题的发展”，充分利用学生已有的利用平面向量解决平面几何问题的知识基础和学习经验.

问题3：如何用向量确定点在空间中的位置？（答案：位置向量）

问题4：如何用向量来确定空间中的一条直线？（答案：方向向量）

问题5：如何用向量来确定平面的位置？（答案：两个方向向量或者法向量）

【设计意图】

用空间向量确定点、直线、平面的位置，即用空间向量形式可以表达空间中确定的点、直线、平面.这样就能将立体几何问题转化为向量问题来讨论.使学生充分了解这是学习用空间向量确定点、直线、平面的位置的目的

小结

【设计意图】

通过练习，让学生经历通过向量运算刻画线面的位置关系，体会“向量是躯体，运算是灵魂”的意义.

例2 利用向量方法证明《数学2》中的“平面与平面平行的判定定理”.

定理：一个平面内的两条相交直线与另一个平面平行，则这两个平面平行.

【设计意图】

通过面面平行判定定理的证明，建立向量法和综合法解决立体几何问题的联系，突出了直线的方向向量和平面法向量的作用.

（4）课题小结

①利用向量向量确定空间中的点、直线、平面的位置

②空间中的直线、平面的位置关系的向量形式

③体会了向量运算的作用

（5）总结反思

翻转课堂作为一种以信息技术支撑下的新型教学模式，它更好的兼顾了学生的个体差异性，适应个性化教育，也是学生获取知识的有效手段，而微课处在其中心地位，微课质量的高低是翻转课堂能否取得成效的关键因素.

【参考文献】

[1] 金陵.“翻转课堂是什么”[J] .中国教育技术装备，2012：18.

[2] 教育部.课程标准（2011年版）[M] .

[3] 胡铁生.微课：区域教育信息资源发展新趋势[J] .电化教育研究，2011：61-65.

[4] 陈勇玲.基于翻转课堂的数学微课设计[J] .数学通讯，2015（11）.