向日葵也懂黄金分割

方百川

可是，向日葵的花朵中还蕴藏着数学之美，你知道吗？当你嗑瓜子的时候，你还能想起瓜子是怎样在那个大大的黄色圆盘上排列的吗？

在讲向日葵的数学之美之前，先请大家复习两个数学概念.第一个叫斐波那契数列，也叫兔子数列，它是这样的：1、1、2、3、5、8、13、21、34、55、89、144……还记得数学课上是怎么讲的吗？对，数列中每项是它前两项的和. 第二个概念叫黄金分割，即一个一分为二的整体，较大部分与整体的比值等于较小部分与较大部分的比值，这个比值约为0.618.请仔细观察兔子数列，如果用前一项除以后一项，即：1÷1=1，1÷2=0.5，2÷3=0.666…，3÷5=0.6，5÷8=0.625，……，55÷89=0.617977…，144÷233=0.61802…，……，46368÷75025=0.6180339886…，……不难发现，这个前一项除以后一项的值越来越逼近黄金分割的比值：0.618.

现在，我们再来观察向日葵，如下图：

图中，逆时针的白色螺线共有13条，顺时针的暗色螺线共有21条，13和21正是斐波那契数列中的两项.较大向日葵的逆顺螺线数目可以是（89，144），更大的甚至可以达到（144，233）.

后来，数学家们还发现向日葵圆盘中螺线的发散角是137.5°.我们知道，圆盘一周是360°，而360°-137.5°=222.5°，137.5°÷222.5°≈0.618，又是一个黄金分割.

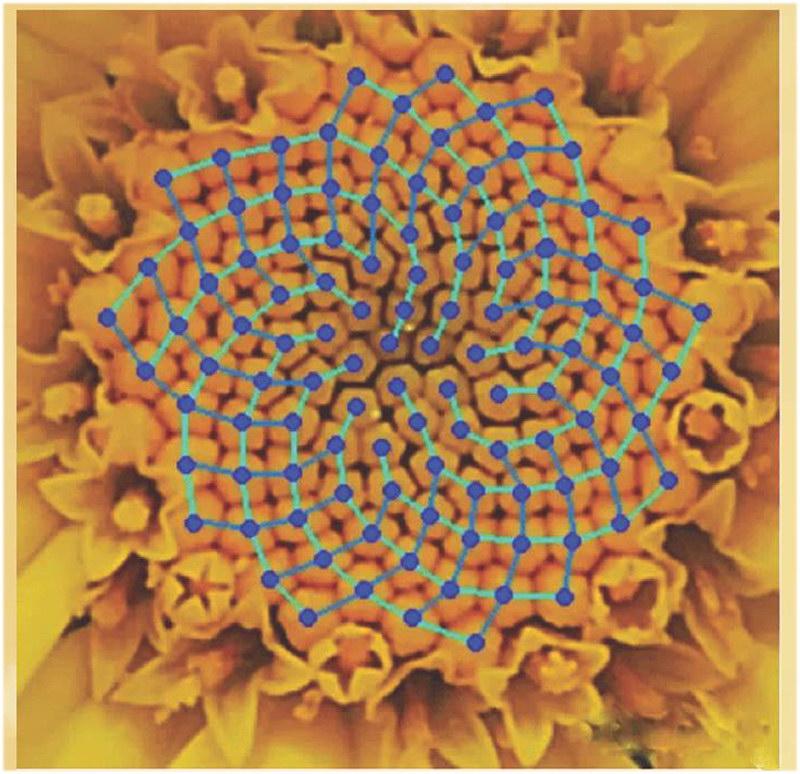
数学家在电脑上用圆点来代替葵花种子进行了模拟实验，如果发散角大于或者小于137.5°，圆点间都会出现间隙，因此，如果要使圆点排列没有间隙，发散角就必须是137.5°的黄金角，如右图所示：

对于向日葵来说，在有限的空间里开出足够多的花并结出足够多的种子是第一要务，在漫长的进化过程中，自然选择让向日葵有了可以用黄金分割来解释的数学之美.

（作者单位：江苏省扬州大学附属中学东部分校）