引转化思想之活水,显数学课堂之活力
冯双英
摘 要:研究转化思想如何在小学数学教学中渗透,教师通过从转化的角度去把握教材,能更好地把握教材的整体性、结构性。同时提高教师的有效性教学,诱发学生联想,将待解决的陌生问题通过转化,归结为一个比较熟悉的问题来解决。
关键词:转化思想;小学数学;课堂教学;渗透
一、将转化思想渗透在小学数学日常教学中
在探究转化思想在小学数学教学的渗透中,教师可从以下三个方面来进行:
(一)化繁为简,实现转化
1.条件转化
教师可以引导学生改变条件或问题呈现的方式,使那些复杂的隐蔽的条件关系变得清晰明朗,从而有利于解决问题。例如,教学“画三角形的高”时,教师可引导学生回忆过直线外一点画已知直线的垂线或垂直线段的方法。学生在黑板上演示画法后,教师在直线上截取了一段线段,将两个端点分别与直线外的那一点相连,并把多余的线擦去,便得到了一个三角形。
师:在三角形中,我们刚才画的这条垂直线段有一个特定的名称,请大家带着问题自学课本的内容,并和同桌交流。
生1:这条垂直线段叫做三角形的高,刚才截取的这条线段叫做三角形的底。
生2:我们可以把另外两条边(底边以外的两条边)先忽略不看,这样画高就成了从一个点(三角形的顶点)开始,画对边(底边)的垂直线段……听完他的发言,学生都露出了会心的微笑,果然,巩固练习时,学生画三角形的高的正确率较以往有了很大的提高。
2.等量转化
有些数学题给出了两个或两个以上未知数量之间的等量关系,要求这几个未知数,可以选择其中一个最基本的未知数量作为标准,通过等量代换,使题目的数量关系单一化。
例如:浙教版五年级上册中《菜市场采购》的教学片段,教师可这样设计:
甲买了2千克苹果、3千克梨,共付14.4元。乙买了4千克苹果、1千克梨,共付16.8元。(出示PPT课件)把问题情境列成两个等量关系:
甲:2千克苹果+3千克梨=14.4元 ①
乙:4千克苹果+1千克梨=16.8元 ②
将甲转化为:4千克苹果+6千克梨=28.8元 ③
③式-②式得:5千克梨=12元 即1千克梨=2.4元 ④
将④式代入①式得:1千克苹果=(14.4-2.4×3)÷2=3.6元
3.假设转化
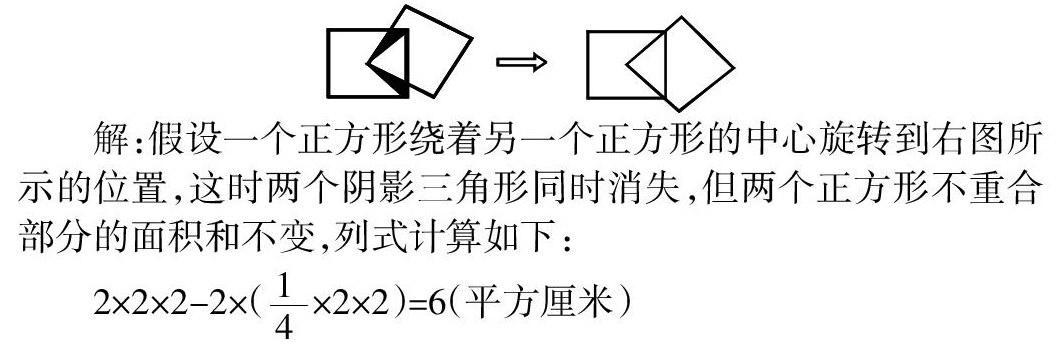
假设是一种重要的数学思想方法。假设法是先假定一种情况或结果,然后通过推导、验证来解决问题的方法。合理运用假设法,往往可以使问题化难为易,使解题另辟蹊径,有利于培养学生灵活的解题技能,发展学生的逻辑推理能力。例如,有两个边长是2厘米的正方形,其中一个正方形的顶点在另一个的中心上,并且两个阴影三角形的面积相等。问两个正方形不重合的面积的和是多少?
(二)化新为旧,实现转化
一般来说,基础知识越多,经验越丰富,学生学习知识时就越容易打通新旧知识的联系,完成未知向已知的转化。例如“除数是小数的除法”就是渗透转化思想的教材,教学中只要将除数是小数的转化为整数,问题就迎刃而解。据此教师可设计下面的教学片段:
(1)计算 36÷0.48
师:那36÷0.48列竖式又应如何来计算呢?
师:怎样把除数转化成整数呢?你们试着做一做。
问:被除数和除数同时扩大几倍是由谁来确定的?
(2)36.96英尺大约是多少米?1米≈3.3英尺
(3)说一说除数是小数的除法是如何计算的?
完成计算后,教师启发学生思考,使学生领悟到:除数是小数的除法是学生从未接触过的,看起来很难,但只要所学的知识与学过的知识整数除法沟通起来,运用转化的数学思想方法,把除数是小数的转化为整数,就能顺利解决问题。
(三)化曲为直,实现转化
圆的面积公式的推导,就要用到化曲为直的思考方法,通过将圆分割成若干等份,拼成近似的长方形,由圆的半径与面积的关系转化为长方形的长宽与面积的关系,由长方形的面积公式,推导出圆的面积公式。这里,就是将长方形的面积公式转化为圆的面积公式。在教学“圆面积公式”时,教师可这样设计教学片段:
师:我们学过了一些图形的面积计算公式,今天我们来研究圆的面积公式。你们有什么办法吗?
生:可以把圆转化为我们学过的图形。
师:怎么转化?
生:分一分。
演示把圆平均分成了2份,把两个半圆拼起来,结果还是一个圆。
生:多分几份试一试。
演示把一个圆分割为完全相同的小扇形,并试图拼成长方形。从平均分成4个、8个、到16个……
师:你们有什么发现?
生:分的份数越多,拼成的图形就越接近长方形。
生:圆的面积计算可以转化成接近长方形的面积来计算。
这个圆的面积公式的推导过程,是在学生有了前面“平行四边形的面积”推导前提下联想到转化思想。老师通过直观演示,让学生直观认识的基础上验证了公式推导的准确性。
二、以回望眼光,反思转化思想效果与体会
经过渗透转化思想教学的实践,深刻地感受到教师的教和学生的学之间一些质的变化。教师通过从转化的角度去把握教材的整体性、结构性,相互联系分析教材内容,这样在备课和教学中才能居高临下,有的放矢地进行教学。学生在感知、体验转化方法的过程中,对数学知识之间的联系能更深刻地认识。
转化思想方法的形成不是一朝一夕的事,它必须循序渐进反复训练,因此,教师应在不同内容的教学中反复渗透。必须自己不断地进行学习、进行尝试、进行总结,提高自身的教育理论水平和教学综合能力,当然教师也可以根据学生实际确定分阶段训练目标,使训练更具力度和效度。
参考文献:
[1]教育部.数学思想方法[M].中央广播电视大学出版社,2004-08.
[2]胡玲.以数学思想激发生命课堂活力的思考[J].扬州大学学报(高教研究版),2013(10).

