基于GARCH类模型的我国创业板市场风险度量比较

赵照++李保林

摘 要：以我国创业板指数为研究对象，在正态分布、t分布和GED分布假设下比较分析不同类型的GARCH模型，预测不同置信水平下收益率序列的VaR值，并对结果进行比较和检验，得出如下结论：尽管EGARCH和PARCH模型预测的VaR值比GARCH和TGARCH模型更加精确，但模型种类的选择并非VaR值度量的关键，而分布假设与显著性水平则是影响VaR值精确度的关键因素。在正态分布下，当置信水平较低时，估计的VaR值能较好地刻画收益序列的尾部特征，但当显著性水平很高（如99%）时，估计的VaR值存在低估风险的现象；在t-分布下估计的VaR值存在高估风险的现象；在GED分布下，无论显著性水平的高低，GARCH类模型均能很好地刻画收益序列的尾部特征。

关键词：创业板市场；在险值（VaR）；GARCH模型；后验测试

中图分类号：F830 文献标识码：A 文章编号：1003-3890（2016）03-0057-07

一、引言

创业板市场又称成长板、新市场等，是为自主创新企业和其他成长型创业企业的发展而设立的新市场。与主板市场相比，创业板以自主创新企业和其他成长型创业企业为主要服务对象，企业上市门槛较低，信息披露监管更严格，通常情况下创业板的成长性和市场风险均要高于主板。自2012年12月以来，创业板涨幅屡创新高，指数从585.44点持续上升到2015年6月5日的4 037.96点，成为投资者追捧的对象。但在创业板指数不断走高的同时，上市公司的业绩出现严重分化，在经济新常态下这种脱嵌式发展存在较大风险隐患。新常态背景下，随着资本市场的完善，股价的变动将逐渐反映公司经营的绩效，仅凭估值投资获取超额收益的时代将逐渐失效。民生证券（2015）梳理了近两年的创业板市场数据后发现，公司的净利润率与涨跌幅之间呈正相关，并且这种相关趋势在不断加强[1]。随着创业板市场规模的壮大，市场流动性不断增强，剧烈的波动使市场风险更加凸显，创业板市场风险的管理愈加成为金融监管部门以及投资者关注的重点。而风险管理的核心是风险的识别和度量，目前大多数学者选择采用基于波动率预测的GARCH模型来估算市场风险[2]。

GARCH模型是由Bollerslev（1986）在Engle（1982）提出的ARCH模型基础上发展而来。根据对方差方程的不同假设，形成了GARCH、EGARCH、GARCH-M和TARCH等不同类型的模型形式[3]。GARCH模型不仅可以很好的刻画金融时间序列的动态变化特征，而且可以对模型的波动性进行预测。作为预测VaR的一种主要的参数分析算法，GARCH模型在金融风险管理领域的实践中占据着重要的地位。Laurent和Peters（2002）[4]、Herzberg和Sibbertsen（2005）[5]等学者采用不同的GARCH模型对金融市场的在险值（VaR）进行了预测。陈守东、俞世典（2002）运用GARCH模型分析了我国沪、深交易所上市股票的风险，相较于正态分布，他们认为t-分布和GED分布可以更好地反映市场的收益特性[6]。王美今和王华（2002）对不同分布假定下的GARCH模型进行比较后认为，较之正态分布，t分布可以更好地对数据的厚尾性进行描述[7]。龚锐、陈仲常和杨栋锐（2005）基于正态、学生t及GED三种不同的分布假设，采用不同扩展形式的GARCH模型对上证指数、深证综指和上证180指数进行了对比分析[8]。徐炜、黄炎龙（2008）使用四种GARCH模型在三种不同的分布下分析了上证综指的VaR预测结果，结果发现，与正态分布和t分布相比，GED分布可以较好地反映上证收益率序列的厚尾特征，能够体现非对称效应的GARCH类模型在预测VaR值时表现更优[9-10]。

采用VaR方法预测的风险值通常跟收益率序列尾部的损益有关，计算VaR时需要提前假定时间序列所遵从的概率分布，考虑到大多数金融时间序列具有尖峰厚尾的特性，因此，大量的研究开始假定序列服从学生t分布或GED分布，但由于研究所选取的数据样本不同，分析的结论也不尽一致。本文在国内外研究文献的基础上，选取投资者较为熟悉和关注的创业板指数，采用GARCH、EGARCH、TARCH和PARCH等四种不同类型的模型，在正态、学生t和GED三种不同分布假设下，对收益数据进行拟合，并对估计结果进行比较和分析，从而更好地得出我国创业板市场收益分布的总体状况和风险特征，以及不同分布条件下各模型计算出的VaR值的精准度等，为不断发展的创业板市场提供合适的风险度量模型和决策依据。

二、VaR的计算与GARCH类模型

（一）VaR的计算

VaR（Value at Risk）是由J.P.Morgan最先提出的，通常是指在一定的置信水平下，资产或投资组合在未来某一时期可能遭受的最大损失。用公式表示为：

P（Δp>VaR）=1-c（1）

其中，c为置信水平，Δp为资产在持有期内的损失，VaR为在险值。VaR的计算通常涉及置信水平、资产收益的分布和持有期三个基本要素，运用参数法计算VaR值时概率分布的选择至关重要，由于实践中资产或组合收益率的概率分布较难确定，常见的做法是假定资产收益率服从正态分布，用GARCH模型来度量收益率的波动率。由此可根据上述（1）式，求得资产收益率在置信水平为c条件下的VaR值为：

VaRt=P0σZc■（2）

其中，P0表示资产的初始价值，σ表示标准差，Zc表示置信水平为c的下分位数，t表示资产持有期[8]。

（二）后验测试

后验测试主要是对估计得出的VaR值进行验证，最常用的是Kupiec（1995）提出的尾部损失频率测试，即把实际损失大于等于VaR值的频率与一定置信度下的上限值进行比较，以此来判断VaR模型的有效性。如果模型有效，则模型的尾部损失概率应该等于设定的置信度，即（1-c），如果尾部损失概率与设定的置信度（1-c）相差较大，则说明模型不合适[11]。假定实际考察的天数为T，失败天数为N，则失败率p=N/T，因此，失败率p为一个服从期望概率为p*的二项分布。零假设为p=p*，备择假设为p≠p*，通过检验失败频率是否拒绝零假设来评估VaR模型的准确性。Kupiec（1995）提出了采用似然比检验法对上述假设进行检验，他假定似然比方程为：

LR=2ln[（1-p）T-NPN]-2ln[（1-p*）T-NP*N]（3）

若零假设成立，则上述统计量LR服从χ2（1）分布。

（三）GARCH模型簇

广义自回归条件异方差（GARCH）模型是Bollerslev（1986）在Engle（1982）的自回归条件异方差（ARCH）模型基础上提出，通常由均值方程和条件方差方程组成。GARCH（p，q）模型的一般表达式为[12]：

rt=a0+■irt-i+μt

μt=σtξt

σ2t=ω+■αiμ2t-i+■βjσ2t-j（4）

其中，σ2t为条件方差，ξt为独立同分布的随机变量，ξt与σt相互独立，ξt为标准正态分布，p、q分别表示ARCH项和GARCH项的次数，并且？琢i、βi≥0。

GARCH模型通常用于资产收益率波动性的分析和预测，对金融市场的投资和决策具有指导意义。但资产价格的波动通常呈现出一种非对称性的特征，为了反映这种非对称性，Glasten et al（1993）在其1989年提出的GJR模型基础上，得出了门限自回归条件异方差模型（TARCH）[13]，其条件方差变为：

σ2t=ω+αμ2t-1+γμ2t-1dt-1+βσ2t-1（5）

模型中dt-1为虚拟变量，当μt-1≥0时，dt-1=1；当μt-1<0时，dt-1=1。γ为非对称参数，若γ≠0，则存在非对称效应。

同样是为了衡量资产波动的非对称性，Nelson（1991）提出了指数GARCH（EGARCH）模型，其假定条件方差的具体形式为：

lnσ2t=ω+■βilnσ2t-i+■■+γj■（6）

其中，γj表示价格冲击的非对称效应参数，若γj≠0，则存在非对称效应。从（6）式我们可看出，由于非对称项是指数形式的，它允许正和负的滞后值对波动性存在不同的影响，但条件方差本身一定是非负的[3]。

为了体现价格冲击对条件方差方程的影响，Ding et al（1993）提出了幂ARCH模型（PARCH），其条件方差方程为：

σtδ=ω+■βjlnσδt-j+■αi（εt-i-γiεt-i）δ（7）

其中，δ>0，当i≤r≤p时，γi≤1；当i

（四）关于分布假定

在计算VaR时，早期的研究大多假定模型残差服从正态分布，但正态分布不能较好地反映资产收益率的尖峰厚尾性，因此，Nelson（1991）、Hamilton（1994）等学者提出利用广义误差分布（GED）和学生t-分布来反映其尖峰厚尾特性[14]，其概率密度函数分别为：

f（x，v）=■exp-xν■ν/2（8）

f（x，v）=■1+■-（ν+1）/2（9）

其中，Γ（·）为Gamma函数，ν代表自由度，当ν→∞时，t-分布近似正态分布；当ν=2时，GED分布表现为正态分布。

三、实证分析

（一）样本数据的选取

本文以我国深圳证券交易所的创业板市场为研究对象，采用Eviews6.0和Matlab7.0软件对样本进行实证分析。由于我国创业板股票市场成立时间较晚，上市公司的数量和规模都较小，交易制度的不完善导致市场投机性较强，但深圳证券交易所自2010年6月1日起正式编制和发布的创业板指数可以更全面地反映创业板市场情况。因此，我们选取了2010年6月1日至2015年6月1日的创业板指数，共1 212个样本数据，采用自然对数收益率的形式，即：

rt=lnpt-lnpt-1

其中pt为创业板指数的t日收盘价；pt-1为创业板指数的t-1日收盘价。得到的结果如图1所示。

（二）数据基本特征分析

1. 数据的统计特征。图2统计结果表明，创业板指数日对数收益率的偏度为-0.316 4，峰度为3.815 0，J-B统计量为53.718 1，由此我们得出，创业板指数收益率序列不符合正态分布，存在明显的左偏，如图2所示。

2. 平稳性检验。创业板指数的日对数收益率序列在1%、5%和10%的显著性水平下均拒绝了“存在单位根”的原假设，因此，创业板指数日对数收益率为平稳序列，检验结果见表1。

3. 自相关性检验。从表2可以看出，创业板指数日对数收益率序列的自相关性并不显著，但高阶之后呈弱相关。

4. 异方差性检验。从图1可以看出，创业板指数日对数收益率序列的波动具有明显的波动聚集现象，通过对创业板指数日对数收益率进行LM异方差检验，结果见表3，从表中可看出，创业板指数日对数收益率序列存在条件异方差。

（三）GARCH族模型及VaR值的估计

通过对创业板指数日对数收益率的正态性、平稳性、自相关性和条件异方差性检验，我们初步判断创业板指数日对数收益率为存在异方差不存在自相关的平稳序列，因此我们设收益方程为一般的均值回归方程：rt=μ+σt，其中，μ为均值，σt为均值方程的残差。但其存在较明显的条件异方差特性，在建立GARCH族模型之前，用AIC信息准则反复测试，滞后阶数（p，q）为（1，1）时，AIC的取值最小，所以以下模型均为GARCH（1，1）类模型。

1. 正态分布假设下。从表4各参数估计的结果来看，在5%的显著性水平下各参数均较为显著。对上述模型估计的残差分别进行LM检验，结果发现异方差现象并不显著，因此上述四个模型均可以用来刻画创业板指数日对数收益率的异方差性[11]。同时，从参数γ和δ的估计值来看，创业板指数日对数收益率存在显著的非对称效应。

在上述模型估计结果的基础上，我们得到了各模型估计的VaR值及其统计特征和返回测试结果，如表5所示。

从表5可看出，在相同显著水平下，四类模型估计出的VaR最大值、最小值、均值和方差均无明显差异，GARCH模型预测的失败天数要大于其他三类模型。而在不同显著水平下，返回测试的结果存在明显的区别：在5%的显著性水平下，失败率均接近5%，并且LR统计量接受了VaR模型是正确的原假设，四种模型都通过了检验；在1%的显著水平下，失败率均明显大于1%，并且LR统计量拒绝了原假设，四种模型都未通过检验。因此我们认为，正态分布假设下，在5%的显著水平下，四种模型计算的VaR值结果比较准确，精度较高；在1%的显著性水平下，四种模型均被拒绝，说明越靠近左尾，其越难以反映市场的真实风险状况，并且存在过度低估风险的问题。

2. t-分布假设下。如表6所示，在5%的显著性水平下，上述参数估计的结果均较为显著，LM检验的结果显示估计残差的异方差效应并不显著，因此，上述各模型在t分布下依然可以较好地刻画创业板指数日对数收益率的异方差性。同时，从参数γ和δ的估计值来看，创业板指数存在明显的非对称效应。

基于t分布利用上述各模型估计的VaR值以及返回测试的结果如表7所示。

表7表明，在相同的显著性水平下，四种模型计算得到的VaR值较为接近。从返回测试的结果来看，同一模型在相同置信水平下，t-分布下估计的VaR值、失败率和失败天数均要小于正态分布。从LR统计量可知，无论显著性水平的高低，均拒绝原假设，四种模型都未能通过检验。所以可得出结论：t-分布假设下，四种模型计算的VaR值均过于保守，难以反映市场的真实风险状况。

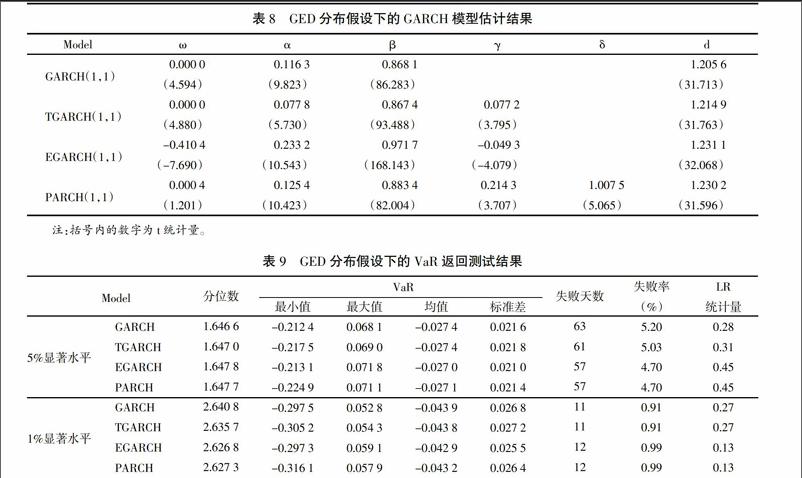
3. GED分布假设下。如表8所示，在5%的显著性水平下，上述各模型的参数估计结果均较为显著，LM检验结果显示各方程估计残差的异方差效应也不显著，因此，上述各模型在GED分布下也可以较好地刻画创业板指数日对数收益率序列的异方差性。此外，各模型估计的尾部参数在1.23上下波动，因此，相较于正态分布，GED分布可以更好地刻画创业板指数日对数收益率数据的厚尾特征。同时，从参数γ和δ的估计值来看，创业板指数日对数收益率存在显著的非对称杠杆效应。

利用上述各模型估计的VaR值的基本统计特征以及返回测试的结果如表9所示。

上述统计结果表明，在相同的显著性水平下，四种模型估计得到的VaR值较为接近，并且采用EGARCH（1，1）和PARCH（1，1）模型估计的VaR值标准差要小于GARCH（1，1）和TARCH（1，1）模型。从LR统计量可知，在1%和5%显著水平下模型均通过了检验。因此，我们可得出如下结论：在GED分布下，四类GARCH模型均能较好地对收益率序列的厚尾特征进行描述，并且可以给出较为精确的VaR值，与模型是否体现非对称效应的关系并不大。

四、结论

文章采用我国的创业板指数，运用不同类别GARCH模型，通过对比分析不同分布假设和显著性水平下计算的VaR值和返回测试结果，得出以下结论：

第一，在相同分布假设和相同的显著性水平下，四类GARCH模型计算得到的VaR值均较为接近，失败率和失败天数也相差不明显，采用EGARCH（1，1）和PARCH（1，1）模型估计的VaR标准差均略小于GARCH（1，1）和TGARCH（1，1）模型，但差距不大，从而说明模型种类的选择并非VaR值度量的关键因素。

第二，采用参数法估计VaR时，通常受到分布假设和显著性水平高低的影响。当对显著性水平要求较低时，正态分布和GED分布均可作为估计VaR的较好方法，但是当对显著性水平要求较高时，正态分布假设通常会低估风险值，而t-分布会高估风险值。无论显著水平高低，在GED分布下四类GARCH模型均能给出较为精确的VaR值。

第三，在相同GARCH模型和分布假设下，比较不同显著水平下的VaR结算结果，发现显著水平要求越高，得到的VaR值越小，标准差越大，并且考虑非对称效应的GARCH模型估计的VaR值标准差要小于不考虑非对称情况的GARCH模型，但结果并不显著，这也就说明VaR计算结果的精确性与模型是否体现非对称效应关系并不大。

以上结论将使我们更加清晰地认识我国创业板股票市场的风险特性，并为我国风险管理领域提供一个完善的技术解决方案。

参考文献：

[1]李隽.高换手率下创业板还能牛多久[N].第一财经日报，2015-05-13.

[2]陈林奋，王德全.基于GARCH模型及VaR方法的证券市场风险度量研究[J].工业技术经济，2009（11）：128-137.

[3]冯科，王德全.同业拆借利率的ARMA-GARCH模型及VaR度量研究[J].中央财经大学学报，2009（11）：36-40，46.

[4]LAURENT S，PETERSJ P.G@RCH 2.2：Anoxpackage for estimating and fore casting various ARC hmodels[J].Journal of Economic Surveys，2002，16（3）：447-485.

[5]HERZBERGM，SIBBERTSENP.Pricing of optionsunder different volatility models，Unpublished Manuscript，2005.

[6]陈守东，俞世典.基于GARCH模型的VaR方法对中国股市的分析[J].吉林大学社会科学学报，2002（4）：11-17.

[7]王美今，王华.基于GARCH-t的上海股票市场险值分析[J].数量经济技术经济研究，2002（3）：106-109.

[8]龚锐，陈仲常，杨栋锐.GARCH族模型计算中国股市在险价值（VaR）风险的比较研究与评述[J].数量经济技术经济研究，2005（7）：67-81，83.

[9]徐炜，黄炎龙.VaR-GARCH类模型在股市风险度量中的比较研究[J].统计与决策，2008（3）：20-23.

[10]徐炜，黄炎龙.GARCH模型与VaR的度量研究[J].数量经济技术经济研究，2008（1）：120-132.

[11]KUPIEC P. Techniques for verifying the accuracy of riskmea surement models[J].The Journalof Derivatives，1995，3（2）：73-84.

[12]BOLLERSLEV T. Generalized autoregressive conditional heteroscedasticity[J]. Journal of Econometrics，1986，31（2）：307-327.

[13]阿卜杜瓦力·艾百，李保林.我国交易所上市公司债宏观市场风险度量[J].金融教学与研究，2014（4）：50-53.

[14]黄光磊.不同分布条件下金融风险度（VaR）的GARCH/TARCH建模与实证分析[D].武汉：华中科技大学，2007.

责任编辑：高钟庭

China GEM Market Risk Measurement Model Based on Comparison of the GARCH

Zhao Zhao1，2，Li Baolin2

（1.Institute of Finance，Central University of Finance and Economics，Beijing 100081，China；

2.Yingda Asset Management Co.，LTD，Beijing 100020，China）

Abstract：As the research object，this article takes our country the GEM index in normal distribution，t-distribution and GED distribution assumption that comparative analysis of the different types of GARCH model，predict the VaR of yield sequence under different confidence level，and carries on the comparison to the results and inspection，the following conclusion：although PARCH and EGARCH model to predict the VaR than GARCH and TGARCH model is more accurate，but not VaR measurement model selection of the key factors，the key factors influencing the VaR measurement is distribution hypothesis and the level of significance. Under the normal distribution，when the confidence level is low，can well depict earnings estimates of VaR of the end of the sequence characteristics，but when significance level is very high （99%），estimates of VaR has the phenomenon of underpriced risk；Under the distribution of t-estimates of VaR value overestimate risk phenomenon；Under the GED distribution，regardless of the significance level of high and low，GARCH kind of model can well describe benefits of the end of the sequence features.

Key words：GEM market；Value at risk（VaR）；GARCH model；Acceptance test