一种新颖的小样本整体趋势扩散技术

朱宝，陈忠圣，余乐安（北京化工大学经济管理学院，北京 0009；北京化工大学信息科学与技术学院，北京 0009）



一种新颖的小样本整体趋势扩散技术

朱宝1，陈忠圣2，余乐安1
（1北京化工大学经济管理学院，北京 100029；2北京化工大学信息科学与技术学院，北京 100029）

摘要：基于数据驱动的生产过程建模、优化与控制是当今学术界与企业界的研究与应用热点。大数据时代小样本问题不可忽视。针对诸如人工神经网络（ANNs）、极限学习机（ELMs）等传统建模方法在小样本条件下难以获得较高的学习精度，提出了一种新颖的多分布整体趋势扩散技术（multi-distribution mega-trend-diffusion, MD-MTD）用于提升小样本学习精度。通过整体扩散技术推估小样本属性可接受范围，在整体趋势扩散的基础上，增加了均匀分布和三角分布描述小样本数据特性，生成虚拟样本，填补小样本数据点间的信息间隔。利用标准函数产生标准样本，在正交实验和不均匀样本实验下论证了MD-MTD的合理性和有效性，用MLCC和PTA两个实际的工业数据集进一步验证了MD-MTD的实用性。实验结果表明，MD-MTD能提高小样本学习精度8%以上。

关键词：小样本集；整体趋势扩散技术；虚拟样本；正交实验

2015-12-17收到初稿，2016-01-06收到修改稿。

联系人：余乐安。第一作者：朱宝（1987—），男，博士研究生。

引 言

现代石化生产过程系统应用了先进的控制系统和生产经营管理系统（DCS、FCS、MES、ERP、CRM、LIMS等），积累了大量有关生产过程的历史和当前生产的实时动态数据及企业经营管理等海量数据，但用于建模、优化与控制的数据需要覆盖整个过程系统运行的全范围，表征过程系统的整体特性，这就需要数据具有良好的分布性和一致性。正常运行状态下的数据相对平稳，不同原油的生产操作数据、开停车数据、历史故障数据等相对较少，常规的数据挖掘技术难于从稀少而弥贵的数据中挖掘出有效信息。人工神经网络、极限学习机和贝叶斯网络等传统学习工具广泛用于学习潜在知识，但当数据不充分时，这些学习工具性能差、泛化能力不足、鲁棒性不强，可能误导生产管理者的决策、管理与控制。机器学习的精度很大程度上取决于样本量的大小[1]，如何根据有限的、稀疏的、不充分的原始数据合理科学地扩大样本空间，强化学习工具的工作性能，成为人们解决小样本问题的切入点。

小样本学习问题不仅局限于统计学中样本数N少于50（工程上N取30）的样本学习问题，也包括数据挖掘中数据结构的不完整和不平衡问题[2-3]。由于小样本集在分布上呈现离散和松散的特点，数据间的信息间隔恶化了利用有限稀疏样本对总体特性的表征。小样本提供的信息是稀疏、离散的，由于信息间隔的存在，无法观测到观测点间隔间的信息。此外，小样本是总体的子集（如图1所示），直接通过小样本对总体特性进行推断是片面的和有偏的，不足为信。因此，撷取观测点间隔内的潜在信息对描述总体特征具有重要作用。

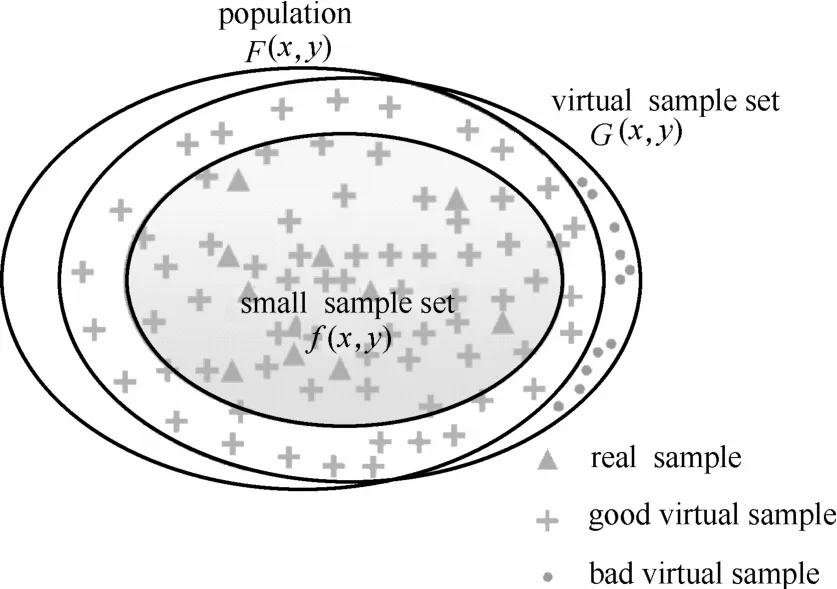
图1 总体、小样本、虚拟样本三者的关系Fig.1 Relationship among population, small-sample-sets and virtual datasets

目前，解决小样本集学习问题主要有两种思想。一种是基于灰色理论直接对原始的样本集进行建模[4-5]。另一种思想是生成虚拟样本，扩大样本的数量，富化小样本集的贫信息。虚拟样本的概念由Poggio等[6]首先提出，他们针对某个对象给定的三维视角，通过数学变换的方法，从其他任意角度生成新的图像，即虚拟样本，提高模式识别能力。虚拟样本的概念提出后，在加工制造业[5,7-10]、医疗[11-12]、图像处理[3,13]等领域得到广泛的应用。

为提高小样本学习精度，研究人员提出了功能虚拟总体FVP算法[7]、基于自适应网络的模糊推理系统ANFIS方法[8]、基于高斯分布的虚拟样本生成VSG方法[2]分别为小样本问题和不平衡数据问题开发的VSGGDS和VSGGDI算法、基于Bootstrap的虚拟样本生成方法[12,14]等。但FVP是对实际样本总体的有偏估计，特别是当系统的性能指标发生变化时，FVP可能会严重偏离实际样本总体且FVP没有被严格地理论证明；结合ANFIS的模糊化方法中采用对称性的扩散方式，没有考虑实际样本可能的非对称特性；基于高斯分布的VSG方法也没有提供有效确定均值与方差的方法；基于Bootstrap的虚拟样本生成方法执行有放回的重复抽样过程，仅对小样本集不同属性值进行组合，Bootstrap样本与原始样本特征完全相同，因而其学习性能实质上也只是对原始样本的重复训练而获得，并未撷取原始样本点信息间隔内所蕴含的信息。

模糊理论盛行后，模糊理论对填补信息间隔开辟了一个新的可行方向。Huang[15]基于模糊理论提出了信息扩散准则，导出了正态扩散函数，通过离散化的区间计算虚拟值填补信息间隔。Huang等[16]提出了扩散神经网络DNN，将信息扩散与传统的神经网络结合，用于函数学习。在给定某一发生的可能性下，DNN将数据点视为某一区间上模糊正态分布的数据中心，用对称的扩散函数对这些数据点进行左、右对称扩散。因此每个样本点可通过扩散得到两个虚拟样本点，利用虚拟样本增加的额外信息来获得更高的学习精度。DNN在一定程度上能填补由数据不完整性造成的信息空白，但没有指出如何确定扩散函数和扩散系数，与结合ANFIS的模糊化方法类似，DNN采用具有对称性的正态扩散函数并未考虑实际样本不对称的情况。此外，DNN要求变量间的相关性大于0.9，实际数据集很难满足这样苛刻的要求，大大限制了DNN的应用范围。

在Huang和Moraga的研究基础上，考虑到数据的整体性，Li等[9-10]提出了大趋势扩散技术MTD，将单点扩散推广到整体扩散，利用数据的趋势信息产生虚拟样本。但是，MTD及改进的MTD （TTD[1]和TBTD[10]）并未给出严格的理论证明。虽然MTD不需要原始数据的分布信息，克服样本对称扩大问题，但增加人工属性后，数据属性的个数是原始属性个数的2倍，由此扩大了BPNN网络规模，带来了高昂的计算开销和时间花费。同时，MTD采用三角分布来描述总体分布，形式过为简单，难以描述数据的特性。

针对基本MTD的上述缺陷，本文提出了一种新颖的多分布整体趋势扩散技术MD-MTD，通过多种方式验证了所提方法的有效性。

1 虚拟样本产生机制

在不同的研究领域，虚拟样本又称为合成样本[17]、人工样本[9-11,17]、模拟样本，但尚未形成虚拟样本的权威定义。下面给出虚拟样本定义。

定义1 令e=(x,f(x))表示随机训练集，其中x∈Rn。通过应用先验知识K，定义一种转换关系(T,yT)，生成原始样本集e的新样本(Tx,yTf(x))。yT到T的关系可能十分复杂，这取决于所研究问题的先验知识。这些新样本被称为虚拟样本。因此，给定训练集D={(x1,y1),…,(xn,yn)}，可通过合适的转换关系T产生虚拟样本集D′={(x′1,y′1),…,(x′n,y′n)}，其中x′i=Txi, y′i=yT(yi)Txi。

Niyogi等[13]从数学上证明了通过领域先验知识构造的虚拟样本能够像真实样本一样提供信息有效扩展训练集。

事实上多元线性回归（MLR）、神经网络（ANN）、支持向量机（SVM）、极限学习机（ELM）等监督式学习方法建立的预测模式（超平面）已经包含了样本属性间的关系，因此，可通过合适的监督式学习方法建立起总体（通常为存在但未知的）超平面和小样本集推估超平面，分别通过式（1）和式（2）决定。

2 MD-MTD工作流程

为了克服小样本下机器学习算法难以获得鲁棒的预测结果和优良的预测精度，MTD被用于估计小数据集属性可接受范围，填补信息间隔，计算虚拟样本值和隶属函数值（该样本值发生的可能性）。本文在基本的MTD基础上，提出了多分布整体趋势扩散技术（MD-MTD），如图2所示。

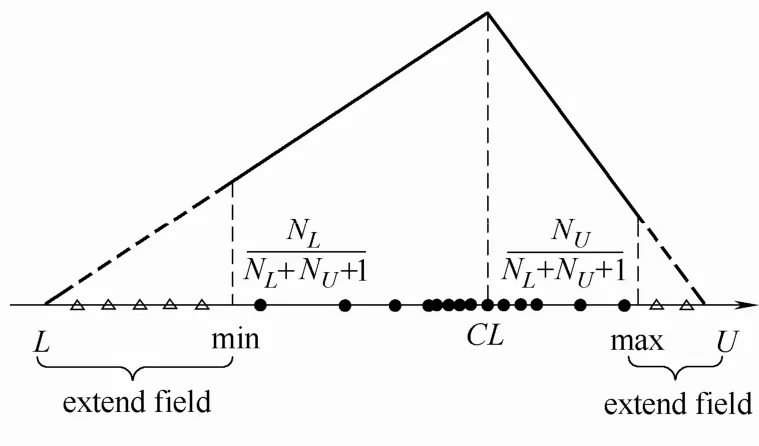
图2 多分布整体趋势扩散示意图Fig.2 Diagram of MD-MTD

2.1 多分布整体趋势扩散技术（MD-MTD）

给定样本集X={x1,x2,…,xn}，用基本的MTD估计X可接受边界，由式（3）、式（4）给出X的可接受范围下界L和上界U。

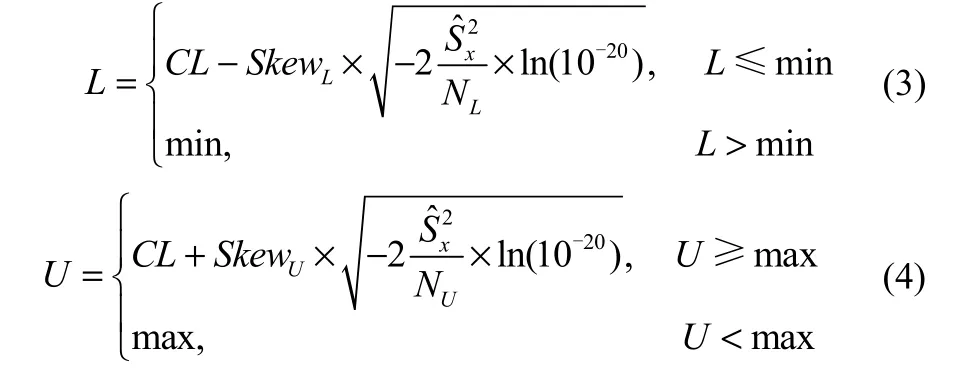
其中，

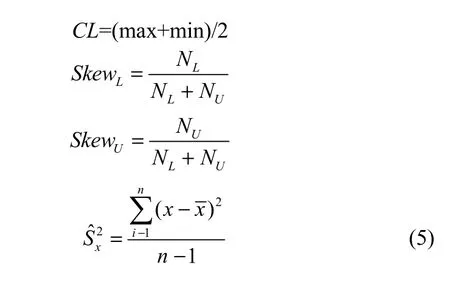
式中，n表示小样本集大小，CL表示数据中心，NL(NU)表示样本值小于（大于）CL的个数，表示小样本集方差，SkewL（SkewU）表示描述数据非对称扩散特征的左（右）偏度。

均值对离群点很敏感，为了更好地估计数据趋势中心且克服离群值对数据中心影响，将数据中心CL修正为

式中，x[·]表示顺序统计量。

由于离群点的存在，会使NL(NU)值偏大，因而造成对左（右）偏度SkewL（SkewU）的过高估计，致使过度增大数据推展域。因此在式（5）的SkewL、SkewU的计算式中，分母增加修正量因子m，防止出现数据推展域过度增大。将数据左偏度SkewL和右偏度SkewU修正为

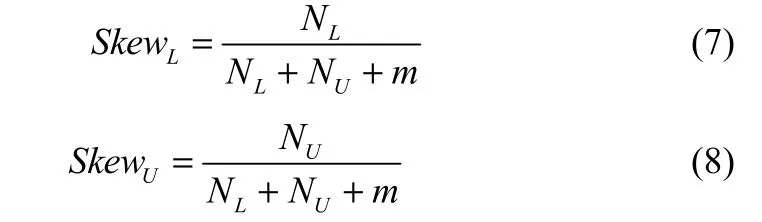
本研究中m=1。

样本集X的推展区域为[L,min]和[max,U]，直接观测区域为[min,max]。在推展区域[L,min]和[max,U]内，由于数据分布情况未知，因此用均匀分布产生虚拟样本点，在图2中用三角形空心点表示。在直接观测区域[min,max]，用三角分布描述数据分布情况，越靠近数据中心CL，数据发生的可能性越大，数据在分布上越集中；越远离数据中心CL，数据发生的可能性越小，数据在分布上越分散。在推展区域的虚拟样本点增加了额外信息，直接观测区域虚拟样本点填补了原始离散观测点的信息间隔。

通过MD-MTD过程，在信息上，扩展了原始样本集X的信息量；从训练上，有效增加了样本容量。在后面部分中将讨论MD-MTD提升小样本集的学习精度问题。

2.2 虚拟样本生成

对于给定的小样本集Ds=(x,y)，样本容量为Nreal，对任意输入属性xi，通过MD-MTD过程扩大输入样本容量。前面提到，监督式学习方法建立的预测模式（超平面）已经包含了样本属性间的关系。显然，采用生成与Ds的输入属性x相对应的y是合理的。文献[3]指出，当的平均绝对百分比误差MAPE不超过10%时，可用于生成与输入属性x相应的y。对于一般的学习工具，通过调整模型参数，容易保证MAPE≤10%。对于给定的Ds，虚拟样本生成可归纳为以下3个步骤：

① 采用MLR、ANN、SVM、ELM等监督式学习方法建立预测模式（超平面）；

② 对Ds的任意输入属性xi，通过MD-MTD过程产生所需数量Nvir的虚拟样本输入空间xvir；

由式(9)获得虚拟样本集Dvir=(xvir,yvir)，综合原始的小样本集Ds=(x,y)，最终得到样本容量为Nsyn=Nreal+Nvir的合成样本集Dsyn。

2.3 虚拟样本容量Nvir的确定

Nvir对最终预测模型的精度有直接的影响。就机器学习中的样本大小，计算学习理论努力寻找一个成功学习所需的训练样本数和计算量[12]，确定Nvir大小是小样本学习理论尚未解决的问题。总体来说，随着Nvir增大，生成的合理虚拟样本数就可能越多，最终获得的预测模型性能越好。但Nvir不合理增大也可能增加生成大量不合理虚拟样本数的可能，进而恶化最终获得的预测模型性能。本文通过采取多次改变Nvir大小来确定最合理的Nvir。

2.4 标准函数验证MD-MTD合理性和有效性

为了验证MD-MTD的合理性和有效性，定义一个3输入1输出的标准函数构造标准样本集，分别在正交和不均匀样本试验下，构造25个标准样本作为小样本集Ds，250个标准样本作为测试集Dtest。在本研究中，神经网络的激活函数为sigmoid函数，学习速率lr=0.01，动量因子mc=0.95，最大迭代次数epochs=5000，最大允许误差goal=1×10−8。

（1）正交实验

定义一个3输入1输出的标准函数

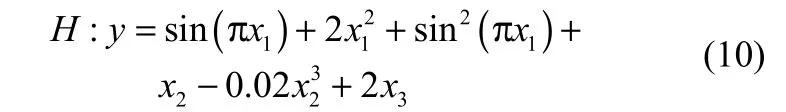
输入空间

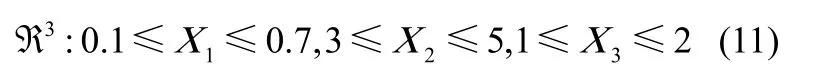
选用4位级或5位级的正交表进行样本选择，可满足足够的精度需求[18]。考虑到被引入的标准函数具有3个输入，因此选择3因素5位级的正交表L25(53)设计实验，进行均匀样本选择，得到25个正交样本作为小样本集Ds。3个输入变量（因素）5位级的线性离散取值

在定义的样本空间内，随机生成5000组样本，再从中随机选择250组作为Dtest，用3层BPNN和ELM进行建模验证。工作流程如下：

① 用BPNN/ELM对25个正交样本Ds建立小样本集推估平面，通过选择合适的节点数Nh（通常采用试误法来确定），确保MAPE≤10%。

② 设置Nvir=100，对任意输入x进行MD-MTD数据扩大过程，用计算相应的输出y=( x )，获得100组虚拟样本集Dvir，综合25组正交样本和100组虚拟样本获得125组合成样本集Dsyn作为最终的训练集。

③ 对Dsyn，用BPNN/ELM进行学习，用Dtest测试建立的BPNN/ELM预测模型，计算模型精度

④ 重复步骤②、③3次，计算MAPE的平均值

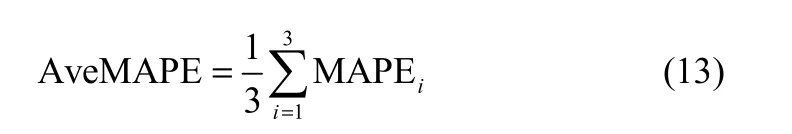
⑤ 重复步骤①～③5次，计算平均误差描述预测模型精度

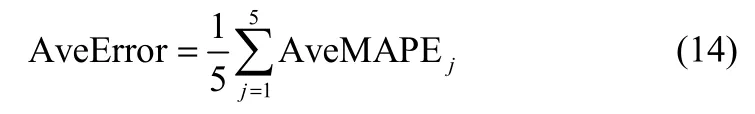
进行MD-MTD数据扩大前后，用BPNN和ELM学习测试结果如表1所示。用标准输出与预测输出的MAPE描述虚拟样本偏离标准样本的程度，虚拟样本偏离标准样本的程度取决于超平面的性能，与H越贴近，偏离（MAPE）越小，生成的虚拟样本越能反映总体的全貌。

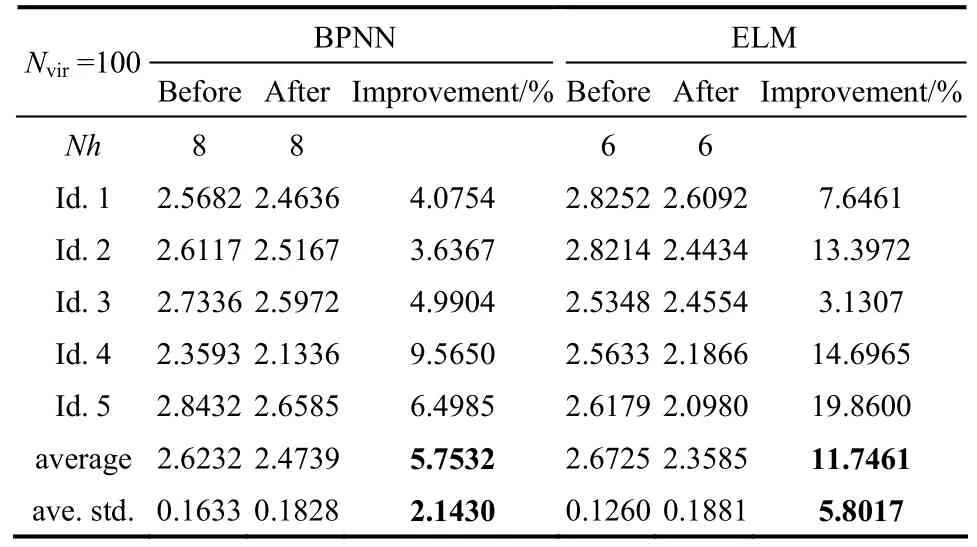
表1 25组正交样本在数据扩大前后精度变化Table 1 Accuracy variation before and after data extend with 25 orthogonal samples

由表1，进行MD-MTD数据扩大后，用BPNN 和ELM对Ds的学习精度对比数据扩大前都有明显的增加，BPNN的精度增量为5.7532%，ELM的精度增量高于BPNN的精度增量，达11.7461%，ELM的隐含层节点数6少于BPNN的隐含层节点数8，计算开销更小。5次独立运行后，BPNN的平均精度增量标准差为2.1430，ELM的平均精度增量标准差为5.8017，因而，BPNN的精度增量波动没有ELM的精度增量波动剧烈，＞比更贴近H，故的工作性能比的工作性能更加出色。因此，ELM的精度增量更高，但BPNN的标准差更小，即模型性能更稳定。

（2）不均匀样本实验

上述正交实验中，展示了MD-MTD能有效提高均匀分布的小样本集的学习精度。在实际生产实践中，获得实际样本往往在分布上难以呈现均匀性，通过不均匀样本实验验证MD-MTD的合理性和有效性更具实用意义。

为得到分布不均匀的小样本集，将3个输入属性在空间上均匀分成5个连续间隔，将标准函数的输入空间划分成5个区域。在区域1中，随机选取20组样本，在剩余区域中随机生成5组样本，构成一个样本容量为25的不均匀小样本集Ds，采用与正交实验中相同的测试集Dtest。

通过与正交实验类似的MD-MTD工作流程，用BPNN和ELM学习测试结果如表2所示。

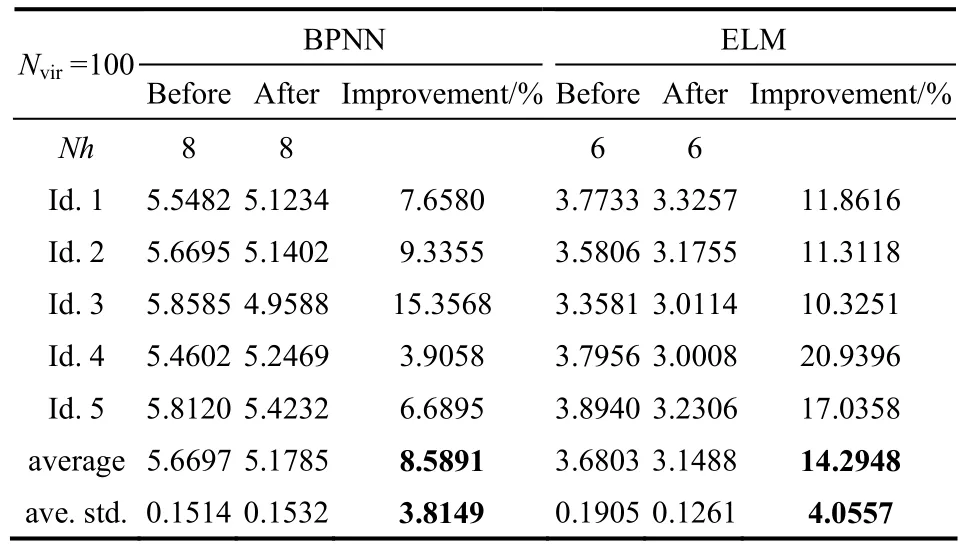
表2 25组不均匀样本在数据扩大前后精度变化Table 2 Accuracy variation before and after data extend with 25 inhomogeneous samples

通过表2可知，得到与正交实验一致的结论。在进行MD-MTD数据扩大后，用BPNN和ELM对Ds的学习精度对比数据扩大前都有明显的增加。ELM的精度增量高于BPNN的精度增量（分别为8.5891%、14.2948%），的工作性能比的工作性能更加出色，ELM的精度增量更高，但BPNN的标准差更小，即模型性能更稳定，ELM的节点数6少于BPNN的节点数8，计算开销更小。

3 实例研究

为进一步验证MD-MTD的实用性，下面对2个实际的工业数据集应用MD-MTD，结果显示，MD-MTD能提高小样本的学习精度在8%以上。

3.1 MLCC数据集应用

多层陶瓷电容器（multi-layer ceramic capacitors, MLCC）是陶瓷介电材料、相关辅助材料等精密化工材料和精细制备工艺相结合的高技术产品。MLCC数据集[3,10,12,14]包括比表面积（SA）、粒径大小分布90%分位点（PSD-90）、粒径大小分布50%分位点（PSD-50）等12个输入因数和1个输出（电解常数RK），共44组样本，随机选择30组样本作为小样本集Ds，剩余14组作为测试集Dtest。指定Nvir=100，按前述步骤用BPNN和ELM学习测试结果如表3所示。

表3 30组MLCC在样本数据扩大前后精度变化Table 3 Accuracy variation before and after data extend with 30 samples of MLCC

由表3可知，直接用BPNN或ELM对MLCC建立预测模型，模型的MAPE≥9%。经过MD-MTD，添加虚拟样本后，学习精度都得到改善，BPNN的MAPE在8.5%左右，其MAPE对比添加虚拟样本前提高了8.7%左右；ELM的MAPE在8.2%左右，其MAPE对比添加虚拟样本前提高11.5%左右。BPNN的MAPE增量幅度略低于ELM 的MAPE增量幅度，BPNN的MAPE增量波动比ELM的MAPE增量波动更平稳。ELM的节点数（Nh=18）少于BPNN的节点数（Nh=20），计算开销更小。

3.2 PTA数据集应用

精对苯二甲酸（purified terephthalic acid, PTA）是一种生产聚酯的重要化工原料。PTA数据集[19]共260组样本，包括进料量FC1501、温度TI1504、回流量FC1502等17个输入变量和一个输出（塔顶电导率），随机选择30组样本作为小样本集Ds，剩余14组作为测试集Dtest。指定Nvir=100，按前述步骤用BPNN和ELM学习测试结果如表4所示。

表4 30组PTA在样本数据扩大前后精度变化Table 4 Accuracy variation before and after data extend with 30 samples of PTA

表4显示了进行MD-MTD数据扩大前后，BPNN和ELM的MAPE变化情况。在进行MD-MTD前，BPNN和ELM的MAPE分别在0.84%、1.15%左右，在进行MD-MTD后，BPNN和ELM的MAPE分别在0.73%、1.03%左右，分别提高了12.31%、10.37%左右。BPNN的MAPE增量幅度略高于ELM 的MAPE增量幅度，BPNN的MAPE增量波动比ELM的MAPE增量波动更平稳。ELM的节点数（Nh=105）少于BPNN的节点数（Nh=120），计算开销更小。

4 结 论

小样本下机器学习算法难以获得鲁棒的预测结果和优良的预测精度。首先，本文通过提出的MD-MTD，结合MD-MTD与常规建模工具，形成了虚拟样本产生机制。其次，利用3输入1输出非线性标准函数产生的标准样本，在正交实验和不均匀样本实验下论证了MD-MTD的合理性和有效性。最后，通过MLCC和PTA实际工业数据集，验证MD-MTD的实用性和可靠性，结果表明，MD-MTD能提高小样本的学习精度在8%以上，在一定程度上改善了小样本学习精度。

References

[1] LIN Y S, LI D C. The generalized-trend-diffusion modeling algorithm for small data sets in the early stages of manufacturing systems [J]. European Journal of Operational Research, 2010, 207: 121-130.

[2] YANG J, YU X, XIE Z Q, et al. A novel virtual sample generation method based on Gaussian distribution [J]. Knowledge-Based Systems, 2011, 24: 740-748.

[3] LI D C, WEN I H. A genetic algorithm-based virtual sample generation technique to improve small data set learning [J]. Neurocomputing, 2014, 143: 222-230.

[4] LI D C, CHANG C J, CHEN C C, et al. A grey-based fitting coefficient to build a hybrid forecasting model for small data sets [J]. Applied Mathematical Modelling, 2012, 36: 5101-5108.

[5] CHANG C J, LI D C, HUANG Y H, et al. A novel gray forecasting model based on the box plot for small manufacturing data sets [J]. Applied Mathematics and Computation, 2015, 265: 400-408.

[6] POGGIO T, VETTER T. Recognition and structure from one 2D model view: observations on prototypes, object classes and symmetries [J]. Laboratory Massachusetts Institute of Technology, 1992, 1347: 1-25.

[7] LI D C, CHEN L S, LIN Y S. Using functional virtual population as assistance to learn scheduling knowledge in dynamic manufacturing environments [J]. International Journal of Production Research, 2003, 41: 4011-4024.

[8] LI D C, WU C S, TSAI T I, et al. Using mega-fuzzification and data trend estimation in small data set learning for early FMS scheduling knowledge [J]. Computers & Operations Research, 2006, 33(6): 1857-1869.

[9] LI D C, WU C S, TSAI T I, et al. Using mega-trend-diffusion and artificial samples in small data set learning for early flexible manufacturing system scheduling knowledge [J]. Computers & Operations Research, 2007, 34: 966-982.

[10] LI D C, CHEN C C, CHANG C J, et al. A tree-based-trend-diffusion prediction procedure for small sample sets in the early stages of manufacturing systems [J]. Expert Systems with Applications, 2012, 39: 1575-1581.

[11] LI D C, HSU H C, TSAI T I, et al. A new method to help diagnose cancers for small sample size [J]. Expert Systems with Applications, 2007, 33: 420-424.

[12] CHAO G Y, TSAI T I, LU T J, et al. A new approach to prediction of radiotherapy of bladder cancer cells in small dataset analysis [J]. Expert Systems with Applications, 2011, 38: 7963-7969.

[13] NIYOGI P, GIROSI F, POGGIO T. Incorporating prior information in machine learning by creating virtual examples [J]. Proc. IEEE, 1998, 86: 2196-2209.

[14] TSAI T I, LI D C. Utilize bootstrap in small data set learning for pilot run modeling of manufacturing systems [J]. Expert Systems with Applications, 2008, 35: 1293-1300.

[15] HUANG C F. Principle of information diffusion [J]. Fuzzy Sets and Systems, 1997, 91: 69-90.

[16] HUANG C F, MORAGA C. A diffusion-neural-network for learning from small samples [J]. International Journal of Approximate Reasoning, 2004, 35: 137-161.

[17] LI D C, LIN L S, PENG L J. Improving learning accuracy by using synthetic samples for small datasets with non-linear attribute dependency [J]. Decision Support Systems, 2014, 59: 286-295.

[18] 周毅, 徐柏龄. 神经网络中的正交设计法研究 [J]. 南京大学学报:自然科学版, 2001, 37(1): 72-78.

ZHOU Y, XU B L. Orthogonal method for training neural networks [J]. Journal of Nanjing Forestry University: Natural Sciences Edition, 2001, 37(1): 72-78.

[19] 贺彦林, 王晓, 朱群雄. 基于主成分分析-改进的极限学习机方法的精对苯二甲酸醋酸含量软测量 [J]. 控制理论与应用, 2015, 32(1): 80-85. DOI: 10.7641/CTA.2015.40398.

HE Y L, WANG X, ZHU Q X. Modeling of acetic acid content in purified terephthalic acid solvent column using principal component analysis based improved extreme learning machine [J]. Control Theory & Applications, 2015, 32(1): 80-85. DOI: 10.7641/CTA. 2015. 40398.

研究论文

Received date: 2015-12-17.

Foundation item: supported by the National Natural Science Foundation of China(71433001).

A novel mega-trend-diffusion for small sample

ZHU Bao1, CHEN Zhongsheng2, YU Le’an1
（1School of Economics and Management Science, Beijing University of Chemical Technology, Beijing 100029, China;2College of Information Science & Technology, Beijing University of Chemical Technology, Beijing 100029, China）

Abstract：Process modeling, optimization and control methods based on data-driven attract attention to both academic community and business circles in terms of its research domains and applications. Even in Big Data era, small sample problems cannot be ignored. In view of the difficulty of obtaining high learning accuracy with small-sample-set using traditional modeling methods, such as artificial neural networks (ANNs), extreme learning machine (ELMs), etc., a novel technology of multi-distribution mega-trend-diffusion (MD-MTD) is proposed to improve the learning accuracy of small-sample-set. The mega-trend-diffusion (MTD) is employed to estimate the acceptable range of the attribution of small sample. The uniform distribution and triangular distribution are added based on MTD to describe data characteristics, which are used to generate virtual samples and fill information gaps among observations in small sample. A benchmarking function is utilized to generate benchmarking samples under the orthogonal test and inhomogeneous sample test in order to verify the reasonability and effectiveness of the MD-MTD, and two industrial real-world datasets include MLCC and PTA are used to further confirm the practicability of the MD-MTD. The results of the validation tests manifest that the proposed MD-MTD can improve the learning accuracy of more than 8% for small sample.

Key words:small-sample-set; mega-trend-diffusion; virtual sample; orthogonal test

DOI：10.11949/j.issn.0438-1157.20151921

中图分类号：TP 181

文献标志码：A

文章编号：0438—1157（2016）03—0820—07

基金项目：国家自然科学基金项目（71433001）。

Corresponding author:Prof. YU Le’an, yulean@mail.buct.edu.cn