基于图像处理的物体质量与软硬度的测量

张学军，瞿祥和，雷锦添，毕红梅，刘天鹏

(1.广西大学计算机与电子信息学院， 广西南宁530004；2.广西多媒体通信与网络技术重点实验室培育基地， 广西南宁530004；3.广西高校多媒体通信与信息处理重点实验室， 广西南宁530004)



基于图像处理的物体质量与软硬度的测量

张学军1,2,3，瞿祥和1，雷锦添1，毕红梅1，刘天鹏1

(1.广西大学计算机与电子信息学院， 广西南宁530004；2.广西多媒体通信与网络技术重点实验室培育基地， 广西南宁530004；3.广西高校多媒体通信与信息处理重点实验室， 广西南宁530004)

摘要：物体的质量及软硬度的识别一般采用物理的方法来测量，操作复杂并且需要特定的工具，而对于物体内部则无法直接测量。随着机器人和计算机视觉技术的发展，利用图像处理的手段识别和分析物体的物理特性的研究成为可能。针对基于网格状的形变进行图像处理分析识别物体软硬度：在空间领域，采用薄板样条(TPS)算法对形变的最小弯曲能量值进行计算，对物体的柔软度进行量化分析；在频谱领域，采用傅里叶变换(FFT)算法计算出变形前后特征区域的频谱的变化值，寻找其与柔软度的关系曲线；将空间、频谱领域的实验结果整合分析，确定物体硬度的图像测定参数。物体所受作用力越大，产生的弯曲能量值越大，频谱扩散的效果越明显。针对一些柔软度较好的常见物体图像的实验效果进行对比分析，发现拉伸带的实验效果较好。对其施加不同大小的作用力，形变效果显著，且结果呈线性分布，符合理论预期。进而使用该测量方法对一组医学肝脏图像进行了分析，计量不同患者肝脏的柔软度，以帮助医生及时准确地诊断出肝纤维化程度，达到预防肝硬变及癌变的目的。

关键词：薄板样条;傅里叶变换;软硬度;频谱;弯曲能量;图像处理

0引言

对于人类而言，大约80%以上的信息来源于视觉[1]，其他通过触觉，听觉，味觉等来补充。虽然把视觉和触觉结合可以获取更多信息，对于机器人来说意味着需要更多的硬件传感器，增加了系统的复杂程度。随着图像处理技术的高速发展，机器人视觉技术的使用弥补了传感器(触觉)的不足。郝伟等[2]利用图像采集设备获取针织品图像，计算机视觉技术对针织品瑕疵区域进行定位，相比传统的光学仪器，自动在线检测能力和检测的准确性更高。安爱琴等[3]采用机器视觉自动分级苹果大小的方法，利用CCD摄像机获取苹果的样本图像，对样本图像的背景去除、二值化、图像平滑、特征量提取和图像标定等处理，参照苹果分级的国家标准完成了苹果自动分级,且分级精度高、速度快。物体的质量及弹性等特征的识别一般采用物理的方法来测量，如刘亚敏等[4]使用弯拉劲度模量来表征疲劳过程中试件的力学状态变化，通过控制应变的小梁疲劳试验，研究了沥青混合料疲劳过程中弯拉劲度模量随应变水平的变化情况，应变水平的变化模拟了实际路面厚度变化对层底拉应变的影响。李鹏博等[5]采用基于密度泛函理论的第一性原理计算方法来研究预测合金相的弹性性能和电子结构。利用应变和应变能的函数关系以及VRH近似法计算了弹性常数和弹性模量。这些测试操作复杂并且需要特定的工具，而对于物体内部则无法直接测量。目前为止的报道中采用图像处理的手段来测量和分析物体的质量和软硬度的研究还不多见。随着机器人和计算机视觉技术的发展，使利用图像处理的手段识别和分析物体的物理特性的研究成为可能。本研究采用不同于硬件解决方案的方法来检测柔软度较好的物体(如肝脏)的软硬度，主要基于计算机视觉技术来判断物体的硬度。

目前，利用CT或MRI设备对人体进行扫描成像，能够得出清晰的患者内部器官组织的医学图像，这极大地提高了医生诊断疾病的速度与准确度，降低误诊的可能性。肝癌是广西的高发病率疾病，而大多数原发性肝癌是由慢性肝病、肝硬化发展而来的，因此如何在临床上尽早发现并及时治疗这两种肝脏疾病成为挽救生命的关键。一直以来，肝纤维化的诊断是以穿刺病理活检作为金标准，但其为有创伤性的检查，也存在一定的并发症，患者不易接受，而且慢性肝炎时肝纤维化在肝脏中分布并不均匀，所以采用肝组织病理活检来评估肝纤维化的分期，可能存在样本误差，出现假阴性的结果。随着医学图像设备的发展，医学图像辅助诊断为医疗水平的提高做出了巨大贡献。但是,我国现阶段还基本上停留在医生通过肉眼观察影像来诊断受检者是否患有肝硬以及估计肝硬化的程度。对图像中所包含的大量复杂的信息,一些临床经验不足的医生一时难以做出正确的判断。即使是经验丰富的影像专家,单凭肉眼判断,也难免会由于疲劳等主观原因做出错误的诊断。

近年来，许多研究者利用灰度共生矩阵[6-7]分析肝脏影像图像的纹理特征量在肝纤维化[8-9]、肝硬化及结节状肝内占位性病变[10]等肝脏疾病的影像检测方面做了一些研究，肝硬化程度的图像处理研究逐渐成为热点。相对来说，对肝纤维化及肝硬化程度的一个重要指标——柔软度的研究比较少，主要原因是单从普通的CT或MRI图像上分辨不出肝脏的软硬程度的。本研究使用了带标签(Tag)信号的MRI图像对肝硬化程度进行量化研究。

笔者首先采用薄板样条(TPS)算法和傅里叶变换(FFT)算法从空间领域和频谱领域分别对相机获取的源图像进行大量实验并分析结果，寻找柔软度较好的材料如拉伸带作为人体肝脏的替代材料，作为前期阶段用来检验算法的正确性和软件平台的实用性。在取得较好的实验数据结果后，运用该软件平台对肝脏MRI的标签图像软硬度进行分析，得出正常肝脏和肝硬化的的分类曲线。该方法将进一步推动医学图像在肝脏硬度方面的研究，为肝脏的无创性检测带来福音，提高肝脏疾病的诊断效率。

1原理介绍和理论分析

1.1薄板样条算法原理

薄板样条(thin plate spline,TPS)。样条最初是指用长的柔性木条或金属条模拟船和飞机的表面，这些样条通过沿着它的长度附加不同的权重发生弯曲。类似地，同样可以将样条函数用于模拟图像的空间变换。基于特征点的图像变形方法，也就是薄板样条(TPS)变形算法，TPS实际上是一种插值方法。在这些点上,基于样条的变换不管是插值还是估计位移,需要将固定图像中的控制点映射到浮动图像的对应点。薄板样条函数插值实质上解决的是一个多变量插值问题[11]。在二维空间中，薄板样条函数插值的能量泛函为积分形式[12]为：

(1)

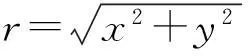
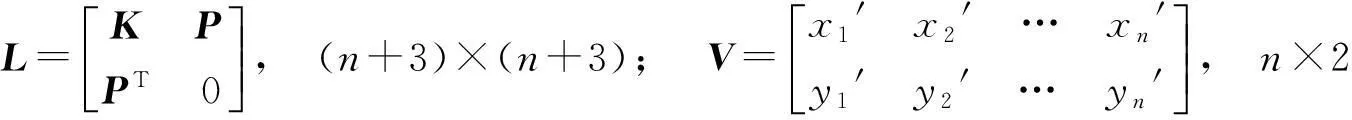
If=V(Ln-1KLn-1)VT。

(2)

1.2傅里叶变换

傅里叶变换就是将时域信号分解成众多不同频率的正弦信号或者余弦函数并叠加之后的和[13-14]。离散傅立叶变换是数字图像处理技术的重要工具，通过在时空域和频率域来回切换图像，对图像的信息特征进行提取和分析，简化了计算工作量，能看到在时空域所不能看到或者是不明显的一些特性。同时傅里叶函数也被喻为描述图像信息的第二种语言。特别是近些年来，随着医学的不断发展，很多医学领域都用到了大量的图像处理技术，其中的图像变换、图像分割、图像重建等在肝脏硬化的研究领域被大量的应用，而这些应用都涉及到了快速傅里叶变换算法。

1.2.1离散傅里叶变换(discretefouriertransform，DFT)

①一维离散傅里叶变换及反变换：

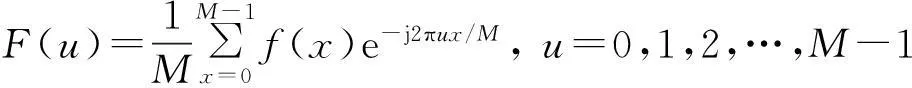
(3)

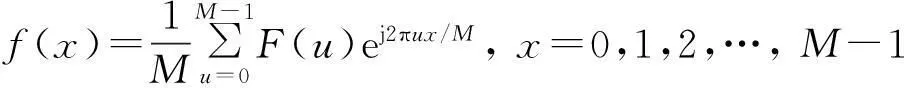
(4)

由欧拉公式 ejθ=cosθ+jsinθ， 则：

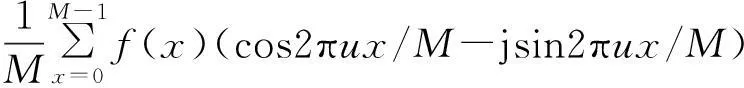
(5)

②二维离散傅里叶变换及反变换：

设M、N为正整数，则函数f(x,y)的DFT为：

(6)

式中u=0，1，2，…，M-1；v=0，1，2，…，N-1；u、v是频率变量，x、y是空域变量。若已知F(u,v)，则由傅里叶反变换可得f(x,y)：

(7)

式中x=0，1，2，…，M-1，y=0，1，2，…，N-1；u、v是频率变量，x、y是空域变量。

1.2.2快速傅里叶变换(FFT)

FFT是计算DFT的快速算法。DFT运算量巨大，运算时间很长。FFT的提出使得傅里叶变换的复杂度降低了很多，在很大程度上减少了计算量。 计算公式如下：

(8)

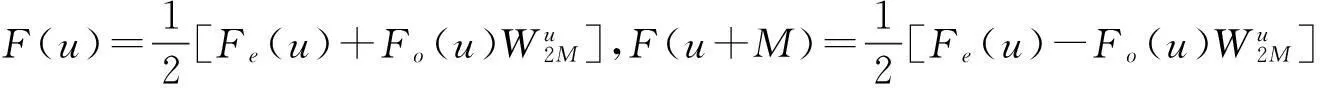
(9)

在本文的研究中，主要就是采用FFT的快速运算性能，用于计算频谱图像的功率谱值，并在程序运行结束后得出计算结果。

2实验方法与结果讨论

一个简便检测物体软硬程度的方法就是对物体施加一个外力，根据它在变形过程中产生的弯曲形变的程度来判断物体的硬度。一些柔软度大的物体在变形过程中其表面特征均会发生明显变化，通过肉眼就能够观测其变化。本研究的主要思路是针对图像特征点的变形进行定量化，找出形变量与物体质量和柔软度之间的关系。

2.1实验主要流程和材料

本文首先针对拉伸带上网格状的形变进行图像处理，使用空间领域和频谱领域的两种方法来分析物体质量。分别采用空域的薄板样条(TPS)算法和频域的FFT算法对形变的最小弯曲能量值和频谱扩散量进行计算，对物体的质量或硬度进行量化分析。实验测试系统的流程如图1所示：

图1　 质量和弹性测试系统流程图

在实验中，由于肝脏医学图像资源的短缺和相对单一，为扩大对物体软硬度研究的范围，笔者先寻找其他柔软度较好的替代材料，运用所开发的软件对多种初选材料进行实验验证。通过实验比较，最终选择的主要研究材料是柔软性较好的拉伸带[图2(a)]。其材料主体是橡胶，具有弹性好，易变形等特点。在拉伸带的下方悬挂一系列不同重量的砝码[图2(b)]。

(a) 拉伸带

(b) 砝码

图2 实验中使用的拉伸带和砝码材料

Fig.2Tensile belt weight sets using in our experiment

拉伸带中间打上红色标志点形成一个矩形形状[图3(a)]，图片网格点随不同砝码变化过程由相机拍下，可获取拉伸带处于不同拉伸程度时的图片[图3(b)～图3(d)]。

(a) 0 g　　　　　　　　　(b) 550 g　　　　　　　　(c) 1 200 g　　　　　　　　(d) 2 000 g

2.2空间领域实验

根据不同重量的砝码来拉伸物体所对应实验图片，可以看到标记点形成的矩形形状发生比较显著的变化,变形具有一定的路径连贯性[15]。笔者手动获取实验输入数据两组坐标值P和P′,P是0 g砝码对应的标记点坐标值，P′是其他重量砝码对应的标记点坐标值。把这些输入数据导入TPS最小弯曲能量值计算程序中，经过矩阵运算可以得出结果。

首先，测量一组粗略的数据(范围：50 g至1 000 g,增益为50 g)画出图4(a)。TPS最小弯曲变形能量值(即变形量)随着砝码重量的增大而增大，整体呈现上升的趋势，符合前面的设想。接着进行更详细的实验测量，给出其中两组数据图4(b)和图4(c)。

在图4(a)～图4(c)中，蓝色点是根据物体在不同的砝码重量的范围中计算得出的变形量画出的，黑色直线是数据分布的整体趋势线。它们实验数据的大小不同，是因为实验条件的改变，比如拍照的位置等。TPS变形量的计算结果表明：砝码重量越大变形量越大，并且基本上可以说是线性的关系，其中0 g砝码的变形量为0(即0变形的TPS变形量为0)。

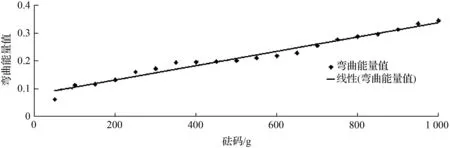
(a) 50～100 g,增量为50 g

(b) 0～2 000 g,增量为50 g

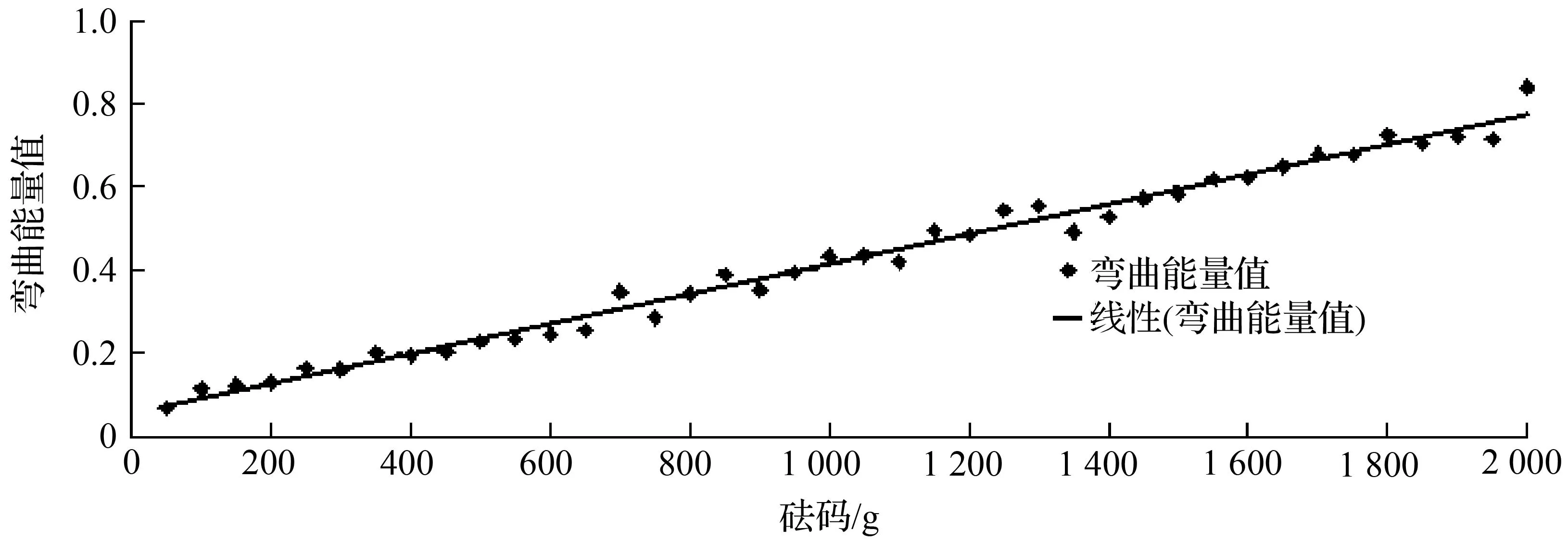
(c) 0～2 000 g,增量为50 g

2.3频谱领域实验

首先对图4的图片进行对比分析，把0 g重量砝码对应的图片导入程序中，对图片进行颜色提取，选取和记录下拉伸带上一定数量的红点和非红点处的灰度值(灰度值主要由三个量组成，即红、蓝、绿色)。其主要目的是根据拉伸带上红点和非红点处两个区域的灰度值对比，找出红点和非红点两个区域的各个灰度值分量的变化范围。通过前面的红点和非红点区域灰度值的统计分析之后，得出图片背景色的灰度阀值。根据得到的各个分量阀值对图片二值化，所有图片在相同的阀值条件下进行红点区域抽取，抽取所有的实验图片的目标区域，从而在实验中去掉图片的背景色(所谓背景色即主要为本次实验中的拉伸带的颜色)，仅仅留下实验材料上的红色标志点。在抽取特征点区域后，对抽取的区域所得到的图片进行压缩处理，使得原本较大的图片缩小为256×256，达到减少数据量来提高程序的处理速度的目的。最后进行傅里叶变换图片处理，计算频域中的频谱值。需要抽取红点标签点区域的主要原因：FFT分析实验时，可以在频谱图中去掉背景色的干扰因素，使得频谱图中仅仅留下目标区域的频谱变化，从而准确的得到实验的结果。否则FFT处理得到的频谱图是一片亮点，严重影响了实验结果的判断。频谱领域实验结果如图5所示。

(a) 0 g未处理背景(b) 0 g删除背景(c) 和300 g未处理背景(d) 300 g删除背景

图5加0 g和300 g砝码时未处理背景和删除背景的功率

Fig.5Spectrum images by o g and 300 g weight w/o background remouzl

通过对所有测量图片的FFT算法处理分析，从频谱图上可以看到，存在变化的主要是频谱图圆点(即频谱图的中心位置)，或者目标区域主要集中在圆点附近区域。同时本文研究谱图也不能仅仅关注圆点这一个点，或者是圆点周围的几个孤立的点，而是圆点附近一定范围区域的频谱值。因为本文要考虑到频谱扩散的影响因素，如果仅仅关注几个孤立的点，实验的精度和准确性将受到不小的影响。因此，本文在实验中选取了以圆点为圆心，三个像素单位长度为半径的圆形区域，在此范围中的所有的功率谱值(即频谱值)相加，使频谱扩散造成的影响最小。然后按照砝码重量从小到大的规律，分别统计出相应的频谱值总和，并画出相应的数据散点图进行分析。

相对应前面的空域实验，首先测量一组粗略的数据画出的数据图6(a)。由图6(a)可知，频谱值随着砝码重量值的增大而减小，整体呈现下降的趋势，和空域正好相反，符合理论的设想。通过进一步详细的实验测量，得出其中较好的一组数据见图6(b)。

(a) 0～2 000 g,增量为50 g

(b) 0～300 g,增量为50 g

通过数据分布散点图可以知道，随着砝码重量的增加，其特征区域的频谱值总和在不断的减小，这和预期的理论结果相符合，并且也基本上是线性的关系。不过与前面的空域实验正好相反，呈现下降的趋势。原因是频域范围内所讨论的是根据图像变化前后点的大小来判断形变情况的，在物体受到压迫向另一个方向运动后，其表面的标记点会变小，从而造成实验数据即功率谱和值的下降。总体而言就是物体在受到一定的力的作用之后，其将发生形变，而受力一定时，根据形变的大小就可以判断出其软硬度，但在频域中能更加详细地观察到形变的具体细节。图(4)和图(5)实验数据的大小范围不同，是因为后面根据具体情况只选取前面的一半特征点进行处理。

2.4两种实验方法的分析和比较

在以上两种实验方法得出的结果中，笔者将进行实验结果的验证，以讨论此方法的正确性和可行性。在实验后，根据前面得出的实验结果直线关系，理论质量和实际质量进行对比，并算出两者的偏差比，即偏差比=(理论值-实际值)/实际值。偏差比越小说明实验结果的正确性和可行性越高。

①时域实验：沿用上述获取实验图像的方法获取两组图像，合并两组图像所得结果求得散点，如图7所示。

图7　空域实验数据分布图

蓝色数据点是根据物体在0～2 000 g的范围中由两组不同的数据合并后取平均值而得出，黑色直线是数据点分布的趋势线。根据趋势线上的点可求得直线的数学表达式为y=0.000 375x ；以图7中的数据为已知条件，根据式(2)反过来求出砝码质量，得出数据结果记录如表1所示。表1中的数据结果求得砝码质量的偏差，平均偏差值比为3.27%，砝码质量偏差值较小。

②频域实验：频域实验方法和空域实验部分的类似，得出数据分析见图8所示。

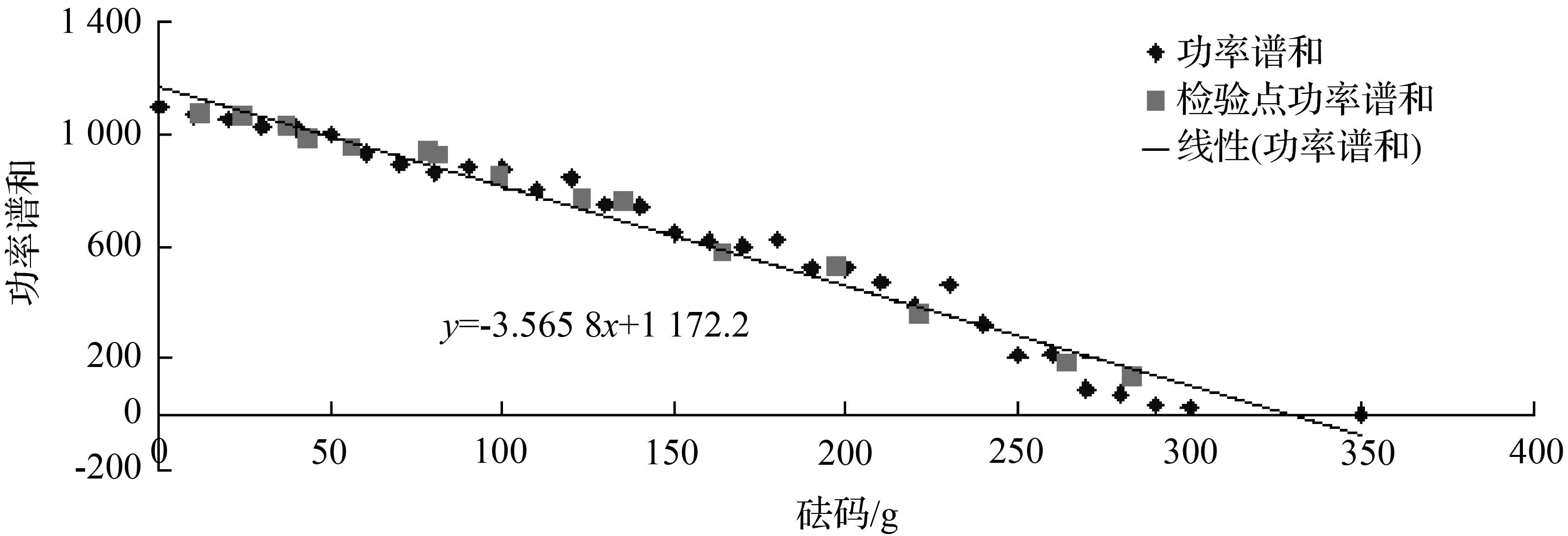
图8　频域实验数据分布图

频域实验的平均偏差值比为0.01%。

表1　砝码质量的实验偏差

综上所述，与时域方程保留一致可以得到结论：在空间上，物体的软硬度与TPS最小弯曲能量值成线性正比的关系，即物体的形变越大能量值越大；在频谱上，物体的软硬度与FFT频谱图的中心区域的频谱值的和成线性反比关系，物体的形变越大频谱值越小，与前面正好相反。表明采用TPS算法和FFT算法从空间领域和频谱领域可确定拉伸带的软硬度，并且所得效果较好，此法可扩展应用于其他物体的软硬度检测。下面笔者将进一步对肝脏的柔软度测量进行实验。

2.5肝脏的柔软度的测量

(a) 第1枚网格点

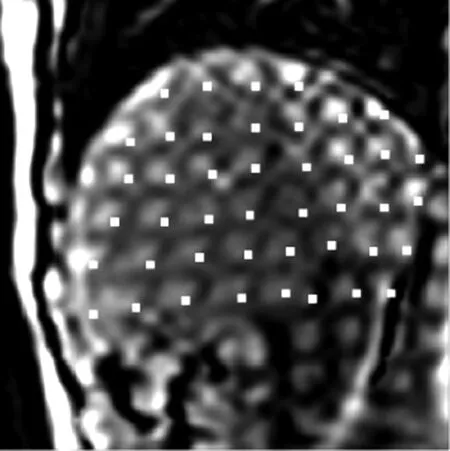
(b) 第9枚网格点

图9在MR肝脏图像上附加上的格子标签点阵列会随呼吸而移动

Fig.9Grids on MR tag images are moved by breath

①时域方面：因肝脏的柔软度在CT/MR图像上无法反映出来，故本次研究借助日本岐阜大学特有的高端核磁共振设备获取了肝脏加标签的MR图像[16](见图9)。在MR图像中附加上的格子标签点阵列会随呼吸而移动，运用本文开发的物体软硬度识别和分析的软件与计算机视觉相结合，对图像中的标签点坐标进行提取，获得本次实验的主要原始数据。采用TPS算法离散化公式计算每个标签点的弯曲能量就能测出对应的肝脏硬度，3种肝病的弯曲能量见表2，根据表2中一组数据可画出变形量分布图(见图10)，左边蓝色的点属于正常肝，中间黄色的点属于慢性肝炎和右边红色的点属于肝硬变。由图(10)可以知道肝硬变、慢性肝炎和正常肝的数据主要分布呈分阶梯上升趋势。由此可推断：肝脏越柔软，其变形量越大。即肝脏病变程度越高，其变形量越小。

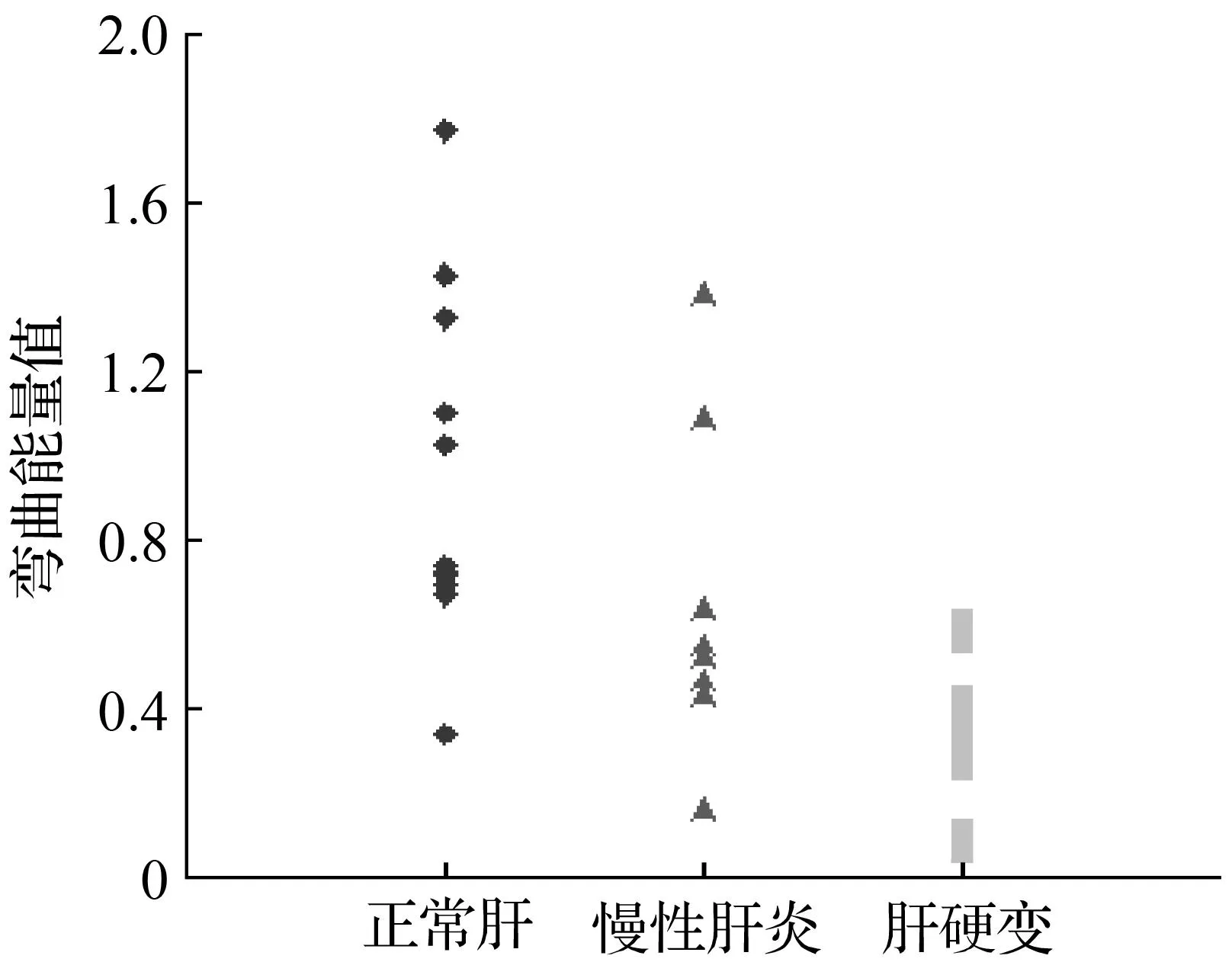
图10　变形量分布Fig.10　The distribution of deformation

表2　3种肝病的弯曲能量

②频域方面：肝脏的MR图像FFT处理如图11(a)和图11(b)，同样背景的影响比较大，需要抽取肝脏部分出来做FFT处理，频谱图呈现明显的特征变化。

(a) 第1枚MR图像及频谱图(b) 第9枚MR图像及频谱图

图11频域实验图像数据

Fig.11Experimental images in frequency domain

频域方面实验结果功率谱值数据分布如图12,正常肝脏的功率谱值普遍比异常肝脏功率谱值大，异常肝、正常肝的数据主要分布呈分阶梯上升趋势。由此笔者可以推断：肝脏越柔软，其FFT功率谱值越大。即肝脏病变程度越高，其频谱扩散的效果越明显。量化后的功率谱及弯曲能量的参数将在以后的实验中与肝硬变的等级进行比对，以期准确得出纤维化的级度。

图12　频域实验结果分布图

3结语

本文主要阐述了一种基于图像处理的物体软硬度识别和分析的方法。实验采用薄板样条(thin plate spline)算法和傅里叶变换(FFT)算法分别从空间领域和频谱领域对格子状图像特征进行解析。空域实验采用手动获取实验原数据，频域实验采用自动获取实验原数据。虽然手动获取的原数据正确性较高，但操作性比较繁琐。自动获取原数据存在不正确性数据的影响，比如：光照条件的改变的影响，但操作较简单。综合起来看，两种不同的方式获得的结果和理论最终是一致的都符合理论预测。形变的大小和TPS最小弯曲能量值、频谱值存在一定的线性关系，物体软硬度完全可以用这两种值来衡量。形变的大小是根据重量变化来得到的，同样也可以用这种方法来测量物体的重量。实验中所测未知物体的重量误差在5%以内，结果表明该方法有较高的精确度。随着进一步更多的实验调整和验证，该研究还进一步的发展空间。该测量方法对一组医学肝脏图像进行了分析，通过计量不同患者肝脏的柔软度，可以帮助医生及时准确地诊断出肝纤维化程度，达到预防肝硬变及癌变的目的。

参考文献:

[1]杨蛟龙,陈磊,贾云得.一种基于立体视觉的人与机器人交互技术[C]//第七届和谐人机环境联合学术会议(HHME2011). 北京：清华大学出版社, 2011.

[2]郝伟,张芳芳.基于计算机视觉技术的针织品瑕疵检测系统设计[J]. 计算机测量与控制, 2013, 21(9):2397-2399.

[3]安爱琴,余泽通,王宏强.基于机器视觉的苹果大小自动分级方法[J]. 农机化研究, 2008(4):163-166.

[4]刘亚敏,韩森,徐鸥明,等.疲劳试验中沥青混合料的弯拉劲度模量[J]. 广西大学学报(自然科学版),2010,35(1):127-130.

[5]李鹏博,潘荣凯,马丽,等.Mg2Sn的弹性性能和电子结构的第一性原理计算[J]. 广西大学学报(自然科学版), 2014,39(3):479-483.

[6]YEH W, HUANG S, LI P.Liver fibrosis grade classification with B-mode ultrasound[J]. Ultrasound Medicine Biology, 2003, 29(9): 1229-1235.

[7]HORNG M H.An ultrasonic image evaluation system for assessing the severity of chronic liver disease[J]. Computerized Medical Imaging and Graphics, 2007, 31(7):485-491.

[8]李俏颖,段云友.人工神经网络在超声无创定量诊断肝纤维化中的初步应用[D]. 西安:第四军医大学, 2008.

[9]闫国珍,段云友,阮骊韬,等.肝纤维化患者无创定量超声评分与临床评分之间关系的临床研究[J]. 中华超声影像学杂志, 2006, 15(8):588-590.

[10]陈永鹏,李小玲,戴林,等.超声波评分系统与病理学检查诊断代偿性乙型肝炎肝硬化的比较[J]. 中华肝脏病杂志, 2006, 14(12):936-938.

[11]FRANKE R.Smooth interpolation of scattered data by local thin plate splines.computer and mathematics with appllications[J]. Computers & Mathematics with Applications, 1982, 8(4):273-281.

[12]BOOKSTEIN L.Principal warps: Thin-plate splines and the decomposition of deformations[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1989, 11(6):567-585.

[13]高西全,丁玉美,阔永红.数字信号处理:原理、实现及应用[M]. 北京:电子工业出版社, 2010:62-83.

[14]马柏林,李丹横,晏华辉.复变函数与积分变换(修订版)[M]. 上海:复旦大学出版社, 2007:140-153.

[15]SETHI I K, JAIN R.Finding trajectories of feature point in a monocular image sequence[J]. IEEE Trans PAM I, 1987,9(1): 56-72.

[16]内山良一,張学軍,藤田広志,等. 脳と肝臓のMR画像のためのコンピュータ支援診断[J]. 画像ラボ,2012,23(2):41-46.

(责任编辑梁碧芬)

Measurement of mass and softness of an object based on image processing

ZHANG Xue-jun1,2,3, QU Xiang-he1, LEI Jin-tian1, BI Hong-mei1, LIU Tian-peng1

(1.School of Computer and Electronic information, Guangxi University, Nanning 530004, China;2.Guangxi Key Laboratory of Multimedia Communications and Network Technology (Cultivating Base), Guangxi University, Nanning 530004, China;3.Guangxi Colleges and Universities Key Laboratory of Multimedia Communications and Information Processing, Guangxi University, Nanning 530004, China)

Abstract:In general, the mass and hardness of an object are measured by using physical method, which either is complex in operation or requires specific tools. Furthermore, it is not possible to directly measure the properties inside an object. With the rapid development of robots and computer vision technology, image processing method makes it possible to identify and analyze the physical properties of an object. In this paper, we propose a novel method based on image processing to measure the hardness and softness of an object by analysis of the deformation degree in grid pattern: in the spatial field, the thin plate spline (TPS) algorithm is adopted to calculate the minimum deformation bending energy, leading to a quantitative analysis method for object's softness; in the field of spectrum, the Fourier transform (FFT) algorithm is used to calculate the difference of spectrum within a deformation frequency area before and after the change of grids, from which the relationship between softness and spectrum is investigated. Finally the experimental results are integrated in the field of space and spectrum to determine the measurement parameters of the hardness to the image. The results show that the more force on an object, the greater value of bending energy, and the greater spectrum spreading effect. Different soft materials are applied in our experiment for comparing and analyzing the experimental effect, we found that tensile has the best outcome to express the stiffness in image findings. By pressing different forces on this material, its deformation effect is remarkable, and the result is in a linear distribution as meeting the theoretical expectations. Our method of hardness measurement is applied to a set of medical images on liver with grid tags. The result indicates the ability of method on measuring the liver softness in different patients. It is expected that our method could help the doctor to diagnose the degree of liver fibrosis rapidly and accurately, and reach the goal of prevention of liver cirrhosis and cancer in future.

Key words:thin plate spline (TPS); Fourier transform; hardness; spectrum; bending energy; image processing

中图分类号：TN98

文献标识码：A

文章编号：1001-7445(2016)02-0541-13

doi:10.13624/j.cnki.issn.1001-7445.2016.0541

通讯作者：张学军(1969—)，男，广西邕宁人，广西大学教授，博士； E-mail: xjzhang@gxu.edu.cn。

基金项目：国家自然基金资助资助项目(81460274，61262027)；广西大学大学生实验技能和科技创新能力训练基金资助项目(SYJN20130728 )

收稿日期：2015-12-01；

修订日期：2016-01-25

引文格式：张学军，瞿祥和，雷锦添，等.基于图像处理的物体质量与软硬度的测量[J].广西大学学报(自然科学版)，2016，41(2)：541-553.