企业战略联盟中多人多产品合作生产的成本分摊研究

徐鲲鲍新中(北京联合大学，北京　100101)

企业战略联盟中多人多产品合作生产的成本分摊研究

徐鲲鲍新中
(北京联合大学，北京100101)

〔摘要〕合作博弈理论在企业联盟收益分配和成本分摊中得到了广泛应用，但一般都是单产品问题，而多产品合作生产的成本分摊问题相关研究却很少。本文从合作博弈的视角研究了企业战略联盟中各参与企业合作生产多种产品时的成本分摊问题，构建了一个多人多产品合作博弈模型，给出了博弈应满足的公理化性质，并基于夏普利法给出了该博弈的解函数表达式，同时还给出了单位产品成本函数的表达式。使用该博弈模型首先可以实现战略联盟的总成本在各参与企业间的分摊，还可以将总生产成本在该联盟生产的各产品之间进行分摊。最后用算例证明了该方法的可行性及合理性。

〔关键词〕企业战略联盟合作博弈成本分摊夏普利值收益分配

引言

自企业战略联盟在20世纪90年代兴起以来，其作为一种新型的管理实践一直备受关注。企业界和理论界从经济学、管理学、社会学等多个角度对企业战略联盟的组织性质、形成动因、联盟的组建、联盟的管理［1－3］以及联盟的利益分配(成本分摊)、联盟的稳定性等［4－10］内容展开了研究。联盟合作收益分配或成本分摊的合理性是联盟能够保持持续稳定的基础，国内外学者对此展开了多方面的研究。

合作博弈理论不讨论理性的个人如何达成合作的过程，而是直接讨论合作的结果与收益的分配。合作博弈的主要问题就在于如何在参与人中间分配由于合作而带来的额外的收益及分配联盟的总成本。以合作博弈为基础的成本分配理论已经被众多学者应用到许多实践领域当中，运用较多的是对于一些大型公共基础设施的成本分配问题［11］、电力通讯网络领域的成本分摊问题［12］等。也有学者将合作博弈理论运用到企业合作联盟的成本和利益分配中［13－15］。

战略联盟有多种形式，按照其合作领域，一般可以分为技术合作联盟、研发联盟、市场联盟和生产联盟等形式，本文研究的是生产合作战略联盟之间的成本分配问题。目前，在利用合作博弈理论来进行生产合作战略联盟收益(成本)分配的研究中，一般都只涉及生产一种产品的成本或收益分配(也可以理解为将生产成本函数视同为线性函数，认为生产成本函数与产量之间是线性关系)。但是，当合作联盟生产的产品种类大于或等于2，且各产品之间的成本不独立、生产成本函数为非线性函数时，不仅要将联盟总生产成本在联盟各参与企业之间进行分配，还要将联盟总生产成本在各产品之间进行分配。而在现实生活中，产品联盟合作生产多产品的情况很常见，比如石油产业、化工产业等，一个生产链所产出的产品很多，而且各产品之间的成本并不独立。这时，若仍使用传统的成本分摊方法计算各种产品的单位成本，所得结果的准确性就难以保证，甚至使用传统的分摊方法根本无法进行分摊。本文基于合作博弈思想用一个博弈族描述了企业战略联盟中多产品合作生产的成本分摊问题，构建了多人多产品合作博弈成本分摊模型，给出了博弈应满足的公理化性质，并基于夏普利值法给出了该博弈的解函数表达式，同时还给出了单位产品成本函数的表达式。

1　多人多产品合作条件下合作博弈相关概念的重新界定

对相同的产品集合感兴趣的企业可以通过组成产品联盟的形式或签订合作协议的形式合作生产以获得所需数量的产品。无论企业间采用何种方式构建企业战略联盟，都要进行收益(成本)分摊，而一个公平、合理、能为联盟中所有企业都接受的成本(收益)分摊方案，对于维持联盟的稳定性、保证后续合作而言具有重要意义。

一般的合作博弈分配模型只涉及一种产品的分配(或者说将生产成本函数视同为线性函数，认为生产成本函数与产量之间是线性关系)，而本文所要解决的是多种产品的生产成本分摊问题，生产函数为非线性函数，因而在模型的表达上有较大区别。基于合作博弈理论的相关原理以及关于多产品合作生产的相关研究［16］，这里将重新界定合作博弈中函数、集合等要素的表达方式。

令N = { 1，2，…，n}表示大战略联盟，其中n为正整数，表示参与企业的个数。令P表示集合N所有非空子集的集合。令S表示参与企业之间任意组成的战略联盟，S⊂P;假定大联盟N中的每一个参与企业都对相同的产品集M = { 1，2，…，m}感兴趣，该产品集内的所有产品都可以通过执行生产项目获得。值得说明的是，大联盟N中的每一个参与企业都可以独立进行生产而获得所需要的产品量，也可以通过组成战略联盟合作生产以满足所需产量。

对于每一个联盟S⊂P而言，给定产品向量x ∈Rm，都有一个既定的生产成本函数fs∶Rm→R。我们定义产品向量x = (x1，x2，…，xm)∈Rm+，也就是说，参与人都只对正的产量感兴趣。此外，生产成本函数fs是非线性函数，它仅取决于产品总量而不取决于产品在参与企业之间的分配方式。函数fs具有连续的一阶偏导数，且f(0) = 0，也就是说在产量为零时，成本也为零。

定义y = (y1，y2，…，yn)∈Rn×m+= RNM，其中RNM是大联盟N的产品空间，向量y = (y1，y2，…，yn)表示参与企业所需求的产量。yi= (yi1，yi2，…，yim)∈Rm+，其中，yij表示第i家企业对第j种产品的需求量。

定义1:给定成本函数f和产品向量x，定义函数c(f，x)为产品的单位成本函数:

c(f，x) = (c1(f，x)，…，cj(f，x)，…，cm(f，x) )∈Rm

其中，cj(f，x)是第j种产品的单位成本。对于任意联盟S而言，单位成本函数c(fS，x)将生产成本fS在该联盟所生产的各单位产品之间进行分配。

定义2:给定一个有限的参与企业集合N，多人多产品合作博弈的特征型是有序数对(N，vy)，其中，函数vy被称为该合作博弈的特征函数，是从集合S到实数集的映射。对于任意给定的参与企业联盟而言，vy表示该联盟的得益(payoff)，这项得益是由于参与企业之间组成联盟合作生产而给联盟带来的收益，其本质是一种成本节约。特征函数的一般表达式为:

式(1)中，表示第i个参与企业单独生产所需产量时的成本，而表示参与企业所组成的战略联盟S合作生产产品所产生的总成本。由此我们可以得知，vy(S)表示:相对于单独执行项目而言，联盟S中的参与企业因合作而获得的成本节约，即联盟的得益。

此外，对于任意i∈N，特征函数vy都满足: vy({ i} ) =0，也就是说，博弈(N，vy)是0——标准化的。

如果多人多产品合作博弈满足超可加性条件，即:对于任意S，T∈P，且S∩T =?而言，都有vy(S∪T)≥vy(S) + vy(T)，那么我们认为该模型是适当的、可行的。

定义3:定义合作博弈(N，vy)的分配集I(N，vy)为:，且对于∀i∈N，都有zi≥vy({ i } } )

从定义中可以看出，I(N，vy)是所有符合个体理性和集体理性的分配方案z的集合。集合中的每个分配方案都能将大联盟N的得益vy(N)在所有参与企业之间进行完全分配。

定义4:函数F∶Ω→Rm是一个解，如果它给每个合作博弈(N，vy)分配以分配集I(N，vy)中的一个子集。Fi(N，vy)表示大联盟N的总得益中分配给第i家参与企业的份额。

定义5:对于任意给定的产品向量y = (y1，y2，…，yn)∈RNM，定义投资函数G为从Ω到Rm的映射，第i个参与企业的投资额可以表示为:

第i个参与企业的投资额在数值上等价于他独立完成生产的生产成本与他从大联盟N中分得的得益之间的差值。其本质是第i个企业参与战略联盟N，为获得其所需数量的产品最终所付出的总成本。

2　多人多产品合作博弈的公理化性质

2. 1单位成本函数的公理化性质

基于合作博弈理论的相关原理以及关于多产品合作生产的相关研究［16］，这里描述并讨论多人多产品合作博弈中单位成本函数c(f，x)应当满足的4个公理化性质(或必要性条件)，同时满足这4个公理化性质的单位成本函数是唯一的，本文给出了该单位成本函数的一般表达式。单位成本函数c(f，x)应当满足的4个公理化性质(公理1～4) :

公理1:可收回性公理，如果对于任意联盟S ⊂P而言，都有:

则称单位成本函数具有可收回性。上式表明:联盟的生产成本能够在所输出的各单位产品之间进行完全分配。也就是说，如果联盟S中的参与人决定要实施该开发项目，按照单位成本函数给各单位产品的成本之和应当包含且不超过生产成本fS(x)。

公理2:可加性公理。如果对于任意联盟S⊂P而言，给定函数fS、gS和hS，且hS= fS+ gS，都有:

c(fS，x) + c(gS，x) = c(hS，x)

则称单位成本函数是可加的。上式中，函数fS和函数gS表示总成本hS的两个不同的组成部分。上式表明了c(f，x)的可加性，即:如果生产成本可以分解成不同的组成部分，那么任意产品最终的单位成本都应当是其部分成本的单位成本之和。

公理3:单调性公理。如果对于任意联盟S⊂P而言，生产成本函数fS在区间{ z∈Rm∶0≤z≤x}上是非递减的，即: x≥z⇒fS(x)≥fS(z)，都有: c(f，x)≥0。则称单位成本函数具有单调性。这意味着，如果生产函数是非递减的，那么产品的单位成本cj(f，x)是非负的。在这里，“函数fS是非递减的”表示:对于每一种产品而言，如果生产数量增加，生产成本也会随之增加，也就是说更低的生产成本不会生产出更多的产品。

同时满足前3个公理化性质的单位成本函数有很多，即如果仅提出前3个条件，可能出现多种不同的分配方案。因而，第4个公理化性质(聚集不变性)要求在特定的情况下使用特殊的方法将成本分配给单位产品，其特殊性是决定单位成本函数的唯一性的一个重要因素。

公理4:聚集不变性公理。如果对于任意联盟S⊂P而言，给定产品向量d = (d1，…，dm)∈Rm(d＞0)，若:

都有:

则称单位成本函数是一个聚集不变量。上式表明单位成本函数的表达式形式不受函数fS(x)和变量x的表达形式变化影响。如果两种产品在本质上属于同一种产品，但由于所使用的计量单位不同(比如同一种石油的产量可以用美制加仑或英制加仑计量)，而采用不同的产品向量表示，根据本公理化性质便可判断出这两种产品究竟是不是同一种物质。

同时满足上述4个公理化性质的单位成本函数的表达式是唯一的:

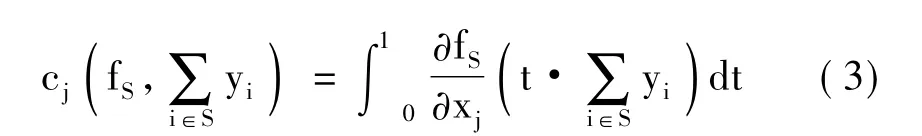
根据Billera和Heath两人所提出的成本分配程序［18］，以及单位成本函数所满足的公理1～4中的条件，我们可以证得本文所提出的单位成本函数的表达形式是唯一的，并且以式(3)的形式存在。

对于任意联盟S而言，根据式(3)，我们可以计算该联盟产出中各产品的单位成本。

2. 2解函数的公理化性质

根据合作博弈解函数的性质特点，这里来讨论多人多产品合作博弈的解函数Fi(N，vy)所应满足的几个公理化性质(公理5～8) :

公理5:虚拟性公理。博弈(N，vy)的参与人被称为虚拟参与人，如果对于任意联盟S⊂N{ i}而言，都有vy(S∪{ i} ) = vy(S)。也就是说，如果一个参与人是虚拟参与人，那么他加入还是不加入联盟对联盟的得益没有影响。

解函数Fi(N，vy)满足虚拟参与人性质，简称虚拟性，对于博弈(N，vy)中的虚拟参与人，Fi(N，vy) = 0。也就是说，对于没有做出贡献的参与人——虚拟参与人，不分配给他任何得益。实际上，虚拟性公理是边际原则的一种弱形式。

公理6:解函数Fi(N，vy)具有匿名性，如果对于任意博弈(N，vy)，任意i∈N以及任意排列π，都有:

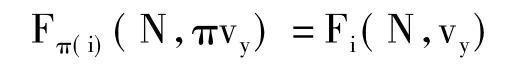
其中，博弈πvy定义为:对于任意联盟S⊂P而言，πvy(π(S) )≡vy(S)。也就是说，联盟中处于同样地位的参与人所分配到的得益是相同的，应该平等地对待地位相同的人。分配给某个参与人的得益应该按照其对联盟的贡献大小，而不管他是谁。

如果对于任意联盟S⊂P而言，给定函数fS、gS和hS，且hS= fS+ gS，假定与这些成本函数相对应的博弈分别为(N，vy)、(N，v'y)、(N，v″y)，那么，根据前文中对可加性公理的表述，有:

公理7:聚合性公理。如果对于任意博弈(N，v'y)、(N，v″y)，有:

则称解函数Fi(N，vy)具有聚合性，该公理要求任何两个相互独立的博弈的联合所组成的新博弈的解是原来两个博弈的解之和。

公理8:规模效应公理。如果对于联盟S，T⊂P，且S∩T =?，都有:

则称解函数Fi(N，vy)具有规模效应，由若干个相互独立的较小联盟合并而成的大联盟的总成本小于或者等于原各联盟的成本之和，也就是说，参与人对某个联盟的边际贡献随着联盟的规模扩大而增加。

引理1:如果多人多产品合作博弈(N，vy)同时满足公理1和公理8，那我们说该博弈是适当的、可行的，也就是说，该博弈满足超可加性。

合作博弈(N，vy)是超可加的，如果对于任意联盟S，T⊂P，且S∩T =?，都有:

vy(S) + vy(T)≤vy(S∪T)

该式表明，当任意两个联盟的交集为空集的时候，这两个联盟中的所有参与人组成的新联盟的总利润总是不小于原先的两个联盟的利润之和。这种博弈称为超可加博弈。

对引理1中结论的证明:

对于任意联盟S，T⊂P，且S∩T =?，都有:

即多人多产品合作博弈(N，vy)满足超可加性。

3　多人多产品合作博弈成本分摊模型及其求解

3. 1建立多人多产品合作博弈成本分摊模型

合作博弈成本分摊模型的建立是以3个条件为前提的，即:有效性、个体理性和集体理性［16］。多人多产品合作博弈成本分摊模型的建立也要满足这几个条件。

条件1:个体理性。每个参与人从联盟总成本中分摊到的金额，要小于其独立完成自身项目所要花费的成本，否则，从自身利益出发，该企业将不会接受成本分摊方案。即:

其中，C(i)为第i个参与人不与任何人结盟时所发生的成本数额。

条件2:有效性。联盟成本应在成员企业之间完全分摊，即:

其中，C(N)表示n个参与人的总需分摊成本，实际上也就是所有参与人全部参加合作时所需要分摊的总成本发生额。

条件3:集体理性。在多人合作博弈中还需要满足联盟和理性条件，即:

同时满足有效性、个体理性和集体理性的成本分摊方案为内部稳定合作分摊，Fi(N，vy)为稳定解，否则称为不稳定的合作。这里得到内部稳定的多人多产品合作博弈成本分摊模型。

3. 2基于夏普利值的多人多产品合作博弈模型的解

在多人多产品合作博弈(N，vy)中，由于公理1可收回性公理、公理2可加性公理和公理8规模效应公理都得到了满足，说明该博弈是适当的、可行的，也就是说，该博弈满足超可加性条件。而且该合作博弈满足虚拟性、匿名性、可加性等公理化性质，则根据Shapley在1953年的文章中给出的夏普利值表达式，将特征函数的形式替换为定义3中的形式，就得到了解函数的一般表达式。

在多人多产品合作博弈(N，vy)中，对于任一给定产品向量y = (y1，y2，…，yn)∈RNM而言，都有唯一的解F满足公理1～8，其表达式为:

其中，对于∀i∈N及∀S⊂P而言，特征函数vy的表达式为:

成本分摊函数cj(fS，x)的表达式为:

4　　算例分析

4. 1算例假设

假定目前化工市场上有甲、乙、丙、丁4家企业，他们希望通过合作研发生产A、B两种产品，共同占领同类产品市场。A、B两种产品在同一生产流程中生产，共同消耗机器设备、人员工时以及生产车间发生的其他各种费用，两种产品的成本间存在相关性，很难单独进行核算。尽管这四家企业完全具备独立研发生产产品A和B的实力，但为了降低成本，利用规模效应带来的成本降低，4家企业开始寻求合作，建立了一个企业战略联盟，合作生产所需的两种化工产品。

在本算例中，我们假定:参与人集合为N = { 1，2，3，4}，依次代表4家化工甲、乙、丙、丁;产品集合为M = { 1，2}，分别代表产品A和B;参与人联盟的集合为P = { { 1}，{ 2}，{ 3}，{ 4}，{ 1，2}，{ 1，3}，{ 1，4}，{ 2，3}，{ 2，4}，{ 3，4}，{ 1，2，3}，{ 1，2，4}，{ 2，3，4}，{ 1，2，3，4} }。

对于任意联盟S⊂P而言，生产成本函数fS(x1，x2)都是给定的，其中x1和x2分别表示联盟S所需要的产品A和产品B的数量。在本算例中，假定生产成本函数的表达式为道格拉斯生产函数的形式，即: f(x1，x2) = axα1xβ2，其中α，β＞0且α +β＜1。当然，在现实中，生产成本函数要更加复杂，而且不同联盟的生产函数一般不同，但为了简化计算，本例中假定所有联盟的生产成本函数相同，为f(x1，x2) = 2x0. 41x0. 52，即a = 2，α= 0. 4，β=0. 5。各企业所要求的两种产品的数量如表1所示:

表1　企业所需产量表

4. 2成本分摊模型的应用及计算

成本分摊程序:根据算例说明中给出的数据，以及本文给出的函数表达式以及多人多产品合作博弈解的表达式，我们将分别计算出各联盟的生产成本、产品的单位成本、特征函数vy的值，然后根据Shapley Value法计算出合作博弈的解，并且根据投资函数Gi(N，vy)的表达式求出各企业应当分摊的成本额。

表2　各成本及特征函数值结果表

表2中，第一行列示了各联盟所要求产品A的产量x1，第二行列示了各联盟所要求产品B的产量x2。第三行列示了根据生产成本函数表达式和一、二行数据计算的各联盟的生产成本fS。第四行列示了根据单位成本函数计算得到的产品A的单位成本c1，第五行列示了产品B的单位成本c2。最后一行列示了根据特征函数vy的表达式所计算出的各联盟的特征函数值。

下面以联盟{ 1，2，3}为例列出各成本、函数值的计算过程:

①计算联盟要求的产量x1和x2: x1=6 +3 + 4 =13; x2=4 +5 +3 =12。

②计算联盟的生产成本fS: fS= 2×130. 4× 120. 5=19. 33，即:联盟{ 1，2，3}的总生产成本为19. 33。

③计算产品A的单位成本c1:

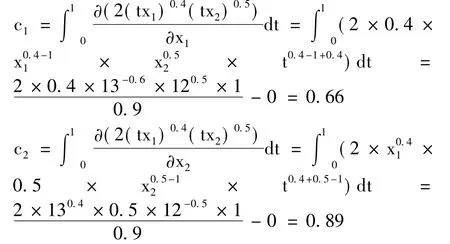
即:在联盟{ 1，2，3}中，产品A的单位成本为0. 66，产品B的生产成本为0. 89。

④计算联盟{ 1，2，3}的特征函数值:

vy({ 1，2，3} ) =0. 61×6 +1. 14×4 +1. 03×3 +0. 77×5 + 0. 67×4 + 1. 12×3－(0. 66×13 + 0. 89×12) =1. 83

即:企业甲、乙、丙三者通过构建联盟{ 1，2，3}而获得了1. 83的得益，该得益的本质是一种成本节约。该节约额应在大联盟的参与企业之间进行分配。这里运用Shapley Value法计算甲企业应分得的联盟得益为例介绍合作博弈解的计算过程:

根据Shapley Value法计算博弈解时，按照下式求解:

在集合P中，一共有8个联盟中包含甲企业，各联盟的联盟人数、特征函数、形成该联盟的概率以及解函数的计算过程如表3所示:

表3　企业甲的Shapley Value计算过程表

根据表3中的数据，可计算出甲企业所分得的得益为:

F1(N，vy) =0. 06 +0. 08 +0. 06 +0. 10 +0. 11，+0. 10 + 0. 38 = 0. 89，即甲企业因参与各联盟所分得的联盟得益的期望值。同理，可以计算出其他3家企业所分得的得益分别为F2(N，vy) = 0. 53，F3(N，vy) =0. 79，F4(N，vy) =0. 56。

表3中，，yi)×yij］－Fi(N，vy)可以算得各企业最终所分摊的生产成本分别为:

G1(N，vy) =8. 19－0. 89 =7. 30;

G2(N，vy) =6. 94－0. 53 =6. 41;

G3(N，vy) =6. 03－0. 79 =5. 24;

G4(N，vy) =5. 38－0. 56 =4. 82。

至此，已经得到了甲乙丙丁各企业为获得所需产品量而最终分摊的成本，并且得到了产品A 和B各自的单位成本，即完成了本算例中多人合作生产多产品的成本分摊问题。

5　结论

合作博弈理论在企业联盟单产品合作生产的收益分配和成本分摊中已经得到了广泛的应用，而本文则研究了企业联盟中参与企业合作生产多种产品时的成本分摊问题，得到以下结论:

(1)多产品合作生产的成本函数一般为非线性函数，成本函数和各产品的产量之间并不是简单的线性关系，而是具有规模效应的。使用传统的分配方法难以将联盟的生产成本在各产品之间准确分配，因而本文在给出了产品单位成本函数应满足的公理化性质(公理1～4)之后，得到了单位成本函数的表达式，该式是唯一能够同时满足公理1～4的表达形式。

(2)本文用一个博弈族描述了企业战略联盟中多产品合作生产的成本分摊问题，构建了多人多产品合作博弈模型，给出了博弈应满足的公理化性质(公理5～8)，并应用Shapley Value法得到了该博弈的解，该博弈解是唯一能够同时满足公理5～8的成本分配方案。

最后通过算例应用，验证了多人多产品合作博弈及其解的有用性，即能够成功地将生产成本在联盟中各企业和各产品之间进行分配。

参考文献

［1］Ilaria G．，Pierpaolo P．Supply Chain Coordination by Revenue Sharing Contracts［J］．Intemational Journal of Production Economics，2004，89: 131～139

［2］王路，吴松强，等．小微企业横向战略联盟形成机理研究［J］科技管理研究，2015，(4) : 204～208

［3］赵炎，周娟．企业合作网络中嵌入性及联盟类型对创新绩效影响的实证研究［J］．研究与发展管理，2013，25 (1) : 12～23

［4］Carsten H．，Peter S．How Should the Cost of Joint Risk Capital be Allocated for Performance Measurement?［J］．European Journal of Operational Research，2008，187: 208～227

［5］孙耀吾，卫英平．基于复杂网络的高技术企业联盟知识扩散AIDA模型与实证研究［J］．中国软科学，2011，(6) : 130 ～139

［6］周杰．联盟能力、关系质量与战略联盟企业间知识转移关系研究［J］．情报科学，2014，32 (12) : 123～128

［7］杨益民．企业联盟决策机构的席位分配及成员的势力分布和位次竞争策略［J］．系统工程理论与实践．2011，31 (7) : 1264～1271

［8］赵炎，王冰．战略联盟网络的结构属性、资源属性与企业知识创造［J］．软科学，2014，28 (7) : 59～64

［9］詹也，吴晓波．企业联盟组合配置战略与组织创新的关系研究——基于我国汽车行业的多案例研究［J］．科学学研究，2012，30 (3) : 466～473

［10］刘辉，等．我国联盟标准化治理模式的理论与实证研究——基于政府的视角［J］．工业技术经济，2013，(9) : 17 ～25

［11］Fragnelli V．，Iandolino A．A Cost Allocation Problem in Urban Solid Wastes Collection and Disposal［J］．Mathematical Methods of Operation Research，2004 (59) : 447～463

［12］Choudhury N. B．，Goswami，S. K．．Artificial Intelligence Solution to Transmission Loss Allocation Problem［J］．Expert Systems with Applications．2011，38: 3757～3764

［13］Zheng Y．，Zhang，S．，Chen X．Application of Modified Shapley Value in Gains Allocation of Closed－loop Supply Chain under Third－Party Reclaim［J］．Energy Procedia．2011，(5) : 980～984

［14］鲍新中，刘澄，张建斌．基于EOQ的集成供应成本分摊问题研究［J］．中国管理科学，2009，17 (1) : 101～106

［15］Moshe D．，Bruce C. H．，Wei，C．The Cost Allocation Issue in Joint Replenishment［J］．Int．J. Production Economics，2012，135: 242～254

［16］Lech K．，Piotr B．Cooperative Game Solution Concepts to a Cost Allocation Problem［J］．European Journal of Operational Research，2000，122: 258～271

［17］Billera，L. J．，Heath，D. C．．Allocation of Shared Costs: A Set of Axioms Yielding a Unique Procedure［J］．Mathematics of Operations Research 1982，7 (1) : 32～39

［18］Shapley，L. S．．A Value for N－person Game［J］．Annals of Mathematics Studies，1953，28

(责任编辑:王平)

Research on Cost Allocation of Multiple Goods Cooperative Production in Enterprise Strategic Alliance

Xu Kun Bao Xinzhong
(Beijing Union University，Beijing 100101，China)

〔Abstract〕Cooperative game theory has been widely used in profit and cost allocation of enterprice alliance under singleproduct cooperation，but not multi－products cooperation．This paper mainly dealt with the cost allocation of multi－products cooperative production in enterprise strategic alliance．A cooperative game model is put forward for cost allocation problem which describing cooperation of players interested in multiple goods obtained from a joint project．Under a set of axioms imposed on the game and axioms describing reasonable requirement of per－unit cost function，the solution based on the Shapley Value is proposed and discussed．By using this model，the total cost of the alliance could be allocated within the players，and also could be allocated within the products in the same time．Finally，a case is used to prove the rationality and the feasibility of this model．

〔Key words〕enterprice strategic alliance; game theory; cost allocation; shapley value; income distribution

作者简介:徐鲲，北京联合大学管理学院教授。研究方向:供应链金融。鲍新中，北京联合大学管理学院教授，博士，创新企业财务管理研究中心主任。研究方向:科技企业投融资管理。

基金项目:国家社会科学基金项目“基于第三方风险动态监控平台的知识产权质押融资模式研究”(项目编号: 14BGL034) ;北京社科基金项目“电商双边市场供应链融资与北京小微企业融资体系优化研究”(项目编号: 14JGC097)。

收稿日期:2015—12—01

〔中图分类号〕F224. 32; F275. 3

〔文献标识码〕A

DOI:10．3969/j．issn．1004－910X．2016．04．008