考虑公平性的两阶段系统固定成本分摊DEA模型

昂 胜, 范婷婷, 杨 锋

(中国科学技术大学 管理学院,安徽 合肥 230026)

0 引言

固定成本分摊问题具有很高的现实意义，例如跨国公司需要将信息平台建设维护费用和广告公关费用等成本在子公司间分摊[1]，商业银行总行将建设成本和系统维护成本在二级分行间分摊[2]。而DEA方法是一种非参数线性规划方法，其权重选择具有一定灵活性[3]，且可用于研究可行分摊方案对效率评估的影响[4]，因此利用DEA方法处理固定成本分摊问题成为近年来的研究热点之一。

固定成本分摊问题不仅存在于多个决策单元之间，也存在于具有多阶段生产过程的决策单元内部，例如，商业银行中各分行的金融部门和投资部门共同在分摊公共信用信息共享的系统成本[5]。在已有关于两阶段系统固定成本分摊的研究中(如，[5～9])，较少有方法考虑分摊方案的公平性问题。例如，Li等[5]为使决策单元整体和各阶段在分摊后均为有效，可能会使得某些决策单元分摊较多的固定成本。Yu等[6]为保证效率不变，可能同样存在极端分摊的情况。而在实际情况下，这种极端分摊方案并不公平，往往无法被企业所接受。因此，如何公平地将固定成本分摊给具有两阶段生产过程的决策单元及其各阶段是一个具有实际意义的问题。Li等[4]在单阶段系统固定成本分摊研究中首次引入非自利原则，认为决策单元在各自所提出的固定成本分摊方案中，其自身分摊的固定成本数量不应小于其他决策单元的分摊数量，即提出分摊方案的决策单元分摊该方案中最大的固定成本数量。由于这种对自身的分摊行为满足非自利原则，因此各决策单元分摊给自身的固定成本可被所有决策单元接受。该原则适用于缺乏集中决策者情形下的资源分配和固定成本分摊等决策问题，可在实际经济环境中为决策者提供决策支持。本文将非自利原则引入到两阶段系统的固定成本分摊问题中，针对群组式组织结构提出新的两阶段系统固定成本分摊模型。

本文的主要创新工作是在两阶段系统固定成本分摊问题中，考虑公平性因素对分摊方案的影响，通过非自利原则求出整体和阶段的固定成本分摊上界，并对分散决策环境下的群组式组织结构，构建新的两阶段系统固定成本分摊模型，使得分摊结果更为公平。最后本文通过实际算例验证了新模型的可行性和适用性。

1 方法与模型

1.1 两阶段系统固定成本分摊模型

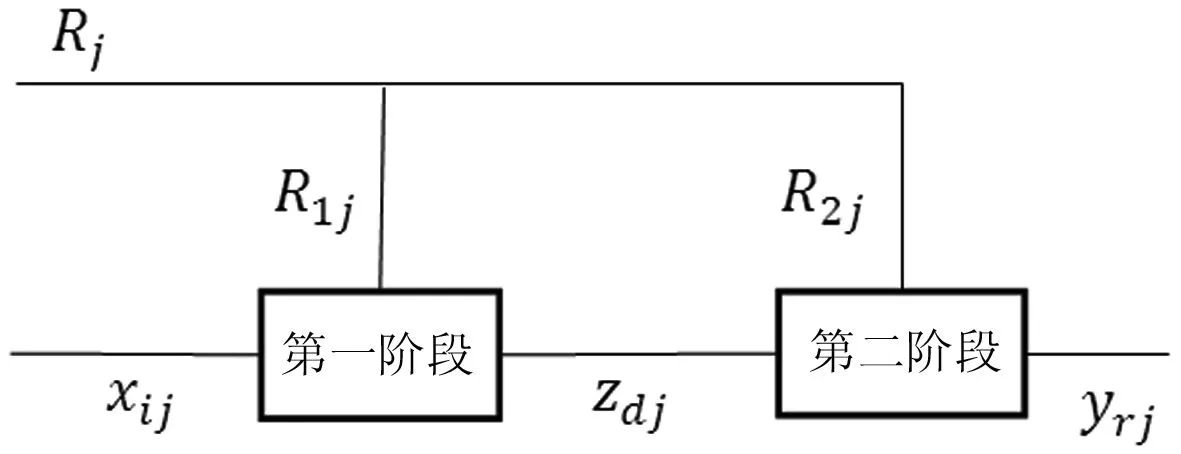
图1 考虑固定成本分摊的两阶段系统

根据Chen等[11]对两阶段系统效率的定义，第一阶段和第二阶段效率分别为

决策单元的整体效率可表示为两个阶段效率的加权和，即

有w1+w2=1。则在规模报酬不变假设下，可构建如下的效率评价模型[9]:

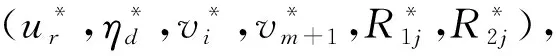
此外，各DMU分摊前的整体效率和阶段效率可通过求解令R=0时的模型(1)得到[5]。由于模型(1)仅追求DMUo效率最大化，并未考虑到对其他DMU的成本分摊是否公平，因此该方案可能不会被其他DMU所接受。换句话说，DMUo根据模型(1)所提出的分摊方案是自利的，该方案可能会损害其他DMU的利益，因此不被其他DMU认可。为了实现更公平的分摊，本文通过非自利原则提出两阶段系统固定成本的分摊方法。

1.2 群组式组织结构的固定成本分摊模型

在实际情况下，具有两阶段系统的决策单元往往具有多个群组。例如，在零件供应商和汽车制造商构成的多个两级供应商网络中，所有零件供应商和汽车制造商可分别构成供应商群组和制造商群组[12]。上述群组式组织结构可通过图1阐述，即存在若干个两阶段生产系统，且不同生产系统的同一生产阶段构成群组[12]，每个群组均可以自身整体效率最大化为目标，提出一组分摊方案。但该方案可能仅利于某个群组自身，无法被另一群组接受。在非自利原则下，规定提出分摊方案的群组要在其方案中分摊最大的固定成本，使得分摊方案并不有利于该群组，因此该群组在其方案中所分摊的固定成本可被另一群组接受。对于包含多个子阶段的群组，不仅要保证群组整体的分摊成本满足非自利原则，即提出分摊方案的群组整体所分摊的总成本不小于其他群组的总成本，也要保证群组各子阶段的分摊成本满足非自利原则，即该群组各子阶段分摊的成本不小于其他群组对应子阶段的成本。对于图2所示的组织结构，有如下定义：

图2 群组式组织结构

定义1对于任一群组Mg(g∈G={1,2})所提出的固定成本分摊方案，若Mg分摊的总成本Rg不小于群组Mg′(g′∈G={1,2},g′≠g)的总成本Rg′，且Mg各阶段分摊的成本Rgj不小于Mg′对应阶段的成本Rg′j，即：Rg≥Rg′,Rgj≥Rg′j(g′∈G={1,2},g′≠g,j=1,…,n)，则Mg提出的分摊方案满足两阶段系统的非自利原则。

定义1表明，相对于其他群组整体和内部各阶段而言，提出分摊方案的群组Mg整体及其内部各阶段均分摊该方案中最大的成本数量，即满足非自利原则，因此群组Mg分摊给自身的成本可被所有群组认可。而在非自利原则下，群组Mg分摊给自身的成本为Mg所能接受的成本上界，若分摊成本超出此上界，可能会造成Mg效率值进一步降低，对Mg而言是不公平的。

对于群组Mg的整体效率，可根据Chen等[11]对两阶段系统整体效率的定义方法，定义群组Mg的整体效率为群组内部各阶段效率的加权和，其中权重为各阶段的加权投入与所有阶段加权投入之和的比值。对于图2所示的组织结构，其群组M1内部各阶段的权重为

群组M2内部各阶段的权重为

第一阶段和第二阶段效率分别为

则群组M1的整体效率可表示为

群组M2的整体效率可表示为

σM1，σM2∈[0,1]。对于群组整体效率与群组内部各阶段效率之间的关系，有如下定理：

定理1群组整体效率为1当且仅当群组内部各阶段效率均为1。

根据以上分析，对于图2所示的组织结构，以群组M1在非自利原则下提出分摊方案，可构建如下的固定成本分摊模型：

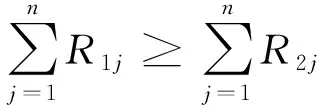
此外，对于模型(3)存在以下定理：

定理2模型(3)至少存在一组分摊方案，使得群组M1的整体效率值为1。

定理2表明，至少存在一种群组M1在非自利原则下的分摊方案，该方案可使得群组M1达到整体有效。并且根据定理1可知，群组M1内部各阶段也均为有效，即所有决策单元的第一阶段均为有效。

类似地，以群组M2在非自利原则下提出分摊方案，可构建如下的固定成本分摊模型:

令υm+1R1j=F1j，υm+1R2j=F2j，模型(4)通过Charnes-Cooper变换[13]转化为线性化模型(5):

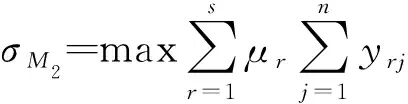
类似模型(2)，模型(4)存在以下定理：

定理3模型(4)至少存在一组分摊方案，使得群组M2的整体效率值为1。

定理3表明，至少存在一种群组M2在非自利原则下的分摊方案，该方案可使得群组M2达到整体有效。并且根据定理1可知，群组M2内部各阶段也均为有效，即所有决策单元的第二阶段均为有效。

尽管M1与M2均在非自利原则下给出了分摊方案，但两种分摊方案可能是不一致的。考虑到各群组都想分摊尽可能少的固定成本，同时尽可能提高效率，为了实现最终公平的分摊，提出如下模型:

maxβ+γ

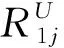
令υm+1R1j=F1j,υm+1R2j=F2j，模型(6)通过Charnes-Cooper[13]变换转化为模型(7):

maxβ+γ

值得说明的是，由于线性模型可能存在多解情况，本文求解的固定成本分摊方案存在不唯一性，可进一步借鉴Chu等[8]和Li等[5]的研究获得一组唯一解。

2 应用算例

表1 27家商业银行的投入产出数据表

表2 27家商业银行分行的成本分摊及效率结果表

3 结论

本文针对两阶段系统固定成本分摊问题中的公平性因素对分摊结果的影响，充分考虑了群组式组织结构情形下各决策单元及群组的分摊预期，基于非自利原则得到成本分摊上界，并进一步提出新的两阶段系统成本分摊模型，使得分摊方案更具公平性，进而更容易被决策单元及群组所接受。本文的方法能够更好的实现固定成本在两阶段系统之间以及内部的分摊，且充分考虑了实际环境下的应用问题，为现实中的成本分摊问题提供了新思路。此外，由于本文仅基于简单的两阶段系统结构进行探讨，未来研究中可将此方法拓展至更一般的网络结构，如多阶段串联、并联或混联结构等。