Fresnel积分的再推广

钟文体（华南师范大学数学科学学院，广州510631）



Fresnel积分的再推广

钟文体
（华南师范大学数学科学学院，广州510631）

［摘 要］使用复变函数论中的方法计算了一类复杂的反常积分，这些反常积分都是Fresnel积分的推广．

［关键词］反常积分；Fresnel积分；Cauchy定理；Γ函数

众所周知，使用复方法能计算很多复杂的实积分．在本文中，我们借助复分析提供的强大方法，同时引入Γ函数，推广了Fresnel积分，得到了一类很广泛的反常积分的计算公式．

1　第一步推广

先给出一个初等但有用的不等式并略去证明，即下面的引理．

首先有下面的结论．

定理1．1 设φ∈［0，π／4］，则

证 考虑复变函数

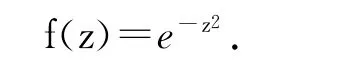
取如图1所示的积分路径γ．把γ分为若干部分，其中γR是中心在原点，圆心角为φ，半径为R的圆弧．因f（z）在γ所围成的区域内解析，根据复变函数论中的Cauchy定理，有

而

上面的估计使用了引理1．

图1

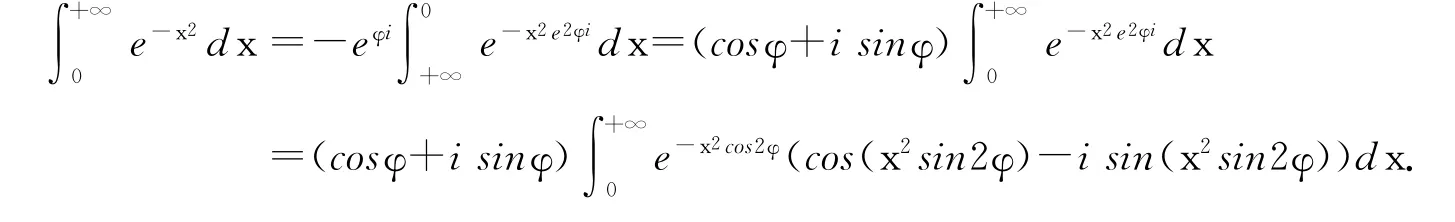
解之，即得

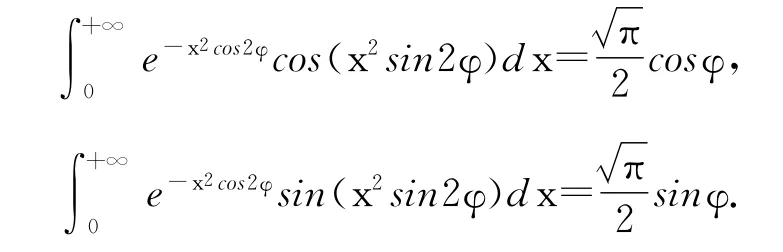
注 特别地，取φ＝π／4，即得著名的Fresnel积分：

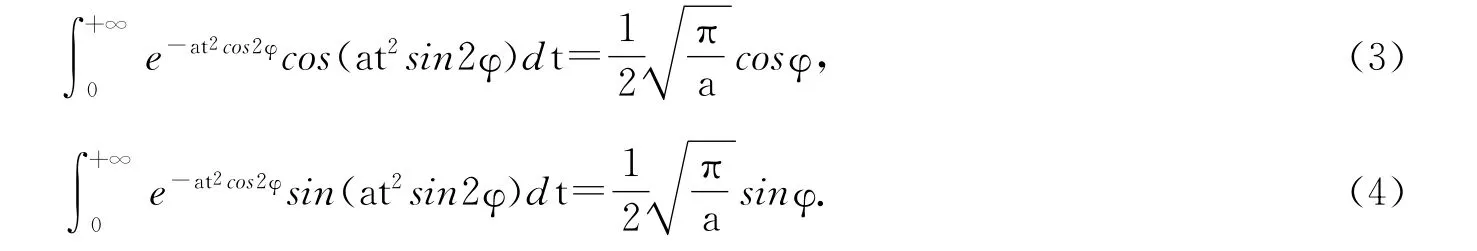
需注意，（3）式和（4）式中的φ应满足φ∈［0，π／4］．

将由上面两式证明比定理1．1更一般的结果．

定理1．2 设m≥0，n≥0，且m2＋n2≠0，则

证 令

2　进一步的推广

称为Γ函数，此积分对于任意x＞0都收敛．令t＝sα，α＞0，得

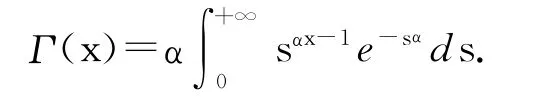
下面，进一步推广以上各个结果．为此，先介绍Γ函数的简单性质．反常积分

引理2 设α＞0，则

利用（7）式，有下述结果．

证 考虑函数

设γ是图2所示的闭曲线，把γ分为若干部分，其中γR和γr都是中心在原点，圆心角为φ的圆弧，而它们的的半径分别为R和r．函数f（z）在γ所围成的闭区域内解析，因此有

图2

即

下面，证明

设ρ＞0，有

上面的估计使用了引理1．因α－1＞0且

分离实部和虚部，并利用引理2，得

解之，最终得到

，得到比Fresnel积分更一般的结果

可得到与以上两式等价的结果

用类似于定理1．2的方法，可得到本文最具普遍性的结果之一．定理2．2 设m≥0，n≥0，α＞1，且m2＋n2≠0，则

不再赘述上面两式的证明．

由此易知ρ→＋∞和ρ→0时，（11）式右边均趋于0，这样，可以得到类似于定理2．1的结果．

定理2．3 设，则

注 特别地，在定理2．3中，取α＝1／n，n为正整数，并利用熟知的公式Γ（n）＝（n－1）！，可得到下述漂亮的结果．

当n＞1时，在上两式中还可取φ＝π／2，这样又得到

推论2．5 设n为大于1的正整数，则

同样地，由定理2．3并按照与定理1．2相同的论证方法，还可以得到类似于定理2．2的结果．

定理2．6 由m＞0，n≥0，且0＜α≤1，则

这里0≤φ＜π／2α且满足

注 上述定理中的m不能为0，否则φ＝π／2α，定理2．3不成立，上述定理自然也不成立．

至此，通过使用复分析方法，我们已经对Fresnel积分进行了多方面的推广．在进行推广的过程中，还得到了若干有趣的结果，这些结果用其它方法是很难计算的．实际上，许多著名的实积分，通过使用复方法都能得到推广．由此，我们可以看到，一些看似困难的数学问题，一旦使用强大的数学工具，就能轻松解决甚至作出推广．

［参 考 文 献］

［1］ 康威．单复变函数［M］．吕以辇，张南岳译．上海：上海科学技术出版社，1985．

［2］ 钟玉泉．复变函数论［M］．3版．北京：高等教育出版社，2004．

［3］ 菲赫金哥尔茨．微积分学教程（第二卷）［M］．8版．徐献瑜，冷生明，梁文骐译．北京：高等教育出版社，2006．

［4］ 叶鹏．Dirichlet积分的推广［J］．湖北师范学院学报，2002，22（1）：95－98．

A Further Generalization of Fresnel Integrals

ZHONG Wen－ti
（School of Mathematical Sciences，South China Normal University，Guangzhou，510631，China）

Abstract：Some improper integrals are calculated by using method of function of one complex variable．The results we obtained generalize Fresnel integrals．

Key words：improper integrals；Fresnel integrals；Cauchy＇s theory；Gamma function

［收稿日期］2015－09－30

［中图分类号］O174．5

［文献标识码］C

［文章编号］1672－1454（2016）01－0077－06