梁侧锚固钢板加固混凝土梁的横向剪力传递模型*

李凌志, 姜常玖, 陆洲导, 苏启亮

(1.同济大学 结构工程与防灾研究所，上海　200092；2.香港大学 土木工程系，香港)



梁侧锚固钢板加固混凝土梁的横向剪力传递模型*

李凌志1†, 姜常玖1, 陆洲导1, 苏启亮2

(1.同济大学 结构工程与防灾研究所，上海200092；2.香港大学 土木工程系，香港)

摘要：为研究梁侧锚固钢板加固钢筋混凝土梁(BSP梁)中钢-混凝土连接界面上的横向滑移对加固梁的极限承载力及变形性能的影响，将BSP梁中横向剪力传递类比于Winkler弹性地基模型，并结合已有试验和数值模拟成果，提出了可用于计算横向滑移和横向剪力传递的分段线性简化模型.从而得出了由混凝土梁和钢板抗弯刚度及螺栓连接剪切刚度计算横向滑移和横向剪力传递的实用计算方法.该简化模型的适用性得到了试验成果的检验，并可用于指导BSP梁的加固设计.

关键词：钢筋混凝土;梁侧锚固钢板;横向滑移;剪力传递;Winkler弹性地基模型

对于既有结构中承担振动、冲击和地震等动力荷载的钢筋混凝土梁，除了极限弯矩以外，延性和耗能能力也是最重要的考察指标.即使对非直接承受动力荷载的楼面梁，其达到极限承载力时具有足够的变形能力(如挠度、塑性铰转角等)，也能起到预警作用从而使梁能得到及时的维护加固，防止突然发生坍塌而危及生命财产安全.因此，当既有结构中的钢筋混凝土梁需采取加固措施时，除了极限弯矩以外，变形和耗能能力也是必须考虑的因素.传统的增大截面法虽然能同时提高强度和变形能力，但施工难度较大，而且由于楼层尽高限制往往难以实现.粘碳纤维和粘钢等方法虽然在不显著增加构件尺寸的前提下可有效增强梁抗弯及抗剪承载力[1-2]，但是很可能使梁的变形和耗能能力极大下降，并在粘结界面上产生脆性的剥离破坏[3-4].采用植筋后锚固技术将钢板固定在梁上的方法，剥离破坏将得以有效避免[5-7].虽然将钢板固定在梁底可显著提高梁的极限弯矩，但是对于既有建筑中大量存在的配筋率较高的梁(受拉配筋率与界限配筋率之比大于2/3)，采用该方法进行加固却很可能使梁发生超筋破坏.而采用梁侧锚固钢板法(Bolted-Side-Plating，BSP)在同样能提高梁极限弯矩的同时，还能保持延性以及增加抗剪承载力[8-9].

由于BSP法加固梁(Bolted-Side-Plated Beam)通过螺栓连接来实现钢板与混凝土梁之间的剪力传递以达到两者的共同工作，因此螺栓连接的剪切刚度(km)越大，连接界面上的剪切滑移越小，两者共同工作程度也越好[10].在分析中，剪切滑移可以分解为沿梁轴线的纵向滑移(Slc)和垂直于梁轴线的横向滑移(Str)，如图1所示.横向滑移(Str)产生的原因是螺栓在传递的横向剪力(简称横向剪力传递vm)的作用下产生横向剪切变形而导致的.

图1　BSP梁中的纵向和横向滑移

与纵向滑移及纵向剪力传递已有较多的研究成果[11-14]不同，国内外目前对于横向滑移及横向剪力传递的研究还处于起步阶段.Oehlers等人[8]通过假定所有螺栓全部进入塑性状态，初步建立了横向滑移与锚栓性能之间的联系.在此理论基础上，Nguyen等人[15]建立了纵横滑移之间的关系式.Siu和Su[9, 16]等通过总结试验成果，建立了对称荷载作用下横向滑移的线性简化模型.Su和Li等[17-18]对BSP梁横向滑移进行了试验观测和数值模拟，得到了横向滑移沿梁跨的分布规律以及随外荷载增长的发展规律.

虽然国内外学者对于BSP梁中横向滑移的研究取得了一定成果，但是由于横向滑移的数值一般小于1 mm，精确的试验测量难度较大.而且由于影响横向滑移的因素众多，要提出完善的理论模型十分困难.因此，本文从BSP梁中横向剪力传递与Winkler地基模型的相似点出发，结合已有试验及数值模拟成果，提出分段线性简化模型，以期得出横向滑移及横向剪力传递的计算公式，用于BSP梁的加固设计.

1理论模型

1.1基于Winkler地基的横向剪力传递理论模型

根据Winkler地基模型，对于放置在半无限弹性体地基上的无限长弹性梁，如果在梁跨中作用一个集中荷载，在地基中引起的反力将集中在荷载作用点附近且方向向上，集中力分布的范围与地基梁及地基刚度有关.在距离集中荷载稍远的区域，地基反力将迅速减小而逐渐变为零.类似地，当集中荷载作用于半无限长梁端部时，引起的地基反力也仅分布在梁端附近的较小范围.

通过本文作者前期的试验及数值分析结果[6, 17]可知，在BSP梁中，混凝土梁与钢板之间的横向剪力传递也与Winkler地基模型类似.可以将钢筋混凝土梁类比为弹性地基梁，螺栓和钢板类比为弹性地基，如图2所示.虽然螺栓为间隔布置，但当螺栓数量达到一定程度的时候，将螺栓连接简化成连续介质在计算精度上能得到保证.当无限长BSP梁在集中力F作用下，在荷载作用点处的钢板中将产生由螺栓传来的横向剪力(方向向上，可称为正向剪力传递)，且该正向剪力传递集中于荷载作用点附近.不同的是，钢板无法像地基土一样将荷载传递到更深的土层，因此只能利用距离F较远的一段区域，将从混凝土梁传来的正向剪力再传递回去，从而达到钢板自身横向力的平衡.该传回混凝土梁的横向剪力传递可称为反向剪力传递，如图2(a)所示.同样地，BSP梁端部集中荷载作用的横向剪力传递与半无限长弹性地基梁的地基反力类似，如图2(b)所示.

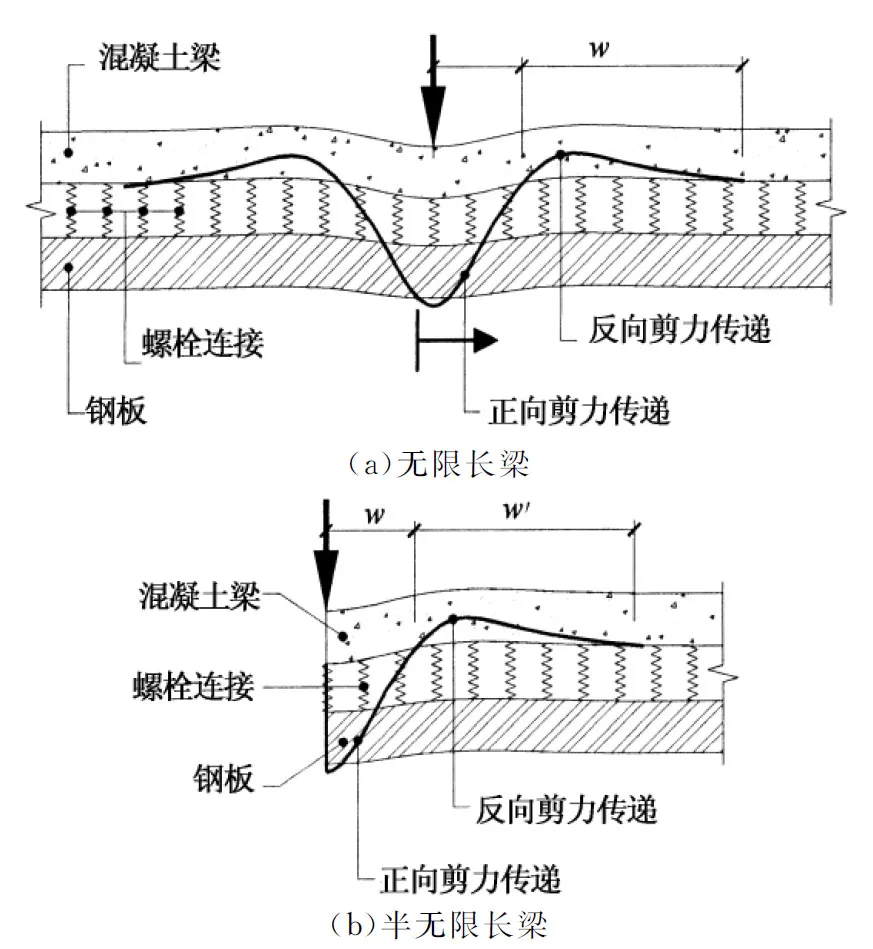
图2　BSP梁中横向剪力传递分布

由于BSP梁中承担横向剪力传递的螺栓连接的刚度是有限的，因此在钢板与混凝土梁之间将产生横向滑移Str.由于横向滑移的数值一般都较小，因此可假设螺栓的剪切变形为线弹性.以集中力作用点为坐标原点建立坐标系，类似于Winkler地基模型，可得横向滑移方程为：

(1)

式中: (EI)c为混凝土梁的弯曲刚度；k为由钢板与螺栓组成的等效弹性地基的等效刚度；q为外荷载引起的横向荷载.引入如下系数：

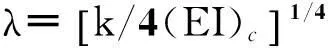
(2)

采用Hetenyi解析法[19]的通解：

(3)

由此可知横向滑移Str是一个周期为2π/λ的函数，最大值在集中力作用点处取得：

Str,max=Fλ/2k.

(4)

并且在如下位置取得第一个零点：

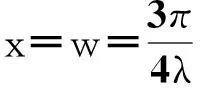
(5)

在下面的讨论中，我们将集中力作用点与零点之间的距离w定义为横向剪力传递的半带宽，从式(5)可以看出，w的大小仅决定于钢板、混凝土梁及螺栓连接的相对刚度(体现于λ)，而与外荷载F的大小无关.从式(3)可以看出，当某点与集中力的距离大于2w时，该处横向滑移的数值已经迅速衰减到小于Str, max的1%.由此可见，集中力引起的横向滑移仅集中在作用点附近的较小区域，超过2w之外的区域无需考虑，因此无限长梁的计算结果可以很方便地应用于有限长梁.当有多个外荷载作用时，利用叠加原理即可求解.由于均布荷载可看作是集中荷载的集合，集中弯矩可以看作一对等值反向的力偶而转化为集中荷载，因此均可运用上述公式和叠加原理进行计算.对于BSP梁支座，可采用半无限长梁计算结果(文献[19])并取反向即可.将支座和跨中外荷载作用下的计算结果叠加，即可求得整根梁的横向滑移.

虽然应用上述公式可以很方便地进行求解，但是与弹性地基梁中已知地基刚度不同，BSP梁中等效地基的等效刚度k与钢板几何尺寸(宽度和厚度)及螺栓连接属性(直径和间距)均有关系，目前尚无法得出基于理论的解析公式.为了解决这一难题，本文采用试验与数值计算结果相结合的方法，提出了如下简化分段线性剪力传递模型.

1.2基于试验及数值成果的横向剪力传递简化模型

本文作者前期进行了4根BSP梁的四点加载试验[18]，试件加固措施及加载装置如图3所示，试验中测得的其中两个加固试件P250B300R和P250B450R的横向滑移分别如图4(a)和图4(b)所示.由图4可知，随着加载水平从F/Fp= 0.25增加到0.75，由集中力外荷载引起的横向滑移的分布范围(即前文所说的半带宽w)都是保持不变的，这也通过试验实测验证了公式(5)的正确性.

图3　试件加固措施及试验加载示意图

图4　不同荷载水平BSP梁横向

此外，本文作者还采用有限元分析软件ATENA对不同荷载形式作用下BSP梁的横向滑移及横向剪力传递进行了深入分析，具体分析过程可参考文献[17].图5显示了三点及四点受弯时BSP梁横向剪力传递的分布曲线.由图5可知，横向剪力传递可近似地用多段折线表示，亦即可用一分段线性函数表示.因此为了较方便地求得BSP梁的横向滑移及横向剪力传递的分布，本文提出了如下简化模型(如图6所示)：

1)螺栓连接所传递的剪力与螺栓的剪切变形为线弹性关系，即

vm=kmStr．

(6)

2)混凝土梁和钢板的弯曲变形各自服从平截面假定.

3)跨中集中力作用下，横向剪力传递的形状为一等腰三角形.当相邻两个集中力的距离很近时，重叠区域的横向剪力传递叠加效应可忽略.

4)支座反力作用下，横向剪力传递的形状为一方向相反的直角三角形.

下面以四点受弯梁为例，说明如何应用上述简化模型来求解BSP梁中横向滑移及横向剪力传递.四点受弯梁的简化模型如图7所示，外荷载作用点处的横向剪力传递可表示为两个底边长为2w，高为vm,p的等腰三角形，支座反力处的横向剪力传递可表示为两个高为vm,s的直角三角形.由于对称性，只需计算半跨即可，因此横向剪力传递vm的表达式可由如下分段线性函数表示．

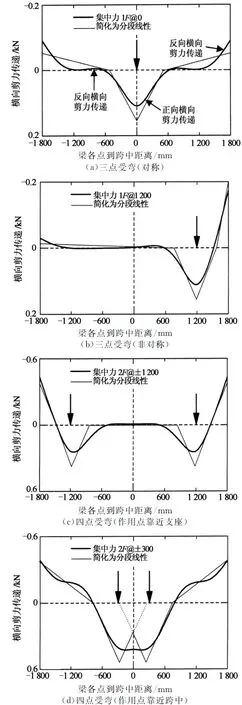
图5　不同形式集中力作用下BSP梁的横向剪力传递

图6　BSP梁中横向滑移及横向

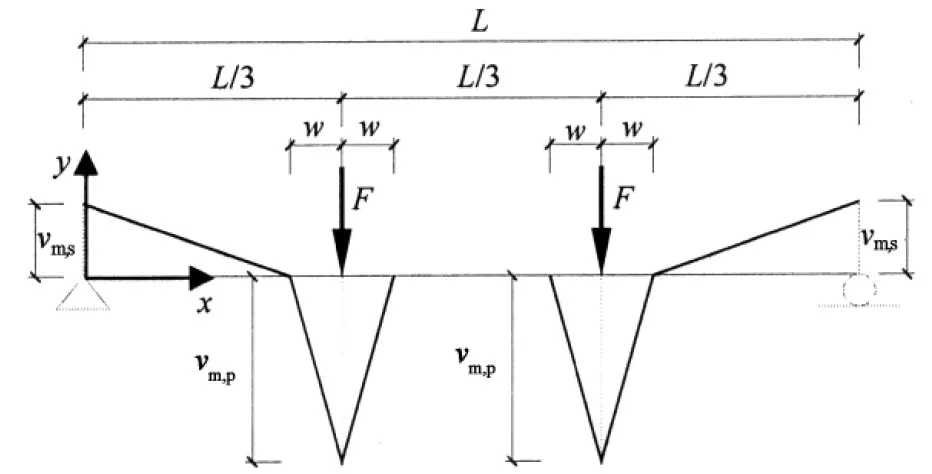
图7　四点受弯BSP梁横向剪力

(7)

由式(7)可知，vm仅由3个待定常数ξS,ξF和ξw确定.由于钢板仅受vm作用，因此利用其横向荷载平衡条件，可消去一个待定常数ξS：

(8)

既然混凝土梁的横向荷载(即外荷载加上vm)和钢板的横向荷载(即vm)均已确定，根据平截面假定即可求解混凝土梁和钢板的挠曲线(δp和δc)：

(9)

(10)

(11)

Apf=

将两者相减再加上如下端部相对滑移(可由钢板平衡条件求得)：

(12)

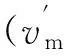
(13)

(14)

(15)

由式(15)可知，通过求解该一元六次方程即可求得ξw，然后代入式(14)即可求得ξF.再将ξw代回式(8)即可求得横向剪力传递(vm).

2试验验证

为了验证本文所提出的BSP梁横向滑移及横向剪力传递理论模型的适用性，本文将理论计算结果与作者前期试验研究[18]所得实测数据进行了对比分析，结果如图8和图9所示.

由图8可知，对于同一根梁P100B300，在荷载水平从F/Fp= 0.25增加到0.5再到0.75的整个加载过程中，理论计算结果与试验结果均相当接近.因此说明上述简化模型对准确计算横向剪力传递随整个加载过程的发展都是可行的.

由图9可知，除了上述P100B300试件以外，对于本次试验的其他试件(P100B450,P250B300R和P250B450R)，本文所提出的简化模型的计算结果与试验实测数据也是吻合的.

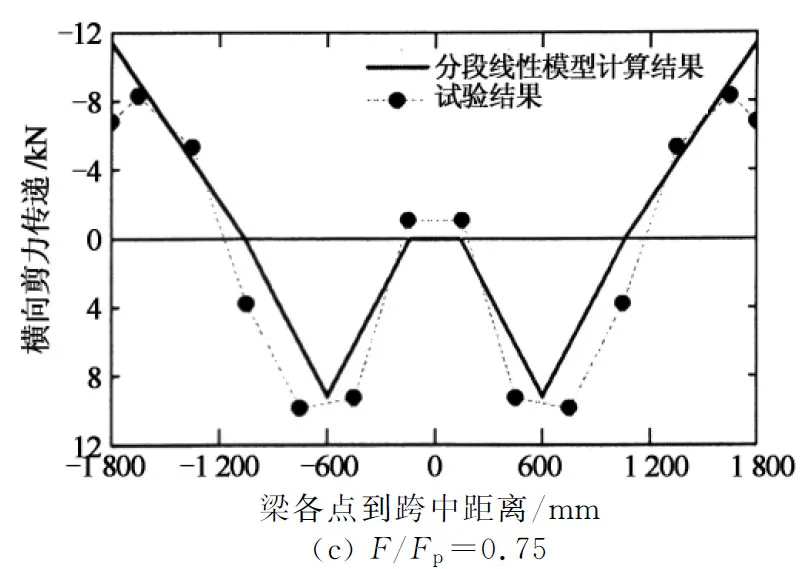
图8　不同荷载水平BSP梁横向

图9　同一荷载水平(F/Fp = 0.5)不同BSP梁横

3结论

本文从BSP梁中横向剪力传递与Winkler地基模型的相似点出发，分析了影响BSP梁中横向剪力传递的影响因素，并通过总结已有数值模拟结果将其简化为分段线性模型，成功地得出了横向滑移及横向剪力传递的近似计算公式.通过上述分析可得如下结论：

1)横向剪力传递的分布范围及其曲线形状与外荷载的大小无关，外荷载大小仅决定横向剪力传递曲线的绝对值大小.

2)由于横向滑移的数值较小，螺栓连接的横向剪切变形可认为符合线弹性假定.

3)跨中集中力作用下的横向剪力传递可简化为等腰三角形，支座反力作用下的横向剪力传递可简化为方向相反的直角三角形.

4)当相邻荷载距离较近时，重叠区域的横向剪力传递叠加效应可忽略不计.

5)通过与既有试验研究成果进行比较，本文所提出的简化模型能准确地预估BSP梁在整个加载过程中横向剪力传递沿梁跨的分布以及随外荷载增大的发展规律.

6)本文所得到的计算公式可用于BSP梁加固设计以考虑横向滑移对梁加固性能的影响，因而具有较好的工程指导意义.

参考文献

[1]尚守平, 李知兵, 彭晖. 碳纤维板-混凝土界面黏结性能的试验研究与有限元分析[J]. 湖南大学学报：自然科学版，2014, 41(6): 43-51.

SHANG Shou-ping, LI Zhi-bing, PENG Hui. Experimental research and finite element analysis of the interfacial bonding behavior of CFRP-concrete interface[J]. Journal of Hunan University: Natural Sciences, 2014, 41(6): 43-51. (In Chinese)

[2]张宇, 李思明. 粘钢加固钢筋混凝土梁可靠性分析 [J]. 湖南大学学报: 自然科学版, 2005, 32(6): 11-14.

ZHANG Yu, LI Si-ming. Reliability analysis of reinforced concrete beams strengthened with steel plates[J]. Journal of Hunan University: Natural Sciences, 2005, 32(6): 11-14. (In Chinese)

[3]DONG Y T, ANSARI F, KARBHARI V. Fatigue performance of reinforced concrete beams with externally bonded CFRP reinforcement[J]. Structure and Infrastructure Engineering, 2011, 7(3): 229-241.

[4]王晓刚, 李森, 周新刚. 有弱界面的CFRP抗弯加固中U型箍防剥离研究[J]. 土木建筑与环境工程, 2014，36(2)：14-20.

WANG Xiao-gang, LI Sen, ZHOU Xin-gang. Effectiveness of U-strips to prevent CFRP debonding in strengthened RC beams with weak interfaces[J]. Journal of Civil，Architectural & Environmental Engineering, 2014，36(2)：14-20. (In Chinese)

[5]BARNES R A, BAGLIN P S, MAYS G C,etal. External steel plate systems for the shear strengthening of reinforced concrete beams [J]. Engineering Structures, 2001, 23(9): 1162-1176.

[6]SU R K L, ZHU Y. Experimental and numerical studies of external steel plate strengthened reinforced concrete coupling beams[J]. Engineering Structures, 2005, 27(10): 1537-1550.

[7]李英民, 韩大刚, 林文修. 锚栓钢板加固法抗弯性能试验及设计方法[J]. 工程抗震与加固改造，2006, 28(5): 68-71.

LI Ying-min, HAN Da-gang, LIN Wen-xiu. Experiment study of flexural strengthening reinforced concrete beams by bolting steel plates and design method[J]. Earthquake Resistant Engineering and Retrofitting, 2006, 28(5): 68-71. (In Chinese)

[8]OEHLERS D J, NGUYEN N T, AHMED M,etal. Transverse and longitudinal partial interaction in composite bolted side-plated reinforced-concrete beams[J]. Structural Engineering and Mechanics, 1997, 5(5): 553-563.

[9]SIU W H, SU R K L. Analysis of side-plated reinforced concrete beams with partial interaction [J]. Computers and Concrete, 2011, 8(1): 71-96.

[10]SIU W H. Flexural strengthening of reinforced concrete beams by bolted side plates[D]. Hong Kong: Department of Civil Engineering, The University of Hong Kong, 2009: 187-188.

[11]NEWMARK N M, SIESS C P, VIEST I M. Tests and analysis of composite beams with incomplete interaction[J]. Proceedings of the Society for Experimental Stress Analysis, 1951, 9: 75-92.

[12]KIM S H, CHOI J H. Approximate analysis of simply supported composite beams with partial interaction[J]. Advances in Structural Engineering, 2011, 14(6): 1197-1204.

[13]SU R K L, LI L Z, LO S H. Longitudinal partial interaction in bolted side-plated reinforced concrete beams[J]. Advances in Structural Engineering, 2014, 17(7): 921-936.

[14]邓燕华. 梁侧锚贴钢板加固钢筋混凝土梁抗弯性能实验与设计计算方法研究[D].南昌: 华东交通大学土木建筑学院, 2009: 53-58.

DENG Yan-hua. Experimental study on the flexural behavior of reinforced concrete beam strengthened with bolted side steel plate and its design methods [D]. Nanchang: School of Civil and Architecture Engineering,East China Jiaotong University, 2009: 53-58. (In Chinese)

[15]NGUYEN N T, OEHLERS D J, BRADFORD M A. A rational model for the degree of interaction in composite beams with flexible shear connectors[J]. Mechanics of Structures and Machines, 1998, 26(2): 175-194.

[16]SU R K L, SIU W H. Nonlinear response of bolt groups under in-plane loading[J]. Engineering Structures, 2007, 29(4): 626-634.

[17]SU R K L, LI L Z, LO S H. Shear transfer in bolted side-plated reinforced concrete beam [J]. Engineering Structures, 2013, 56: 1372-1383.

[18]LI L Z, LO S H, SU R K L. Experimental study of moderately reinforced concrete beams strengthened with bolted-side steel plates[J]. Advances in Structural Engineering, 2013, 16(3): 499-516.

[19]MIKLBOSIMRE H. Beams on elastic foundation:theory with applications in the fields of civil and mechanical engineering[M].Michigan: University of Michigan Press, 1946: 10-26.

Transfer Model of Transverse Shear in Bolted Side-plated Reinforced Concrete Beams

LI Ling-zhi1†, JIANG Chang-jiu1, LU Zhou-dao1, SU Ray Kai-leung2

(1. Research Institute of Structural Engineering and Disaster Reduction, Tongji Univ, Shanghai200092, China; 2．Dept of Civil Engineering,The Univ of Hong Kong, Hong Kong, China)

Abstract:To study the influence of the interfacial transverse slip between concrete and the steel plates of bolted side-plated (BSP) RC beams on the structural performance, a simplified piecewise linear model for estimating the transverse slip and transverse shear transfer was proposed in analogy of the transverse shear transfer with the Winkler's model of elastic foundation, combined with previous experimental numerical studies. Thus, the functional calculation method for transverse slip and transverse shear transfer was obtained from the flexural stiffness of the RC beam and steel plates, and the shear stiffness of the bolt connection. The simplified theoretical model was also validated by test results, and it can be used for strengthening design of BSP beams.

Key words:reinforced concrete; bolted side-plate; transverse slip; shear transfer; Winkler’s model of elastic foundation

中图分类号：TU375.1

文献标识码：A

作者简介：李凌志(1980-)，男，湖南平江人，同济大学助理教授†通讯联系人，E-mail: lilingzhi@tongji.edu.cn

基金项目：国家自然科学基金资助项目(51408436)，National Natural Science Foundation of China(51408436)；香港政府研资局资助项目(HKU7151/10E)

*收稿日期：2015-05-17

文章编号：1674-2974(2016)03-0113-07