基于多因素混合模型的运营期群桩轴力预测*

陈志坚，黄伟杰

(河海大学 地球科学与工程学院，江苏 南京　210098)



基于多因素混合模型的运营期群桩轴力预测*

陈志坚†，黄伟杰

(河海大学 地球科学与工程学院，江苏 南京210098)

摘要：结合桥梁深水群桩基础在运营期间的受力特征，研究了深水群桩基础基桩轴力混合模型的一般原理.提出了基于多种环境因素影响下群桩基础监测数据的运营期混合模型，利用有限元模拟与PSO-SVM统计方法在苏通大桥群桩基础中实现了混合模型的构建.为了方便比较，建立了径向基函数(RBF)人工神经网络模型，对比了混合模型与RBF模型的预测结果.研究表明，混合模型预测精度较高，在受力情况不同的3根基桩上都有较为稳健的预测能力，具有较强的泛化能力，混合模型可适用于深水群桩基础运营期轴力的预测.

关键词：有限元方法；深水群桩基础；运营期；混合模型；多因素；轴力预测

随着近年来中国基础建设事业的日益发展，规模越来越宏大的建筑物在工程实践中也越来越常见，超大型群桩基础在大型工程中也得到了更多的应用.对于许多关乎国计民生的大型工程，不仅应关注其群桩基础在施工期的安全稳定情况，而且其群桩基础在运营期的安全稳定性也应该得到足够的重视.在工程中对轴力或承载力建立预测模型时大体可分为3类[1]，即统计模型、确定性模型和混合模型.其中混合模型[2-3]介于统计模型和确定性模型之间，即混合模型中某些分量用确定性模型来描述，其余分量用统计模型来描述，使其具备统计性质，又可以反映群桩的物理力学工作状态.混合模型建模受时域限制较小，外延功能较强，在大坝安全预测预报中已得到较为广泛的运用.目前，工程界对桩基础进行轴力或承载力预测时大多采用的是统计模型预测方法[4-5]，仍未见有运用混合模型建立群桩轴力预测模型的相关研究.

本文利用苏通大桥的多因素原型监测数据，分析了进行超大型深水群桩基础运营期基桩轴力预测的特点，吸取了利用混合模型建立大坝安全预测模型的思路，引入考虑多影响因素的混合模型预测方法，建立了深水群桩基础基桩轴力的多因素混合模型.并且，还利用径向基函数(RBF)人工神经网络建立了运营期轴力的预测模型，对比了RBF神经网络模型与混合模型在运营期群桩轴力预测中的精度.

1多因素混合模型的构建

在体量庞大的群桩基础建设阶段，承台的设计刚度、桥墩选址、桩位布置与桩间距等设计因素对后阶段运营期的各基桩轴力分布有着十分深刻的影响.而在大型深水群桩基础的正常运营期间，由于上述设计因素已经定型，上部荷载变化不大，与建设期相比，基桩轴力的变化幅度较小，群桩基础的受力情况主要受多种环境因素影响.对于有高耸上部结构的桥梁深水群桩基础而言，影响基桩受力安全性的多环境因素主要为潮位、交通流量、水温和风速等.在运营期群桩轴力预测模型的构建中，不仅需要精确考虑同步观测到的多种环境数据，并且应选择更加精准的预测模型才能满足运营期轴力的预测要求.

1.1群桩轴力混合模型基本原理

在大坝安全监控领域中[6]，大坝任一点的变形都是在水压力、扬压力、泥沙压力和温度等荷载共同作用下的结果.大坝变形量δ(t)按其成因可分为3个部分：水压分量fH(t)、温度分量fT(t)和时效分量fθ(t)，表达式为：

δ(t)=fH(t)+fT(t)+fθ(t).

(1)

大坝混合模型[7-8]是结合大坝和地基的实际工作性态，用有限元方法计算荷载(如水压)作用下的水压分量，而温度分量与时效分量则采用统计模型的方法来计算，后与实测值进行拟合优化而建立的模型.

借鉴上述大坝变形预测混合模型的思想，在深水群桩基础基桩轴力混合模型的构建中，各时刻轴力值F(t)按其变化成因也可由潮位分量Fl(t),交通流量分量Ff(t),水温分量Ft(t),风速分量Fs(t)等因素构成，混合模型表达式可写为:

F(t)=Fl(t)+Ff(t)+Ft(t)+Fs(t).

(2)

1.2PSO-SVM在混合模型中的运用

在式(2)的4个效应分量中，潮位分量是在潮位变化引起的不同浮力作用下对应的轴力值.潮位所引起轴力变化的物理力学机理较为明晰，可以由有限元法计算不同时刻潮位对应的轴力，进而采用多项式回归拟合出潮位分量公式.这种关系可用一元多项式来描述，即

(3)

式中:αi为回归系数；H为潮位高程.

交通流量分量Ff(t),水温分量Ft(t),风速分量Fs(t)与深水群桩基础的基桩轴力值F(t)之间存在着较为复杂的非线性关系，可采用统计模型的方法进行分析.支持向量机[9]是建立在统计模型理论上的机器学习方法，其在解决小样本、非线性、高维数方面具有很强的能力.因为支持向量机惩罚函数C和K(xi,xj)核函数中参数γ对算法泛化能力和计算效率有很大影响，如果人为确定的话，具有很大的盲目性.粒子群算法[10](PSO)是1995年美国的Kennedy和Eberhar受鸟群觅食行为的启发提出的随机全局优化算法，粒子群优化算法的具体内容参见文献[11]，本文不再赘述.利用粒子群算法优化支持向量机的参数便可以建立起PSO-SVM模型，PSO-SVM模型本质上仍是基于机器学习的统计方法，可应用于多因素群桩混合模型的构建.

利用PSO-SVM统计方法建立起交通流量分量Ff(t),水温分量Ft(t),风速分量Fs(t)与轴力值F(t)之间的非线性关系，用Ff·t·s(t)来表示.通过结合有限元计算与PSO-SVM 模型两种方法，则群桩轴力多环境因素混合模型式(2)可以表示为:

F(t)=mFl(H)+nFf·t·s(t)．

(4)

式中:m为潮位分量回归系数，因潮位分量为确定性模型计算值，m可取为1;n为PSO-SVM统计模型分量回归系数.

2工程应用

2.1工程概况

苏通大桥是迄今世界第二大规模的斜拉桥，开工建设于2003年，直至2008年7月1日正式通车运营，苏通大桥的多环境因素原型监测[12]也同步进入了运营期安全监测阶段.大桥主塔主4#墩(北主墩)和主5#墩(南主墩)均采用131根直径为2.8 m(上段)/2.5 m(下段)的大直径、超长、变径钻孔灌注桩基础，塔墩基础为迄今世界最大规模的桥梁超大型群桩基础.由于桩基础处于复杂的深水环境，考虑到群桩基础环境因素的复杂性，为了保证超大型群桩基础的安全稳定性，开展了群桩基础安全监测.苏通大桥南北索塔墩基桩轴力监测系统皆由10根监测桩组成，其中主5#墩各监测桩布置有9个监测断面，共布置24套钢筋应力计、18套混凝土应变计和2套顶出式压力盒，且布置有水压力监测仪、水温监测仪以及索塔顶风速监测仪.本文采用主5#墩上游承台29#、临近系梁区的36#桩以及下游承台的68#边桩这3根监测桩-12.0 m高程断面(第一断面)从2013年1月1日00：00至2013年2月7日06:00的150组实测监测数据进行深入分析．上述3根桩的轴力时程曲线如图1所示，3根监测桩的分布位置如图2所示.

日期

图2　3根桩在主5#墩承台分布图

2.2混合模型建立

苏通大桥位于长江下游潮汐河段，最大潮差约4 m，而体积巨大的群桩基础承台位于长江水面附近，对于平面面积达5 600 m2的主墩基础，潮位每米涨跌引起的浮力变化约为56.0 MN.苏通大桥车流量在不同时刻变化显著，车辆荷载也是运营期轴力变化的影响因素之一.且桥位区的水温一年内变化幅度较大，温度波动范围为8°～30°，温度的变化对混凝土应变有显著影响.另外，由于主5#墩处的索塔为三百多米的高耸建筑，索塔所受的风荷载也是影响桩基础轴力不容忽视的因素.综合上述分析，在建立运营期混合预测模型时应考虑的多环境因素为潮位、交通流量、水温与风速.

2.2.1有限元计算潮位分量的拟合表达式

在有限元分析中建立的模型尺寸与实际一致，土体模型根据弹性力学的厚壁圆筒理论、有限元原理及工程经验，在竖直方向、横桥方向与纵桥方向计算范围分别取为200 m，300 m与150 m，模型三维效果如图3所示.

图3　群桩基础三维模型图

基桩与承台之间变形协调，且在荷载作用下不会相互脱离，因此在基桩与承台之间可以用绑定约束连接.基桩与土体之间变形不协调，发生相互错动滑移，故在其间设置接触面单元，其模型设为库伦摩擦模型.本文采用ABAQUS有限元软件进行计算分析，接触面法向刚度为2.5×108N/m，切向刚度为3.0×106N/m，摩擦角为20°，粘结力为8 kPa.桩身混凝土采用弹性模型，重度为24 kN/m3，弹模为33 GPa，泊松比为0.167，凝聚力取30 MPa，内摩擦角取37°.地基土的本构模型采用Duncan-Chang模型，Duncan-Chang模型模拟桩基的变形性状效果较好，它考虑了土体的弹塑性变形的特征，并能较好地反映应力路径对变形的影响.

由桥位区的地质资料显示：地基土共分为18个工程地质层.按现有的计算条件无法一一考虑，可以通过相似的原则进行土层的概化，简化后的土体参数如表1所示.其中压缩模量Es与变形模量Eo可按下列理论公式进行换算[13]：

(5)

式中:ν为土体泊松比.群桩基础模型有限元网格剖分如图4所示.

表1　地基土层计算参数

图4　群桩基础模型剖分网格

对于上述平面面积达5 600 m2的群桩基础模型，每米潮差能引起56.0 MN的浮力改变量.利用作用在承台顶端中心的均布力模拟上部恒载，利用作用在承台底面的面荷载改变来模拟浮力大小的变化，并分别按潮位高程-7.00,-5.00,-3.00,-1.00,0.00,1.00,3.00和6.00 m等8种工况计算3根监测桩-12.0 m高程断面的轴力值，轴力有限元计算值如表2所示.

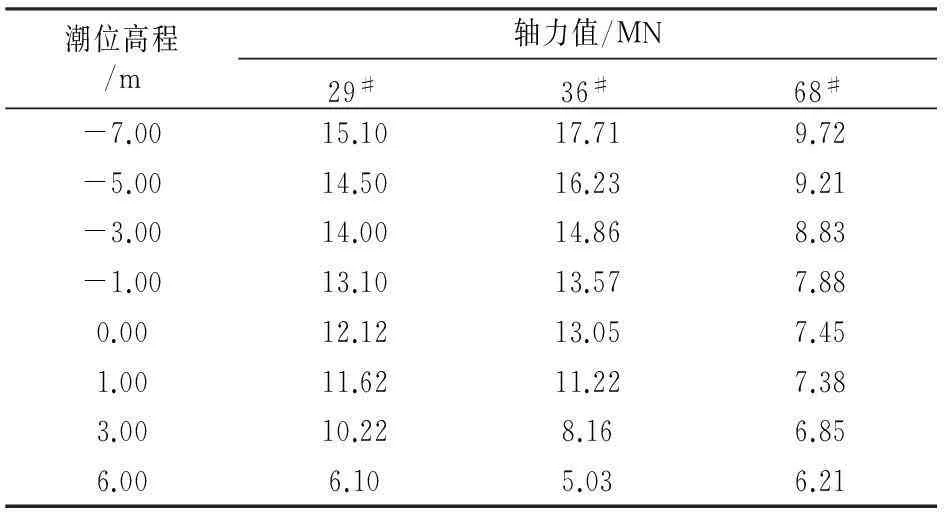
表2　不同工况下轴力值

由上述计算值，通过式(3)拟合潮位分量公式中的回归系数，确定各根桩的潮位分量公式分别为：

29#： Fl(H)=-0.043H2-0.759H+12.45；

(6)

36#：Fl(H)=-0.039H2-1.027H+12.42；

(7)

68#： Fl(H)=0.002H2-0.29H+7.61．

(8)

2.2.2其他分量Ff·t·s(t)统计模型建立

因样本数据量过大，本文仅展示其中29#监测桩运营期部分原型监测数据如表3所示.利用式(6)，式(7)和式(8)，可将表3中潮位对基桩轴力的影响进行剥离，剥离后的轴力可以认为是只受其他分量(交通流量、水温和风速)影响的轴力，剥离潮位影响后的29#桩原型监测数据如表4所示.利用表4中的数据，采用MATLAB编写的PSO-SVM程序，构建除潮位分量之外的其他分量Ff·t·s(t)与轴力之间的统计模型.

2.2.3确定混合模型回归系数

采用29#,36#与68#基桩从运营期2013年2月2日12：00至2013年2月4日18:00的10组监测数据为回归样本.利用上述建立的潮位分量Fl(H)公式与其他分量Ff·t·s(t)统计模型，分别计算3根桩的分量值如表5所示.利用MATLAB软件进行最小二乘法计算回归系数，可分别求出式(4)中3根桩对应的分量回归系数n，3根桩多环境因素轴力预测混合模型建立如下：

29#： F(t)=Fl(H)+0.586Ff·t·s(t)；

(9)

36#： F(t)=Fl(H)+0.215Ff·t·s(t)；

(10)

68#：F(t)=Fl(H)+0.855Ff·t·s(t)．

(11)

表3　29#桩实测数据汇总

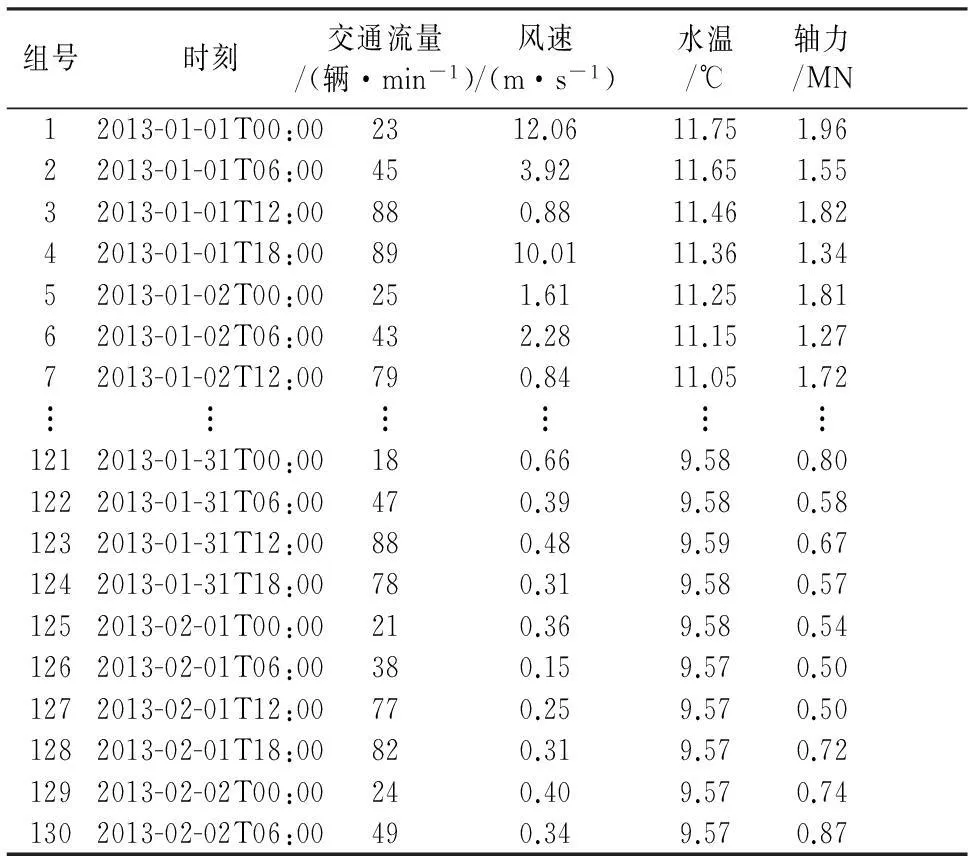
表4　剥离潮位影响的29#桩监测数据

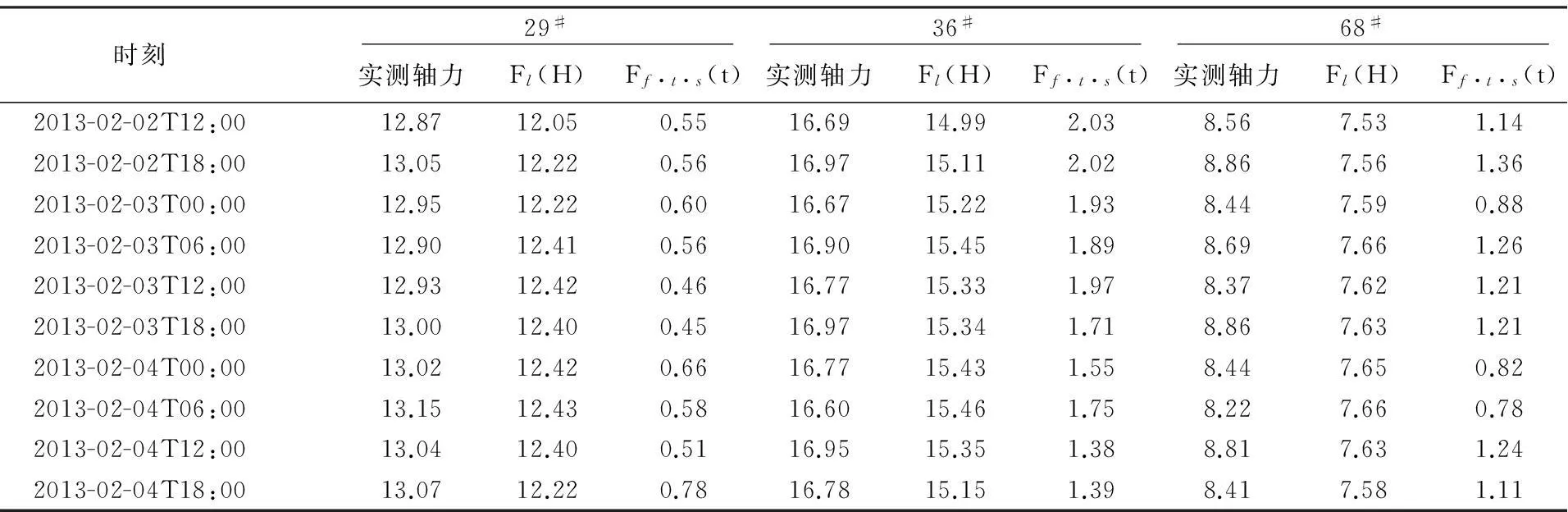
表5　轴力实测值与效应分量计算值

2.3预测结果对比分析

为方便对比，利用MATLAB建立了多因素RBF神经网络轴力预测模型，将潮位、交通流量、水温、风速等4个分量都做为RBF模型的考虑因素.

基于本文建立的混合模型与用于对比的RBF模型，分别对3根基桩从2013年2月5日00：00至2013年2月7日06:00的10组数据进行轴力预测，两个模型关于轴力实测值与预测值的对比结果如表6所示.各监测桩轴力两个预测模型的实测值与预测值相对误差统计图如图5所示.

混合模型与RBF模型的预测效果显示，在深水群桩基础的运营期轴力预测中，混合模型的预测精度高于径向基型(RBF)人工神经网络模型，能较好地对基桩轴力进行精确地预测.在分布位置不同、轴力变化情况各异的3根基桩轴力预测中，混合模型的平均百分误差(MAPE)为1.25，体现了混合模型出色的泛化能力与模型稳健性，较低的MAPE值也反映了混合模型能更好地满足运营期轴力预测对精度的要求.

组号

MN

3结论

1)在大型桥梁的通车运营期间，由于没有工程施工的影响，上部荷载较为稳定，桥梁群桩基础安全稳定主要取决于环境因素对基础的影响.因而探明影响群桩基础基桩轴力变化的因素，并分析各因素对轴力的影响特征是进行运营期轴力预测的关键.

2)在苏通大桥群桩运营期轴力原型监测中，潮位、交通流量、水温与风速是影响轴力改变的主要因素.其中潮位分量Fl(H)用有限元计算来确定，其他分量Ff·t·s(t)用PSO-SVM统计方法来确定，从而构建了多因素的混合模型，实现了对群桩轴力较为精准的预测.经过与RBF模型对比，展现了混合模型在运营期轴力预测中具有较高的精度、较好的泛化能力与模型稳健性.

3)多因素混合模型是基于大量的实测数据来进行构建的，类似工程中若实测数据量较少，可相应减少PSO-SVM的统计训练样本，按实践经验，50组的实测数据就能实现混合模型的构建.研究表明，有限元确定性模型对潮位分量实现了较好的拟合，可知确定性模型能胜任物理力学关系较为明晰的预测模型构建.因此在上部荷载大幅变化的建设施工期，若类似工程并无实测数据，确定性模型也是实现轴力预测的良好选择.多因素混合模型在本工程实例中的良好表现，反映了该模型考虑的环境影响因素符合工程运营期的实际工况，也验证了混合模型在群桩轴力预测中的可行性，在类似高桩深水大承台的群桩运营期轴力预测中，具有一定的工程应用价值.

参考文献

[1]彭虹, 史宇澄. 大坝监测资料分析模型的研究[J]. 大坝与安全, 1990(1):61-79.

PENG Hong, SHI Yu-cheng. Analysis model study of large dam monitoring[J]. Large Dam and Safety, 1990(1):61-79.(In Chinese)

[2]黄锋, 尹俊勋. 一种改进的基于GMM模型的语音序列评分和分类方法[J]. 湖南大学学报：自然科学版, 2008, 35(11):79-82.

HUANG Feng, YIN Jun-xun. An improved GM M-Based method for scoring and classification of speech sequence[J]. Journal of Hunan University:Natural Sciences, 2008, 35(11):79-82.(In Chinese)

[3]包腾飞, 吴中如, 顾冲时. 基于统计模型与混沌理论的大坝安全监测混合预测模型[J]. 河海大学学报：自然科学版, 2003, 31(5):534-538.

BAO Teng-fei, WU Zhong-ru, GU Chong-shi. Statistic model and chaos theory-based hybrid forecasting model for dam safety monitoring[J]. Journal of Hohai University:Natural Sciences, 2003, 31(5):534-538. (In Chinese)

[4]BYON S, NA D, LEE Y. Flow stress equation in range of intermediate strain rates and high temperatures to predict roll force in four-pass continuous rod rolling[J]. Transactions of Nonferrous Metals Society of China, 2013(3):742-748.

[5]董辉, 傅鹤林, 冷伍明,等. Boosting集成支持向量回归机的滑坡位移预测[J]. 湖南大学学报：自然科学版, 2007, 34(9):6-10.

DONG Hui, FU He-lin, LENG Wu-ming,etal. Boosting ensemble of support vector regression for landslide prediction[J]. Journal of Hunan University:Natural Sciences, 2007, 34(9):6-10. (In Chinese)

[6]吴中如. 混凝土坝安全监控的确定性模型及混合模型[J]. 水利学报, 1989 (5):64-70.

WU Zhong-ru. Concrete dam safety monitoring of deterministic model and hybrid model[J]. Journal of Hydraulic Engineering, 1989(5):64-70. (In Chinese)

[7]包腾飞, 吴中如. 混凝土裂缝开度混合预测模型[J]. 水利水电技术, 2005, 36(11):52-55.

BAO Teng-fei, WU Zhong-ru. A hybrid model for prediction of concrete crack opening[J]. Water Resources and Hydropower Engineering, 2005, 36(11):52-55. (In Chinese)

[8]WRAGG P D. Recent blooms of the dinoflagellate Ceratium in Albert Falls Dam (KZN): History, causes, spatial features and impacts on a reservoir ecosystem and its zooplankton[J]. Water SA, 2009, 35(4):455-468.

[9]VAPNIK V N. The nature of statistical learning theory[M]. New York: Springer-Verlag, 1995：35-68.

[10]SHI Y, EBERHART R C. Empirical study of particle swarm optimization[C]//Proceeding of Congress on Evolutionary Computation. Piscataway, NJ:IEEE Service Center, 1999:1945-1949.

[11]周驰, 高海兵, 高亮, 等. 粒子群优化算法[J]. 计算机应用研究,2003, 20(12): 7-11.

ZHOU Chi, GAO Hai-bin, GAO Liang,etal. Particle swarm optimization algorithm [J]. Application Research of Computers, 2003, 20(12): 7-11. (In Chinese)

[12]陈志坚, 薛涛, 冯凌云,等. 数据融合算法在苏通大桥群桩基础安全性评价中的应用[J]. 岩石力学与工程学报, 2009, 28:3270-3276.

CHEN Zhi-jian, XUE Tao, FENG Ling-yun,etal. Application of data fusion algorithm to safety evaluation of pile-group foundation of Sutong bridge[J]. Chinese Journal of Rock Mechanics and Engineering, 2009, 28:3270-3276. (In Chinese)

[13]高大钊. 土质学与土力学[M]. 3版. 北京：人民交通出版社, 2007：120-138.

GAO Da-zhao. Soil mechanics and soil science[M]. 3rd ed.Beijing：China Communications Press, 2007：120-138. (In Chinese)

Prediction of Axial Force in Pile Group during the Operation Period Based on the Mixed Model of Multiple Factors

CHEN Zhi-jian†，HUANG Wei-jie

(School of Earth Science and Engineering，Hohai Univ，Nanjing, Jiangsu210098, China )

Abstract:Combined with the stress characteristics of the bridge deep-water pile foundation during the operation period, this paper studied the general principles of the mixed model for pile axial force in deep-water pile foundation. The mixed model was firstly presented during the operation period based on the monitoring data of pile group foundation considering the influence of multiple environment factors. The mixed model of Sutong bridge pile group foundation was built by using the finite element simulation and PSO-SVM statistical method. In order to facilitate comparison, the Radial Basis Function (RBF) artificial neural network model was built, whose results were compared with the prediction results of the mixed model. The results showed that the mixed model had higher prediction accuracy and more robust predictive ability for the three piles under different loading conditions, and it exhibited better generalization ability. The mixed model could be applied to the prediction of the axial force in the deep-water pile group foundation during the operation period.

Key words:finite element method;deep-water pile group foundation;operation period;mixed model;multiple factors; axial force prediction

中图分类号：TU473.1

文献标识码：A

作者简介：陈志坚(1963-)，男，福建福清人，河海大学教授，博士生导师†通讯联系人，E-mail: zhijchen@hhu.edu.cn

基金项目：“十一五”国家科技支撑计划资助项目(2006BAG04B05)；国家重点基础研究发展计划(973计划)资助项目(2002CB412707)

*收稿日期：2015-04-06

文章编号：1674-2974(2016)03-0155-06