爆炸荷载作用下钢框架节点的动力响应分析
张秀华 李万成
(东北林业大学土木工程学院,黑龙江哈尔滨 150040)
爆炸荷载作用下钢框架节点的动力响应分析
张秀华李万成
(东北林业大学土木工程学院,黑龙江哈尔滨150040)
摘要:利用大型有限元软件ANSYS/LS-DYNA,对钢框架焊接节点在爆炸荷载作用下的动力响应进行了数值模拟,通过分析节点区位移时程曲线,得出节点在不同爆炸荷载作用下的动力响应特性,指出在爆炸荷载作用下,框架节点端部位移快速达到最大值,而后振动恢复至平衡位置,爆炸峰值压力越大,节点区梁柱最大位移和残余位移越大。
关键词:钢框架节点,爆炸荷载,动力响应,数值模拟
0 引言
近年来,各种类型的爆炸在世界各国频繁发生,爆炸冲击波作用对建筑结构会产生严重的破坏作用和很大的杀伤力[1]。因此,对结构的抗爆性能课题的研究在工程领域已逐渐成为一个重要的研究方向[2,3]。Sabuwala[4]等对边界完全固定的节点在爆炸荷载下做了有限元分析,分析结果指出了TM 5—1300规范对钢结构节点在爆炸荷载下的不足之处,并提出了修改建议。Urgessa[5]等对钢框架结构在爆炸荷载下做了有限元分析,对比了3种不同类型的节点动力响应,得出了3种节点的优缺点。Daryan[6]等对上下翼缘角钢连接的节点在爆炸荷载下做了有限元分析,讨论了在爆炸荷载作用下节点的破坏模式以及适用性。
本文采用显式动力分析软件ANSYS/LS-DYNA,研究钢框架焊接节点在爆炸荷载作用下的动力响应,为研究钢结构抗爆设计提供参考。
1 有限元模型的建立
1.1爆炸荷载作用下钢材的本构关系
钢材在常温静载情况下,所使用的本构关系一般不考虑应变速率的影响。但是在实际情况下,钢材的力学性能或多或少受应变速率的影响,特别是在受爆炸荷载等动载作用下,应变速率的影响非常显著[7]。本文钢梁和钢柱采用焊接工字型截面,钢材为Q345B,采用等向随动强化模型和Von-mises屈服准则。钢材按Cowper-Symonds方式考虑应变率效应对材料屈服强度的影响[8],见式( 1) :

其中,σd为动态屈服应力;σy为静态屈服应力;为等效塑性应变。具体参数取值见表1。

表1 材料参数表
1.2模型尺寸及相关参数
钢框架节点形式有多种,现在常用的钢框架节点形式,按受力特性分为:铰接、半刚性连接和刚性连接;按其加工工艺又可分为:全焊接连接、螺栓连接、铆钉连接和栓焊混合连接等[9]。本文采用焊接连接形式的节点为例,如图1所示建立有限元模型。本文所选框架结构的层高为3 m,柱网尺寸为6 m×6 m。钢梁和钢柱采用焊接工字型截面,单元类型采用Shell163单元,有限元模型如图2所示。

图1 钢框架节点模型图

图2 有限元模型
1.3荷载及约束条件
梁柱主要受力有:柱自重、梁上活载与恒载和爆炸荷载,在柱顶施加N =0.3Ncr=558 kN的竖向荷载,其中Ncr=1 860 kN,为柱子轴心受压稳定承载力,梁的上翼缘施加4 kN/m2的均布荷载,梁的上翼缘单元和柱的上部分翼缘单元施加爆炸荷载。并对柱顶端和底部加以水平滚动铰支座,梁端部加以竖向滚动铰支座。
爆炸荷载产生的冲击波很复杂,为了便于计算,研究人员对爆炸压力时程曲线做了不同形式的简化,本文采用简化成三角形冲击荷载形式,爆炸冲击波荷载表达形式为[10]:

式中: Ps——爆炸冲击波超压峰值;
td——爆炸持续时间。
2 计算结果分析
选取3种不同爆炸荷载,荷载1的超压Ps=2.5 MPa,冲量I = 30 MPa· ms;荷载2的超压Ps=5 MPa,冲量I =40 MPa·ms;荷载3的超压Ps=7.5 MPa,冲量I =50 MPa· ms。图3,图4分别给出了焊接连接节点区梁端部翼缘边缘的竖向位移时程曲线和柱端部翼缘边缘的水平位移时程曲线。
从图3,图4可以看出,随着爆炸荷载的施加,钢框架梁柱开始快速变形,梁柱最大位移几乎发生在爆炸荷载超压峰值之时。当爆炸荷载超压峰值和冲量较小时,梁柱端点位移快速达到峰值,而后恢复至平衡位置并在平衡位置振动,表现为弹性阶段;随着爆炸荷载超压峰值和冲量的继续增大,梁柱端点位移峰值不断增大,梁柱端点位移从峰值恢复至平衡位置后,仍有残余位移存在,表现为弹塑性阶段;继续增加爆炸超压峰值和冲量,梁柱端点位移快速达到最大值之后,梁柱端点位移峰值和残余位移比较接近,并且振动减弱,表现为塑性破坏阶段。

图3 梁端部翼缘边缘竖向位移时程曲线
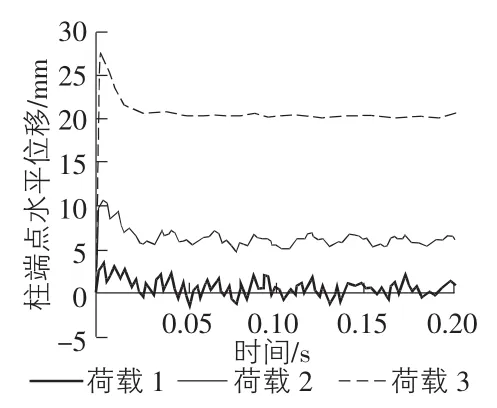
图4 柱端部翼缘边缘水平位移时程曲线
3 结语
利用ANSYS/LS-DYNA显示动力有限元分析软件,对焊接连接形式的节点在爆炸荷载作用下进行动力响应模拟分析,由节点的变形特点可以得出:
1)利用ANSYS/LS-DYNA有限元软件,能够很好地模拟爆炸荷载作用下钢框架焊接节点的动力响应,对节点进行动力分析是可行的。
2)在爆炸荷载作用下,节点区位移快速达到峰值,而后恢复至平衡位置,并在平衡位置振动。爆炸超压峰值和冲量越大,节点位移峰值和残余位移越大。
参考文献:
[1]汪明.爆炸荷载作用下钢结构损伤机理及砌体墙破碎过程研究[D].天津:天津大学,2010.
[2]张守中.爆炸基本原理[M].北京:国防工业出版社,1988.
[3]周听清.爆炸动力学及其应用[M].合肥:中国科学技术大学出版社,2001.
[4]Sabuwala T,Linzell D,Krauthzmmer T.Finite element analysis of steel beam to column connections subjected to blast loads [J].International Journal of Impact Engineering,2005,31( 7) : 861-876.
[5]Urgessa G S,Arciszewski T.Blast response comparison of multiple steel frame connections[J].Finite Elements in Analysis and Design,2011,47( 7) :668-675.
[6]Daryan A S,Ziaei M,Sadrnejad S A.The behavior of top and seat bolted angle connections under blast loading[J].Journal of Constructional Steel Research,2011,67( 10) :1463-1474.
[7]辛志强.爆炸与火灾联合作用下结构钢本构关系研究[D].沈阳:沈阳建筑大学,2012.
[8]John O Hallquist.LS-DYNA keyword user’s manual[M].Livermore California: Livermore Software Technology Corporation,2006.
[9]许建勋.钢框架节点受力性能及其对框架受力性能影响研究[D].杭州:浙江工业大学,2002.
[10]张秀华,张宇,段忠东,等.爆炸荷载作用下钢柱的动力响应与影响因素分析[J].防灾减灾工程学报,2014( 1) : 73-77,84.
The dynamic response analysis of steel frame joints subjected to blast loads
Zhang Xiuhua Li Wancheng
( College of Civil Engineering,Northeast Forestry University,Harbin 150040,China)
Abstract:The ANSYS/LS-DYNA software is used to set up the steel frame joints models and analyze the responses subjected to blast loads.The dynamic response characteristics of joints under different blast loads were obtained through analysis of displacement time history curves of joints.The paper points out that under blast loads,the joints displacement quickly reach the maximum value,and then decrease to the equilibrium position.The displacement maximum value and residual displacement of column and beam increase with the increase of blast loads.
Key words:steel frame joints,blast load,dynamic response,numeric simulation
作者简介:张秀华(1970-),女,硕士生导师,副教授;李万成(1990-),男,在读硕士
收稿日期:2015-11-22
文章编号:1009-6825( 2016) 04-0019-03
中图分类号:TU323.5
文献标识码:A

