梯形槽道微型平板热管的特性研究

金志浩，　代立鹏，　汤方丽，　赵常铭

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)



梯形槽道微型平板热管的特性研究

金志浩，代立鹏，汤方丽，赵常铭

(沈阳化工大学 能源与动力工程学院， 辽宁 沈阳 110142)

摘要:建立并完善具有梯形槽道的平板微热管的两相流稳态模型，着重分析管内汽液压力、弯月面半径的轴向变化，及弯月面接触角角度对热管传热量的影响，更全面考虑到汽液界面剪切作用和壁面摩擦的影响.研究了槽道深度值以及上下底长度比值对热管传热能力的影响，模型计算结果与实验研究数据对比较一致，并在现有研究基础上更精准.该模型为不同槽道形状的微热管理论模型研究提供了修正方法.

关键词：梯形槽道；平板热管；剪切力；传热能力

当前，电子电路不断向微小型化、高集成度、大规模方向迅速发展，随着集成电路功耗越来越大，芯片级散热要求甚至超过100 W/cm2.而温度恰又严重制约和影响着电子原件的正常运行，55 %以上的设备器件失效均由热引起.散热问题已经成为限制电子信息化发展的关键技术之一[1-2].传统冷却技术如风冷、液冷及热电制冷等已无法满足高性能芯片大热流密度的需求，普通热管因尺寸限制也不能适应，微型热管由于其体型灵活轻便，与电子器件易装配，传热效率高，温度均匀性好等突出性能而在微电子散热领域得到广泛应用和发展[3].

Cotter首先于1984年提出微型热管的概念[4].之后微型热管历经了具有矩形、三角形等截面的单根热管到微型热管阵列的结构转变，随后进一步产生微型多槽道平板热管.目前文献对三角形、矩形、Ω型、梯形形状沟槽均有研究[5-9]，通过理论建模和模拟分析较好地预测了微型平板热管的传热传质性能.但现有数学模型对于管内摩擦力影响均考虑不完善，本文基于前人研究，针对梯形槽着重研究壁面及汽液高速对流产生的界面摩擦对微热管性能的影响，重点分析管内压力变化.并仿真计算了梯形槽上下底长度比、槽道深度等变化对其传热量的影响，仿真结果与颜吟雪，范春利[10-11]等的研究结果相一致，表明本模型计算的准确性，并且为不同槽道形状的微热管理论模型研究提供了修正方法.

1两相流数学模型

本文研究的平板热管其内部梯形槽道横截面结构如图1所示.微型平板热管传热机理是利用内部流体循环往复地汽液相变，实现不间断地热量传送.但实际上其微结构内部两相流流动非常复杂，传热过程更涉及到热传导、热对流、热辐射.

图1中:H代表热管的蒸汽腔高度；h代表梯形槽道的高度；w1为梯形槽道的上底边长；w2为梯形槽道的下底边长；d为梯形槽道之间的间距距离.

为此，在保证计算精准度的前提下，必须对内部工作过程进行适当简化，建立必要的假设：

(1) 在稳态状态下工作，蒸发段与冷凝段均处于恒热流边界条件；

(2) 工作流体沿着轴向一维不可压缩层流流动，忽略管壁轴向热传导；

(3) 汽液界面的弯月面半径仅沿轴向变化，各变量在沿轴截面取平均值；

(4) 蒸发仅发生在汽液界面，液体沿着槽分布均匀，冷凝段无阻塞.

稳态模型利用有限容积法建立，将平板微热管沿长度方向分为若干控制体dz，针对单个控制体对汽液相建立方程.

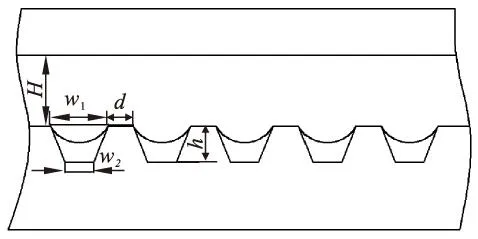
图1　梯形槽道平板热管截面示意图

1.1质量守恒方程

稳态条件下，控制体内液体和蒸汽质量的时间变化率为零.则对于梯形槽道内的汽体和液体分别有:

(1)

(2)

其中:N=ρuA，ρ为流体密度，u为流速，A为流体流通横截面积；vj,v和vj,l分别为汽液界面上汽相、液相工质的平均界面相变速率；yj为汽液界面有效长度；并且由于单元有限容积内汽液相变的质量连续，所以有ρvvj,v=-ρlvj,l.

1.2动量守恒方程

线性动量守恒在控制体内由重力部分、动量部分及剪切力等组成，本模型采用Navier-stokes方程描述工质的动量守恒:

gρvAvsinθdz+yv,bτv,bdz+yjτl,vdz

(3)

gρlAlsinθdz+yl,bτl,bdz+yjτv,ldz

(4)

其中:uv和ul分别为汽体、液体轴向速度；Av和Al分别为汽体、液体流动通道横截面积；pv和pl分别为汽体、液体轴向压力；θ为热管的水平倾角；yv,b和yl,b分别为汽体、液体的润湿周长.

流体剪切力计算基本公式:

(5)

对于壁面剪切力，摩擦系数[5]:

(6)

po=24(1-1.355 3cmin+

(7)

其中:po为泊肃叶数；cmin=(w1+w2)/2H为槽道形状系数；Dh=4A/P为流体流动区域当量水力直径，其中P为流体润湿周长.

对于液体和蒸汽高速反向流动造成的界面剪切力，将影响液膜厚度的分布，蒸汽受到界面摩擦的摩擦系数[8]:

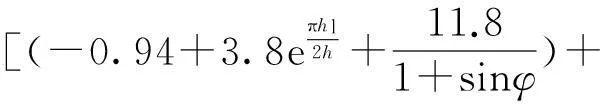
(8)

1.3能量守恒方程

假设蒸发段和冷凝段热量各自均匀变化，绝热段没有热损失.则界面速度表示为:

(9)

其中:Lj为流体流通长度；q(z)为单位面积横向热通量，q(z)=Q(z)/Ai，Ai为沿轴任一截面面积.轴向热负荷Q(z)分布如下:

(10)

其中:Qru为蒸发端输入热量;Le、La、Lc及Lall分别代表蒸发段、绝热段、冷凝段及热管总长度.

1.4Laplace-Young方程

平板微热管两端由于液膜厚度的变化而产生弯月面半径差，进而产生轴向毛细压差，驱动液态工质回流，如此往复循环.该方程给出了弯月面半径与汽液轴向压差的关系.

pv(z)-pl(z)=σ/r(z)

(11)

其中:σ为表面张力系数；r为液体弯月面半径.

1.5边界条件

在蒸发端z=0处，

re=re0;pv=psat;pl=psat-σ/r0;

ul=uv=0.

(12)

其中psat为运行温度下蒸汽饱和压力.

2数值分析结果与讨论

对方程(1)～(11)运用边界条件(12)采用四阶龙格库塔算法求解.模型所研究的平板微热管外形尺寸(长×宽×高)按63 mm×20 mm×7 mm计算，蒸发段、绝热段及冷凝段均20 mm，工作介质为水，充液率给定1.2，固液接触角按5°，在水平状态下计算.平板微热管槽道内的结构尺寸见表1.

表1　平板微热管梯形槽道结构尺寸

图2计算分析了槽深在0.5～1.0 mm范围内变化平板微热管最大传热量随温度的变化.由图2可以看出：在同一位置运行温度下，随着槽深的增大，平板微热管最大传热量不断提高.并且随着温度升高，平板微热管整体最大传热量均有升高，不同槽深最大传热量之间差距逐渐变大.这反映出深槽对传热有利，并且温度适当提高，有助于热管进入好的工作状态.

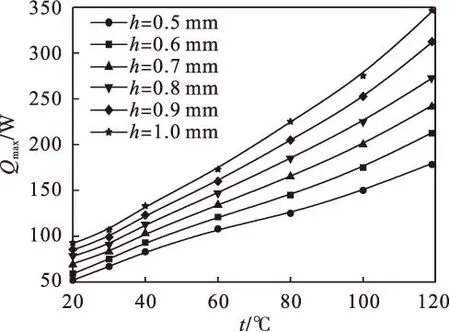
图2　不同工作温度下槽道深度对最大传热量的影响

令上下底分别在0.2～0.8范围内取值，得到不同上下底比值(w1/w2)，进而数值分析工作温度50 ℃时平板微热管上下底大小比值对最大传热量的影响，结果见图3.由图3可见：随着槽道上下底比值不断增大，最大传热量随之减小，两者近乎反比例变化.出现这种规律说明上底越短，下底越长，传热效果越好.因为这样槽道底角越小，尖锐的槽道底角能形成更大的毛细力，加速液体回流.

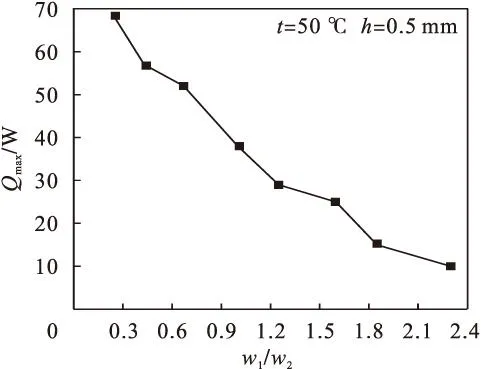
图3　槽道上下底边比对最大传热量的影响

从图2和图3的数据结果分析看出：本模型对于槽高，槽上下底边等结构尺寸对平板微热管传热能力影响的研究结果与颜吟雪,范春利[10-11]的实验结论取得一致，梯形槽道越深，上底越窄，下底越宽，传热能力越好.从而验证了本模型的可应用性.并且本文展开了对液汽及壁面剪切应力更为精细的研究.

在蒸发段端面弯月面接触角取不同角度情况下，研究不同剪切力对平板微热管的最大传热能力的影响，结果如图4所示.随着弯月面接触角的增大，平板微热管在3种剪切力情况下最大传热量均有整体减小趋势.在考虑剪切力影响时，汽液界面剪切力(τl，v)相比于无剪切力时，传热量大幅下降；壁面剪切力τb相比于无剪切力时，传热量有小幅下降.弯月面接触角对传热性能影响很大，接触角越小时，剪切力对传热能力影响越显著.弯月面接触角保持在5°到15°左右时，传热能力达到最佳水平.

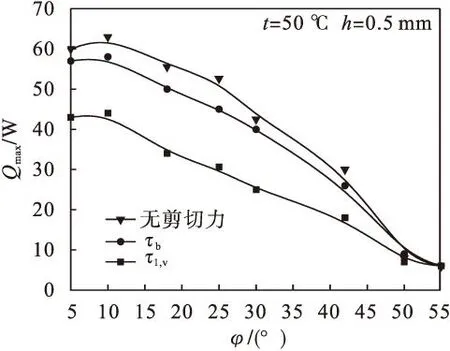
图4　不同接触角下剪切力对最大传热能力的影响

数值计算中，在温度t=50 ℃,导热量Q=65 W情况下，研究平板微热管在考虑不同剪切力作用下液体、汽体的压力轴向分布,如图5所示.该条件下，在研究整体压力走向时，管内蒸汽压力沿轴向缓慢下降，波动小；液体压力沿轴向变化较剧烈，不断上升，蒸汽压力沿整个轴向变化值仅占液体压力变化的30 %左右，且蒸汽、液体压力均在绝热段附近变化显著，进入冷凝段后，变化趋于平稳.随着弯月面曲率半径的增大，蒸汽和液体两者之间的压力差沿轴向不断缩小.

在比对不同剪切力对内部压力影响时，当考虑流体与壁面摩擦剪切力存在时，较理想的无剪切力情况比较，热沉与热源两端蒸汽压差、液体压差及蒸汽和液体两者之间的压力差均有小幅缩减；而当考虑汽液界面剪切力时，较其余两种情况比较，蒸汽压力差大幅减小，差值只有10 Pa左右，液体压差和汽液压差也迅速减小.两端压力差受摩擦阻力影响减小，进而使工质回流进程动力不足，影响热管内工作效率.由图5可看出：汽液界面剪切力对管内汽液循环的影响很大，不可忽略，而汽壁、液壁剪切力影响不大.

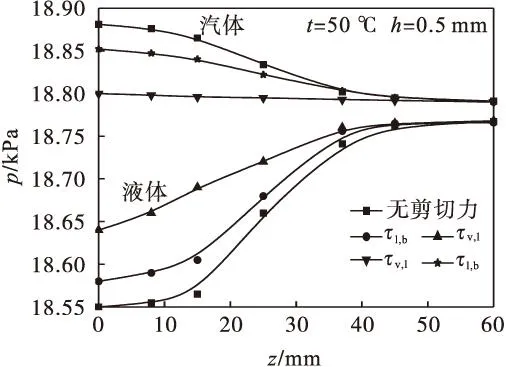
图5　不同剪切力下液体、汽体压力分布

平板微热管随着输入热流密度的增加，管内蒸发冷凝作用加剧，内部循环需要更大的毛细压力差来推动，而弯月面半径差正是产生毛细压力差的重要原因.因此，两者之间应具有一致的变化规律.针对输入热量为55、65和75 W三种情况进行了计算分析，结果见图6.

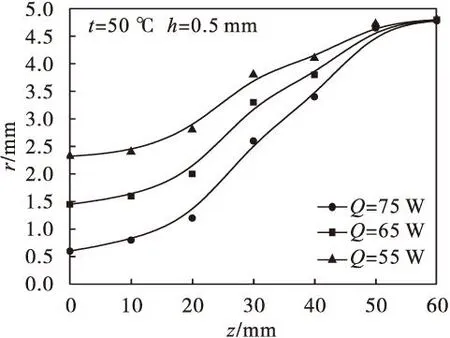
图6　不同热输入下弯月面半径的轴向分布

由图6可以看出：弯月面半径沿轴向分布与液体压力分布有相仿规律.随着输入热量的增加，蒸发段蒸发加强，弯月面半径不断减小.当实际工作中，管内热流密度更大时，液膜几近蒸发干，蒸发端弯月面半径将达到最小，而此时管内将到达工作极限.

平板微热管内部为复杂的两相换热，作为重要的导热元件，其传热能力的好坏是评定热管自身性能的关键指标.本文引入一种新的等效对流换热系数的方法来尽可能科学准确地评估热管的传热性能.

等效对流换热系数k的推导公式为：

(13)

其中：Av，l为平板微热管蒸发段面积；λ为管壁导热系数；A为平板微热管面积；tv为蒸发段外壁面温度;tc为冷凝段外壁面温度;δ为管壁厚度.

图7为在输入热量100 W以内，等效对流系数的变化曲线.在加热量小于80 W时，等效对流系数正比于加热量变化；当加热量超过80 W时，等效对流系数开始反比于加热量变化；加热量在80 W左右时，其等效对流系数最大，说明在此工况下，平板微热管的传热能力达到最佳水平.本文又运用传统的当量导热系数法计算，两种方法得出的平板微热管传热性能变化规律相似.

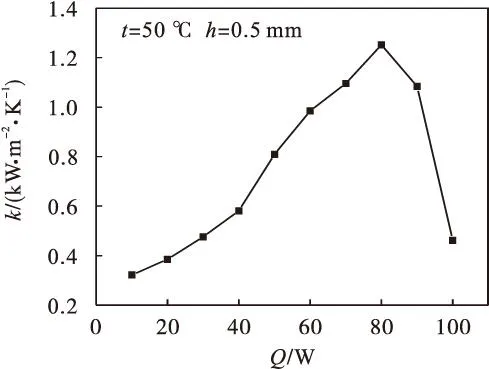
图7　不同加热量对等效对流换热系数的影响

3结论

本文通过对梯形槽道的平板微热管建立稳态的流动及导热模型，较全面考虑了汽液界面剪切力和壁面剪切力的影响，通过定结构参数，改变单一变量值的方法得出以下主要结论：

(1) 汽液界面剪切力对平板微热管的传热量影响很大，研究时必须考虑；壁面剪切力的影响较小.弯月面接触角在5°～15°左右时，传热能力最佳.

(2) 沿轴向液体压力变化较大，蒸汽压力变化小，蒸汽压力沿轴向变化值占液体压力变化值的30 %左右.液体压力整体变化趋势同弯月面半径一致.

(3) 等效对流换热系数可以用来评估热管的传热性能，在定工况下，可通过等效对流系数找到最佳工作功率.

参考文献：

[1]李庆友,王文,周根明.电子元器件散热方法研究[J].电子器件,2005,28(4):937-941.

[2]CHEIN R,HUANG G M.Thermoelectric Cooler Application in Electronic Cooling[J].Applied Thermal Engineering,2004,24(14/15):2207-2217.

[3]VASILIEV L L.Micro and Miniature Heat Pipes—Electronic Component Coolers[J].Applied Thermal Engineering,2008，28(4):266-273.

[4]COTTER T P.Pricipies and Prospects of Micro Heat Pipes[C].Tsukuba:Proc.5thInt.Heat Pipe Conf.,1984:328-335.

[5]LEFEVRE F,RULLIER R,PANDRAUDA G.Prediction of the Temperature Field in Flat Heat Pipes with Micro-grooves Experimental Validation[J].Heat and Mass Transfer,2008,51(15/16):4083-4094.

[6]刘晓为,辛欣,霍明学,等.微型多槽道平板热管传热特性分析及最大传热量预测[J].传感技术学报,2007,20(9):2103-2107.

[7]刘一兵.一种微矩形槽平板热管的数值模拟和有限元热分析[J].低温工程,2010(3):35-38.

[8]SUH J S,GREIF R,GRIGOROPOULOS C.Friction in Micro-channel Flows of a Liquid and Vapor in Trapezoidal and Sinusoidal Grooves[J].International Journal of Heat and Mass Transfer,2001,44(16):3103-3109.

[9]张程宾,施明恒,陈永平,等.“Ω”形轴向槽道热管的流动和传热特性[J].化工学报,2008,59(3):544-550.

[10]颜吟雪,李春林,赵振明,等.一种微型槽道热管的性能分析与试验研究[J].航天返回与遥感,2013,34(5):56-62.

[11]范春利,曲伟,孙丰瑞,等.三种微槽结构的平板热管的传热性能实验研究[J].电子器件,2003,26(4):357-360.

Characteristics of a Micro Flat Heat Pipe with Trapezoidal Grooves

JIN Zhi-hao,DAI Li-peng,TANG Fang-li,ZHAO Chang-ming

(Shenyang University of Chemical Technology, Shenyang 110142, China)

Abstract:A two-phase flow steady-state model of a micro flat heat pipe with trapezoidal grooves was developed and perfected,which emphatically analyzed the axial change of tube pressure between vapor and liquid,the meniscus radius and the influence of the degree of meniscus contact angle on heat pipe heat transfer.It comprehensively considered the influence of the vapor-liquid interface shearing action and wall friction.The influences of groove depth and the upper and bottom length ratio the heat transfer capability of heat pipe were studied.Model calculation results were consistent with experimental study theory,and more accurate on the basis of existing research.The model provided a correct method for theoretical model of micro heat pipe with different groove shape.

Key words:trapezoidal grooves;flat heat pipe;shear stress;heat transfer capability

中图分类号：TK172.4

文献标识码：A

doi:10.3969/j.issn.2095-2198.2016.01.012

文章编号：2095-2198(2016)01-0060-05

作者简介：金志浩(1964-)，男，浙江东阳人，教授，博士，主要从事热管传热特性研究.

基金项目：国家重点基础研究发展计划(2011CB706504)

收稿日期：2014-10-23