基于误差补偿的谷氨酸发酵过程模型预测控制研究

关长亮，　王贵成

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)



基于误差补偿的谷氨酸发酵过程模型预测控制研究

关长亮，王贵成

(沈阳化工大学 信息工程学院， 辽宁 沈阳 110142)

摘要:谷氨酸发酵过程是一种具有高度的非线性、强烈的时变性和大滞后等因素的生化过程.本文将神经网络和预测控制算法相结合，用于解决谷氨酸发酵过程非线性控制问题.首先，通过神经网络实现非线性模型的预测能力；然后，引入动态矩阵控制，建立基于误差补偿的谷氨酸神经网络预测系统，通过滚动优化﹑反馈校正﹑误差补偿进行多步预测，最终构建谷氨酸发酵过程多变量非线性控制系统.仿真结果表明：该方法能够实现对谷氨酸发酵非线性过程的有效控制.

关键词：谷氨酸发酵过程；非线性系统；神经网络；多变量;动态矩阵控制

发酵过程由于其本身特殊的动力学特征区别于一般的物理和化学过程，如动力学模型呈现一定的滞后性和高度的非线性以及强烈的时变性等因素.因此，发展和建立与发酵过程的特点相适应、具有共性的发酵过程建模、控制与优化技术，对于提高发酵过程的总体性能，提高目的产物的产率、产量、生产强度记忆以及原料的转化率，起到至关重要的作用[1].从20世纪中期开始，发酵过程控制体系一直采用传统的 PID 方法.如今，在大多数的工业现场控制中，由于传统的 PID 控制简单灵活并且价格相对低廉，动静态特性基本可被大多数精度要求不高的工业生产所接受.但对于像谷氨酸发酵过程这种被控过程复杂、具有高度非线性、时变不确定性和纯滞后等特点的系统，传统的PID 控制将难以取得令人满意的控制效果[2]，因此，将非线性预测控制算法应用到发酵过程控制中，对提高发酵系统的速率、提升产品质量、增加社会经济效益具有广泛影响.本文研究一种基于误差补偿的神经网络预测控制算法，应用于谷氨酸发酵过程，对提高谷氨酸产量进而提高企业的效益具有一定意义.

1谷氨酸发酵过程介绍

1.1生物发酵过程的特征

生物发酵是属于强耦合、多变量、强烈时变性、高度非线性过程，是一个极为复杂的生化反应.由于目前基于发酵动力学以及生化反应工程的研究有限，且建立机理模型的理论建模方法尚不成熟，导致一些方法难以应用到实际中.现有部分通过实验经验得到的控制模型，以及某些凭借经验假设出的机理模型，因为这些模型适用范围存在一定的局限性，所以很难对非线性系统进行准确有效地控制，因此，发酵过程控制模型的有效建立成为难题[3].

发酵过程往往涉及到众多物理过程和化学反应.因此，发酵过程具有与物理和化学过程迥然不同的特征：

(1) 发酵系统动力学机理模型呈高度的非线性；

(2) 由于发酵过程动力学机理模型的参数变化不定，且具有强烈的时变性，因此，某些生物过程无法用固定的数学模型来进行描述；

(3) 由于生物过程包括众多的物理和化学过程，因此，他们之间的相互作用必然影响到整个发酵过程的响应速率，导致在线测量数据带有大幅时间滞后的特征.

上述发酵过程的特性，使得传统控制中的线性动力学模型与优化理论难以符合控制要求[4-6].

1.2发酵过程的控制要素

发酵过程的控制最主要包括环境因素以及与生理特性相关的优化控制两个方面，具体如下：

(1) 环境因素的控制：主要是PH值、温度、通风量等参数的控制，发酵过程能否正常进行的先决条件在于这些参数是否稳定，因为任何菌体的生存对环境的温度、含氧量、酸碱度等条件都有一定的要求.

(2) 生理特性相关的优化控制：是指产物的形成、传递过程、培养基添加等方面的控制.生理特性中的传递过程控制主要是溶液中含氧量的控制，因为在发酵过程中氧气是微生物生长、产物合成的必需条件，尤其是高产发酵生产中，含氧量的控制显得尤为突出.含氧量的控制制约因素主要由搅拌转速和空气流量两部分组成，其中搅拌转速的影响比空气流量的影响更为重要.

1.3发酵过程中的状态变量、可测量变量及操作变量

(1) 发酵过程的状态变量：一般如代谢产物浓度、基质浓度、菌体浓度、细胞的比增殖速率、CO2生成速率等，是指表征过程状态的参数，例如生物浓度、生物活性以及反应速率等.

(2) 测量变量：一般包括直接测量变量(一级)和间接测量变量(二级).发酵过程中典型的直接测量变量有发酵罐进出口处的气体分压、pH值、DO、电导率、黏度、菌体浓度、基质浓度、代谢产物浓度等.间接测量变量则有CO2生成速率、O2被摄取速率等，是指那些可以测量的状态变量，一般利用直接测量变量按照一定公式计算可以得到[7-8].

(3) 过程的操作变量：一般包括稀释率、搅拌速率、通气量、温度、压力、pH值等.通常是指所谓的环境因子或操作条件，改变这些条件可以导致发酵过程状态变量的变化，在某些情况下状态变量可以当成操作变量.

1.4发酵过程动力学模型

通常情况下，假定供料无菌且混合均匀，其中稀释速率D和供料基质浓度St可作为操作变量；出口的细胞浓度或生物浓度X、基质浓度S以及产品浓度P是过程的状态变量.多年来，许多学者用各种方法建立了许多模型来描述发酵过程，Henson和Seborg等1991年建立的发酵动力学模型是在众多模型中被广泛接受的动力学模型之一[9-11]，其模型为

(1)

式中μ是比生长率；Yn是细胞体产量；α和β是产品收益参数.为了简化，假设Yn、α和β均与操作条件无关.

式(1)中只提供了部分机理模型.比生长率μ包含过程的动力学特性，μ是发酵过程中的物理、化学、生物变量的复杂函数.有对μ动态特性模型进行大量描述，但由于对于特定发酵过程，且部分发酵过程更是找不到精确的表达式，所以，导致没有直接的模型可供选择.μ为不可测量的未知参数，设μ是状态变量函数，μ的值可通过可测量的状态变量的参数来估计.仿真中“真实”过程利用经典的haldane模型代表：

(2)

其中μm是最大比生长率；Pm是产品饱和常数；Km是基质饱和常数；Ki是基质抑制常数.

这个连续发酵过程的控制目标是单位时间内生成产品细胞的数量.实际生产中，发酵罐出口物料中，酵母细胞量与基质含量和产品浓度相比可以忽略，故控制目标可表示为：

Q=DP

(3)

2神经网络DMC控制算法

基于神经网络DMC控制模型的结构见图1.

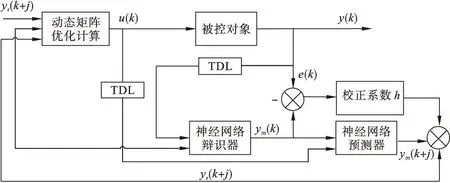
图1　神经网络预测控制结构

神经网络预测误差的能力体现在神经网络可描述非线性系统在预测模型中未能包含的一切不确定性信息，可以归结于利用一系列过去的误差信息来预测未来的误差，这不仅可以提高模型精度，还可以降低建立数学模型的负担.

下面是基于BP神经网络的动态矩阵预测控制的最优控制律的导出过程，其中优化计算是以神经网络预测模型为基础的.要获得最优控制律，必须使性能指标函数J趋于最小.

(4)

Δu(k)=dT[yr(k+1)-

y0(k+1)-he(k)]

(5)

式中：yr(k+1)为给定的参考信号；y0(k+1)为第k时刻预测无Δu(k)作用时未来N个时刻的初始矢量；e(k)为预测误差且 e(k)=y(k)-ym(k)；h为计算步长.

由于yr(k+1)是已知的输入信号，预测误差 e(k)在用神经网络对被控对象进行模型辨识得到ym(k)后求得，因此，要求出控制增量Δu(k)，关键是要求出y0(k+1)，而 y0(k+1)是由k时刻以前加在系统输入端的控制增量产生的，即在预测k时刻以后的控制增量为零，可以利用神经网络多步预测方法得到，由于y0(k+1)是由神经网络多步预测得到的，所以记为 ym0(k+1).

ym0(k+j)=g{Wg[VX0(k+j-1)]}

(6)

式中：j=1，2，…，p；

X0(k+j-1)=[ym(k+j-1),…,

ym(k+j-n),u(k+j-d),…,

u(k+j-d-m)].

u(k+j-d-i)=

“我们不是一个人在战斗！”省林科院副研究员陈景震幽默地说。他定点服务的是宜章县白石渡镇。那里，已经建起近两千亩板栗林，陈景震此行的目的是针对板栗林产量下降和落果的问题进行诊断，通过改良和科学种植，届时，板栗林的亩产有望从目前的60公斤提高到200公斤。

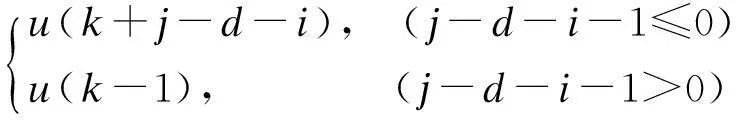
(7)

将式(6)与式(7)代入式(5)，则有：

Δu(k)=dT[yr(k+1)-

ym0(k+1)-he(k)]

(8)

根据动态矩阵预测控制的滚动优化方法，则基于BP神经网络的动态矩阵预测控制律为：

Δu(k)=[1,0,…,0]Δu(k)=

DT[yr(k+1)-ym0(k+1)-he(k)]

(9)

u(k)=u(k-1)+Δu(k)

式中DT=[1,0,…,0](ATQA+R)-1ATQ，将对象进行模型辨识后，在神经网络的输入端加入单位阶跃信号，根据网络的输出来求取A,进而求解DT，DT在控制运行时是不变的，所以可以先离线计算存入计算机内存即可.

在动态矩阵控制的基础上，针对谷氨酸发酵过程的误差，文中引入神经网络误差补偿预测控制方法，预测模型中未能包含的一切不确定性信息，可以归结为用BP神经网络用过去的误差信息预测未来的误差.它作为模型预测的重要补充，不仅可以降低建立数学模型的负担，而且还可以弥补对象模型中已简化或无法加以考虑的一切其他因素.

3谷氨酸发酵过程仿真

3.1神经网络动态矩阵控制的仿真

在BP神经网络建模过程中，采用同样本训练数据.在仿真中，进料基质浓度S作为操作变量，最大比生长率常数μm=0.5 h-1，基质消耗率Yn=0.4 g/g，模型常数km=1.2 g/L和ki=22 g/L.

模型输出采用式(2)，参数μ的表达式假设是简单的Monod模型.

(10)

取初值X=0.5 g/L，S=0.5 g/L，P=14.87 g/L，进料基质浓度取定值，即S=6 g/L.仿真结果如图2、图3所示.

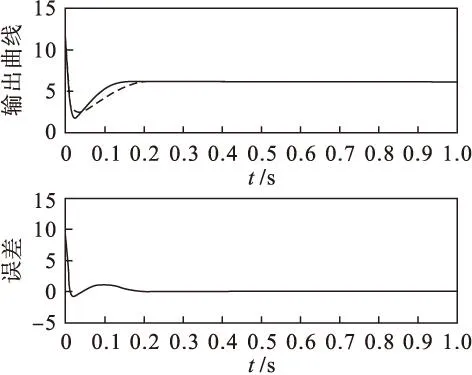
虚线—模型输出　实线—系统输出

检测发酵过程中菌体生长状态至关重要，它将决定整个发酵的产酸水平情况.通过分析谷氨酸发酵过程的工艺过程，选择影响菌体浓度的可测量参数，建立混合式的模型，通过仿真证明该方法具有较高的精度，收敛速度快，泛化能力强.只要使训练数据覆盖面广，设置好智能算法的各项参数，其预测精度将会进一步提高.

3.2基于误差补偿的神经网络动态矩阵控制的仿真

采用3.1节同样的模型和参数，通过仿真与其进行比较，证明基于误差补偿的神经网络动态矩阵控制的优越性.仿真结果见图4.

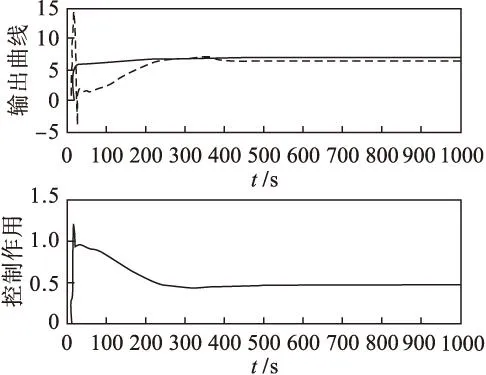
虚线—模型输出　实线—系统输出

通过仿真证明该方法具有更高的精度，收敛速度快，泛化能力强.此模型可以应用于实际的谷氨酸生产过程，因为训练数据来源于实际生产过程，只要将模型编程实现到现场的计算机控制系统中即可，由此得到菌体浓度和基质浓度的测量估计.

3.3多入多出谷氨酸发酵系统仿真

有时根据工业需要，谷氨酸发酵系统可增加多个输入和输出，例如，增加一个输入量供料基质浓度和一个输出量菌体浓度.模型参数：供料基质浓度设定值5 g/L和菌体浓度10 g/L，其余参数同3.1节.仿真结果见图5～图8.

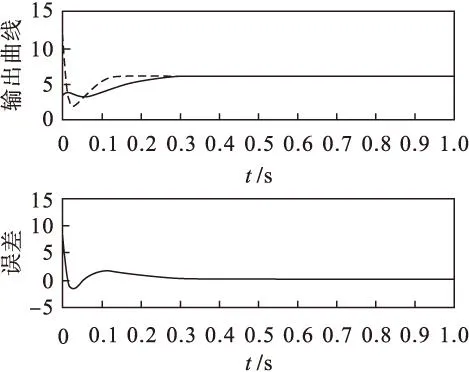
虚线—模型输出　实线—系统输出

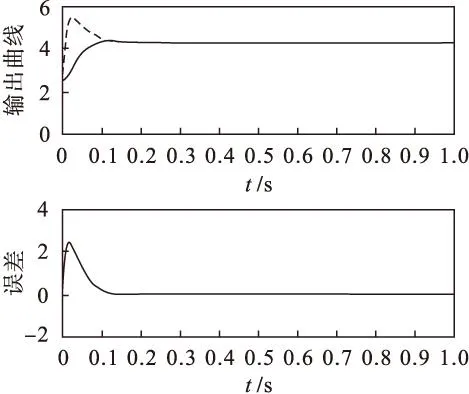
虚线—模型输出　实线—系统输出

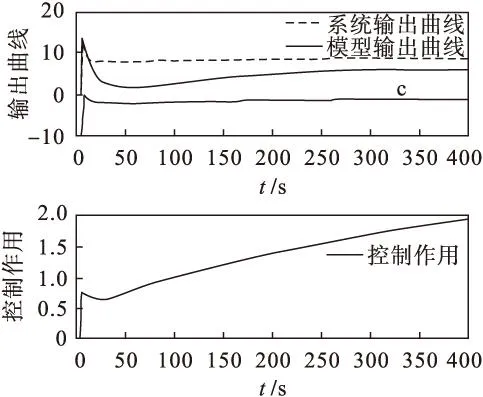
实线—模型输出　虚线—系统输出

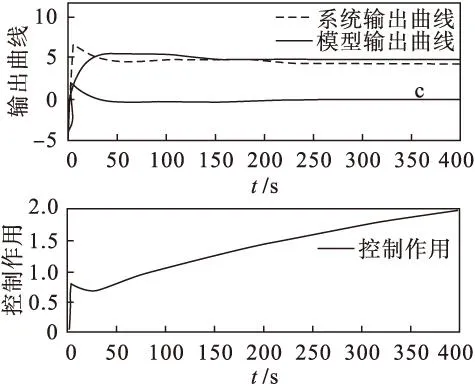
实线—模型输出　虚线—系统输出

通过仿真证明该方法对多入多出非线性系统也具有较高的精度，快速的收敛性，泛化能力强.此模型可以应用于实际的谷氨酸生产过程，因为训练数据来源于实际生产过程，只要将模型编程实现到现场的计算机控制系统中即可，由此得到菌体浓度和基质浓度的测量估计.

4结论

文中针对谷氨酸发酵过程具有的非线性、常规算法难于获得好的控制效果的状况，研究了神经网络预测控制以及基于误差补偿的神经网络预测控制，通过仿真结果表明：该方法可以实现对谷氨酸发酵过程多种模型的有效控制.

参考文献：

[1]朱新鹏.谷氨酸发酵生产的过程控制 [J].农产品加工，2011(5)：65-67.

[2]薛福珍，庞国仲，胡京华，等.啤酒发酵温度的多变量控制[J].自动化学报，2002， 28(1):150-154.

[3]吕伟珍,虎恩典,谢楠,等.Matlab仿真在谷氨酸发酵过程中的应用[J].自动化仪表，2012，33(5):57-59.

[4]GADEN E L Jr.Fermentation Process Kinetics[J].Biotechnology and Bioengineering,2000,67(6):629-634.

[5]AYNSLEY M,HOFLAND A G,MONTAGUE G A,et al.A Bioprocess Supervision Control and Analysis Integration System[C].San Diego:Proceedings of the American Control Conference,1990： 1992-1998.

[6]YANG G H，WANG J L，SOH Y C.Rcliablc Slalc Feedback Control Synthcsis for Uneertain Lincar Systems[J].Asian Journal of Control,2003，5(2)：301-308.

[7]刘森芝.谷氨酸发酵生产菌的研究与开发[J].发酵科技通讯，2009，38(2)：30-31.

[8]李人厚.智能控制理论和方法[M].2版.西安：西安电子科技大学出版社，2013： 75-98.

[9]邹健.智能预测控制及其应用研究[D].杭州：浙江大学，2002：3-5.

[10]许超,陈治纲，邵惠鹤，等.预测控制技术及应用发展综述[J].化工自动化及仪表,2002,29(3)：1-3.

[11]席裕庚,李德伟,林姝.模型预测控制：现状与挑战 [J].自动化学报，2013，39(3):222-236.

dynamic matrix control

Model Predictive Control Based on Error Compensation for Glutamic Acid Fermentation Process

GUAN Chang-liang,WANG Gui-cheng

(Shenyang University of Chemical Technology, Shenyang 110142, China)

Abstract:Glutamic acid fermentation process is biochemical process with high nonlinearity,strong time-varying and large lag,its internal mechanism is very complex.Nonlinearity exists in most of real subjects for fermentation process industryAnd the nonlinearity characters do not allow for linear approximation.Since some features of high nonlinear system cannot be instead of linear equation approximately,it must adopt nonlinear analysis technology.The paper combines both neural network and pre dictive control,which is to solve the problem of nonlinear control.Firstly,it realizes the predictive ability of nonlinear model by neural network.Then,it brings in dynamic matrix control to establish the prediction system of neural network based on error compensation glutamic acid.The multistep prediction is carried out by rolling optimization,feedback compensation and error compensation.Finally,it is constructed the multivariable nonlinear control system for glutamic acid fermentation.Simulation results show that the method can realize the valid control for for the nonlinear process of glutamic acid fermentation.

Key words:glutamic acid fermentation process;nonlinear system;neural network;multivariable;

中图分类号：TP23

文献标识码：A

doi:10.3969/j.issn.2095-2198.2016.01.014

文章编号：2095-2198(2016)01-0070-06

作者简介：关长亮(1988-)，男(满族)，辽宁丹东人，硕士研究生在读，研究生国家奖学金获得者，主要从事复杂过程建模的研究.通讯联系人：王贵成(1972-)，男，辽宁抚顺人，副教授，博士，主要从事计算机控制系统、工业过程模型化与控制的研究.

基金项目：国家自然科学基金资助项目(61104093)

收稿日期：2014-03-16