铁路枢纽内沪杭高铁列车开行站调整对不同特征旅客吸引的影响
张 戎, 诸立超
(同济大学 交通运输工程学院 道路与交通工程教育部重点实验室, 上海 201804)
为促进城市经济发展和规模扩张、缩短高铁线路长度、保证转弯半径,我国大部分高铁车站建于城市郊区或新城,该布局导致高铁旅客市内交通不便,增加高铁旅客“门到门”出行时间和费用。以沪杭客运通道为例,主要有高铁(简称“G”)、动车(简称“D”)、普通铁路旅客列车(除高铁和动车外的其他铁路旅客列车,简称“P”或普客)和大巴(简称“B”)4种地面公共交通方式,上海开行沪杭高铁和动车列车的车站位于外环线以外的铁路虹桥站(简称“虹桥站”),铁路上海南站(简称“上海南站”)仅开行两地间普客列车,上海长途汽车客运总站(简称“汽车总站”)开行两地间大巴,其中上海南站和汽车总站均位于中心城区。根据上海铁路局和上海汽车总站提供的数据,2013年沪杭客运通道4种城际出行方式的分担率分别为44.291%、16.097%、36.275%和3.338%,虽然高铁列车在城际间的平均旅行速度与普客列车和大巴相比优势较大,但由于虹桥站远离市中心使高铁旅客市内交通出行不便,削弱对旅客的吸引力,若适当调整高铁列车开行站将有助于提升其分担率。因此要调整高铁列车开行站以改善市内交通,关键在于掌握旅客在不同服务水平下的出行方式选择行为,借助离散选择模型可有效解释市内交通服务水平对城际出行方式选择的影响。
目前应用离散选择模型研究城际出行行为的成果较为丰富,采用的模型主要有多项logit(multinomial logit,MNL)模型[1-9]、巢式logit(nested logit,NL)模型[2]、排序logit(ordered logit,OL)模型[7]和混合logit(mixed logit,ML)模型[9]等,研究重点为未来年分担率划分[1-6]、开行方案评价[5,7]、出行选择行为分析[5,8]和分段时间价值测算[3,9]等,并解决城际出行方式选择研究领域的RP/SP(revealed preference,行为偏好;stated preference,意向偏好)数据融合[2]和低频率出行方式抽样数据偏差[8]等实际问题。但目前仅有少量文献将市内交通时间和费用纳入城际出行方式选择研究范围[1-3,6,8-9],考虑到旅客心理态度和感知、时间及费用等方面在市内交通、候车和在车(指旅客在高铁和动车等列车上站到站的过程,其对应时间称为在车时间)等分段过程中存在的差异,其中一部分研究为分段过程时间设定不同的待估参数以研究不同段时间价值的差异[2-3,8-9],文献[3]和[9]均得到候车时间价值最高的结论;此外,大部分研究侧重于旅客偏好揭示、需求分析和方式划分,主流处理方式是将不同城际出行方式时间设定为同一待估参数[1-3,7-8],不仅减少模型参数数量、方便模型结果分析,也有利于提高模型参数估计精度;少部分研究以测算不同城际出行方式时间价值差异为主要研究目的[4],将不同城际出行方式时间设定为不同待估参数,但对样本数量和精度要求较高,伴随着参数数量的增加,极有可能得到不显著甚至违反直觉的参数估计值。因此该方法的应用更为局限。而研究旅客特征所引起的城际出行选择行为异质性的文献则更少[3,8-9],并且尚未从调整高铁列车开行站角度研究如何提升高铁分担率。考虑到我国高铁车站布局带来的市内交通衔接问题及对高铁短途客流吸引的影响,本文以沪杭城际出行链旅客为研究对象,其中城际出行链包括起点城市市内交通、步行、候车、在车和目的地城市市内交通,通过纳入市内交通和旅客特征以避免分担率有偏估计问题,同时提升模型对旅客选择行为的解释能力和分担率预测精度;并借助NL模型量化不同特征旅客子群体面对市内交通改善表现出的选择行为异质性,提高模型精度;比较沪杭高铁列车由虹桥站开行和由上海南站开行两个不同方案下的高铁分担率,为未来沪杭高铁列车开行站的调整提供依据。
1 数据分析
1.1 数据采集
根据实地调研和文献阅读,本文选取市内交通时间(涵盖沪杭两地市内交通时间)、候车时间(涵盖火车站/汽车站内步行时间和候车时间)、在车时间和出行链费用(涵盖沪杭城际“门到门”出行费用)为城际出行方式选择主要影响因素,同时考虑旅客特征,通过对出行链服务属性水平根据现实范围边界进行合理波动以得到SP场景[10]。课题组于2014-03-28开展试调查,根据旅客反馈改善问卷和调查形式,并于2014-04-01~2014-04-05进行正式调查。调查地点为虹桥站、上海南站和汽车总站候车室及车厢,通过随机抽样调查最终回收309份沪杭方向有效问卷,调查内容包括:旅客特征如年龄、收入、出行目的和同行人数等,市内交通情况如时间和费用等,属性感知如可接受市内交通时间和步行时间等,以及用于揭示旅客在不同出行链服务水平下选择机理的4个SP场景。
1.2 统计分析
1.2.1 旅客特征
根据表1对样本数据的统计可知,本次受访者的年龄和收入跨度较大,基本覆盖沪杭城际旅客所有样本。进一步按高铁、动车、普客和大巴等4个细分市场分析旅客特征及市内交通属性,并计算表征细分市场旅客特征均值与整体市场旅客特征均值差异的平均绝对百分比误差MAPE为
( 1 )
式中:s为第s个旅客特征;t为第t种沪杭城市出行方式,共T种;As为第s个旅客特征的整体市场均值;Fts为第s个旅客特征第t种沪杭城市出行方式的细分市场均值。
由表1可知:
(1) 4个细分市场在性别、收入、报销和同行人数方面存在较大差异,说明有可能影响旅客城际出行方式选择,下文的参数估计证实性别和收入对选择行为影响显著,而报销和同行人数并不起重要作用;
(2) 4个细分市场在年龄、大包、小包、行李数和同行人数等方面并无显著差异,可预见其对沪杭城际出行方式选择并无显著影响,下文也印证该点;
(3) 旅客收入越高,越倾向于选择高铁,然后依次为动车、普客和大巴;
(4) 一般而言,男性旅客收入更高,样本均值为7 079元/月,而女性旅客收入较低,样本均值为5 763 元/月,具体表现为女性更倾向于选择动车,其次是普客,高铁为第3选择;
(5) 虹桥站远离市区,因此高铁和动车旅客市内交通时间均值较长,均为53 min,与普客和大巴旅客市内交通时间均值相比,分别长10 min和15 min;
(6) 高铁旅客市内交通费用均值为最高的19元,其次是普客和动车,分别为16元和15元,最低的大巴仅为6元。

表1 按城际出行方式分类的旅客特征及上海市内交通属性
注:女=1,男=0(对应变量为性别);有=1,无=0(对应变量为大包和小包);是=1,否=0(对应变量为报销);收入分为6个区间,第6区间为20 000 元/月及以上,前5个区间以均值表示,第6区间以20 000 元/月表示。
1.2.2 城际交通特征
由表2可知沪杭客运通道4种城际出行方式中高铁时间最短、费用最高,普客时间最长、费用最低,而大巴时间略短于普客,但费用逼近高铁,因此其分担率最低仅为3.338%,沪杭城际旅客收入较高,见表1,使其对时间的偏好甚于费用,因此选择高铁的旅客人数最多,高达44.291%。

表2 沪杭城际旅客城际交通属性真实值
1.2.3 市内交通特征
沪杭城际旅客在上海市内选择步行较少,不再考虑,可接受市内交通时间集中于16~30 min、31~45 min和46~60 min,见表3,均值为39.59 min,而实际市内交通时间均值为45.45 min,尚未达到旅客要求,主要因虹桥站远离市中心造成。

表3 沪杭城际旅客可接受市内交通时间
根据图1可知,通过核密度估计得到的市内交通时间概率密度函数形似对数正态分布:当市内交通时间较短时,由于城际旅客认为对市内交通具有较强的掌控和预测能力,易持乐观态度而低估市内交通时间;而市内交通时间较长时,城际旅客认为对市内交通的掌控能力较差,同时长距离出行时间不确定性更强,旅客易持悲观态度而高估市内交通时间;真实市内交通时间(均值45.45 min,标准差25.93 min)与预期(均值46.63 min,标准差27.38 min)相比更小。

此外,过长的市内交通时间将进一步增加旅客在高铁车站的候车时间,上海至南京的高铁旅客在铁路上海站(简称“上海站”)的候车时间,平均比上海至杭州的高铁旅客在虹桥站的候车时间少约7 min[11],其中上海站位于中心城区,而虹桥站位于外环线外,考虑到目前上海南站不开行沪杭高铁和动车列车,若沪杭高铁和动车列车开行由虹桥站调整至上海南站,由此带来的候车时间缩短可参照该数据。
1.2.4 客流分布特征
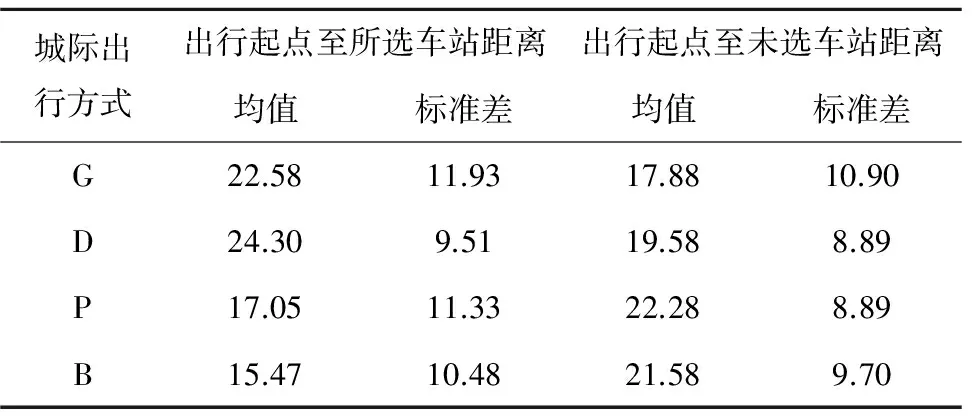
根据旅客填写的起点及所选车站信息,结合百度地图(http://map.baidu.com/)计算的路径距离,以旅客出行起点至所选铁路车站或长途汽车站的路径距离为横轴、以旅客出行起点至未选的最近铁路车站或汽车总站的距离为纵轴绘制二维图,见图2。以高铁旅客坐标(20,10)进行说明,20代表旅客至虹桥站的距离为20 km,10代表旅客至上海南站和汽车总站中较近车站的距离为10 km,即该点位于对角线右下方,说明旅客出行起点至所选车站的距离大于至未选最近车站的距离。由图2可知,高铁和动车旅客大部分位于对角线右下方,普客旅客分布相对均匀,总体上更接近上海南站,而大巴旅客分布集中于对角线周边,总体上距离汽车总站更近,说明虹桥站位置较偏,大量客流需经过长距离市内交通才能到达,而上海南站和汽车总站距离更近,见表4。市内交通出行距离的增加意味着市内交通时间不确定性增加,该不确定性使得旅客为不错过列车出发而增加候车时间,进一步导致城际出行链整体时间的增加。

表4 旅客至所选和最近未选车站的路径距离统计 km
2 城际出行方式选择模型构建及估计
2.1 模型简介
采用离散选择模型构建城际出行方式选择模型,离散选择模型通常根据决策者即旅客效用最大化假设推导得到,假定旅客n面临J种城际出行方式,并从第j种城际出行方式获得特定效用Unj,j=1,…,J,该效用被旅客感知到,但不能被研究者观测到,研究者只能观测到旅客面临的选择方案属性xnj∀j和旅客属性sn,通过函数Vnj=V(xnj,sn)∀j可将观测属性与旅客效用联系起来,称为代表性效用(Representative Utility),另一部分效用不能被研究者观测到,即Vnj≠Unj,效用被分解为Unj=Vnj+εnj,其中εnj捕捉到影响效用但并未包含在Vnj中的因素,称为不可观测项[12]。研究者不清楚εnj∀j,假设其联合密度函数为f(εn)。因此旅客n选择城际出行方式i的概率计算式为
Pni=ProbUni>Unj∀j≠i=
ProbVni+εni>Vnj+εnj∀j≠i=
( 2 )
式中:Pni为旅客n选择城际出行方式i的概率;Uni为代表性效用;εni为效用不可观测项;n为旅客;i、j为城际出行方式;I·为指示函数,括号内为真时I·=1,否则I·=0;fεn为εn的联合密度函数。
logit模型在不可观测项εni服从独立同分布的二重指数分布假设下推导得到,而probit模型则在εni服从多维正态分布的假设下推导得到,下文使用的是MNL模型和NL模型。
2.1.1MNL模型
由于εni独立同分布于二重指数分布,根据文献[12]推导得概率计算式
( 3 )
2.1.2NL模型
NL模型则在一定程度上克服MNL模型的IIA特性(independence from irrelevant alternative,不相关选择方案之间相互独立),概率计算式为
( 4 )
式中:λk为测度系数,用于度量巢k内城际出行方式效用不可观测项之间的独立程度,值越大独立程度越高,当λk=1时退化为MNL模型;Bk为巢,共K个,城际出行方式j被分配至K个不重复的巢B1,B2,…,BK中。
2.2 模型构建
考虑到本文的研究目的是分析沪杭城际旅客出行需求、探究市内交通改善对不同城际出行方式分担率的影响,故将不同城际出行方式的时间待估参数设定为相同;此外,考虑到调查地点主要为上海,旅客对杭州市内交通时间缺乏认知,为保证模型精度,仅考虑上海市内交通时间,据此构建包含服务水平和旅客特征变量,见表5的MNL模型和NL模型初始效用函数
Ung=θCCng+θTuTu,ng+θTwTw,ng+θTiTt,ng+
θRgRng+θBgBng+θHgHng+θQgQng+θMgMng+
θSgSng+θAgAng+θIgIng+Asc,g+εng
Und=θCCnd+θTuTu,nd+θTwTw,nd+θTiTt,nd+
θRdRnd+θBdBnd+θHdHnd+θQdQnd+
θMdMnd+θSdSnd+θAdAnd+θIdInd+Asc,d+εnd
Unp=θCCnp+θTuTu,np+θTwTw,np+θTiTt,np+
θRpRnp+θBpBnp+θHpHnp
+θQpQnp+θMpMnp+
θSpSnp+θApAnp+θIpInp+Asc,p+εnp
Unb=θCCnb+θTuTu,nb+θTwTw,nb+θTiTt,nb+εnb
( 5 )
式中:i=g,d,p分别代表高铁、动车和普客,b为大巴;θ为待估计参数;Asc为待估计常数项;其余变量见表5,参数预期正负中,正代表对应变量值越大效用越高,负代表对应变量值越大效用越低。

表5 模型变量及参数定义
2.3 参数估计结果
考虑到由于RP数据变量变化很小或共线性等造成的变量病态问题,采用SP数据对参数进行估计[12],由于SP数据为假设场景数据,得到的选择结果可能与真实选择有差异。因此本例基于RP数据构建SP数据以减小该差异带来的有偏估计。为得到精度更高和解释能力更强的模型,构建MNL模型和NL模型以供备选。根据2.2节所述的效用函数建立初始MNL模型,并按参数不显著程度逐步剔除变量,似然比指标未超过卡方分布临界值,说明剔除变量对模型并无显著影响,确定最终的MNL模型效用函数,见表6,进一步构建NL模型,见图3和表7,参数均借助NLOGIT软件采用牛顿拉普松算法进行估计。

表6 MNL模型变量筛选结果

由于沪杭客运通道4种城际出行方式不可观测效用项的方差未必完全相同,借助退化NL模型的包含值IV(inclusive value)估计,对确定NL模型的树形结构十分有帮助,从数据本身出发,不局限于出行方式和数据类型,才能最大限度地揭示选择枝之间的相关性。由图3左图可知普客和大巴的包含值与1无显著差异,故将普客和大巴放入名为“慢车”的巢中,而将高铁和动车视为退化枝方案,最终得到图3右图的树形结构。
表7中测度系数λ对应的t检验WT为
( 6 )
式中:λ为测度系数,即图3中数值,其中一个选择枝的λ必须被标准化为1;SD为测度系数标准差;WT为Wald检验值。
在表7测度系数λ的t检验3.14(-6.38)中,3.14是测度系数显著不等于0的t检验值,-6.38是测度系数显著不等于1的Wald检验值,两者绝对值均大于显著性水平为0.05时的临界值1.96,说明NL模型的测度系数显著不等于0和1,说明有必要构建NL模型[10]。剔除变量后的MNL模型和NL模型的最终效用函数为
Ung=θCCng+θTuTu,ng+θTwTw,ng+θTiTi,ng+
θSgSng+θIgIng+Asc,g+εng
Und=θCCnd+θTuTu,nd+θTwTw,nd+θTiTi,nd+
θSdSnd+θIdInd+Asc,d+εnd
Unp=θCCnp+θTuTu,np+θTwTw,np+θTiTi,np+
θSpSnp+θIpInp+Asc,C+εnp
Unb=θCCnb+θTuTu,nb+θTwTw,nb+θTiTi,nb+εnb
( 7 )
此外,旅客出行时间价值VOT可由边际替代率MRS估算,其定义为在整体效用保持不变前提下,旅客为缩短单位出行时间而多愿意支付的费用,两者参数比值即为旅客出行时间价值
VOT=MRStime-cost=
( 8 )
式中:VOT为时间价值;MRS为边际替代率;ΔUtime、ΔUcost分别为时间和费用变化所引起的效用变化值;dUtime、dUcost分别为效用对时间和费用的导数;∂U/∂T、∂U/∂C分别为效用对时间和费用的偏导;T可进一步划分为Tu、Tw、Ti,即θT可用θTu、θTw、θTi进行替换,用于测算不同段的时间价值;θT、θC分别为时间和费用的参数估计值。

表7 NL模型参数估计结果
注:t检验绝对值越大,则显著性水平p-value越小、参数估计越显著。
3 沪杭列车开行站调整对其竞争力的影响
考虑到高铁旅客以公务、探亲和旅游等目的为主,此类出行主要通往中心城区,同时短距离的城际出行旅客对市内交通时间更为敏感,因此有必要考虑虹桥站和上海南站在沪杭客运通道中的分工问题。对京沪长途出行旅客而言,假设旅客到达虹桥站的市内交通时间为45 min,目的地城市的市内交通时间同样为45 min,而京沪高铁旅客平均在车时间约5.6 h,可以接受1.5 h的市内交通时间;但对沪杭短途城际出行旅客,高铁城际交通时间仅约为1 h,1.5 h的市内交通服务水平恐怕难以令绝大部分旅客满意。因此可考虑将当前由虹桥站始发的大部分沪杭高铁和动车列车调整至由上海南站始发。该调整将使沪杭高铁旅客市内交通时间缩短近11 min,降至36.14 min,并使沪杭客运通道旅客市内交通时间均值由当前的45.45 min降至38.07 min,低于旅客平均可接受市内交通时间39.59 min的要求,同时使市内交通费用均值减少2.42 元/人次;进一步考虑到由此带来的候车时间缩短,结合调查数据和文献阅读[10]可知候车时间将缩短7 min,根据表7的时间价值可知市内交通改善所节约的广义成本(费用与时间成本之和)为10.86 元/人次。高铁开行站调整使得高铁城际出行的上海市内交通服务水平有所改善,并使市内交通时间、候车时间和市内交通费用有所下降,由此带来分担率的提升。

表8 沪杭高铁列车开行调整前后的城际出行方式分担率变化
由表7可知性别和收入对城际出行方式选择均有影响,并且优化高铁市内交通衔接将使其分担率有所提升,但对不同特征旅客子群体产生的影响不同,其中“↑”、“↓”分别代表某城际出行方式的分担率上升或下降,见表9,主要结果为:
(1) 旅客收入越高,对出行时间的要求更高,同时对出行费用的承受能力更强,因此高收入旅客更愿意转向费用更高、时间更短的高铁,而低收入旅客更多地选择费用较低、时间较长的动车;
(2) 高铁和动车分担率增量更多地来源于普客,说明较之于大巴,普客与高铁和动车存在更强的替代性;
(3) 当旅客收入为6 700 元/月时,其转向高铁和动车的分担率相同,均为3.080%;
(4) 一般而言,男性旅客收入更高,样本均值为7 079 元/月,高于临界值6 700 元/月,更容易接受费用更高的高铁,而女性旅客收入较低,样本均值为5 763 元/月,低于临界值6 700 元/月,故在高铁和动车开行站调整后,男性旅客更倾向于选择高铁,而女性旅客更倾向于选择动车。

表9 旅客子群体在高铁开行站调整前后的城际出行方式分担率变化 %
4 结论
本文以沪杭客运通道旅客为研究对象,通过问卷调查数据分析沪杭城际旅客特征、市内交通特征和客流分布特征,比较市内交通服务水平现状与旅客要求的差异;进一步将市内交通服务属性作为影响城际出行方式选择的城际运输链的一部分纳入进来,构建包含高铁、动车、普客和大巴等4种出行方式在内的城际出行方式选择模型,即MNL模型和NL模型;结果说明出行链费用、市内交通时间、候车时间、在车时间、性别和收入对城际出行方式选择影响显著。以较优的NL模型为基础,比较当前沪杭高铁和动车列车由虹桥站开行,以及未来沪杭高铁和动车列车由上海南站开行两个不同方案的沪杭高铁和动车分担率。继而结合旅客特征变量对不同子群体的选择行为进行比较,结果说明沪杭高铁和动车列车由上海南站开行的方案将吸引更多的高收入群体以及男性旅客选择沪杭高铁,而年龄、是否报销、行李数和同行人数等旅客特征对沪杭城际旅客的出行方式选择并无显著影响。但根据常数项显著可知,仍有一些影响城际出行方式选择的变量尚未纳入到模型中,未来有必要增加其他变量进一步揭示城际出行方式选择机理;此外,下一阶段需要研究沪杭高铁线接入上海南站的建设方案,并从调整后车站通过能力、枢纽区间通过能力、动车段高铁存车能力和养护维修作业能力等方面开展调整方案可行性研究。
参考文献:
[1] 何宇强, 毛保华, 陈团生, 等. 高速客运专线客流分担率模型及其应用研究[J]. 铁道学报, 2006, 28(3): 18-21.
HE Yuqiang, MAO Baohua, CHEN Tuansheng, et al. The Mode Share Model of the High-speed Passenger Railway Line and its Application[J]. Journal of the China Railway Society, 2006, 28(3): 18-21.
[2] 张戎, 吴晓磊, 张天然. 基于RP/SP融合数据的沪杭客运通道公铁客流分担率研究[J]. 铁道学报, 2008, 30(6): 7-13.
ZHANG Rong, WU Xiaolei, ZHANG Tianran. The Railway and Highway Mode Split Analysis in Huhang Corridor Based on RP/SP Combined Data[J]. Journal of the China Railway Society, 2008, 30(6): 7-13.
[3] 张戎, 吴晓磊. 长三角快速客运网城际公共交通分担率模型[J]. 同济大学学报(自然科学版), 2008, 36(9): 1 210-1 215.
ZHANG Rong, WU Xiaolei. Inter-urban Public Transport Mode Share under High-speed Railways Network in Yangtze River Delta[J]. Journal of Tongji University: Natural Science,2008,36(9):1 210-1 215.
[4] 朱顺应, 李军, 李安勋, 等. 城市群轨道交通方式划分非集计logit模型[J]. 武汉理工大学学报(交通科学与工程版), 2009, 32(6): 1 063-1 066.
ZHU Shunying, LI Jun, LI Anxun, et al. The Disaggregate Logit Model for Mode Split of Rapid Railway in the Urban Agglomeration[J]. Journal of Wuhan University of Technology:Transportation Science & Engineering, 2009, 32(6): 1 063-1 066.
[5] 叶玉玲, 王艺诗. 沪杭运输通道内旅客出行方式选择行为研究[J]. 铁道学报, 2010, 32(4): 13-17.
YE Yuling, WANG Yishi. Research on Travel Mode Choice Behavior in Shanghai—hangzhou Transport Corridor[J]. Journal of the China Railway Society, 2010, 32(4): 13-17.
[6] 彭辉, 续宗芳, 韩永启, 等. 城市群城际运输结构配置客流分担率模型[J]. 长安大学学报(自然科学版), 2012, 32(2): 91-95.
PENG Hui, XU Zongfang, HAN Yongqi et al. Sharing Ratios Model of Passenger Flows in Intercity Transportation Structure Configuration among Urban Agglomeration[J]. Journal of Chang’an University:Natural Science Edition, 2012, 32(2): 91-95.
[7] 王孝之, 赵胜川, 闫祯祯. 基于Rank Logit模型对城际交通分担率的计算方法研究[J]. 交通运输系统工程与信息, 2012, 12(2): 137-143.
WANG Xiaozhi, ZHAO Shengchuan, YAN Zhen-zhen. Intercity Transport Mode Spilt Calculation Method Based on Rank Logit Model[J]. Journal of Transportation Systems Engineering and Information Technology, 2012, 12(2): 137-143.
[8] 陈颖雪, 董治, 吴兵, 等. 基于选择方案抽样调查的城市群低频率出行行为研究[J]. 中国公路学报, 2013, 26(3): 158-163.
CHEN Yingxue, DONG Zhi, WU Bing, et al. Study on Low-frequency Intercity Travel Behavior of Urban Agglomeration Based on Choice-based Sampling Survey[J]. China Journal of Highway and Transport, 2013, 26(3): 158-163.
[9] ROMAN C, MARTIN J C, ESPINO R, et al. Valuation of Travel Time Savings for Intercity Travel: The Madrid-barcelona Corridor[J]. Transport Policy, 2014, 36(1): 105-117.
[10] HENSHER D A, ROSE J M, GREENE W H. Applied Choice Analysis: A Primer[M]. Cambridge: Cambridge University Press, 2005, 88-99.
[11] 孙小兴. 高速铁路与市内交通衔接的问题研究[D]. 上海: 同济大学, 2012:41-54.
[12] TRAIN K E. Discrete Choice Methods with Simulation[M]. Cambridge: Cambridge University Press, 2009, 11-33.
[13] KOPPELMAN F S, BHAT C. A Self Instructing Course in Mode Choice Modeling: Multinomial and Nested Logit Models[R]. Washington: US Department of Transportation Federal Transit Administration, 2006:157-174.

