丰厚表象累积夯实概念形成——《点到直线的距离》教学设计（二）

傅斌/汪杰

【教学内容】

人教版四年级上册第五单元第59页例3。

【教学思考】

从教材体系来看，点到直线的距离对后续学习“高”有着深刻的影响。如点到直线的距离定义为“从直线外一点到这条直线所画的垂直线段最短，它的长度叫做点到直线的距离”；平行四边形的高定义为“从平行四边形一条边上的一点向对边引一条垂线，这点和垂足之间的线段叫做平行四边形的高”。比较两者的概念定义，我们发现核心要素都是垂直线段，研究对象是点到对应的线；比较点到直线的距离与高的长度获得过程，我们发现两者都需要经历“找点——找对应线——作垂线——标垂足——量长度”的过程，操作步骤、技能要求几乎一致。

从教材内容来看，“点到直线的距离”由三部分组成。第一板块编排了画“过点A到直线的线段”，发现“垂直线段最短”的性质。第二板块学习“点到直线的距离”概念。第三板块应用概念测量两条直线间的距离，发现“平行线间距离处处相等”的性质。两个性质的发现都是围绕概念展开的，前者凸显的是概念的核心要素，后者是概念的操作应用。

因此本节课教学重点就是让学生借助多重操作感知“垂直线段”和长度测量，经历多重过程自我构建“距离”。

【课中探索】

一、操作验证，感知垂直线段最短

1.出示点A和直线m，讨论：从点A出发到直线m你能画出几条线段?端点在哪里？”

图1

让学生先画线段，再指一指所画线段的两个端点。之后用电脑演示画线段，选直线上的端点标上字母，形成图1。

小结：可以画无数条线段，起点都是点A,另一个端点在直线上。

2.观察讨论：你觉得线段AD有什么特殊的地方？

生：线段AD与直线m垂直。

组织学生动手在练习纸上验证垂直。教师介绍指出“从点A到垂足D形成的线段叫做垂直线段”。

3.判断讨论：哪条线段是直线BE的垂直线段？

图2

生：线段AD。

师：线段AD真的是垂直线段吗？我们来验证一下。

媒体演示用三角板验证，发现未重合，否定线段AD。

组织操作思考：你能画出从A点出发到直线BE的垂直线段吗？

学生动手在练习纸上画垂直线段，展示交流正确画法，做好垂足标记，标上字母F。

【设计意图：学生对于垂直的判断，往往利用肉眼观察做出直觉判断，这里设计线段AD是否垂直的辨析环节，再次点击垂直的本质“两条直线相交成直角”，让学生感悟运用工具的必要性。】

4.讨论：在图2的这些线段中，你认为哪条线段长度最短？

生：线段AF。

师：怎么证明？

生：量一量线段的长度。

组织学生测量线段长度，展示后得到“垂直线段AF长度”最短。

5.（回到图1）再次讨论：这么多线段中，还是垂直线段最短的吗？可以怎样验证？

引导学生用观察法和测量法（比较接近于垂直的线段，采用测量法）再次验证。小结得出：从一点出发到直线的所有线段中，垂直线段最短。

【设计意图：通过让学生经历“猜想——验证”的过程，依托具体可见的长度数据，归纳发现“垂直线段最短”的性质，有利于培养严谨的科学态度。】

二、夯实过程，经历概念形成

1.教师介绍指出：通过测量，我们知道垂直线段AF的长度是3cm。在数学中，我们就可以说点A到线段BE的距离是3cm。

2.操作测量，探究距离。

（媒体呈现斜方向的直线m和直线外点B、点C）

（1）讨论：“要想知道点 B、点C到直线m的距离各是多少，你打算怎么办？”

师生交流中明确操作步骤：①画垂直线段，②量出长度。

（2）学生独立完成探究后，反馈错例（错例一：垂直不标准；错例二：线段一端超过点B），用媒体记录测量距离的数据（4厘米、5厘米）。

（3）反馈讨论“4厘米指的是什么？”，得出“4厘米是点B到直线m的垂直线段的长度”可以简说为“4厘米是点B到直线m的距离”。

3.概括提炼，形成概念。

讨论“什么是点到直线的距离？”，引导学生用自己的语言描述、概括概念，最后形成板书。

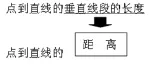
4.辨析比较，完善概念：点A到线段DE的距离是（ ）?

三、巩固应用，拓展概念外延

1.测量两直线间的距离。

（1）呈现一组平行线：组织学生任选3点，量出它们到另一条直线的距离。

（2）讨论：“通过测量，你发现了什么？”小结：平行线间距离处处相等。

（3）呈现一组相交的直线，组织学生任选3点，量出它们到另一条直线的距离。

观察讨论：你又发现了什么？

小结指出，相交的两条直线距离有大有小。

讨论：现在你怎样判断平行？

生：只要选几个点看距离是否相等，如果相等这两条直线平行。

2.从图形中找距离。

3.生活中应用距离：怎样测量跳远距离呢？

【设计意图：应用概念量距离，实现新旧知识的联结，帮助学生感悟验证平行从“想象无限延伸”到测量“距离是否相等”的理性判断；应用概念找距离，为知识的后续发展，正确地找“高”做准备；应用概念量跳远，实现生活与数学的对接，发展学生解决问题的能力。】

【总评】

一、多重操作助表象累积

“垂直线段”是“点到直线距离”概念的核心要素。为了让学生获得充分感知，建立清晰表象，教学中首先让学生“画线段”、“指端点”，唤起对线段的认知经验，强化了从“哪点出发”到“哪点结束”。其次让学生“验证垂直”、“画垂直线段”，激活判断垂直、画垂线的活动经验，强调了工具的运用，在操作中“两个端点”“垂直”的图像逐步清晰。在引出距离概念后，让学生独立作图探究距离，把此过程中出现的典型错例作为交流材料，在辨别“是否垂直”、“垂直线段与垂线”的过程中，帮助学生累积丰厚的表象，同时作图技能得到提升。

二、夯实过程促概念形成

在概念形成过程中，教师首先引出范例，让学生了解“距离”。其次采用师生合作、学生独立探究点B、点C分别到直线的距离,让学生在动手操作、交流辨析中理解“距离”。再次教师引导学生回顾操作过程，总结“什么是点到直线的距离”，从而提炼出“距离”。最后呈现辨析习题，围绕“是否垂直”“起点在哪”展开交流，让学生自我完善“距离”。整个过程中学生积极的运用旧知去“理解、修正、总结、反思”新知，在“平衡”与“不平衡”不断反复中建构的概念图式清晰，本质理解深刻。