拉剪复合试验测试炸药晶体/粘结剂界面力学特性

颜熹琳, 唐明峰, 甘海啸, 王 林, 李 明, 温茂萍

(中国工程物理研究院化工材料研究所, 四川 绵阳 621999)

1 引 言

高聚物粘结炸药(PBX)作为一类重要的高能炸药,广泛应用于武器战斗部中,在国防领域中具有重要地位。但是,PBX组分的特殊性(炸药晶体颗粒高度填充,且炸药晶体模量远高于粘结剂模量[1])和成型工艺的复杂性(由各组分经过造粒及高温高压压制而成)决定了PBX中界面大量存在,且结构异常复杂,界面处必然会出现热物理性能、力学性能等的跳跃。炸药晶体/粘结剂界面的力学特性研究对PBX的配方设计具有参考价值,对PBX力学性能的改善和安全性能的提高具有指导作用。

目前PBX界面力学性能的研究方法主要包括模拟计算[2-3]和试验测试[4-5]两种。南京理工大学的马秀芳等人[6]采用分子动力学方法计算PBX中奥克托今(HMX)/氟橡胶F2311的界面结合能为314.2 kJ·mol-1,且发现PBX中HMX与F2311之间存在氢键作用和较强的范德华力。Hackjin Kim等[7]采用和频振动光谱的方法测试了β-HMX单晶和高分子粘结剂Estane之间的界面情况,发现HMX的CH键延伸在HMX-Estane界面上比自由表面分裂更小,但作者同时指出该试验结果可能并不具有代表性。肖继军等人[8-9]通过分子动力学模拟方法理论研究了β-HMX晶体的(100)晶面与聚合物粘结剂聚乙二醇(PEG)、端羟基聚丁二烯(HTPB)和Estane5703之间的界面情况,包括界面结构、界面力学性能(例如界面的弹性性能和延展性等),研究发现,添加少量聚合物粘结剂,可以有效提高HMX晶体的延展性。Palmer等人[10]通过将HMX晶体与粘结剂粘接后开展直接拉伸试验,测量了EDC37(一种高聚物粘结炸药)中HMX与聚合物粘结剂之间的界面断裂所需要的力,发现该界面强度仅有75 kPa。这些研究为认识PBX中炸药晶体/粘结剂的界面力学特性提供了途径,但其中数值模拟等间接方法偏多,而针对PBX真实界面的力、变形等参量的直接测量则很缺乏。

基于此,本研究针对压装PBX的界面特性,设计了可实现拉剪复合加载的多角度拉伸夹具和PBX模拟界面的制备方法,开展了PBX模拟界面力学特性试验方法研究,对PBX模拟界面在不同加载角度下的力学行为特征进行了试验分析,并对PBX界面的强度相关性规律进行探索。

2 实验部分

2.1 设计原理

图1为PBX中界面结构示意图, 其中炸药晶体数量众多,方向各异,界面构成复杂(图1b),但对于一个特定的界面,其受力状况都可分解为平行于界面的横向作用(剪切)和垂直于界面的纵向作用(拉压),且多以拉剪或压剪复合的形式承受载荷(图1c)。因此,为了复现PBX中炸药晶体/粘结剂界面的真实力学作用,必须使试样在受载过程中同时受到拉伸(压缩)和剪切的作用。对于绝大多数PBX来讲,拉伸和压缩下材料的宏观力学响应是不一致的,拉伸强度小于压缩强度,即存在所谓的拉压不对称性; 就微观破坏形式而言,二者也是不一致的,拉伸载荷作用下PBX的破坏形式主要表现为炸药晶体和粘结的分离,即脱粘,而压缩载荷下材料的破坏形式还包括炸药晶体的断裂和破碎。可见从受力和变量最小化的角度,拉伸、剪切的耦合对PBX中炸药晶体/粘结剂界面的力学分析无疑是更有利的。因此本研究重点考虑PBX中界面的拉伸、剪切复合作用。

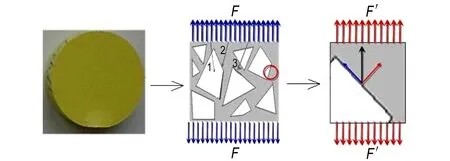
a. PBX sampleb. different crystal-binderc. load on

interface interface

图1PBX中炸药晶体/粘结剂界面示意图

Fig.1Schematic illustration of the crystal/binder interface for PBX

基于界面法向和载荷方向夹角可调、以实现正应力和剪应力的不同比例分配的设计原则,设计了一种界面测试装置,该装置可满足界面的拉伸、剪切及拉剪复合测试需求。设计的拉剪复合加载装置及其装配工装如图2。通过插销固定不同位置的定位孔,该装置可实现0°、15°、30°、45°、60°、75°及90°共7个不同角度的拉/剪加载试验。图3为粘结好的试样在0°、45°、90°三个角度加载时的实际效果图。根据受力分析,材料试验机横梁对夹具施加载荷作用时,界面上的拉伸载荷与剪切载荷分别为:

(1)

式中,F为横梁施加的载荷,Fn为界面上的拉伸力,Fτ为界面上的剪切力,单位均为N,α为试样轴向与载荷方向的夹角,°。

图2拉伸夹具实物图

1—弧形连接片, 2—试样粘结头, 3—试样安装夹具座

Fig.2Tensile fixture used in the experiment

1—arc connector, 2—bonding part, 3— samplefixture

a. tension(0°loading)b. 45°loadingc. shear(90°loading)

图3PBX界面力学特性测试工装示意图

Fig.3Tensile-shear fixture for crystal/binder interface test

2.2 材料及模拟界面的制备

研究对象为一种以TATB为基的高聚物粘结炸药,粘结剂为一种氟聚合物,采用压装工艺制备而成。为了从宏观加载的角度对PBX中炸药晶体/粘结剂界面进行力学性能分析,需要精确制备的界面。首先加工了Φ20 mm×20 mm的圆柱形试样,选取两发为一组,用手工和精密研磨抛光机对试样进行抛光,使炸药晶体从试样表面裸露出来,然后用粘结剂将两发试样抛光过的表面进行粘接形成模拟界面,最后在材料试验机上对模拟界面施加固定的压力(压力条件如图4所示),保压1 h,然后卸载压力后在常温下放置24 h,即制备了炸药晶体/粘结剂模拟界面。由于粘结剂在PBX含量极少,因此该模拟界面实际代表了PBX中炸药晶体/粘结剂界面的宏观统计效应,与PBX真实界面十分接近,可以替代真实界面进行力学性能研究。事实上,该PBX中超过90%的成分为TATB晶体,按组分密度简单计算可知模拟界面处炸药晶体-粘结剂占主要部分,而粘结剂-粘结剂间的接触面积小于5%,因此,从方法和规律上讲,通过该模拟界面得到的力学强度可以代表PBX中炸药晶体/粘结剂界面的相互作用。当然,更深入的理解应进一步分离其中晶体-粘结剂界面以及粘结剂-粘结剂界面的作用,此处又牵涉到炸药晶体的各向异性问题,这需进一步研究。

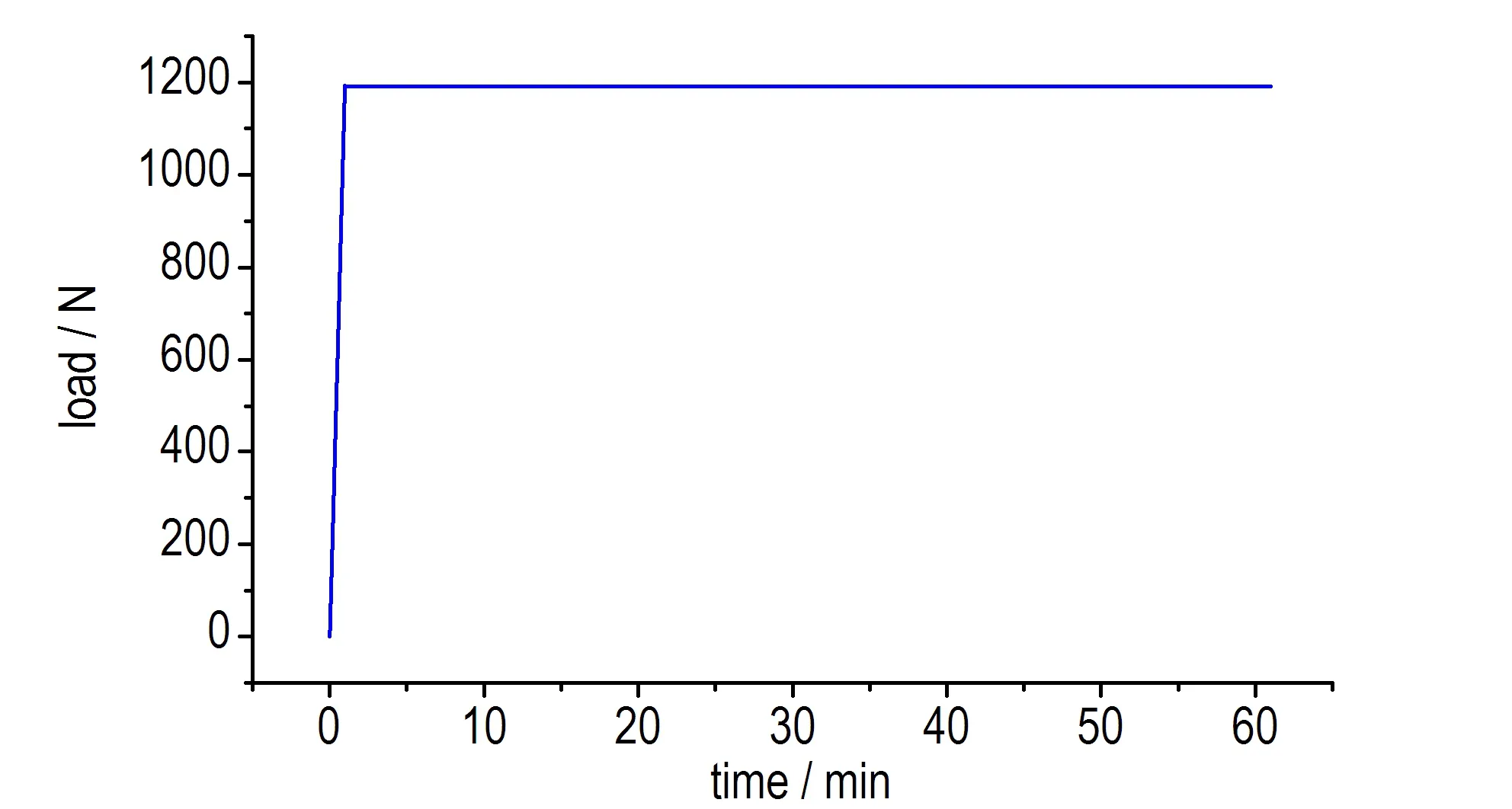
a. load-time curve

b. load-displacement curve

图4模拟界面制备压制曲线

Fig.4Compression curves of the simulated interface for PBX

2.3 界面的拉剪复合试验

通过上述设计的拉剪复合试验装置,对制备的模拟界面开展了0°、30°、45°、60°、75°、90°六个不同角度的界面力学作用测试试验(角度为试样和加载方向的夹角,并且定义0°为纯拉伸,90°为纯剪切)。试验温度23 ℃,加载速率0.5 mm·min-1。

3 结果与讨论

3.1 拉剪试验的有效性

图5给出了界面失效瞬间试样的破坏形貌,加载后试样从两块试样之间的粘结界面破坏,而两块小试样没有发生破坏,说明该试验的夹持加载确实满足了界面间的拉剪耦合测试。图6是不同加载角度下的载荷-位移曲线,其中每个加载角度5个试样,由图6可知每一个加载角度均具有较好的重复性。表1为不同加载角度的载荷平均值和标准差,可见随着加载角度的增加,试验结果稳定性良好。不同角度的拉剪复合试验结果的一致性表明了基于拉剪复合试验的炸药晶体/粘结剂界面作用力学特性测试方法的可行性。

图5试样的典型破坏形貌

Fig.5Typical failure model of the sample

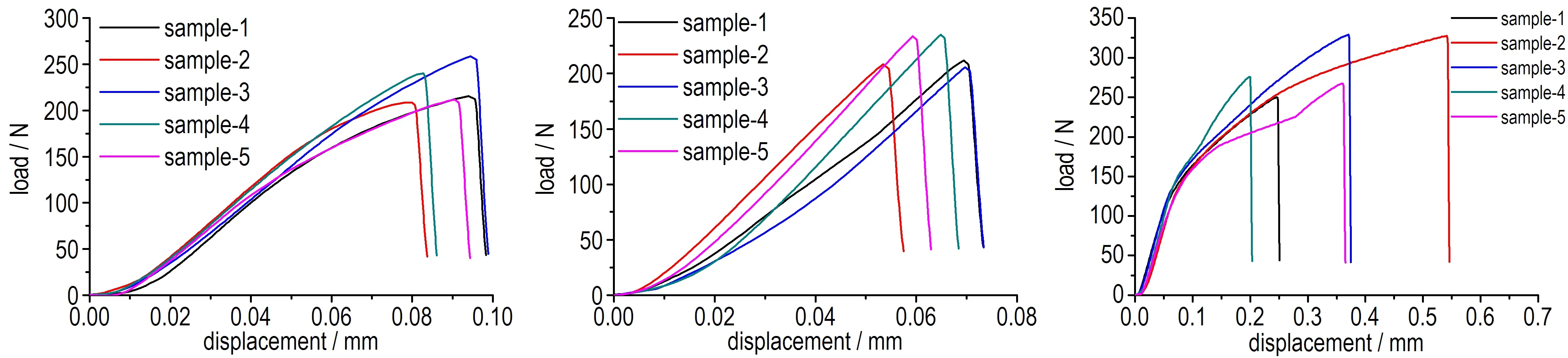
a. 0°b. 30°c. 45°

d. 60°e. 90°

图6不同角度拉剪复合试验结果

Fig.6Tensile-shear results in different loading angles

表1不同角度下的载荷平均值与标准差

Table1Average load and standard deviation in different loading angles

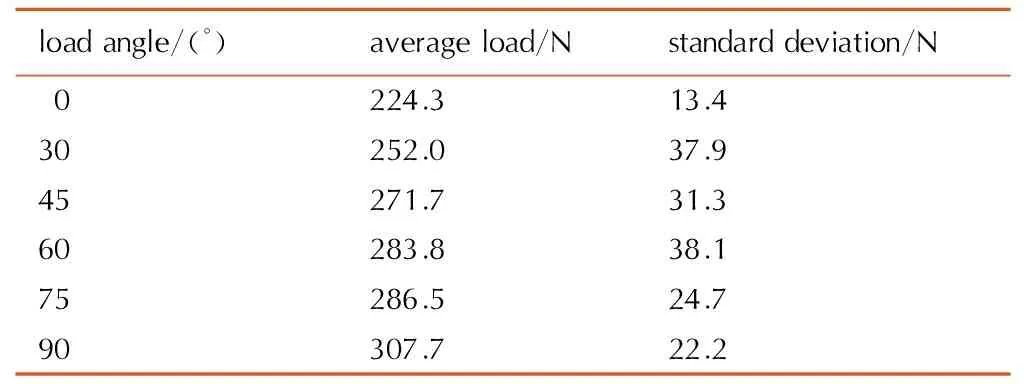
loadangle/(°)averageload/Nstandarddeviation/N0224.313.430252.037.945271.731.360283.838.175286.524.790307.722.2

3.2 PBX界面的力学行为特征

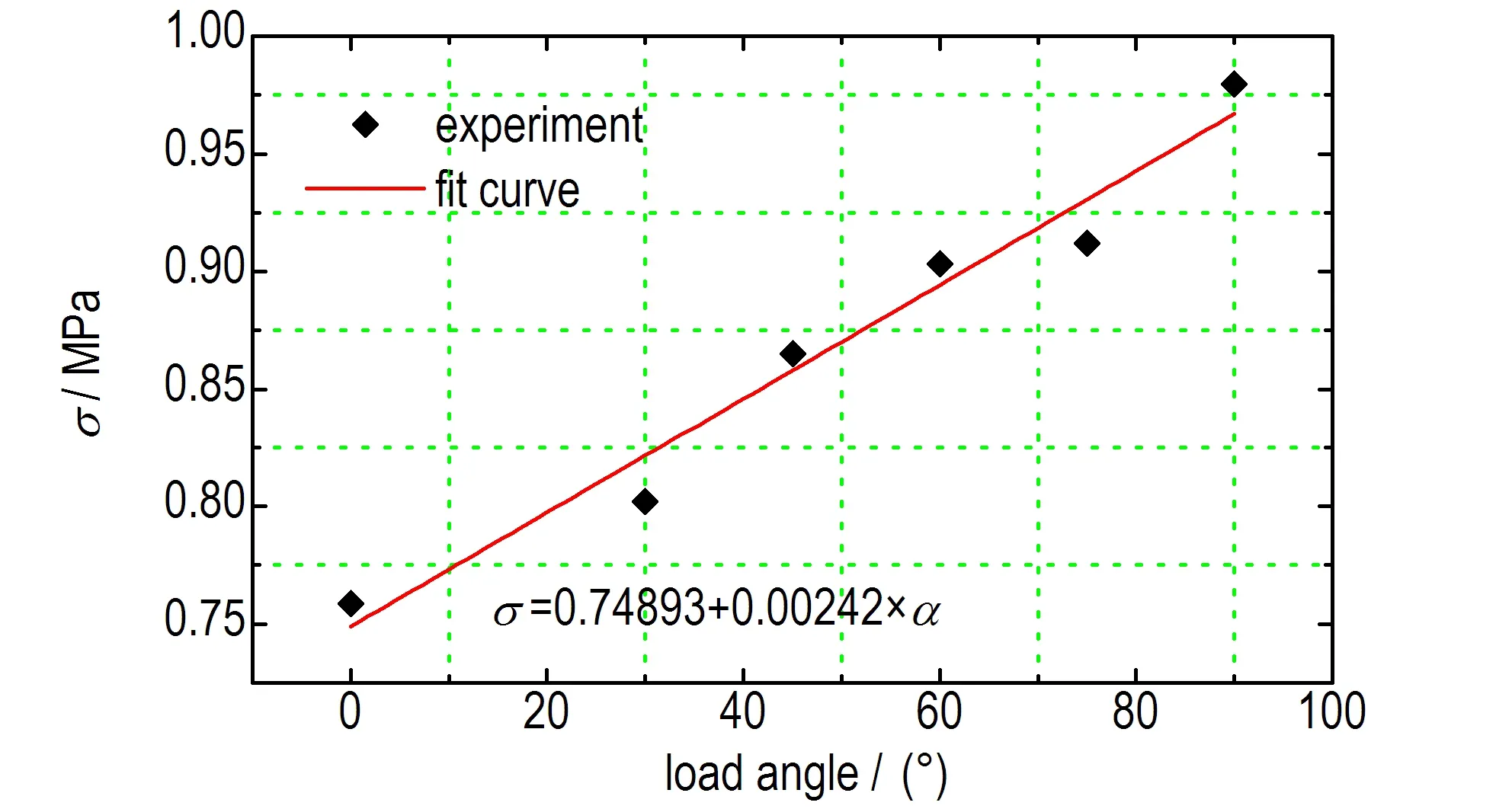
从不同角度的拉剪复合应力试验结果可以看出,模拟界面的失效载荷随着加载角度的增加而增加,而根据图6,模拟界面破坏对应的位移也几乎是随着加载角度的增加而增加的。初步分析认为,纯拉伸作用下,晶体和粘结剂的作用变化主要表现为晶体和粘结剂界面的脱粘,以及占很少比例的粘结剂断裂失效; 而纯剪切作用下,界面作用的变化还增加了晶体和粘结剂的摩擦作用。最终的结果是PBX界面的剪切破坏载荷大于拉伸破坏载荷,这与PBX宏观试验得到的剪切应力大于拉伸应力是一致的[11]。更深层次的原因还需进一步研究。

为便于分析,采取应力的形式,并把不同角度的拉剪复合应力分解到拉伸方向和剪切方向,得到对应角度的拉应力和剪应力,即把式(1)用应力进行表述:

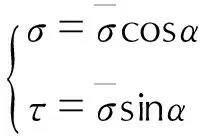
(2)

3.3 PBX界面作用模型

关于材料在拉剪、压剪复合应力共同作用下的强度相关性规律,研究者提出了各式各样的本构模型。对于混凝土、陶瓷等脆性材料,不论是基于试验数据分析,还是基于Drucker-Prager准则[12]或莫尔-库伦准则[12]的退化理论,均发现此类材料的拉剪、压剪强度相关关系可以用椭圆方程、抛物线方程、双曲线方程等二次曲线来表示[14-15]。本研究对象也是一种脆性材料,从3.2节炸药晶体/粘结剂界面作用规律来看,其破坏面上拉应力增加过程中剪应力是在减小的。在τ-σ平面上,一般认为材料的破坏条件由破裂面的正应力和剪应力共同决定,即

a. total stress

b. tensile and shear stress

图7拉剪复合应力随加载角度的变化

Fig.7Tensile-shear results in different loading angles

f(τ,σ)=0

(3)

式中，τ为剪切面上的剪应力,MPa;σ为剪切面上的拉应力,MPa。不同角度的界面拉应力和剪应力做成τ-σ平面上应力点,结果如图8所示。由图8可知,PBX模拟界面的拉剪强度规律近似为椭圆型,用式(4)对试验数据进行了拟合:

σ2/a2+τ2/b2=1

(4)

式中，a、b为材料常数,单位MPa。拟合结果如图8所示,图中a=0.759 MPa,b=0.970 MPa,可见拟合结果与试验数据吻合良好,表明式(4)代表的椭圆模型可以较好地反映PBX中炸药晶体/粘结剂界面的拉剪强度特性。

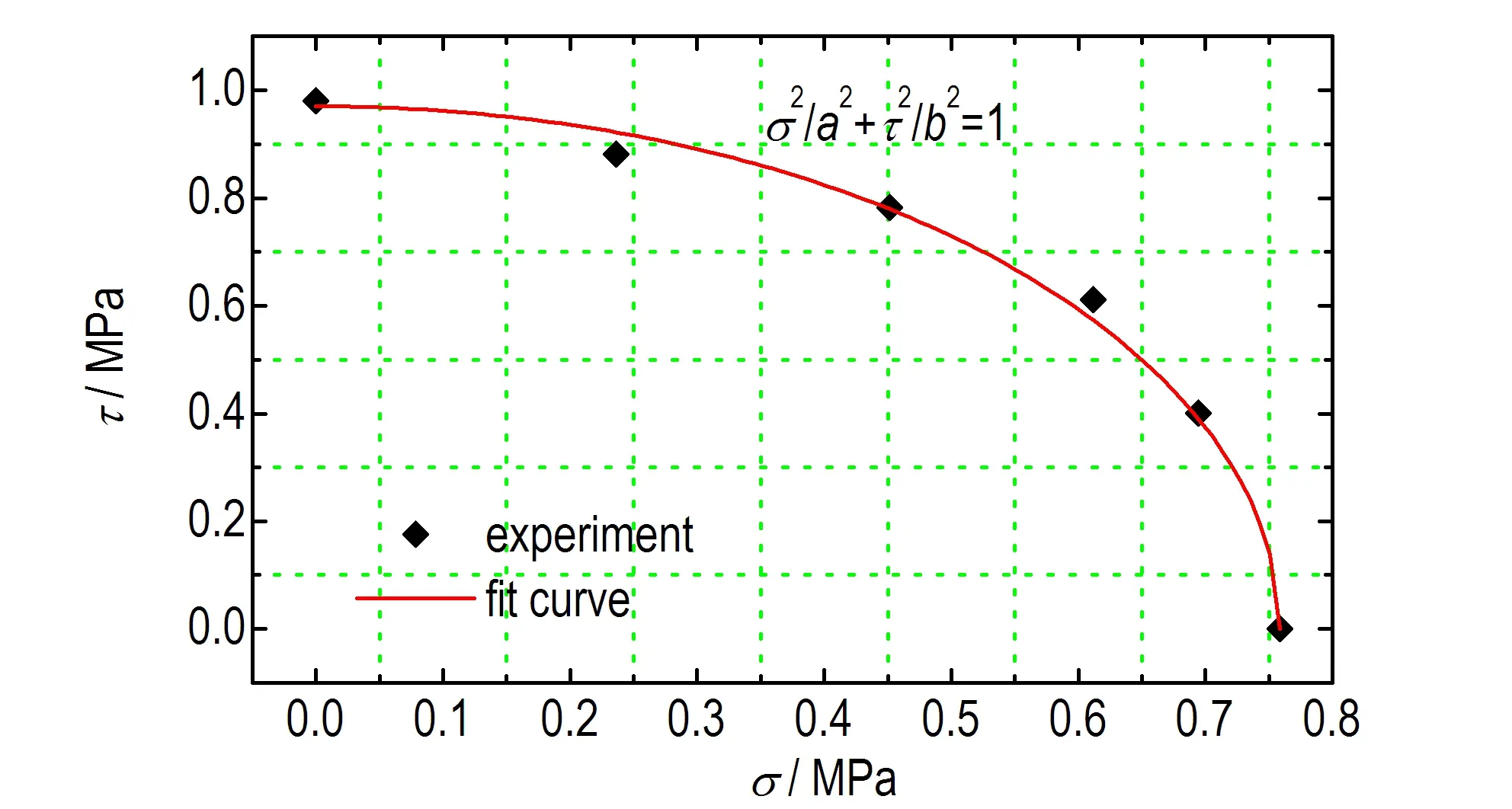
图8不同角度的界面拉应力τ和界面剪应力σ的试验结果以及拟合结果

Fig.8Experimental data and fitting curve of tensile-shear stress

4 结 论

(1) 设计了一种用于PBX界面拉剪复合加载的夹具,可实现0°、15°、30°、45°、60°、75°及90°的多角度加载,同时探索了PBX晶体/粘结剂模拟界面的制备方法,试验结果一致性较好,可用于PBX界面拉剪力学性能的相关研究。

(2) PBX界面的剪切破坏应力为0.980 MPa,大于拉伸破坏应力0.759 MPa,拉应力随着加载角度的增加不断降低,剪应力随着加载角度的增加不断增加,而复合应力随加载角度的增加线性增大,0°、30°、45°、60°、75°、90°加载角度下的应力分别为0.759,0.802,0.865,0.903,0.912 MPa和0.980 MPa。

(3) PBX界面的破坏准则由拉应力和剪应力共同控制,σ2/a2+τ2/b2=1形式的椭圆模型可以较好地描述PBX中炸药晶体/粘结剂界面的拉剪强度特性。

本研究涉及的试验方法适用于PBX中炸药晶体/粘结剂界面力学性能研究,特别是特定压力下成型的PBX界面的作用强度及破坏规律,结果可作为PBX配方研制过程中的借鉴。而对于PBX的成型过程,涉及到的因素还包括温度、保压时间等,实际应用中还可能受到冲击载荷的作用,后续的研究将进一步考虑这些因素的影响以及它们耦合作用下PBX界面的力学性能。

参考文献:

[1] 韦兴文, 李明, 李敬明, 等. 空隙对TATB基高聚物粘结炸药有效弹性模量的影响[J]. 含能材料, 2014, 22(4): 493-497.

WEI Xing-wen, LI Ming, LI Jing-ming, et al. Influence of pore properties on effective elastic modulus of TATB based polymer bonded explosive[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2014, 22(4): 493-497.

[2] Rae P J, Goldrein H T, Palmer S J P, et al. Quasi-static studies of the deformation and failure ofβ-HMX based polymer bonded explosives[J].ProceedingsoftheRoyalSocietyofLondon,SeriesA:Mathematical,PhysicalandEngineeringSciences, 2002, 458: 743-762.

[3] TAN H, HUANG Y, LIU C, et al. The Mori-Tanaka method for composite materials with nonlinear interface debonding[J].InternationalJournalofPlasticity, 2005, 21(10): 1890-1918.

[4] Haycraft J J. The elastic constants and related properties of the energetic material CL-20 determined by Brillouin scattering[J].TheJournalofChemicalPhysics, 2009, 131(21): 1-8.

[5] Drodge D R, Williamson D M, Palmer S J P, et al. The mechanical response of a PBX and binder: combining results across the strain-rate and frequency domains[J].JournalofPhysicsD:AppliedPhysics, 2010, 43(33): 335-403.

[6] MA X, ZHAO F, JI G, et al. Computational study of structure and performance of four constituents HMX-based composite material[J].JournalofMolecularStructure:Theochem, 2008, 851(1-3): 22-29.

[7] Kim H,Lagutchev A, Dlott, D D. Surface and interface spectroscopy of high explosives and binders: HMX and Estane[J].Propellants,Explosives,Pyrotechnics, 2006, 31(2):116-123.

[8] XIAO J J, HUANG H, LI J, et al. A molecular dynamics study of interface interactions and mechanical properties of HMX-based PBXs with PEG and HTPB[J].JournalofMolecularStructure:Theochem, 2008, 851(1-3): 242-248.

[9] XIAO J J, HUANG H, LI J, et al. Computation of interface interactions and mechanical properties of HMX-based PBX with Estane 5703 from atomic simulation[J].JournalofMaterialsScience, 2008, 43(17): 5685-5691.

[10] Palmer S, Williamson D, Proud W. Adhesion studies between HMX and EDC37 binder system[J].AIPConferenceProceedings, 2006, 845: 917-920.

[11] 董海山,周芬芬. 高能炸药及其相关物性[M]. 北京: 科学出版社, 1989.

[12] Hopkins H G, Prager W. The load carrying capacities of circular plates[J].JournalofMechanicsandPhysicsofSolids, 1954, 2: 1-13.

[13] Bai Y L, Wierzbicki T. Application of extended Mohr-coulomb criterion to ductile fracture[J].InternationalJournalofFracture, 2010,161(1): 1-20.

[14] Bresler B, Pister K S. Strength of concrete under combined stresses[J].JournalofACI, 1958, 55(3): 321-345.

[15] 蒋大骅. 国外混凝土强度理论研究述评[J]. 同济大学学报, 1978(1): 145-156.

JIANG Da-hua. A brief review on the failure criterion for concrete[J].JournalofTongjiUniversity,1978(1): 145-156.