1,1′-二羟基-5,5′-联四唑金属盐的制备及热分解动力学

王杰群, 王鹏程, 陆 明

(南京理工大学化工学院, 江苏 南京 210094)

1 引 言

调节推进剂的燃烧性能是固体推进剂研究的热点之一。为达到推进剂燃速调节范围宽和压强指数低的目的,一般采用添加燃烧催化剂的方法[1],而其中常用的惰性催化剂对推进剂能量损失较大[2],而含能催化剂因克服惰性催化剂的缺点得到了广泛关注和研究[3-4]。含能催化剂有很多种类,其中的唑类金属盐具有密度大、蒸气压低、极性强、热稳定性好、性能可调等特点,同时可降低推进剂的特征信号,有望成为推进剂的良好组分[4]。Li等[5]合成3,6-双(1-氢1,2,3,4-四唑-5-氨基)-1,2,4,5-四嗪(BTATz)铅盐,使双基推进剂(DB)推进剂在8～12 MPa范围内产生“麦撒效应”同时压强指数降至-0.065,使复合改性双基推进剂(CMDB)在4～12 MPa范围产生平台燃烧,同时压强指数降至0.18,是高效的含能催化剂[1]。

为使含能催化剂具有更多的候选物质,利用四唑化合物1,1′-二羟基-5,5′-联四唑(1,1′-BTO)[6]的酸性,通过复分解反应,合成了1,1′-二羟基-5,5′-联四唑的钴盐(1,1′-BTOCo)、铜盐(1,1′-BTOCu)和铅盐(1,1′-BTOPb)。通过DSC和TG研究三种盐的热分解行为,分别用Kissinger法[7]和Ozawa法[8-9]计算得到热分解表观活化能、指前因子、机理函数和动力学方程,进而计算其自加速分解温度(TSADT)、热爆炸临界温度(Tbpo)和热力学参数,初步评价其热安全性,为其在燃烧催化剂中的应用提供理论基础。

2 实验部分

2.1 试剂与仪器

1,1′-BTO,实验室自制,制备方法见文献[6]。

DSC: 823e差示扫描量热仪,瑞士METTLER TOLED公司。升温速率均为5,10,15,20 K·min-1,氮气气氛,流速30 mL·min-1,样品质量(0.2000±0.02) mg。TG: TGA/SDTA851e热分析仪,瑞士METTLER TOLED公司。升温速率为15 K·min-1,氮气气氛,流速30 mL·min-1,样品质量(0.2000±0.02) mg。

2.2 金属盐的合成

1,1′-BTOCo: 常温下,1,1′-BTO(0.51 g,0.003 mol)完全溶解于水中,搅拌下加入CoSO4·7H2O(0.68 g,0.003 mol),过滤得固体,乙醇和水洗进行提纯,过滤烘干,得粉色固体0.29 g,收率43.15%。IR(KBr,ν/cm-1): 1607,1437,1253,1183,1013,573; 元素分析(C2N8O2,%): 计算值,C 14.29,N 66.67; 实测值,C 14.15,N 65.97。

1,1′-BTOCu: 1,1′-BTO(0.51 g,0.003 mol)完全溶解于水中,加入CuSO4·5H2O(0.84 g,0.003 mol),用同样方法处理得淡绿色固体0.36 g,收率51.28%。IR(KBr,ν/cm-1): 1627,1439,1259,1190,1010,748,662; 元素分析(C2N8O2·2H2O,%): 计算值,C 11.76,H 1.96,N 54.90; 实测值,C 11.68,H 2.01,N 53.47。

1,1′-BTOPb: 1,1′-BTO(0.51 g,0.003 mol)完全溶解于水中,搅拌下加入自制Pb(NO3)2(0.76 g,0.003 mol)水溶液,同样方法处理得白色固体0.42 g,收率56.00%。IR(KBr,ν/cm-1): 1628,1406,1232,1169,991,728,578; 元素分析(C2N8O2·H2O,%): 计算值,C 12.90,H 1.08,N 60.22; 实测值,C 12.73,H 1.12,N 59.69。

X射线荧光光谱测定,1,1′-BTOCo,1,1′-BTOCu,1,1′-BTOPb中分别含有金属Co、Cu、Pb。三种盐等质量测试,理论值: CoO 25.65,CuO 27.18,PbO 47.17; 实测值: CoO 25.80,CuO 28.85,PbO 44.59。

2.3 结果与讨论

1,1′-BTOCo、1,1′-BTOCu、1,1′-BTOPb在升温速率为5，10，15，20 K·min-1下的DSC曲线如图1、图3和图5所示。升温速率为15 K·min-1下1,1′-BTOCo、1,1′-BTOCu、1,1′-BTOPb的TG-DTG曲线如图2、图4和图6所示。从DSC曲线可知,三种盐各自随着升温速率的增加,DSC放热峰向高温方向移动。1,1′-BTOCo的TG曲线(图2)在475 K之前有一定质量损失,但对应DSC曲线(图1)无吸热峰,所以为失去游离水阶段; 1,1′-BTOCu 的TG曲线(图4)在400 K之前有明显质量损失,对应DSC曲线(图3)有吸热峰,所以为失去结晶水水阶段; 1,1′-BTOPb的TG曲线(图6)在370 K之前有明显质量损失,对应DSC曲线(图5)有吸热峰,所以为失去结晶水水阶段。

图11,1′-BTOCo在不同升温速率下的DSC曲线

Fig.1DSC curves of 1,1′-BTOCo at different heating rates

图215 K·min-1时1,1′-BTOCo的TG-DTG曲线

Fig.2TG-DTG curves of 1,1′-BTOCo at 15 K·min-1

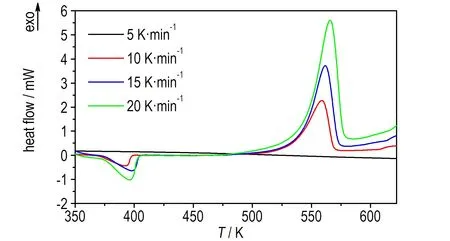
图31,1′-BTOCu在不同升温速率下的DSC曲线

Fig.3DSC curves of 1,1′-BTOCu at different heating rates

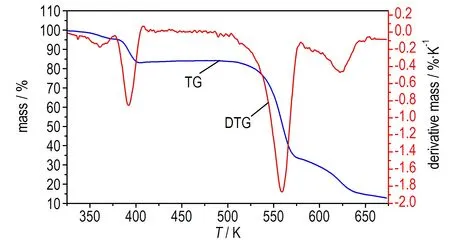
图415 K·min-1时1,1′-BTOCu的TG-DTG曲线

Fig.4TG-DTG curves of 1,1′-BTOCu at 15 K·min-1

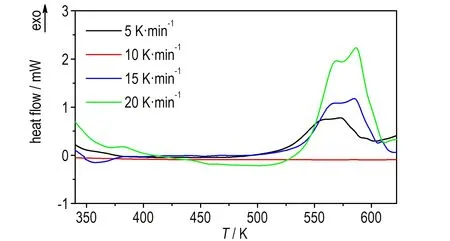
图51,1′-BTOPb在不同升温速率下的DSC曲线

Fig.5DSC curves of 1,1′-BTOPb at different heating rates

图615 K·min-1时1,1′-BTOPb的TG-DTG曲线

Fig.6TG-DTG curves of 1,1′-BTOPb at 15 K·min-1

3 结果与讨论

3.1 动力学参数计算

不同升温速率下(5、10、15,20 K·min-1)三种盐到热分解特征参数,见表1。用Kissinger法[7]和Ozawa法[8-9]求得表观活化能(EK和EO)、指前因子(AK),见表1。

对于炸药的热分解,用非等温法做热分解动力学研究时,常用的Ozawa公式为[8-9]:

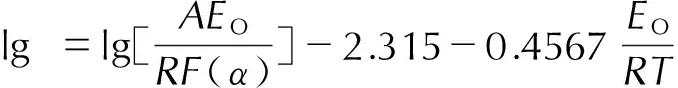
(1)

式中,α为炸药反应深度,%;R为理想气体常数,8.314 J·mol-1·K-1;β为升温速率,K·min-1;T为温度,K;A为指前因子, s-1;EO为表观活化能,J·mol-1·K-1;F(α)为机理函数的积分形式。

若选择相同的α,lgβ与1/T呈线性关系,由直线的斜率计算活化能,并用来求解热分解的机理函数。

根据Doyle法[9],式(1)可以变换为:

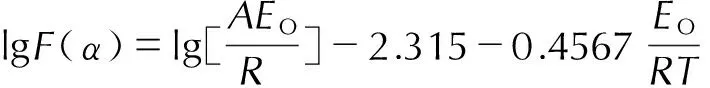
(2)

在式(2)中,对于任何热分解的机理函数,lgF(α)与1/T呈线性关系。对于某个假设的反应机理函数,若通过Doyle法求解得到的热分解活化能与Ozawa法求得的活化能接近,且线性相关系数好,由此获得热分解的反应机理函数[10]。

表1不同升温速率下DSC曲线得到的参数值

Table1The parameters determined by DSC curves at different heating rates

compoundβ/K·min-1Te/KTp/KΔHd/J·g-1Kissinger'smethodEK/kJ·mol-1AK/s-1Ozawa'smethodEO/kJ·mol-11,1'-BTOCo5511.26539.261181.3610503.04548.331603.1115508.98554.931835.0720528.26559.471173.29162.351.83×1015164.821,1'-BTOCu5527.61547.881173.2910533.29556.751228.8215539.96559.811564.8520542.98563.761342.24217.952.58×1020208.101,1'-BTOPb5529.34558.731491.6710534.19561.151274.1415539.39568.281113.3320543.91572.821189.17223.524.24×1020239.56

Note:Teis extrapolated onset temperature;Tpis the first temperature of exothermic peak; ΔHdis decomposition enthalpy;Ais pre-exponential constant;Eis Apparent activation energy; Subscript K, data obtained by Kissinger′s method; Subscript O, data obtained by Ozawa′s method.

根据升温速率分别为5,10,15,20 K·min-1时,1,1′-BTOCo热分解曲线,分别求出反应深度α所对应的反应温度T。根据公式(1)和实验数据对lgβ与1/T进行线性拟合,由直线斜率计算得表观活化能EO,见表2。根据公式(2)用Doyle法对假设的炸药分解反应的机理函数相应lgF(α)与1/T进行线性回归分析,结果见表3。线性拟合结果表明,1,1′-BTOCo在反应深度为0.2～0.6的阶段,热分解属于相边界反应(一维),R1,n=1机理。反应机理的微分形式为f(α)=α,热分解动力学方程为:

(3)

(4)

用同样的方法得到1,1′-BTOPb的表观活化能EO,见表6,并进行线性回归分析,计算结果见表7。线性拟合结果表明,铅盐热分解第一阶段,即反应深度为0.3～0.5的阶段,热分解属于一维扩散,1D,D1减速型α-t曲线机理。反应机理的微分形式为f(α)=α2,热分解动力学方程为:

(5)

3.2 热爆炸临界温度

自加速分解温度(TSADT)的计算,依据表1,按照文献[7,10-11],由式(6)计算得β→0时的Te0和Tp0。

(6)

式中,βi为试样升温速率,K·min-1;To0、Te0和Tp0分别为β→0时的T0、Te和Tp值,K。

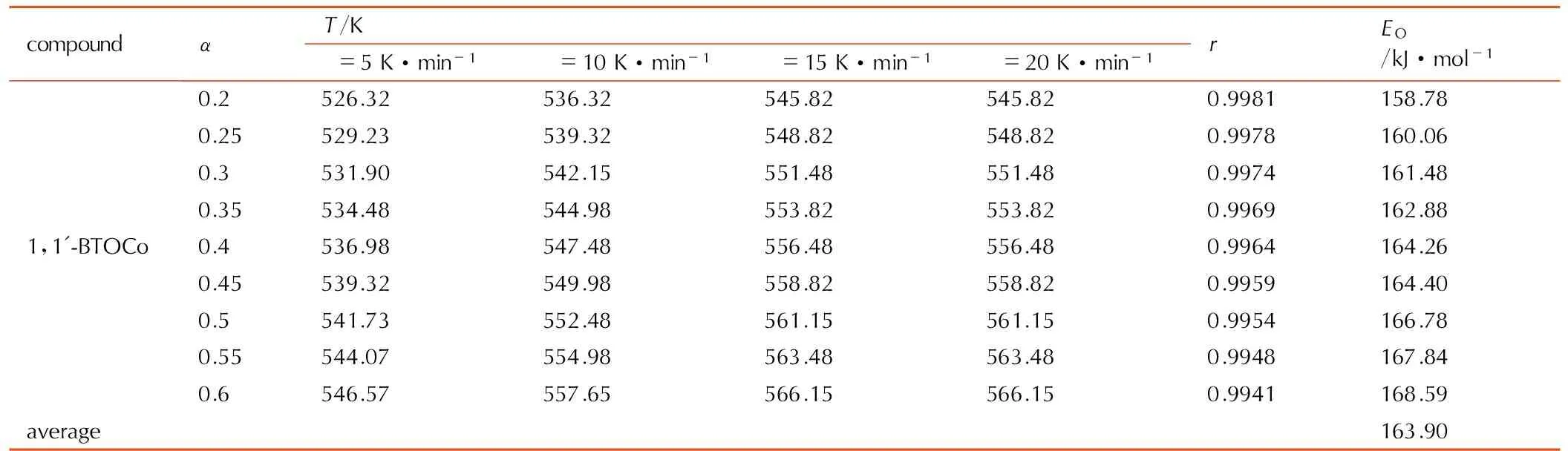
表21,1′-BTOCo的热分解反应活化能计算数据

Table2Calculated data of the activation energy for thermal decomposition reaction of 1,1′-BTOCo

compoundαT/Kβ=5K·min-1β=10K·min-1β=15K·min-1β=20K·min-1rEO/kJ·mol-11,1'-BTOCo0.2526.32536.32545.82545.820.9981158.780.25529.23539.32548.82548.820.9978160.060.3531.90542.15551.48551.480.9974161.480.35534.48544.98553.82553.820.9969162.880.4536.98547.48556.48556.480.9964164.260.45539.32549.98558.82558.820.9959164.400.5541.73552.48561.15561.150.9954166.780.55544.07554.98563.48563.480.9948167.840.6546.57557.65566.15566.150.9941168.59average163.90

Note:αis depth of reaction;Eis apparent activation energy; Subscript O, data obtained by Ozawa′s method.

表31,1′-BTOCo的lgF(α)-1/T的线性拟合结果

Table3Liner fitting results of lgF(α)-1/Tfor 1,1′-BTOCo

compoundβ/K·min-1interceptslopeDoyle'smethodr2Ed/kJ·mol-1Ad/s-1Ozawa'smethodEO/kJ·mol-11,1'-BTOCo516.5185-9210.16670.9799167.671.41×10151015.8778-9040.33600.9785164.576.61×10141516.4833-9479.43930.9772172.572.51×10152017.0773-9855.66270.9776179.429.55×1015163.90average171.062.57×1015

Note:Adis pre-exponential constant;Eis apparent activation energy; Subscript d, data obtained by Doyle′s method; Subscript O, data obtained by Ozawa′s method.

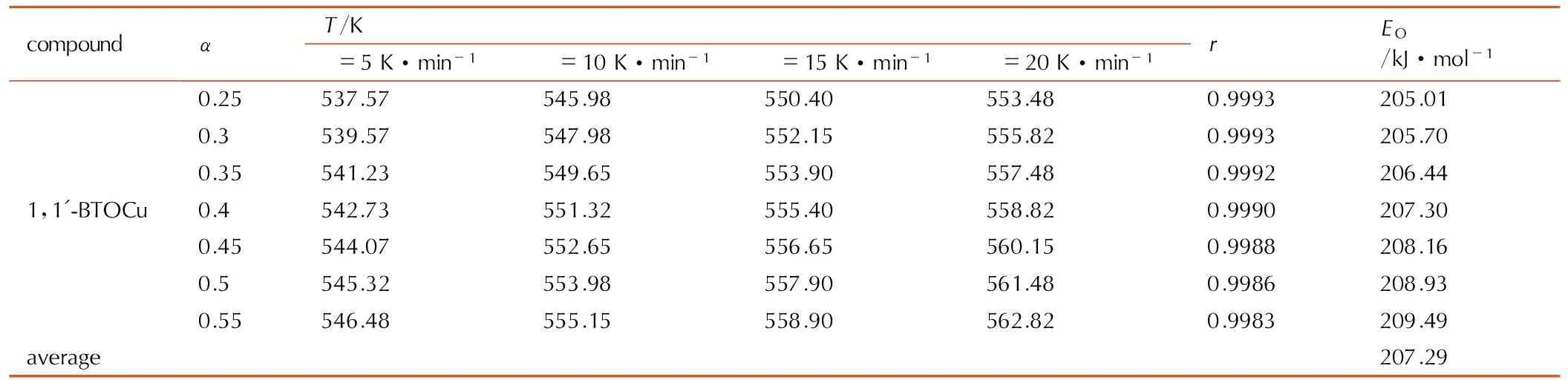
表41′-BTOCu的热分解反应活化能计算数据

Table4Calculated data of the activation energy for thermal decomposition reaction of 1,1′-BTOCu

compoundαT/Kβ=5K·min-1β=10K·min-1β=15K·min-1β=20K·min-1rEO/kJ·mol-11,1'-BTOCu0.25537.57545.98550.40553.480.9993205.010.3539.57547.98552.15555.820.9993205.700.35541.23549.65553.90557.480.9992206.440.4542.73551.32555.40558.820.9990207.300.45544.07552.65556.65560.150.9988208.160.5545.32553.98557.90561.480.9986208.930.55546.48555.15558.90562.820.9983209.49average207.29

表51,1′-BTOCu的lgF(α)-1/T的线性拟合结果

Table5Liner fitting result of lgF(α)-1/Tfor 1,1′-BTOCu

compoundβ/K·min-1interceptslopeDoyle'smethodr2Ed/kJ·mol-1Ad/s-1Ozawa'smethodEO/kJ·mol-11,1'-BTOCu520.7760-11391.66080.9986207.382.45×10191020.1870-11246.71020.9993204.741.29×10191521.7567-12201.37420.9988222.126.61×10202020.8558-11775.46120.9980214.371.15×1020207.29average212.157.08×1019

表61,1′-BTOPb的热分解反应活化能计算数据

Table6Calculated data of the activation energy for thermal decomposition reaction of 1,1′-BTOCu

compoundαT/Kβ=5K·min-1β=10K·min-1β=15K·min-1β=20K·min-1rEO/kJ·mol-11,1'-BTOPb0.30552.15559.15564.15566.820.9994234.550.35554.57561.65566.40569.150.9992237.570.40556.98564.15568.90571.480.9989239.240.45559.23566.65571.40573.820.9986239.920.50561.57568.98573.90576.150.9982240.43average238.34

表71,1′-BTOPb的lgF(α)-1/T的线性拟合结果

Table7Liner fitting results of lgF(α)-1/Tfor 1,1′-BTOCu

compoundβ/K·min-1interceptslopeDoyle'smethodr2Ed/kJ·mol-1Ad/s-1Ozawa'smethodEO/kJ·mol-11,1'-BTOPb522.9920-13257.47430.9920241.353.47×10211022.3470-13065.49960.9932237.851.62×10211522.2574-13126.77810.9892238.971.95×10212023.7608-14044.27300.9914255.677.76×1022238.34average243.465.37×1021

又根据TSADT=Te0,计算可得1,1′-BTOCo的TSADT=534.46 K,Tp0=527.31 K; 1,1′-BTOCu的TSADT=527.56 K,Tp0=526.50 K; 1,1′-BTOPb的TSADT=525.87 K,Tp0=568.32 K。

爆炸临界温度(Tbpo)的计算,根据Zhang-Hu-Xie-Li法,将表2中Ozawa法得到的EO和Tp0代入式(7)。

(7)

计算可得1,1′-BTOCo的Tbpo=542.22 K,1,1′-BTOCu的Tbpo=539.11 K,1,1′-BTOPb的Tbpo=580.00 K。

3.3 热力学参数

计算热力学参数,包括自由能ΔG≠,活化焓ΔH≠和活化熵ΔS≠,根据文献[12]按式(8)～(10)计算:

(8)

ΔH≠=Ek-RTp0

(9)

ΔG≠=ΔH≠-Tp0ΔS≠

(10)

式中,kB为Boltzmann常数,1.3807×10-23J·K-1;h为Plank常数,6.626×10-34J·K-1;EK为表观活化能,J·mol-1;AK为指前因子,s-1。

计算可得1,1′-BTOCo的ΔG≠=139.92 kJ·mol-1,ΔH≠=157.97 kJ·mol-1,ΔS≠= 34.23 J·mol-1; 1,1′-BTOCu的ΔG≠=143.51 kJ·mol-1,ΔH≠=213.56 kJ·mol-1,ΔS≠=132.98 J·mol-1; 1,1′-BTOPb的ΔG≠=141.34 kJ·mol-1,ΔH≠= 218.79 kJ·mol-1,ΔS≠=136.28 J·mol-1。

4 结 论

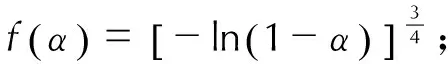
(2) 三种盐的自加速分解温度和热爆炸临界温度数值均较高,且焓变较大,说明三种盐热安定性好,尤其是常温下不易发生热分解。对于表观活化能,1,1′-BTOCo<1,1′-BTOCu<1,1′-BTOPb; 对于指前因子,1,1′-BTOCo<1,1′-BTOCu<1,1′-BTOPb。

参考文献:

[1] 王雅乐, 卫芝贤, 康丽, 等. 固体推进剂用燃烧催化剂的研究进展[J]. 含能材料, 2015, 23(1): 89-98.

WANG Ya-le, WEI Zhi-xian, KANG Li, et al. Progress on combustion catalysts of solid propellant[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2015, 23(1): 89-98.

[2] 张超, 杨立波, 陈俊波, 等. 含咪唑类铅盐催化剂的RDX-CMDB推进剂燃烧性能[J]. 含能材料, 2015, 23(1): 43-47.

ZHANG Chao, YANG Li-bo, CHEN Jun-bo, et al. Combustion performances of RDX-CMDB propellant with imidazoles lead salt catalyst[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2015, 23(1): 43-47.

[3] 汪营磊, 赵凤起, 仪建华. 固体火箭推进剂用燃烧催化剂研究新进展[J]. 火炸药学报, 2012, 35(5): 1-5.

WANG Ying-lei, ZHAO Feng-qi, YI Jian-hua. New progress of study on combustion catalysts used for solid rocket propellants[J].ChineseJournalofExplosives&Propellants, 2012, 35(5): 1-5.

[4] 张国涛, 周遵宁, 张同来, 等. 固体推进剂含能催化剂研究进展[J]. 固体火箭技术, 2011, 34(3): 319-323.

ZHANG Guo-tao, ZHOU Zun-ning, ZHANG Tong-lai, et al. Advances on energetic catalysts for solid propellant[J].JournalSolidRocketTechnology, 2011, 34(3): 319-323.

[5] Li W, Ren Y H, Zhao F Q, et al. Effects of lead complex-based BTATz on thermal behaviors, non-isothermal kinetics and combustion properties of DB/RDX-CMDB propellants[J].ActaPhysico-Chimica, 2013, 29(10): 2087-2094.

[6] Tselinskii I V, Mel′nikova S F, Romanova T V. Synthesis and reactivity of carhohydroximoyl azides: I.aliphatic and aromatic carbohydroximoyl azides and 5-substituted 1-hydroxyl-tetrazolesbasedthereon[J].RussianJournalofOrganicChemistry, 2001, 37(3): 430-436.

[7] Kissinger H E. Reaction kinetics in differential thermal analysis[J].AnalyticalChemistry,1957, 29 (11): 1702-1706.

[8] 何志伟, 高大元, 刘祖亮. 2,6-二氨基-3,5-二硝基吡啶-1-氧化物及其黏结炸药的热分解动力学[J]. 火炸药报, 2009, 32(2): 32 -35.

HE Zhi-wei, GAO Da-yuan, LIU Zu-liang. Thermal decomposition kinetics of 2,6-diamino-3,5-dinitropyridine-1-oxide and its formulation explosives[J].ChineseJournalofExplosives&Propellants, 2009, 32(2): 32-35.

[9] 马晓明, 李斌栋, 吕春绪, 等. 无氯TATB的合成及其热分解动力学[J]. 火炸药学报, 2009, 32(6): 24-27.

MA Xiao-ming, LI Bin-dong, Lü Chun-xu, et al. Synthesis and thermal decomposition kinetics of TATB without chloride[J].ChineseJournalofExplosives&Propellants, 2009, 32(6): 24-27.

[10] Ozawa T B.A new method of analyzing thermogravimetric data[J].BullChemSocJpn, 1965, 38(11): 1881-1886.

[11] 胡荣祖, 高胜利, 赵凤起, 等. 热分析动力学[M]. 第2版. 北京: 科学出版社, 2008: 151-155.

HU Rong-zu, GAO Sheng-li, ZHAO Feng-qi, et al. Thermal Analysis Kinetics[M]. 2nd Ed. Beijing: Science Press, 2008: 151-155.

[12] 胡荣祖, 高胜利, 赵凤起, 等. 1,1′-二甲基-5,5′-偶氮四唑一水合物和2,2′-二甲基-5,5′-偶氮四唑的热安全性[J]. 含能材料, 2011, 19(2): 126-131.

HU Rong-zu, GAO Sheng-li, ZHAO Feng-qi, et al. Thermal safety of 1,1′-dimethyl-5,5′-azotetrazole and 2,2′-dimethyl-5,5′-azotetrazole[J].ChineseJournalofEnergeticMaterials(HannengCailiao), 2011, 19(2): 126-131.