交流传动电力机车车网电压低频振荡分析
林 飞, 连巧娜,杨中平, 焦京海, 张志强
(1.北京交通大学 电气工程学院,北京 100044;2.南车青岛四方机车车辆股份有限公司,山东 青岛 266000)
在交流传动电力机车中,单相四象限变流器作为AC-DC环节,具有功率因数高、交流电流谐波低等优点,但也出现了由于车网耦合参数不当而造成的高频谐振或低频振荡等新问题[1-3]。其中,当有多台车共同运行在同一地点时,出现过牵引网电压及车上牵引传动系统直流环节电压的低频振荡现象。例如:2007年太原铁路局湖东机务段6台HXD1同时投入运行时出现了牵引传动系统直流电压振荡,7台同时投入运行时低频振荡增大导致列车牵引变流器直流环节过压保护动作,变流器封锁脉冲[2]。2010年9月,北京、沈阳等地的动车所均出现CRH5型动车组由于网压出现5 Hz左右的低频振荡而导致牵引封锁、列车无法出发的现象[3]。
国内外对多车系统低频振荡问题展开了深入研究。文献[2-7]对多台列车接入电网时出现的低频振荡现象进行了分析,认为列车台数n的增加会改变牵引网的等效阻抗,造成了车网阻抗不匹配从而引起系统振荡。文献[8]通过建立四象限变流器状态变量之间的函数关系,根据特征值的特性研究控制参数对低频振荡的影响。文献[9]根据稳态功率守恒推导出了直流电压环节控制系统闭环传递函数,认为车网间低频振荡主要与电压环比例系数有关。但由于四象限变流器为较复杂的非线性系统,目前尚未对车网电压低频振荡的产生及振荡频率进行定量分析。
针对四象限变流器的系统建模,文献[10]基于状态空间平均模型及输出波形特点,提出了适用于建立系统控制模型的平均值分离法和半周期平均法,进而线性化后得到有关变流器的传递函数模型。文献[11]针对四象限变流器的时变特性,采用将输入电流、电压等交流稳态值进行正、余弦分解的方法消除了系统方程的时变特性,进而利用小信号方法推导出包含直流环节电压控制外环的传递函数。文献[12]利用电压平方控制的方法推导出四象限变流器的大范围线性化模型,规避了非线性系统近似线性化的复杂过程以及建模偏差。文献[13]主要针对多逆变器并网问题进行建模研究,建立了包含电压源、电流源的变流器等效模型,最终与电网等效阻抗电路构成级联系统,运用阻抗比判据及数值仿真研究了系统稳定性。本文在此基础上基于系统输入输出的瞬态功率守恒,建立车网耦合系统小信号模型,针对系统的阻尼比、振荡频率与控制参数的关系,分析系统低频振荡的产生原因及影响因素,并提出改善多车系统低频振荡的建议。
1 车网系统电路模型分析
1.1 车网系统的数学模型
为了方便分析多车运行时系统的稳定性,假设同一供电臂下某点有n台列车,且所有车的电流均同步,此时网侧线路阻抗的压降是单车运行时的n倍,因此可等效为单车情况时,线路等效线路阻抗Zl扩大为原来的n倍[2],此时的等效模型如图1所示。

图1 多车系统等效为单车时车网模型
将牵引供电系统考虑在内的四象限变流器的等效电路如图2所示。其中,us是牵引变电所折算到机车变压器副边的电压值,假设为理想电压源;Zs是牵引变电所阻抗及牵引变电所到机车接入端口的线路阻抗折算到变压器副边的阻抗;Lm是变压器(含四象限变流器交流电抗器)折算到变压器副边的感抗;R是牵引电机-逆变器在直流侧的等效负载;uin是受电弓处电压折算到变压器副边的等效电压;im是四象限变流器的输入电流;uab为四象限变流器交流侧的电压;ud为直流侧电压;id为直流侧电流。

图2 牵引传动系统等效电路图
四象限变流器在双极性调制下存在两种工作模态:模态1,T1与T4导通,T2与T3截止,ab端线电压uab为ud;模态2,T2与T3导通,T1与T4截止,ab端线电压uab为(-ud)。模态1的状态方程为
( 1 )
模态2的状态方程为
( 2 )
1.2 车网系统的控制模型


图3 四象限变流器瞬态电流控制策略框图
忽略PWM开关周期内系统的动态变化及其产生的高次谐波,只考虑PWM过程中调制波基波(设调制度为m)的作用,将1.1节提到的模态1与模态2进行合并,即

( 3 )
( 4 )

( 5 )
将式( 3 )代入式( 5 ),可得
( 6 )


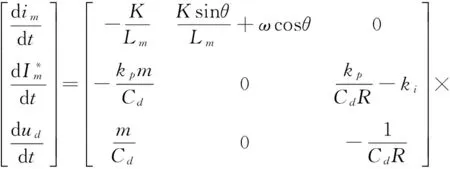
( 7 )
由于系统的状态矩阵含有时变量θ和状态变量函数m,系统存在时变性和强非线性,不利于系统性能的分析。
1.3 车网系统模型的线性化
为此,需将系统在平衡点附近进行线性化。系统平衡点为
( 8 )
式中:ua为直流环节二次脉动的幅值;δ为二次脉动电压的相位角;P1为四象限变流器稳态有功功率。
为了得到系统的控制函数,根据IGBT桥臂输入侧与输出侧瞬时功率相等的原则,可得各变量幅值的关系为
uab×im=mud×im=ud×id
( 9 )
(10)
其中
(11)
式中:φ为变电所电压与网侧电流之间的相角;Rs、Ls分别为牵引变电所及牵引网阻抗折算到变压器副边的电阻和电感。
考虑在系统平衡点附近,式(10)可以表示为

(12)
同时,四象限变流器直流环节支撑电容与电阻并联,有
(13)
忽略式(12)中二倍工频交流分量,交流侧电流幅值与直流环节电压微变量关系可以表示为

(14)
四象限变流器的小信号模型可以表示为
(15)
基于图2电路拓扑,交流侧电流的幅值以及相位角均随列车台数n变化,根据图4所示交流侧电压电流之间的相量关系以及系统有功功率守恒,可求取Im和cosφ。

图4 交流侧电压、电流相量图
(16)
式中:P2为牵引变电所及牵引网阻抗消耗的有功功率。
交流电流幅值Im可以表示为

(17)
将式(17)代入式(16)中求取交流侧电压电流之间的相位关系,进而为下文的稳定性分析提供支撑。


图5 线性化后得到的闭环系统框图
闭环系统特征多项式为
G(s)=as3+bs2+cs+d
(18)
其中
(19)
2 系统低频振荡的机理
多车系统的振荡与闭环系统的阻尼比[17]有着密切关系。对于式(18)所示的三阶系统,其3个极点可以分别表示为x1=λ,x2=A+jB,x3=A-jB。
根据三角函数法,式(18)所对应的三个极点分别为
(20)
其中
(21)


图6 n=1~n=10的系统极点分布图
根据式(22)、式(23)可以求出系统阻尼比ξ与振荡频率ω。
(22)
(23)

图7 n=1~n=10的系统主导极点分布图
依据式(20),在某些控制参数下,随着列车增多,系统主导极点向复平面的右半平面移动,系统阻尼比下降,如图7所示(图6虚线处放大),严重时甚至为负,系统会产生振荡。根据式(22)和式(23),系统的阻尼比及振荡频率与四象限变流器电压环的控制参数也有密切关系。如图7所示,电压环比例系数kp越大,积分时间常数τ越小,则系统阻尼比越小。故列车数目n、电压环控制器的PI参数均是振荡特性的重要影响因素,其中PI参数影响相对较大。而由图8同样可知,在运行列车台数一定时,若电压环控制参数恰当,可增大系统阻尼比,进而抑制系统的振荡。

图8 n=5时,阻尼比与控制参数之间的关系
依据式(23),如图9所示,振荡频率随控制参数变化明显,但振荡频率一直都处于基波频率之下,故由于系统阻尼过低而引起的振荡均为低频振荡,与事故现象一致。

图9 n=5时,振荡频率与控制参数之间的关系
本节中通过研究低频振荡机理,表明多车系统时电压环控制参数设置不当可能造成系统产生低频振荡。而一旦直流侧电压振荡幅值超出了保护阈值,将导致牵引封锁,对铁路的运营造成很大影响。通过设置适当的电压环控制参数可提高系统的稳定性。
3 实验验证
在实验室对前文的理论分析进行了实验验证,实验参数见表1。

表1 实验平台的四象限变流器及线路参数表
在未加入线路等效电感Ls时,视为单车情况,而加入线路等效电感Ls,来近似模拟多车系统时线路阻抗加大的情况。根据表1参数,按照上述理论公式进行计算可知:
(1)如图10所示,相同控制参数时,多车系统的主导极点位于s平面的右半平面,由于四象限变流器的非线性因素,系统会发生2.2 Hz左右(图11数据显示)的持续振荡,较单车系统稳定性差。
(2)如图11所示,多车系统发生低频振荡时,可以通过调整电压环控制参数,增大系统阻尼,使失稳系统恢复稳定。

图10 kp=1.8,τ=0.228,单车与多车系统的主导极点分布对比图

图11 控制参数调整前后,多车系统主导极点分布对比图
未加入线路等效电感LS时,即单车情况下,实验平台结果如图12所示。

图12 kp=1.8,τ=0.228,单车时直流侧电压ud、交流电压uin、交流电流im的波形
可见,单车时直流电压保持稳定,网压与网流相位一致,控制性能较好。
而相同控制参数下,接入线路等效电感Ls后,即模拟多车情况下的实验结果如图13所示。可见,此时直流侧电压和交流电流幅值出现了约为2 Hz的明显振荡。此结果与图11数据显示的理论分析结果基本吻合。

图13 kp=1.8,τ=0.228,多车时直流侧电压ud、交流电压uin、交流电流im的波形
保持其他系统参数不变,在图13的控制参数基础上,只调小kp或仅增大τ,系统恢复稳定,结果分别如图14和图15所示。
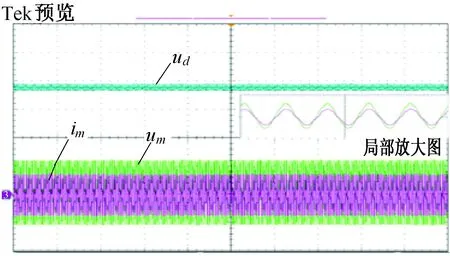
图14 kp=1.2,τ=0.228,多车时直流侧电压ud、交流电压uin、交流电流im的波形

图15 kp=1.8,τ=0.285,多车时直流侧电压ud、交流电压uin、交流电流im的波形
实验结果同样验证了前面的理论分析,电压环控制参数设置不当时,列车运行台数增多会导致系统低频振荡,但是通过调整控制参数可以使系统稳定性有较好的改善。
4 结论
本文基于单相四象限变流器,建立多车系统车网耦合等效模型,利用系统的阻尼比解释了多车系统低频振荡机理,分析结果表明列车数目及四象限变流器的电压环控制参数对系统稳定性影响较大。一般情况下,通过调节电压环控制参数可以使车网系统重新获得稳定。本文的分析为进一步研究列车低频振荡的影响因素以及如何避免这些影响提供重要的参考,为保证多台列车稳定运行提供了理论支撑。
参考文献:
[1]LIU J, YANG Q, ZHENG T Q. Harmonic Analysis of Traction Networks Based on the CRH380 Series Emus Accident[C]//IEEE Transportation Electrification Conference and Expo. New York: IEEE Press, 2012:1-6.
[2]郑琼林. HXD1交流传动电力机车谐振原因分析与对策[J].变频器世界,2009(5): 40-44.
ZHENG Qionglin. A Probe on Causes and Solution of the HXD1 AC Locomotive’s Resonance[J]. The World of Inverters, 2009(5): 40-44.
[3]王晖, 吴命利. 动车组引起牵引供电系统网压低频振荡现象测试及分析[C] //中国高等学校电力系统及其自动化专业学术年会,2011.
[4]MOLLERSTEDT E, BERNHARDSSON B. Out of Control Because of Harmonics-An Analysis of the Harmonic Response of an Inverter Locomotive[J].Control Systems, 2000, 20(4):70-81.
[5]BARTELT R, OETTMEIER M, HEISING C, et al. Improvement of Low-frequency System Stability in 16.7 Hz Railway-Power Grids by Multivariable Line-Converter Control in a Multiple Traction-Vehicle Scenario[C]//Electrical Systems for Aircraft, Railway and Ship Propulsion. New York: IEEE Press, 2010.
[6]HEISING C, BARTELT R, OETTMEIER M, et al. Improvement of Low-frequency System Stability in 50 Hz Railway-Power Grids by Multivariable Line-Converter Control in a Distance-Variation Scenario[C]// Electrical Systems for Aircraft Railway and Ship Propulsion. New York: IEEE Press, 2010.
[7]HEISING C, BARTELT R, OETTMEIER M, et al. Enhancement of Low-frequency System Stability of 60 Hz Railway Power Grids[C]//International Power Electronics and Motion Control Conference. New York: IEEE Press, 2010.
[8]DANIELSEN S, FOSSO O B, MOLINAS M, et al. Simplified Models of a Single-phase Power Electronic Inverter for Railway Power System Stability Analysis-Development and Evaluation[J]. Electric Power Systems Research, 2010, 80(2):204-214.
[9] 韩智玲, 唐蕾, 李伟. 交流传动电力机车车网电压不稳定的原因分析与解决[J]. 铁道学报, 2011, 33(10):25-28.
HAN Zhiling, TANG Lei, LI Wei. Causal Analysis and Resolution of the Voltage Instability between AC Drive Electric Locomotive and Power Supply Network[J].Journal of the China Railway Society, 2011,33(10): 25-28.
[10]张加胜, 李浩光. 单相PWM可逆整流器的动态控制建模方法[J]. 电力电子技术, 2008, 42(3):66-68.
ZHANG Jiasheng, LI Haoguang. Method on Dynamic Control Modeling of Single Phase PWM Reversible Rectifiers[J]. Power Electronics,2008,42(3):66-68.
[11]BRENNA M, FOIADELLI F, ZANINELLI D. New Stability Analysis for Tuning PI Controller of Power Converters in Railway Application[J]. Industrial Electronics IEEE Transactions on, 2011, 58(2):533-543.
[12]HE L, XIONG J, OUYANG H, et al. High-performance Indirect Current Control Scheme for Railway Traction Four-quadrant Converters[J]. IEEE Transactions on Industrial Electronics, 2014, 61(12):6 645-6 654.
[13]许德志, 汪飞, 毛华龙,等. 多并网逆变器与电网的谐波交互建模与分析[J]. 中国电机工程学报, 2013, 33(12):64-71.
XU Dezhi, WANG Fei, MAO Hualong, et al. Modeling and Analysis of Harmonic Interaction between Multiple Grid-connected Inverters and the Utility Grid[J]. Proceedings of the CSEE, 2013, 33(12):64-71.
[14]郑俊, 冯晓云, 谢望玉,等. 单相PWM整流器瞬态电流控制策略的研究[J].电力电子技术, 2009, 43(12):2-3.
ZHENG Jun, FENG Xiaoyun, XIE Wangyu,et al. The Transient Current Control for Single Phase PWM Rectifiers[J].Power Electronics,2009, 43(12): 2-3.
[15]OETTMEIER M, HEISING C, STAUDT V, et al. Dead-beat Control Algorithm for Single-phase 50 kW AC Railway Grid Representation[J]. IEEE Transactions on Power Electronics, 2010, 25(5): 1184-1192.
[16] HEISING C, OETTMEIER M, BARTELT R, et al. Multivariable Pole-placement Control Design for a Single-Phase 50 kW, 16.7 Hz Railway Traction Line-side Converter[C] //International Conference on Power Engineering, Energy and Electrical Drives. New York: IEEE Press, 2009.
[17]胡寿松.自动控制原理[M].北京:科学出版社,2007:71-121.

