一种基于TC-CPN的城轨列车车门故障溯因诊断方法
沈碧波,佘 维,叶阳东,贾利民
(1.郑州大学 信息工程学院,河南 郑州 450001;2.郑州大学 软件学院,河南 郑州 450002;3.北京交通大学 轨道交通控制与安全国家重点实验室,北京 100044)
城市轨道交通作为支撑城市正常运行的大动脉,发展迅速。车门作为城轨列车的重要部件,既是乘客进出列车的通道,同时也是保障列车运行特别是乘客安全的关键,针对车门的故障诊断与隐患挖掘的研究具有重要意义。故障诊断是根据检测量所获得的故障表征以及系统故障源与其表征之间的映射关系,分析和定位故障源的过程。溯因推理[1]是一种对观测所得进行溯源的推理解释方法,主要研究形成观测现象的系统演化发展过程,在系统控制理论、自然语言解释以及运筹学等领域得到了非常广泛的应用。回溯推理不仅用于追溯状态产生的原因,还能对系统行为和事件发展过程进行解释。当系统处于某种稳定状态时,分析该状态的成因,对其进行回溯推理是许多实际应用中的必然需求[2-5]。通常可利用数据采集与监控系统(SCADA)获取系统的状态信息,并记录事件动作、顺序及时间特征[6]。状态信息的分析方法很多,如专家系统、人工神经网络、粗糙集、贝叶斯网络、遗传算法等,但也存在一定局限性。Petri网因其具有直观的图形化模型表达,严格的数学描述和推理证明,适合分析离散事件动态系统DEDS (Discrete Event Dynamic Systems)的行为,因而被广泛应用于交通、电力等领域的建模分析和故障诊断[7-9]。
自控网[10]系统中弧的权值可随某一库所内托肯数目动态变化,这也决定了自控网的非线性特性[11],使得自控系统无法直接套用其他网系统的分析技术。自控系统在模拟代数运算、控制系统建模问题方面有着较好的语义描述能力。文献[12] 提出扩展时段时序逻辑,引入时间Petri网模型,同时提出了几种变迁间的实施推理规则以简化复杂时序关系的Petri网模型,为进行线性推理提供了有利的工具。基于时间维度的分析常常能为系统行为的追溯提供另一层面的证据[13]。时间信息是自控系统行为的重要属性,直接影响系统的状态转移,将时间因素融入故障溯因诊断过程中,为正确诊断故障源提供了时间维度的证据。
本文针对城轨列车车门开门控制系统故障诊断问题,以自控Petri网为基础,结合文献[8,13]时间知识推理,提出一种时间约束自控Petri网TC-CPN(Cyber Petri Net of Time Constraint),该方法根据捕获的故障表征和SCADA采集的状态与时间信息,结合故障源与其表征间的映射关系,利用溯因推理进行故障诊断。给出时间约束自控Petri网的形式化定义及其状态转移规则,结合时间区间计算及区间关系判定方法,进一步提出故障溯因诊断方法,通过对列车车门故障算例的建模与分析,验证了该方法的有效性。
1 时间约束自控Petri网
定义一种时间约束自控Petri网TC-CPN(Cyber Petri Net of Time Constraint),图形示例如图1所示。
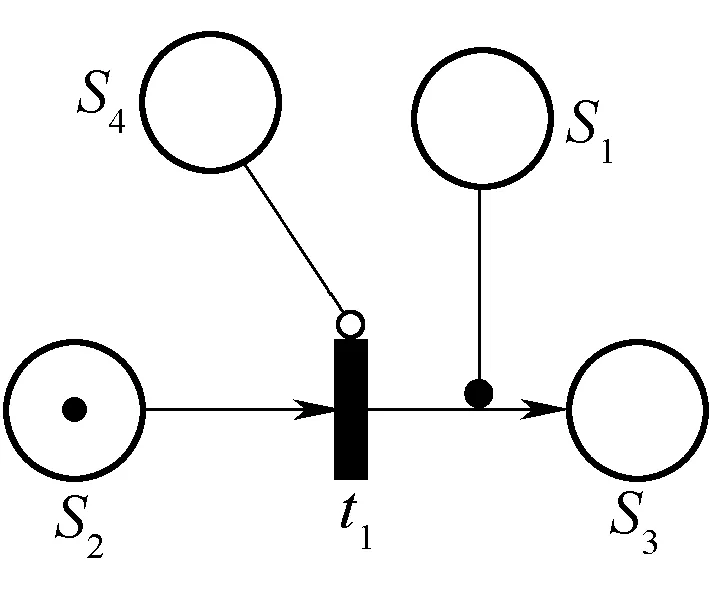
图1 时间约束自控Petri网
定义1一种时间约束自控Petri网TC-CPN是一个七元组∑TCC=(S,T;F,I,τ,W,C,M0),其中
(1)S={si|i∈N+}为库所的有限集,且满足∀s∈S:s∩s·∩(s·)·∩…=s*=Ø,s·表示s的直接后继节点,s*表示包含s本身在内的s的直接后继和间接后继的闭包集合。
(2)T={tj|j∈N+}为变迁的有限集。
(3)S∪T≠Ø,S∩T=Ø。
(4)F⊆((S×T)∪(T×S))为弧的有限集。(S,T;F)为有向网,称为∑TCC的基网。

(6)τ:T→R0×(R0∪{∞}),τ(ti)为变迁ti关联的时间区间。
(7)C:S→F为自控弧的有限集,自控弧(s,(x,y))的始端为库所s,末端指向受控弧(x,y)∈F。
(8)W为∑TCC的权函数,W(x,y)=s当且仅当(s,(x,y))∈C;非受控弧无特殊标识其权值为1。
(9)M0:S→0,1,2,…为∑TCC的初始状态标识。
定义2设∑TCC为一个TC-CPN,其状态转移规则为:
(1)映射M:S→0,1,2,…称为∑TCC的状态标识。
(2)令∀(x,y)∈((S×T)∪(T×S)),标识M下的权函数定义为
(3)变迁t∈T在标识M有发生权,即M[t>的条件是:①对于∀s∈S:M(s)≥WM(s,t),且有s∈·t,其中·t表示t的直接前继节点,使WM(s,t)>0,即t至少有一个非0的输入权;②若∃s∈S,(s,t)∈I:M(s)=0,即该变迁若有抑止弧与其相连,抑止条件不满足。必须同时满足上述两个条件,t才有发生权。
(4)若M[t>,则t可以发生,后继标识M′由下式给出:M′(s)=M(s)+WM(t,s)-WM(s,t),后继关系记作M[t>M′。
图1中尾部带空心圆圈的直线表示抑止弧,由库所s1发出的一个以实心圆为箭头的直线指向有向弧(t1,s3),表示库所s1中所含的托肯数为有向弧(t1,s3)的权值,记作W(t1,s3)=s1。
自控网系统的可变权与其动态行为有关,随系统状态变化的是库所中的托肯,用作可变权的正整数来自当前标识。仅以图1目前表示的Petri网的状态来看,该网并没有体现可变权,也没有自控能力,图1可视为某子系统,是从某个大系统中截取的一部分。根据变迁规则,若库所s4中有托肯,变迁t1被抑止,不能发生;若库所s4中没有托肯,t1可以发生:如果s1中没有托肯,那么t1发生将使得s2失去它唯一的托肯;如果s1从大系统中获得1个托肯,那么初始标识M0=(1,1,0,0)将由t1触发后继标识M1=(1,0,1,0),即起控制作用的库所s1中托肯保持,变迁t1的后继库所s3获得托肯,M1(s3)=M0(s3)+WM0(t1,s3)-WM0(s3,t1)=0+1-0=1。
定义3令牌和状态标识集:
用π(s)={λ1,λ2,…,λk}表示库所s中令牌的有限集,令牌λi以向量(rv,tm,{ev})表示。其中,rv∈{ε,-1,0,1}为令牌的标识,rv=ε表示库所内未采集到可观测的令牌,rv=1表示有确定观测时间区间的实令牌,rv=0表示观测为左闭右开时间区间的实令牌,rv=-1表示虚令牌;tm∈R0×R0表示令牌可能出现的时间区间,若tm标记为[ϖ,ϖ]则可表示任意时间区间;{ev}为令牌所携带的事件集,ev∈S×{0,1}表示某个事件。
用状态标识Mi对TC-CPN的动态行为进行描述,TC-CPN的每一个状态对应于库所的一个标识向量。采用集合{(s,π(s)}表示Mi,所有系统状态的集合记为M。若Mj通过变迁t的发生直接可达Mk,记为Mj[t>Mk。
定义4设时间区间tmi=[a,b],tmj=[c,d],定义两区间的加法运算为
tmi+tmj=[a+c,b+d]
( 1 )
减法运算为
tmi-tmj=[a-c,b-d]
( 2 )
定义区间关系判定函数
1.3.6 手术标准 均使用腹腔镜辅助下胃癌根治术,手术过程按照2007版《腹腔镜胃癌手术操作指南》[8]进行。

( 3 )
γ(tmi,tmj)=-1可解释为发生于tmi的事件绝对“早于”发生于tmj的事件;γ(tmi,tmj)=1可解释为发生于tmi的事件绝对“晚于”发生于tmj的事件;γ(tmi,tmj)=0可解释为发生于tmi的事件与发生于tmj的事件在时间轴上有交集,交集记为tmi⊕tmj。
设U={tm1,tm2,…,tmn}为时间区间的有限集,以tmL(U)=[alatest,blatest]表示U中的最迟时间区间,其中alatest≥ai,ai为U中任意元素的时间区间左端点,若ai为ϖ,忽略ai。
定义5设某两个令牌λi、λj的时间区间分量为tmi、tmj,过程时延区间为tmk,令牌时序一致性判定函数κ定义为
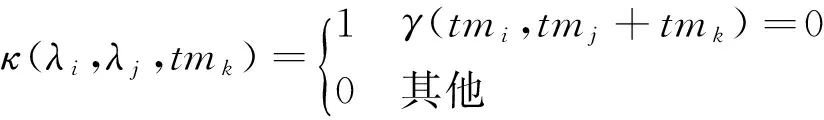
( 4 )
若κ(λi,λj)=1,则λi、λj存在时序一致性;反之,则不存在时序一致性。
2 溯因故障诊断方法
故障诊断实际上是依据检测量所获得的某些故障表征以及系统故障源与故障表征之间的映射关系,找出故障源的过程。在故障诊断领域,正向分析是故障传播的方向,这种故障传播网一般为无冲突无冲撞的纯网,而诊断推理是沿着传播模型的反方向追根溯源,挖掘隐患。
2.1 求逆算法
TC-CPN是一种分析具体问题的正向推理方法, 求其的逆网用作诊断模型。定义求逆过程算法如下,求逆操作示意图如图2所示。

算法1 ∑-1TCC=getInverseNet(∑TCC)输入:∑TCC———时间约束自控Petri网。输出:∑-1TCC———时间约束自控Petri网的逆网。1.S:=S';T:=T';I:=I';C=C';W:=W'//保留所有库所、变迁、抑止弧以及自控弧和各弧权值。2.F:={(x,y)|((y,x)∈F')∧((y,x)∉I)∧((s,(y,x))∉C)}//将∑TCC原有的弧均置为反向,抑止弧、自控弧除外。3.foreach t∈Tif τ'(t)=[a,b] then τ(t):=[-b,-a]//求逆得到t的时间区间τ。4.foreachM'0(s):s∈Sif s.tm0≠εthen s.rv0=1,λ0=(s.rv0,s.tm0,{ev0})π(s)=π(s)∪{λ0}//对每个库所检查,如果某库所s的观测值tm分量不为空,标记rv=1,并将令牌λ0置入库所s令牌的有限集π(s)中。5.return∑-1TCC=(S,T;F,I,τ,W,C,M0)

图2 求逆操作示意
2.2 溯因推理方法
根据故障告警信息的时序特征和因果关系,提出故障信息处理的 TC-CPN 溯因推理方法,其算法思想如下。
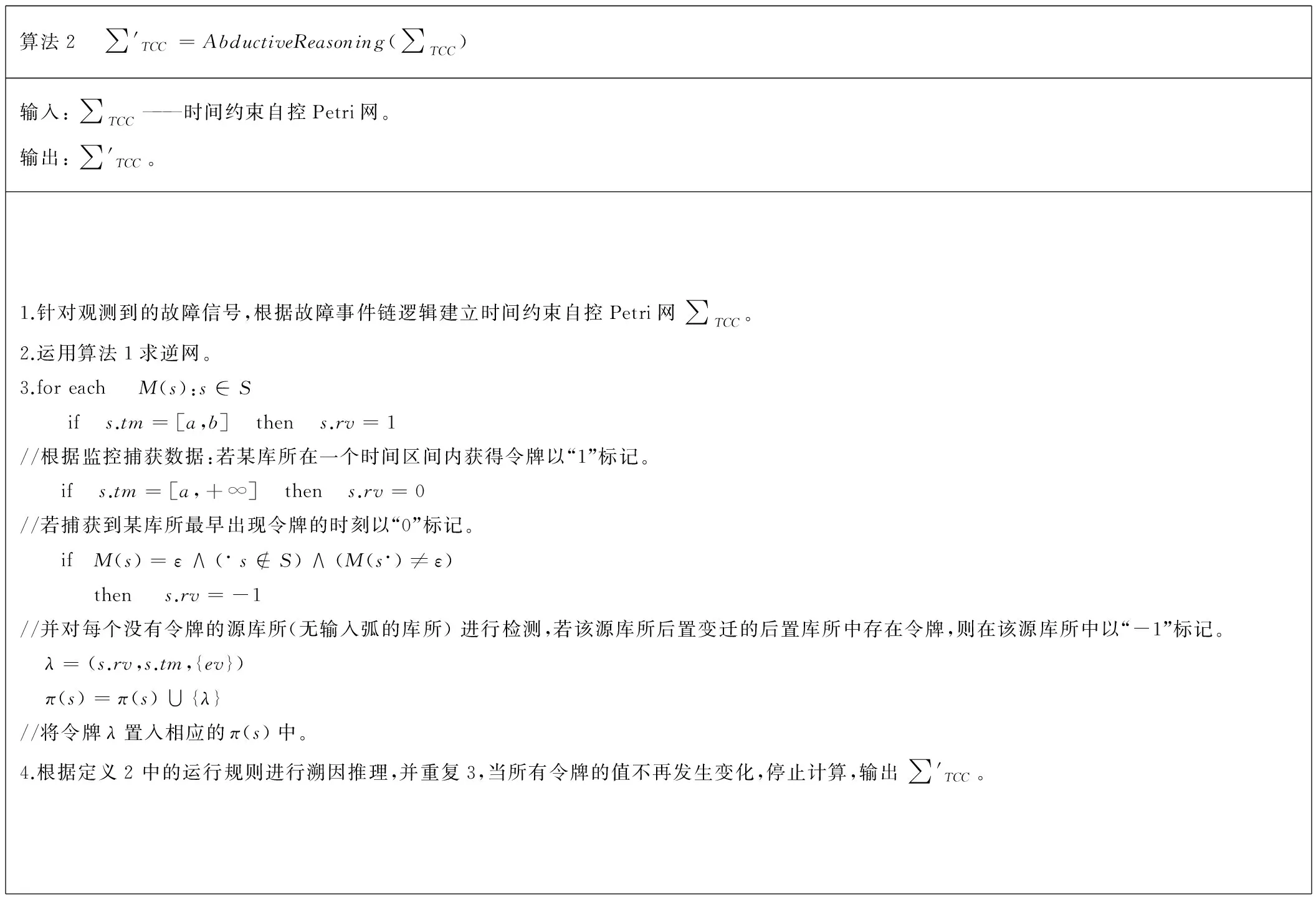
算法2 ∑'TCC=AbductiveReasoning(∑TCC)输入:∑TCC———时间约束自控Petri网。输出:∑'TCC。1.针对观测到的故障信号,根据故障事件链逻辑建立时间约束自控Petri网∑TCC。2.运用算法1求逆网。3.foreach M(s):s∈S if s.tm=[a,b] then s.rv=1//根据监控捕获数据:若某库所在一个时间区间内获得令牌以“1”标记。 if s.tm=[a,+∞] then s.rv=0//若捕获到某库所最早出现令牌的时刻以“0”标记。 if M(s)=ε∧(·s∉S)∧(M(s·)≠ε)then s.rv=-1//并对每个没有令牌的源库所(无输入弧的库所)进行检测,若该源库所后置变迁的后置库所中存在令牌,则在该源库所中以“-1”标记。 λ=(s.rv,s.tm,{ev}) π(s)=π(s)∪{λ}//将令牌λ置入相应的π(s)中。4.根据定义2中的运行规则进行溯因推理,并重复3,当所有令牌的值不再发生变化,停止计算,输出∑'TCC。
对确认的元件故障结合TC-CPN 进行分析,找出带有虚令牌且不含实令牌的库所。独立存在的虚令牌指示了误动、拒动、信息丢失等干扰因素。另外,冲突的令牌也蕴含了一些系统状态信息,如信息时标错误或虚警等。
3 实例分析
3.1 车门控制系统
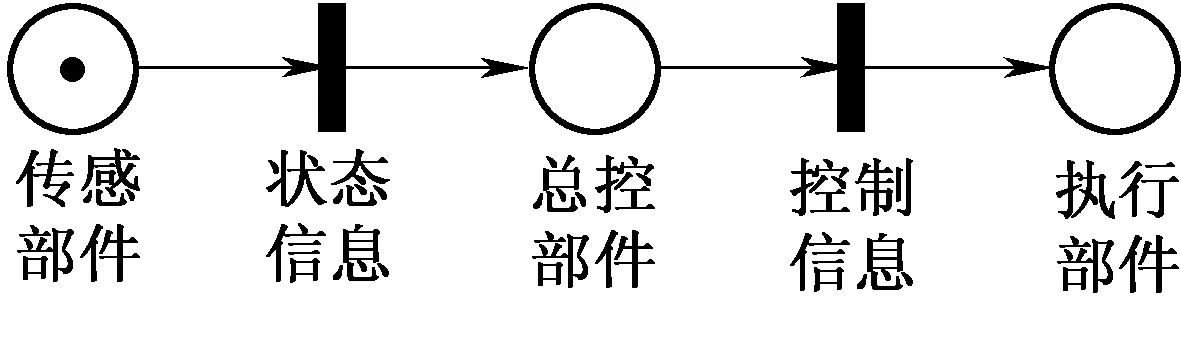
图3 控制过程示意图
车门系统模型的开门过程可以分为3个部分:电气控制、EDCU控制和机械动作。其中电气控制主要完成控制台发出开门信号和驱动电机运转的信号;EDCU控制主要完成EDCU与电机交互控制车门运动速度的信号;机械动作主要描述车门机械部件的动作过程。这3个层次的子网互相关联交互,共同控制车门系统的动作过程。
3.2 模型的建立
为了更好地说明问题,本文选取列车塞拉门开门过程核心部分(负责协调电气控制和EDCU控制,驱动电机运转,带动车门开启机械动作)的故障算例,分析说明具体的诊断过程。核心交互部分既涵盖了各种驱动信号的发出,又包含了与机械隔离装置的共同控制,体现了EDCU状态转换与机械动作的同步,是整个车门控制最核心的部分。
核心控制是在电气控制结束后EDCU得电开始,直到控制车门开始动作。此过程包含EDCU控制各部件动作(如控制发出电机驱动信号,允许车门动作控制信号),电机正常运转保证各部件按照EDCU控制要求正常动作(如锁闭装置打开等),锁闭装置状态监测与反馈(监测隔离装置是否有动作),机械动作开始后向EDCU发出状态反馈使EDCU转入下一状态同时车门动作开始。
由时间约束自控Petri网的形式化定义和本文所描述的EDCU控制过程,建立车门EDCU控制的扩展时间自控Petri网模型,如图4所示,各库所含义见表1。
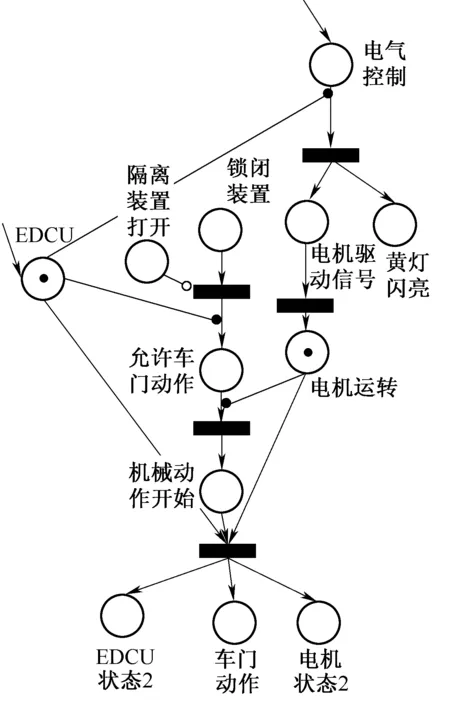
图4 TC-CPN模型图

标识含 义标识含 义s1EDCU控制状态s2EDCU状态2s3电气控制s4黄灯闪亮s5电机驱动信号s6电机运转s7锁闭装置s8隔离装置有动作s9允许车门动作s10机械动作开始s11车门动作s12电机运转状态2
模型说明:
(1)s3电气控制获得托肯表示车门控制系统中自控制台发出开门信号后一系列电气控制过程结束,系统将转入EDCU控制过程,假设电气过程无故障。
(2)EDCU是车门的控制部件,s1EDCU的托肯来自电气控制过程中EDCU得电,EDCU得电后才能正确控制开门过程。
(3)s7锁闭装置以及s8隔离装置有动作,两个库所状态由传感器探测得到,若锁闭装置正常,车门开始打开的瞬间,锁闭装置被机械打开;若隔离装置有动作则说明手动隔离装置被打开,被隔离的车门将不受EDCU控制,后续动作被抑止,车门无法正常打开和关闭。
(4)变迁t5表示同步,即在车门开始动作的同时使EDCU、电机转入下一阶段车门开始机械动作的状态。
3.3 算例
监控系统捕获如下信息:O(s1)=[110 ms,800 ms],O(s2)=800 ms,O(s4)=228 ms,O(s6)=[850 ms,1 000 ms],O(s7)=170 ms,其中O(x)表示最早捕获到x的时间或者持续区间。观测到隔离装置s8无动作,假设正常情况下门应该在1 000 ms处开始动作,但车门并未动作,电机自动保护停止转动。求取可能发生故障的运行设备。
3.3.1 诊断模型的构造
图5为采用TC-CPN模型正向构造的车门EDCU控制的扩展时间自控Petri网模型,将该模型和上述算例作为算法1的输入,对构造的TC-CPN进行求逆,得到诊断模型如图5所示,各元素整理如下:
(1)S={s1,s2,s3,s4,s5,s6,s7,s8,s9,s10,s11,s12};
(2)T={t1,t2,t3,t4,t5};
(3)F如图5所示;
(4)I={(s8,t3)};
(5)τ(t1)=[80,100],τ(t2)=[600,650],τ(t3)=[700,750],τ(t4)=[10,20],τ(t5)=0;
(6)W(t1,s3)=W(s9,t3)=S1,W(t4,s9)=S6,其余弧的权值默认为1;
(7)M0={(s1,{(1,[110,800],{})}),(s2,{(0,[800,800],{})}),(s3,{(ε,[ϖ,ϖ],{})}),(s4,{(0,[228,228],{})}),(s5,{(ε,[ϖ,ϖ],{})}),(s6,{(1,[850,1 000],{})}),(s7,{(0,[170,170],{})}),(s8,{(ε,[ϖ,ϖ],{})}),(s9,{(ε,[ϖ,ϖ],{})}),(s10,{(-1,[1 000,1 000],{})}),(s11,{(ε,[ϖ,ϖ],{})}),(s12,{(ε,[ϖ,ϖ],{})})}。
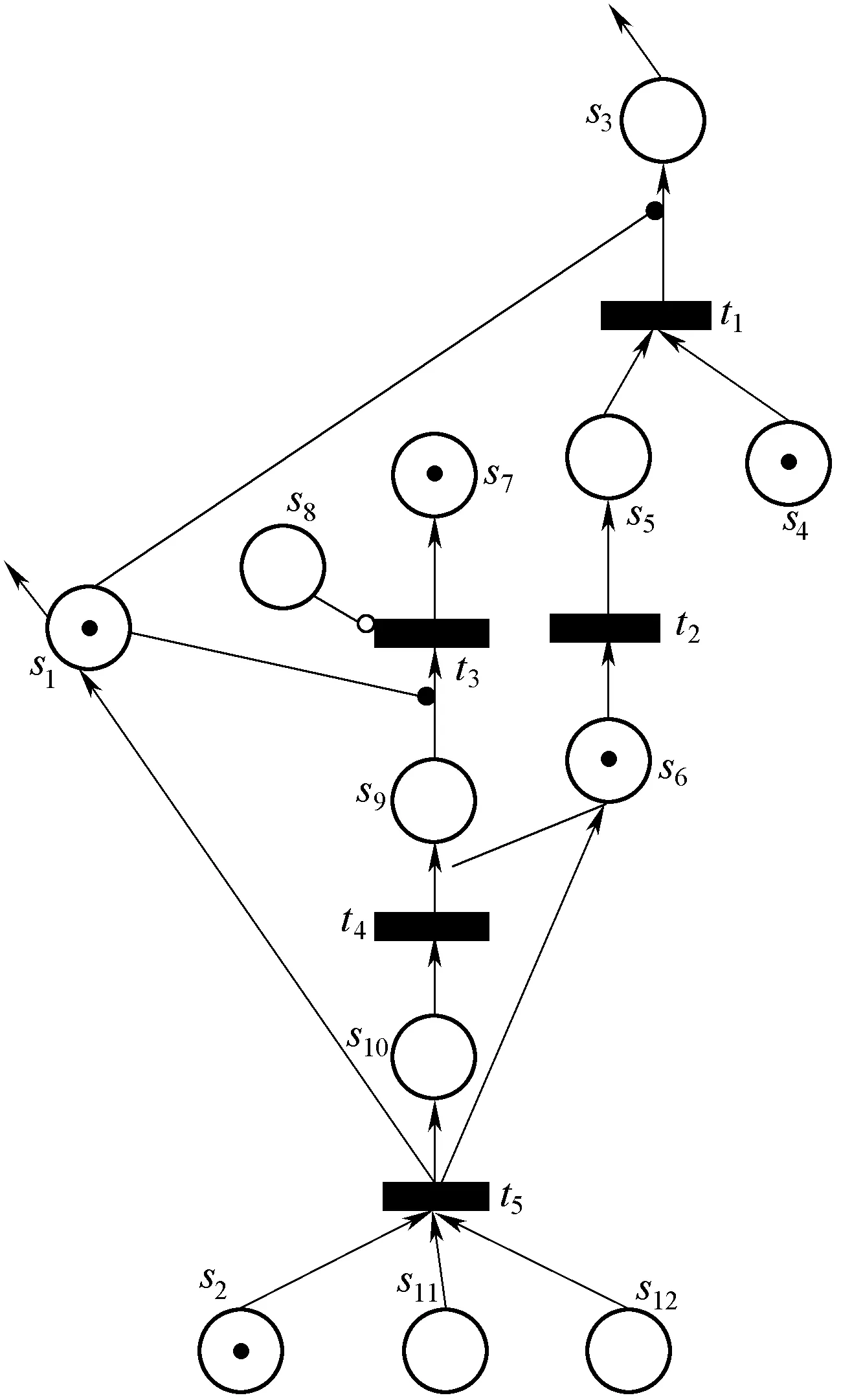
图5 EDCU控制开门动作开始的诊断模型
3.3.2 溯因故障诊断过程
运行TC-CPN模型进行溯因推理,分别计算如下:
(1)W(t4,s9)=s6且O(s6)=[850,1 000],则t4有发生权M0[t4>M1:
M1={(s1,{(1,[110,800],{})}),(s2,{(0,[800,800],{})}),(s3,{(ε,[ϖ,ϖ],{})}),(s4,{(0,[228,228],{})}),(s5,{(ε,[ϖ,ϖ],{})}),(s6,{(1,[850,1 000],{})}),(s7,{(0,[170,170],{})}),(s8,{(ε,[ϖ,ϖ],{})}),(s9,{(-1,[980,990],{s10=-1})}),(s10,{(-1,[1 000,1 000],{})}),(s11,{(ε,[ϖ,ϖ],{})}),(s12,{(ε,[ϖ,ϖ],{})})}。
(2)M1[t3>M2:
M2={(s1,{(1,[110,800],{}),(-1,[980,990],{s10=-1})}),(s2,{(0,[800,800],{})}),(s3,{(ε,[ϖ,ϖ],{})}),(s4,{(0,[228,228],{})}),(s5,{(ε,[ϖ,ϖ],{})}),(s6,{(1,[850,1 000],{})}),(s7,{(0,[170,170],{}),(-1,[230,290],{s9=-1})}),(s8,{(ε,[ϖ,ϖ],{})}),(s9,{(-1,[980,990],{s10=-1})}),(s10,{(-1,[1 000,1 000],{})}),(s11,{(ε,[ϖ,ϖ],{})}),(s12,{(ε,[ϖ,ϖ],{})})}。
(3)M2[t2>M3:
M3={(s1,{(1,[110,800],{}),(-1,[980,990],{s10=-1})}),(s2,{(0,[800,800],{})}),(s3,{(ε,[ϖ,ϖ],{})}),(s4,{(0,[228,228],{})}),(s5,{(0,[200,250],{s6=1})}),(s6,{(1,[850,1 000],{})}),(s7,{(0,[170,170],{}),(-1,[230,290],{s9=-1})}),(s8,{(ε,[ϖ,ϖ],{})}),(s9,{(-1,[980,990],{s10=-1})}),(s10,{(-1,[1 000,1 000],{})}),(s11,{(ε,[ϖ,ϖ],{})}),(s12,{(ε,[ϖ,ϖ],{})})}。
(4)M3[t3>M4:
M4={(s1,{(1,[110,800],{}),(-1,[980,990],{s10=-1})}),(s2,{(0,[800,800],{})}),(s3,{(0,[128,148],{s4=1}),(0,[100,170],{s6=1,s5=0})}),(s4,{(0,[228,228],{})}),(s5,{(0,[200,250],{s6=1})}),(s6,{(1,[850,1 000],{})}),(s7,{(0,[170,170],{}),(-1,[230,290],{})}),(s8,{(ε,[ϖ,ϖ],{})}),(s9,{(-1,[980,990],{s10=-1})}),(s10,{(-1,[1 000,1 000],{})}),(s11,{(ε,[ϖ,ϖ],{})}),(s12,{(ε,[ϖ,ϖ],{})})}。
3.3.3 诊断结果分析
为使溯因故障诊断过程计算结果更清晰,将库所的令牌变化整理简化,见表2。说明M0为监控捕获的初始状态,表2每行分别表示经上述计算过程,每触发一个变迁后汇入各库所的令牌状态。

表2 库所的令牌汇入
分析诊断结果:
(1)观测到隔离装置s8无动作,假设门正常情况下应该在1 000 ms处开始动作,在库所s10置入令牌-1,[1 000,1 000]。M0(s11)=ε,M0(s12)=ε,M0(s2)=0,变迁t5没有发生权,分析s2可能存在误动,没有实现同步。
(2)值得注意的是,s1的观测实际区间与推理区间不符,由W(s9,t3)=s1,分析弧(s9,t3)在区间[980,990]不符合权值要求,未能向s9传递托肯,即EDCU过早转入下一状态,导致允许车门动作的信号未能正确发出,以致车门未能在正常时间内开始动作。
(3)注意到O(s7)=170表示最早捕获到s7的时间与溯因推理得到的时间区间[230,290]不一致,经分析可知,s7状态只要满足在290 ms时刻之前由系统内传感器探测得到,就不会影响后续开门动作在合理时间内发生。
(4)根据定义3和定义4计算得到s3可能发生的两个区间[128,148]与[100,170],依据定义令牌一致性判定可知两区间具有一致性,两者互相映证可推测s3正常。此外,O(s1)=[110,800]表示s1被捕获的最早时刻110 ms同时满足早于两个区间的最晚时刻,推测在此阶段s1正常。
根据分析结果判断EDCU过早的从状态s1即电气控制发出开门信号的阶段,转入状态s2即控制机械装置开门的阶段,使得允许车门动作的控制信号没有正确发出,车门未在规定时间内开始动作。
4 相关对比分析
对上述算例采用带抑止弧的一般Petri网进行建模如图6所示。不难看出,为正确描述EDCU以及电机正常运转对整个模型的控制作用,模型中出现多处环路以实现交互控制。
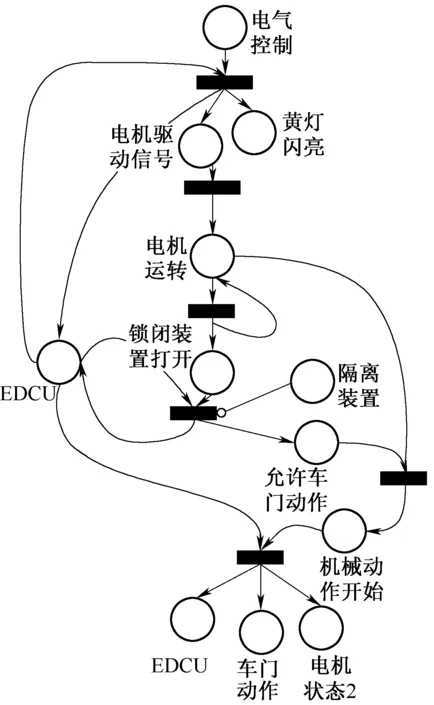
图6 带抑止弧的一般Petri网模型
自控网系统CPN与一般Petri网系统的区别在于它的变迁可以有可变权,且可变权与网系统的动态行为有关。由于自控系统的非线性关系,其有更强的描述能力,使得建模时模型具有较低的复杂度。表3将TC-CPN模型与一般petri网PN、自控petri网CPN以及时间-概率Petri网TPPN[13]进行了相关的对比分析。
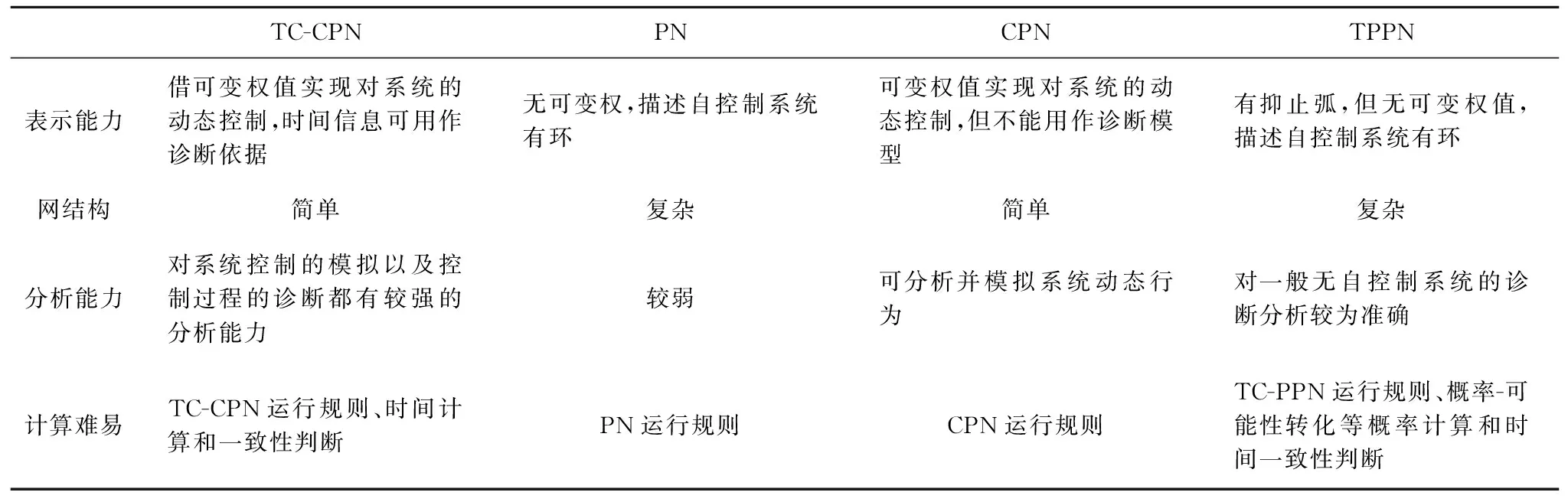
表3 相关对比分析
由表3可以得出如下结论:
(1)本文提出使用带抑止弧自控Petri网建模(如图4),采用弧的可变权表示控制关系,对比图6既保证了托肯保持的要求,在逻辑上更加符合实际,例如EDCU在发挥控制作用期间一直保持得电,又消除了模型中的闭合环路,与一般Petri网相比有较低的复杂度。
(2)时间信息是自控系统行为的重要属性,直接影响系统的状态转移,本文在自控网基础上融合了时间约束,为正确诊断故障源提供了时间维度的证据。
5 结束语
本文采用时间约束自控Petri网对城轨列车的核心控制部分进行建模分析,设计了一种通过时间计算和溯因推理,根据捕获信息的时序一致性分析诊断系统可能存在的故障源或隐患的方法。本文提出的时间约束自控Petri网模型可以推广用于解决交互控制系统的计算机模拟和故障诊断问题,如面向资源流和任务流并行业务过程的建模以及故障诊断;也可用于对强调物理世界与信息世界深度融合与交互作用的信息物理融合系统CPS(Cyber-Physical System)的建模和诊断。算例分析表明,该建模方法对此类型的控制系统具有较好的语义描述能力,与无自控能力的一般Petri网相比有较低的复杂度。此外,在模型中融入时间因素做逆向溯因推理,为查找故障隐患提供了有力的证据。
将此模型扩展到信息物理融合系统CPS的建模和诊断问题将是下一阶段的主要工作。
参考文献:
[1]POOLE D. Explanation and Prediction: An Architecture for Default and Abductive Reasoning[J]. Computational Intelligence, 1993, 5(2): 97-110.
[2]CHAKRABORTY S, KONAR A, JAIN L C. An Efficient Algorithm to Computing Max-min Inverse Fuzzy Relation for Abductive Reasoning[J]. IEEE Transactions on Systems, Man, and Cybernetics Part A:Systems and Humans, 2010, 40(1): 158-169.
[3]ROMDHANE L B, AYEB B. An Evolutionary Algorithm for Abductive Reasoning[J]. Journal of Experimental and Theoretical Artificial Intelligence, 2011, 23(4): 529-544.
[4]VANDERHAEGEN F, CAULIER P. A Multi-viewpoint System to Support Abductive Reasoning[J]. Information Sciences, 2011, 181(24): 5 349-5 363.
[5]BISTARELLI S, MARTINELLI F, SANTINI F. A Semiring-based Framework for the Deduction/Abduction Reasoning in Access Control with Weighted Credentials[J]. Computers and Mathematics with Applications, 2012, 64(4): 447-462.
[6]NAN C, EUSGELD I, KROGER W. Analyzing Vulnerabilities between SCADA System and SUC Due to Interdependencies[J]. Reliability Engineering and System Safety, 2013, 113(1): 76-93.
[7]叶阳东, 程少芬, 王旭, 等. 基于一种混合Petri 网的列车运行系统的建模与分析[J]. 铁道学报, 2009, 31(5):42-49.
YE Yangdong,CHENG Shaofen,WANG Xu, et al. Modeling and Analyzing of Train Operation Systems Based on a Kind of Hybrid Petri Net[J]. Journal of the China Railway Society, 2009, 31(5):42-49.
[8]佘维, 叶阳东. 一种基于贝叶斯Petri网的故障诊断方法 [J]. 小型微型计算机系统, 2011, 32(11):2 303-2 308.
SHE Wei,YE Yangdong.Power System Fault Diagnosis Method Based on Bayesian Petri Nets[J].Journal of Chinese Computer Systems, 2011, 32(11):2 303-2 308.
[9]LUO X,MLADEN K. Implementing Fuzzy Reasoning Petri-nets for Fault Section Estimation[J]. IEEE Trans on Power Delivery,2008,23(2):676-685.
[10]FUSS H E. AFMG-Ein Asynchroner Fluss-Modell-Generator[R]. Gesellschaft für Mathematik und Datenverarbeitung, 1975.
[11]YUAN C Y. S-and T-Invariants in Cyber Net System[J]. Journal of Computer Science & Technology, 1995,10(3):239-252.
[12]林闯,刘婷,曲扬.一种不确定时段的扩展时段时序逻辑:时间Petri网模型表示和线性推理[J].计算机学报,2001,24(12):1 299-1 309.
LIN Chuang,LIU Ting,QU Yang.Extended Interval Temporal Logic for Undetermined Interval:Model ing and Linear Inference Using Time Petri Nets[J]. Chinese Journal of Computers,2001,24(12):1 299-1 309.
[13]佘维,宋伟,叶阳东. 因果链解耦的时间—概率模型[J]. 计算机集成制造系统, 2013,19(10):2 536-2 549.
SHE Wei,SONG Wei,YE Yangdong.Time-probability Model for Causal Chains Decoupling[J].Computer Integrated Manufacturing System, 2013,19(10):2 536-2 549.

