基于备选列车接续的周期性列车运行图编制模型研究

郭根材，聂 磊，佟 璐，贺振欢

(1.北京交通大学 交通运输学院，北京 100044；2.中国铁道科学研究院 电子计算技术研究所，北京 100081)

为提高换乘客流服务质量周期性列车运行图模型[1-5]明确规定了列车接续约束。国内一些学者对周期性列车运行图的研究以单条线路为主[6-10]，列车接续约束设置简单或被忽略，研究侧重于模型求解算法、计算机编制周期性列车运行图等方面。欧洲铁路经过多年运营，已经形成固定的列车接续关系，编制周期性列车运行图的列车接续约束是明确的[11，12]；而我国高速铁路快速成网，列车运行图随新线的开通不断调整，尚未形成明确的列车接续关系。编制周期性列车运行图时，列车接续可能与运行图的安全间隔约束矛盾，列车接续需要根据实际情况调整，根据周期性列车开行方案生成的列车接续[14]仍为备选列车接续。

编图过程中，列车开行方案、备选列车接续、列车运行图三者相互制约，需要不断根据运行线间的冲突调整列车开行方案、列车接续方案，以保证运营阶段列车安全运行。本文侧重研究周期性列车开行方案给定时基于备选列车接续的周期性列车运行图编制模型，以提高周期性列车运行图在我国高速铁路的适用性。介绍欧洲铁路使用的周期性列车运行图编制模型(Cycle Periodicity Formulation，CPF模型)；针对固定列车接续，研究备选列车接续条件下CPF模型求解周期性列车运行图存在的问题，提出基于备选列车接续的周期性列车运行图编制流程；给出新流程中分类整数圈基的构造方法，改进CPF模型的整数圈基约束条件以避免CPF模型重构；进一步调整CPF模型的决策变量、目标函数与约束条件，建立适合备选列车接续的周期性列车运行图编制模型PCCPF模型；以我国高速铁路网为例，运用Cplex12.3对模型求解，进行了案例验证。

1 CPF模型

运用CPF模型编制周期性列车运行图的核心思想是将列车事件(到达、出发、通过)的发生时刻看作周期势，列车事件的发生间隔看作周期压[2，3]，利用列车事件间的约束关系构建表示列车到发间隔约束的有向图(称为约束图)，进而根据约束图中圈的周期性质构建周期性列车运行图编制模型。约束图G=(N，A)的顶点N代表列车事件，约束图的边A代表列车事件间的约束关系，如列车发发间隔约束、到发间隔约束等。约束图的每条边a∈A存在一个取值范围la≤xa≤ua表示列车事件之间应满足的约束条件，xa为边a的周期压，la为最小发生间隔，ua为最大发生间隔。约束图的边A由运行边Ar、停站边Ad、安全边As、接续边Ac等组成。图1为区段AD之间两列列车构成的约束图，图中每条边上的数值区间[la，ua]表示列车事件之间应满足的约束条件，如图中点1与点7之间的弧表示两列车在A站的出发间隔约束，弧上数值区间[4，56]表示两列车在A站的出发间隔应在4～56 min之内，以满足4 min安全追踪间隔要求，约束图的详细介绍可参考文献[13]。

图1 两列列车的约束图

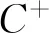
( 1 )

aC≤qC≤bC∀C∈G

( 2 )

( 3 )

( 4 )

文献[3]进一步证明，如果约束图G的整数圈基满足圈周期约束( 1 )，则约束图G中所有的圈都满足圈周期约束，CPF模型中的圈周期约束( 1 )可以简化为式( 5 )。整数圈基B是指图G线性圈空间V的r个线性无关的圈向量，如果线性圈空间V中的每一个圈向量γG都可以由整数线性表示，则称为图G的一个整数圈基。如图1中的虚线圈为约束图的一个整数圈基。本文将圈基中的圈称为基圈。

( 5 )

经过多年的发展，CPF模型已经运用于荷兰铁路[3]和柏林地铁[4]的周期性列车运行图编制中，CPF模型的详细介绍可参考文献[3]和文献[7]。CPF模型结构如下

( 6 )

s.t.

∀C∈B

( 7 )

la≤xa≤ua∀a∈A

( 8 )

aC≤qC≤bC∀C∈B

( 9 )

xa∈Z∀a∈A

(10)

qC∈Z∀C∈B

(11)

2 基于备选列车接续周期性列车运行图编制流程

相对固定列车接续，备选列车接续条件下编制周期性列车运行图需要根据运行图编制的实际情况不断迭代调整列车接续，而调整列车接续时，CPF模型会产生以下问题：

(1)描述CPF模型的约束图随列车接续的调整动态变化

调整列车接续时，约束图的接续边Ac会发生变化，导致约束图的拓扑结构改变，从而改变了约束图的整数圈基B；由整数圈基构成的约束条件( 5 )也需做相应的调整，导致备选列车接接续条件下CPF模型在求解过程中需要不断重构。固定列车接续、备选接续条件下，运用CPF模型编制周期性列车运行图的流程分别如图2(a)与图2(b)所示。

(2)换乘客流的接续服务在列车接续调整过程中缺乏保障

固定列车接续条件下编制周期性列车运行图，提供接续服务的换乘客流OD不变，换乘客流的接续服务在运行图编制过程中可以得到保障；备选列车接续条件下编制周期性运行图，不同的列车接续组合服务的换乘客流OD不同，导致调整列车接续时换乘客流的列车接续服务缺乏保障。调整列车接续不仅影响列车接续直接服务的一次换乘客流，而且影响多个列车接续接力服务的多次换乘客流。

(3)周期性列车运行图的稳定性随列车接续的调整动态变化

列车接续是影响周期性列车运行图稳定性重要因素，在实际运营阶段根据列车的晚点程度维持或取消列车接续，维持列车接续往往造成严重的晚点传播，取消列车接续又会降低换乘客流服务质量，所以调整列车接续时还应兼顾不同组合的列车接续对周期性列车运行图的稳定性。

图2 固定列车接续与备选列车接续的周期性列车运行图编制流程比较

本文通过分类整数圈基使列车接续边形成的基圈与其他基圈保持独立，避免了求解列车接续时传统CPF模型的重构；通过调整传统CPF模型的决策变量与目标函数，保证换乘客流的列车接续服务，从而确定了备选列车接续条件下周期性列车运行图编制的新流程(图2(c))。由于运行图稳定性不仅与列车接续有关，还与冗余时间设置有关，为简化模型本文暂不考虑列车接续与周期性列车运行图稳定性的作用关系。

3 适应备选列车接续的分类整数圈基

如果将约束图的整数基圈按照是否包含接续边分类，并使包含接续边的基圈保持相互独立，调整列车接续时只需松弛调整列车接续对应的基圈，而不需要调整其他基圈，避免了约束图整数圈基的重复搜索。本文将具有上述特征的整数圈基称为“分类整数圈基”。

分类整数圈基由两类基圈构成：一类基圈B1由运行边、停站边、安全边组成，不包含列车接续边；另一类基圈B2由列车接续边、运行边、停站边、安全边组成，且每个基圈只包含一个列车接续边，B1∪B2构成约束图的一个整数圈基。第二类基圈与备选列车接续具有一一对应关系，记作：{c⊃C|C∈B2，c∈Ac}。

在第二类基圈的圈周期约束( 5 )中添加松弛变量μC∈Ζ用于判断对应的备选列车接续的选定状态，当μC=0时接续基圈未被松弛，对应的备选列车接续被选定；第二类基圈的圈周期约束( 5 )转变为式(12)

∀C∈B2

(12)

4 基于分类整数圈基的周期性列车运行图编制模型

4.1 决策变量

决策变量xa∈Ζ表示约束图G边a∈A的周期压；决策变量yc={0，1|c∈Ac}表示备选列车接续c是否为被选定。

多次换乘客流OD需要多个列车接续接力服务，调整列车接续不仅影响列车接续直接服务的一次换乘客流OD，还影响其间接服务的多次换乘客流OD。引入“二次列车接续”的概念，一个二次列车接续(c1，c2)由两个列车接续{c1∈Ac，c2∈Ac}组成，服务两次换乘客流。由于三次及以上换乘客流较小，本文暂不考虑。决策变量z(c1，c2)表示二次接续(c1，c2)是否形成。z(c1，c2)与yc1、yc2存在耦合关系，只有备选列车接续c1、c2同时被选定时二次接续(c1，c2)才能形成，即

z(c1，c2)与yc1、yc2的耦合关系可用式(13)表示。

2z(c1，c2)≤yc1+yc2≤2z(c1，c2)+1
∀c1，c2∈Ac

(13)

4.2 目标函数

周期性列车运行图编制目标可以设为旅客总旅行时间最小、列车总运行时间最小、动车组运用数量最少、运行图稳定性最强等多类目标。由于本文重点研究基于备选列车接续的周期性列车运行图编制问题，模型目标选取列车总运行时间最小、列车接续服务换乘客流最大。

(1)列车总运行时间最小。列车运行总时间最小不仅可以减少旅客的旅行时间，而且可以减少动车组的运用时间。

(14)

(2)列车接续服务换乘客流最大。列车接续服务的换乘客流越多，越有利于提高换乘客流的服务质量。fc为备选列车接续c∈Ac服务的一次换乘客流量；f(c1，c2)为二次列车接续(c1，c2)服务的两次换乘客流量。

(15)

增加目标权重系数ψ，将多目标规划转换为单目标规划，模型目标函数转换为

(16)

4.3 约束条件

(1)圈周期性质约束。根据分类整数圈基构建圈周期约束，式(17)为第一类基圈的圈周期约束，式(18)为第二类基圈的圈周期约束。

(17)

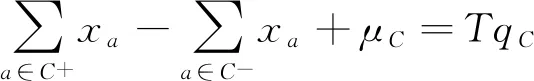
(18)

决策变量yc与第二类基圈的松弛变量μC存在耦合关系，如果基圈C对应备选列车接续c，则

yc与μC的耦合关系可表示为式(19)，其中M为一个极大数。

-M(1-yc)≤μC≤M(1-yc)
∀C∈B2，c∈Ac且c⊃C

(19)

(2)圈变量约束。圈变量qc取值范围根据式( 3 )、式( 4 )计算。

aC≤qC≤bC∀C∈B1∪B2

(20)

(3)接续对称约束。我国列车基本成对开行，列车接续关系也应具有对称性。列车接续需满足对称约束(21)，其中c′为备选列车接续c的对向备选列车接续。

yc=yc′∀c∈GC

(21)

(4)运行图约束。运行图约束是保证列车安全运营的重要约束，由列车区间运行时间约束、停站时间约束、安全间隔约束、接续时间约束等组成，代表了列车到达、通过、出发等事件应满足的间隔时间，这些约束可归纳为式(22)。各类约束的取值范围计算方法文献[4]已经作了详细介绍，本文不再重复。

la≤xa≤ua∀a∈A

(22)

综上所述，建立基于列车接续备选集的周期性列车运行图编制模型(Potential Connections & Cyclic Timetabling Model，PCCTM)为

s.t.

∀C∈B1

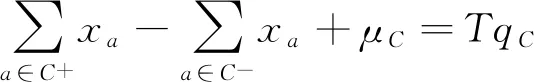
aC≤qC≤bC∀C∈B1∪B2

-M(1-yc)≤μC≤M(1-yc)

∀C∈B2，c∈Ac且c⊃C

2z(c1，c2)≤yc1+yc2≤2z(c1，c2)+1 ∀c1，c2∈Ac

yc=yc′∀c∈Ac

la≤xa≤ua∀a∈A

xa∈Z∀a∈A

yc，z(c1，c2)∈[0，1] ∀c，c1，c2∈Ac

5 案例分析

选取速度等级为300 km/h及部分速度等级为200 km/h的线路作为案例路网，涉及26个节点城市，31个车站，29个区段，路网规模约8 700 km(见图3)。周期性列车开行方案的周期长度为1 h，周期列车仅考虑大节点停站的高速列车，共计32对/h(见表1)，为增加列车停站组合数量，每类列车的开行频率设为1列/h。周期性列车开行方案服务542个客流OD，其中290个直达客流OD、152个一次换乘客流OD、100个二次换乘客流OD。列车运行速度300km/h等级线路取270 km/h，200 km/h等级线路取180 km/h；起停车附加时分300 km/h等级线路分别取2 min、3 min，200 km/h等级线路分别取2 min、2 min，追踪间隔时间取4 min；列车停站时间取2～8 min，列车接续时间取15～25 min；案例考虑的备选一次列车接续有58个，备选二次列车接续有36个，表2为案例使用的部分备选一次列车接续。

图3 高速铁路路网图

编号列车起讫点编号列车起讫点编号列车起讫点1G1北京—哈尔滨西23G23深圳北—南昌西45G45武汉—济南西2G2哈尔滨西—北京24G24南昌西—深圳北46G46济南西—武汉3G3北京—大连25G25哈尔滨西—大连47G47西安北—广州南4G4大连—北京26G26大连—哈尔滨西48G48广州南—西安北5G5北京—吉林27G27吉林—大连49G49西安北—杭州东6G6吉林—北京28G28大连—吉林50G50杭州东—西安北7G7北京—沈阳北29G29上海虹桥—广州南51G51沈阳北—郑州东8G8沈阳北—北京30G30广州南—上海虹桥52G52郑州东—沈阳北9G9北京南—上海虹桥31G31上海虹桥—武汉53G53哈尔滨西—吉林10G10上海虹桥—北京南32G32武汉—上海虹桥54G54吉林—哈尔滨西11G11北京南—杭州东33G33上海虹桥—西安北55G55沈阳北—上海虹桥12G12杭州东—北京南34G34西安北—上海虹桥56G56上海虹桥—沈阳北13G13北京南—合肥35G35上海虹桥—青岛57G57哈尔滨西—天津西14G14合肥—北京南36G36青岛—上海虹桥58G58天津西—哈尔滨西15G15北京南—青岛37G37上海虹桥—天津西59G59大连—天津西16G16青岛—北京南38G38天津西—上海虹桥60G60天津西—大连17G17北京西—太原南39G39上海虹桥—长沙南61G61北京西—南昌西18G18太原南—北京西40G40长沙南—上海虹桥62G62南昌西—北京西19G19北京西—西安北41G41深圳北—武汉63G63济南西—西安北20G20西安北—北京西42G42武汉—深圳北64G64西安北—济南西21G21北京西—深圳北43G43广州南—太原南22G22深圳北—北京西44G44太原南—广州南

表2 备选列车接续方案

根据周期性列车开行方案和备选列车接续构建约束图，约束图包含612个点、1 824条边。设置目标权重系数ψ为-1，运用CPLEX 12.3对模型进行求解。运算环境为Win7-64位操作系统，12G内存，Core i7四核处理器，求解获得42个列车接续、18个二次列车接续，占备选列车接续的72.4%，占备选二次列车接续的50%。最终选定的列车接续能够服务的一次换乘客流OD有132个，二次换乘客流OD有52个，共184个，占换乘客流OD数量的73%、换乘客流量的85.8%，求解获得的列车接续见表3。案例开行列车的总运行时间为22 460 min，总运行距离为79 900 km，平均旅速为213.4 km/h，平均列车接续时间为19.4 min，图4显示了列车在沿途节点车站的时刻信息，图中方框表示列车途经车站，方框上的数字表示列车在该站的到达时刻与出发时刻。

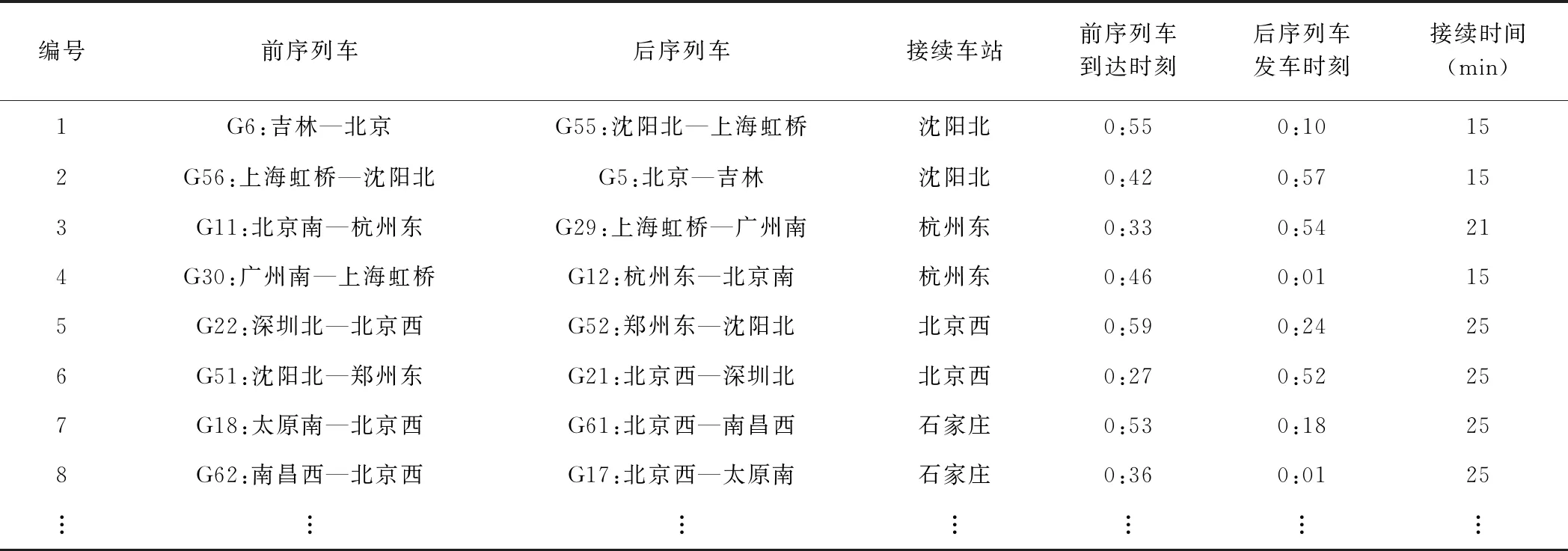
表3 求解获得的列车接续

6 结论

根据周期性列车开行方案设计的列车接续关系需要在周期性列车运行图编制阶段根据运行图编制状态选定，研究案例从58个备选列车接续中选出了42个列车接续，占备选列车接续的72.4%；设计的分类整数圈基有效避免了调整列车接续时传统CPF模型的重构；从案例求解结果可以看出73%的换乘OD、85.8%的换乘客流提供了换乘时间在15～25 min之间的接续服务，表明PCCPF模型具有较好的适用性。

PCCPF模型解决了备选列车接续条件下周期性列车运行图的编制问题，既可以保证换乘客流的列车接续服务又可以满足周期性列车运行图的编制要求，提高了周期性列车运行图在我国的适用性。接续稳定性是影响列车接续服务性能的重要因素，影响列车接续可靠性的因素不仅有列车接续类型，如始发终到接续、中间站接续，还有区间冗余时间的设置，可对列车接续稳定性问题开展进一步研究。

参考文献：

[1]NACHTIGALL K.Periodic Network Optimization and Fixed Interval Timetables[D].Hildesheim:University Hildesheim,1998.

[2]ODIJK M.Railway Timetable Generation[D].Delft: Delft University of Technology,1997.

[3]PEETERS L.Cyclic Railway Timetable Optimization[D].Rotterdam:Erasmus University Rotterdam,2003.

[4]LIEBCHEN C.The First Optimized Railway Timetable in Practice[J].Transportation Science,2008,42(4):420-435.

[5]KROON L.Flexible Connections in PES PModels for Cyclic Passenger Railway Timetabling[J].Transportation Science,2014,48(1):136-154.

图4 高速铁路网周期性列车运行图

[6]汪波,杨浩,牛丰,等.周期运行图编制模型与算法研究[J].铁道学报,2007,29(5):1-6.

WANG Bo,YANG Hao,NIU Feng,et al.Study on Model and Algorithm of Periodic Train Diagram Generation[J].Journal of the China Railway Society,2007,29(5):1-6.

[7]汪波,韩宝明,战明辉,等.城市轨道交通网络周期运行图编制研究[J].铁道学报,2013,35(4):9-15.

WANG Bo,HAN Baoming,ZHAN Minghui,et al.Study on Formulation of Periodic Train Diagram of Urban Rail Transit Network[J].Journal of the China Railway Society,2013,35(4):9-15.

[8]谢美全,聂磊.周期性列车运行图编制模型研究[J].铁道学报,2009,31(4):7-13.

XIE Meiquan,NIE Lei.Model of Cyclic Train Timetable[J].Journal of the China Railway Society,2009,31(4):7-13.

[9]聂磊,张渊,武鑫.计算机编制周期性列车运行图关键技术[J].中国铁道科学,2014,35(1):114-121.

NIE Lei,ZHANG Yuan,WU Xin.Key Technologies for Computer Generation of Cyclic Train Timetable[J].China Railway Science,2014,35(1):114-121.

[10]贾晓秋.客运专线旅客列车周期运行图的优化理论与方法研究[D].成都:西南交通大学,2011.

[11]郭根材,聂磊.基于欧洲列车时刻表的高速铁路列车衔接方案探讨[J].北京交通大学学报,2012,36(6):21-26.

GUO Gencai,NIE Lei.Train Connection Plan for High-Speed Railway Based on European Rail Timetable[J].Journal of Beijing Jiaotong University,2012,36(6):21-26.

[12]付慧伶,聂磊,杨浩.基于欧洲列车时刻表的高速列车行车组织方案[J].北京交通大学学报,2009,33(3):45-51.

FU Huiling,NIE Lei,YANG Hao.Operation Plan for High-Speed Train Based on European Rail Timetable[J].Journal of Beijing Jiaotong University,2009,33(3):45-51.

[13]LIEBCHEN C,PEETERS L.Integral Cycle Bases for Cyclic Timetabling[J].Discrete Optimization,2009,6(1):98-109

[14]郭根材,聂磊,佟璐.高速铁路网周期性列车运行图接续约束生成模型[J].铁道学报,2015,37(8):1-7.

GUO Gencai,NIE Lei,TONG Lu.Train Connection Model for Cyclic Timetable of High Speed Rail Network[J].Journal of the China Railway Society,2015,37(8):1-7.