铁路风速单步高精度混合预测性能对比研究

刘 辉，田红旗，李燕飞，张 雷

(1.中南大学 轨道交通安全教育部重点实验室，湖南 长沙 410075；2.德国Rostock大学 信息科学与电子工程学院，德国 罗斯托克 18109)

恶劣强风是造成铁路行车事故的主要自然灾害之一[1，2]。为应对该灾害，国内外学者在设计铁路挡风墙[3-5]、列车气动外形优化[6-9]、强风列车倾覆稳定性建模[1，10-12]、气动数值计算[13-16]等方面开展了大量的研究工作。此外，近年来国际上开始致力于研建一种新型的铁路强风实时监控与主动预警系统。如德国国家铁路公司的Nowcasting System大风监测预警系统[17]，东日本铁路公司的Windas System大风列车预警系统[18]以及我国自主开发的兰新、青藏等强风线路的大风监测与预警系统[19]。这类系统均根据强风铁路沿线测风站的实测风速融合列车和线路实现行车指挥。虽然这种基于实测风速的模式目前也能用于指挥行车，但当强风消失后，铁路部门由于无法预知该位置点的未来风速变化趋势，出于安全考虑，不得不对受控列车继续保持一段时间的“限速”或“停轮”状态，降低了运输效率[17-19]。如果这类大风监测预警系统具备风速预测功能，则可按如图1所示的框架开展工作。即作为铁路调度指挥系统TDCS的辅助系统，以列车行车计划(包括车次、时间和到站)为主线，融合铁路路况信息(如桥梁、隧道、大弯曲半径等)和风速倾覆稳定性，计算获得不同风速等级的列车安全行车速度。同时，预警系统实时保持对沿线实测风速的单步预测计算，当发现某列车的前方将出现超等级的危险大风时，可以提前向列车发出“限速”或“停轮”命令。反之，系统通过预测发现某大风将消失，则可以发出相应的“恢复”命令。当然，这涉及到系统集成、实时通信、数据融合与决策、行车优化、风速预测等众多问题。本文重点研究铁路风速的高精度瞬时单步预测问题。

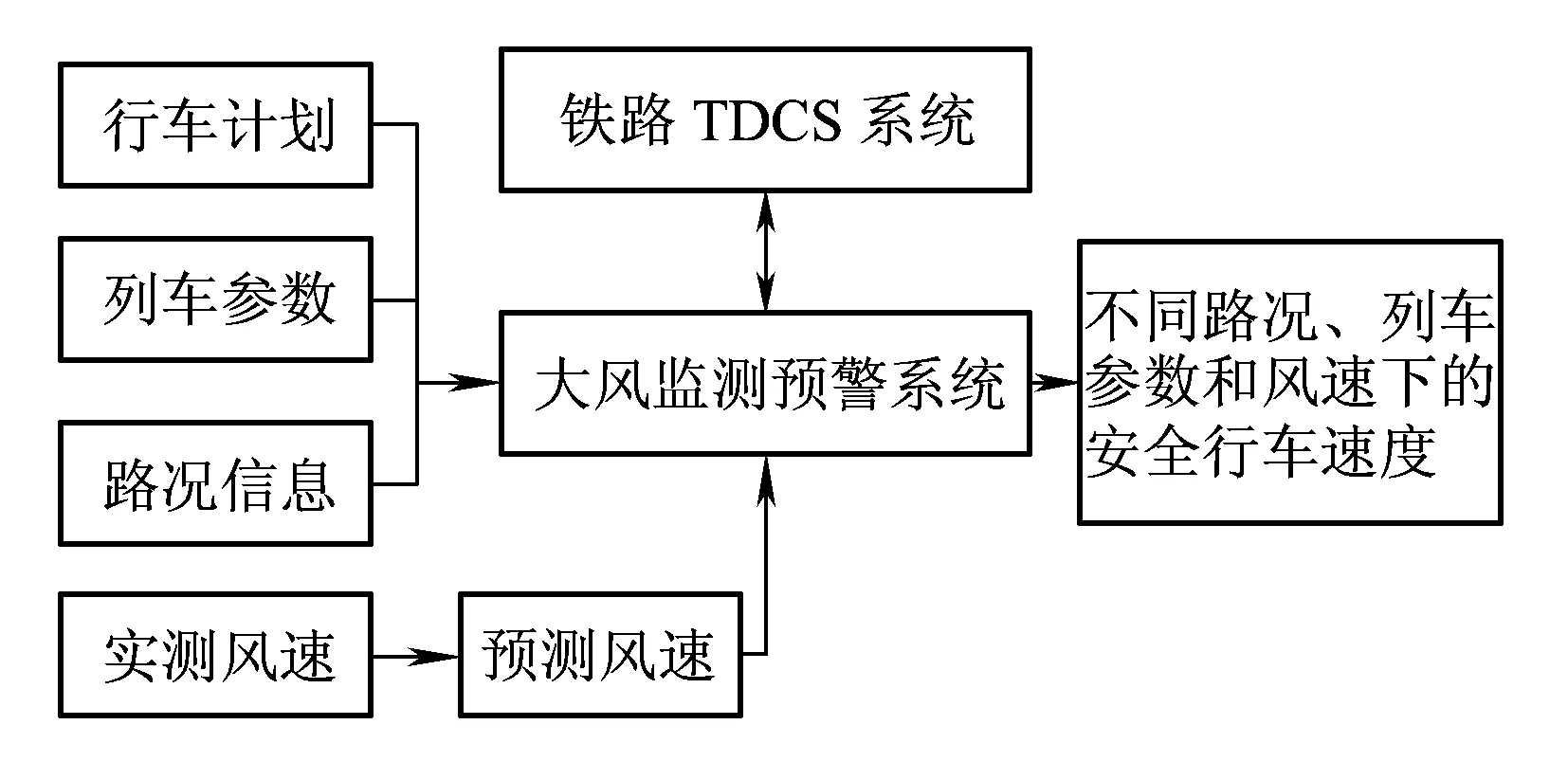
图1 融合预测风速的大风监测预警系统结构图

实际上，铁路风速的高精度预测已成为国内外争先解决的核心技术之一。文献[17]提出基于线性外推理论的铁路风速短期预测方法。文献[18]提出基于卡尔曼滤波理论的铁路风速预测方法。文献[20-22]开展了铁路沿线风速短期预测研究。在信号处理领域，小波分解理论被称为“数学显微镜”，能够将任何一种非平稳信号转化为一组较为平稳信号[23]。在人工智能领域，神经网络是信号非线性处理的优秀代表[24]。因此，本文拟采用这两种优秀理论取长补短所形成的两种不同混合算法(小波-神经网络法和小波型神经网络法)预测铁路沿线的非平稳风速信号，并对其预测结果进行对比分析。

1 铁路原始风速序列

本文运用混合预测算法对我国青藏铁路沿线3处监控点的实测大风风速序列{X1(t)}、{X2(t)}和{X3(t)}进行建模与预测。每处监控点拥有400个采样数据，所有采样间隔均为3 min。取原始序列的前300个数据建立预测模型，后100个数据用于检验模型。3组原始风速序列如图2～图4所示。

图2 原始风速序列{X1(t)}

图3 原始风速序列{X2(t)}

图4 原始风速序列{X3(t)}

2 小波-神经网络法预测铁路风速

2.1 建模原理

小波-神经网络法的建模流程如图5所示，包括如下步骤：

(1)选择小波法对拟预测铁路风速序列进行多层分解与重构计算，将原始非平稳风速序列转化为多层较平稳风速序列，以减低后期分解层上建立高精度神经网络预测模型的难度。在本步骤中，为了确定最优的小波分解参数，选择对小波母函数和小波分解深度的不同组合进行预测性能比较。

(2)利用神经网络法对各小波分解层分别建立合适的预测模型。并用所建的神经网络模型对各分解层风速序列进行超前单步预测计算。在本步骤中，为了选择最优的神经网络建模参数，利用时序ARIMA模型辅助确定神经网络的结构，同时对6种主流的神经网络学习算法进行性能筛选。主流学习算法包括带动量的梯度下降算法、自适应LR动量梯度下降算法、弹性梯度下降算法、Fletcher-Reeves共轭梯度算法、量化共轭梯度算法和拟牛顿算法。

(3)对获得的各层风速预测值进行加权计算，输出原始序列的预测值。

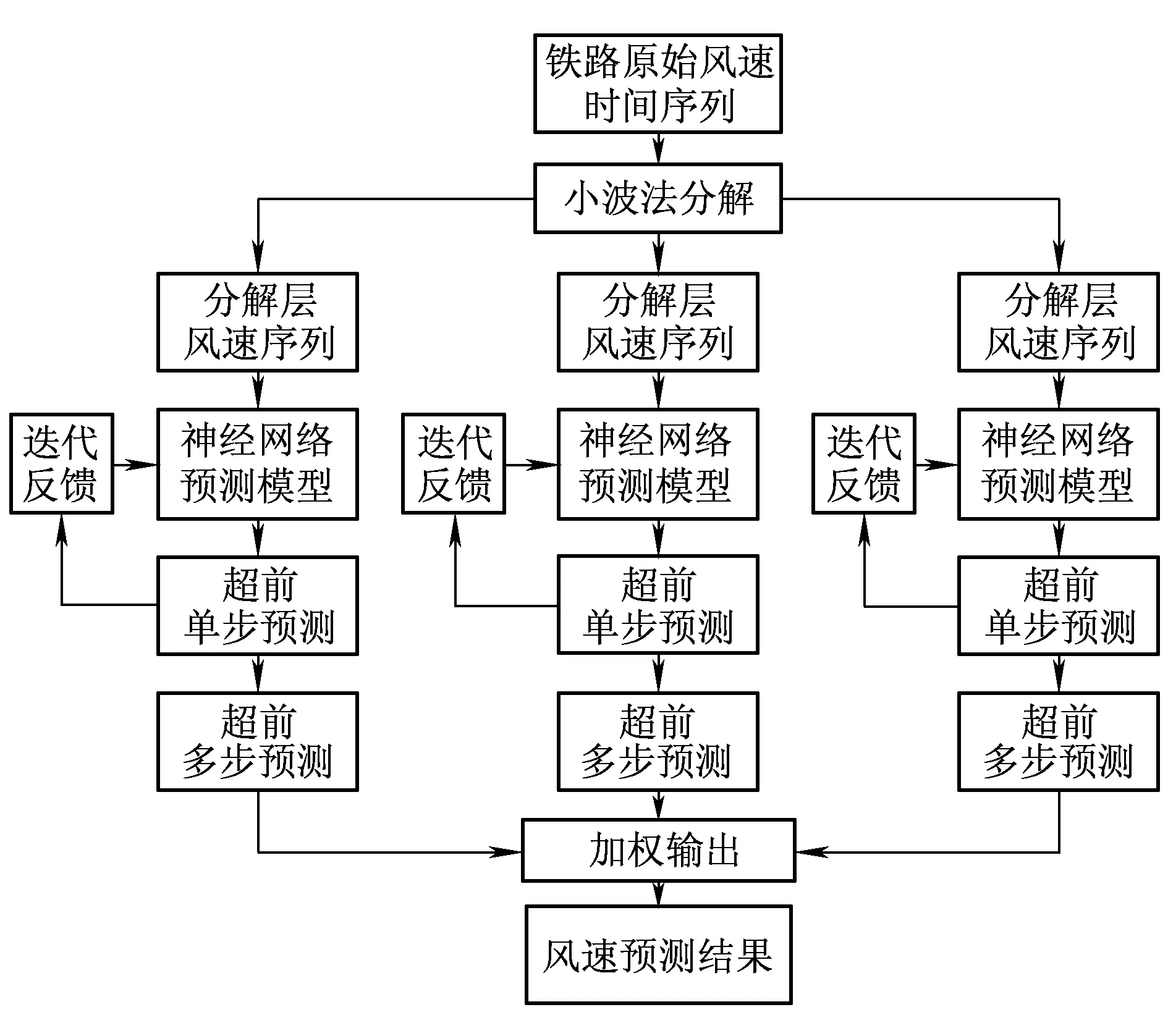
图5 小波-神经网络法的建模和预测流程图

2.2 计算步骤

2.2.1不同的小波分解参数对小波-神经网络法模型的预测性能影响

小波分解是将原始信号分解成一些呈现相对平稳性的分解层数据的叠加[23]。从数学上解释，小波分解是将基本小波函数φ(t)平移τ后，在不同尺度a下与待分析的原始信号x(t)做内积，即

( 1 )

本文运用小波法分解铁路沿线非平稳风速序列的计算流程，如图6所示。每进行一次小波分解称为一个分解深度。

为研究不同小波母函数和小波分解深度对小波-神经网络模型预测性能的影响，选择在小波法理论中最具代表性的三类母函数(Daubechies 函数、Haar函数和Symlets函数)和两种深度工况(3层和6层)的共计6种不同参数组合对图2所示的铁路原始风速数据进行小波分解与重构计算。例如，Haar小波与3个分解深度的组合计算结果如图7所示。对各个小波分解结果数据分别建立BP神经网络模型并进行试预测计算，再利用式( 2 )～式( 4 )的精度评价指标对试预测结果进行对比分析，最终筛选出最优的铁路风速小波分解参数组合。试预测的检验样本为原始风速序列{X1(t)}的前300个数据。

图6 三个分解深度的小波法计算流程

图7 小波法分解结果示例

平均绝对误差(MAE)

( 2 )

平均相对误差(MPE)

( 3 )

均方根误差(RMSE)

( 4 )

6种不同小波分解参数组合的预测评价结果见表1。为便于区分，将这6种不同组合分别命名为：H3(Haar小波+3层分解)、H6(Haar小波+6个分解深度)、D3(Daubechies小波+3个分解深度)、D6(Daubechies小波+6个分解深度)、S3(Symlets小波+3个分解深度)和S6(Symlets小波+6个分解深度)。

表1 不同小波分解参数的试预测结果分析

通过分析表1可知：

(1)对同一个小波母函数而言，增加分解深度并没有提高后期神经网络模型的试预测精度。以Haar小波函数为例，其6层分解的平均相对误差比3层分解的对应指标仅提高6.10%。但由于6层分解比3层分解多产生接近50%的分解层数据，因此6层分解在小波分解计算和神经网络模型训练方面将多花费接近50%的时间。

(2)对同一个分解深度而言，Symlets小波函数获得最好的精度指标，之后依次是Daubechies 小波函数和Haar小波函数。

(3)综上，本文最终选择“Symlets函数+3个分解深度”用于铁路风速预测。

2.2.2不同的神经网络学习算法对小波-神经网络混合模型的预测性能影响

如图5所示，小波-神经网络法除了需要确定合适的小波分解参数之外，还需要对每个分解层建立最优的神经网络预测模型。在对分解层建立神经网络模型方面，参考文献[2]提出了基于时间序列模型辅助确定神经网络结构参数的做法，即先对各个分解层的数据建立时序ARIMA模型，然后将获得的ARIMA差分方程的自变量认定为神经网络的输入节点，将其因变量认定为神经网络的输出节点，最后运用尝试法迭代筛选出最优的神经网络隐含层节点数。这种利用时间序列模型优化神经网络模型的做法能够有效避免网络参数选定的随机性和人为性，提高所建网络的非线性拟合精度。

除了神经元数量，神经网络模型对学习算法也很敏感。但在文献[2]中没有这部分内容。本文将补充开展这方面的工作。本文用图2所示原始风速序列{X1(t)}的前400个采样点作为实验样本，对6种主流的神经网络学习算法进行分类考核，其结果如图8和表2所示。

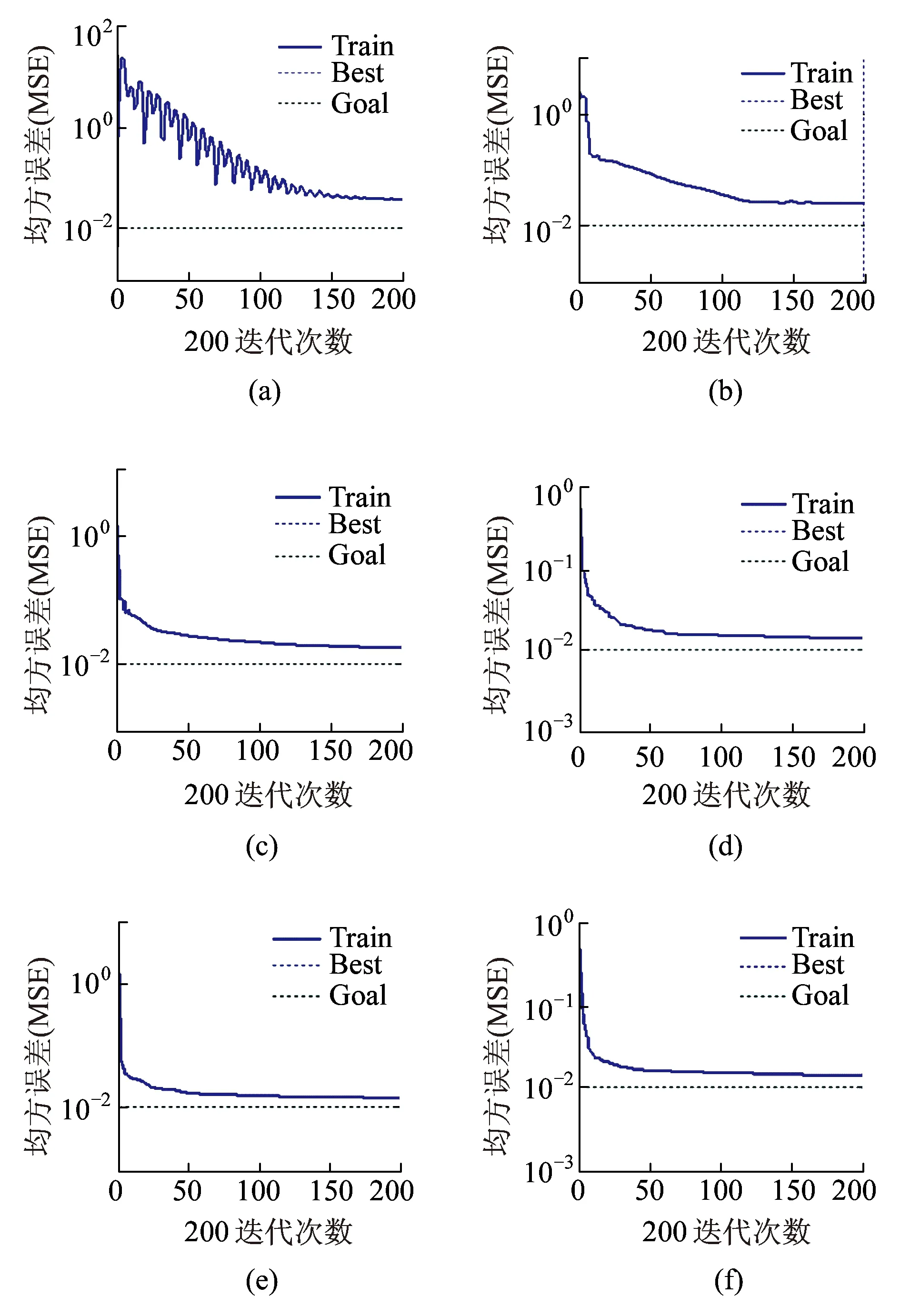
图8 不同神经网络学习算法的拟合结果

学习算法指标σ1/(m·s-1)σ2/%σ3/(m·s-1)带动量的梯度下降算法1.748813.932.2170自适应LR动量梯度下降算法1.06738.811.3416弹性梯度下降算法0.87448.281.1389Fletcher-Reeves共轭梯度算法0.91988.291.0481量化共轭梯度算法0.84096.471.0447拟牛顿算法0.34682.710.4525

分析图8和表2可知：在相同的铁路风速学习样本和条件下，拟牛顿算法获得了最优的学习效果，其拟合的平均相对误差仅为2.71%，远高于其他的网络学习算法。因此，本文最终选择拟牛顿算法用于风速预测计算。

3 小波型神经网络法预测铁路风速

小波型神经网络是以前馈型神经网络拓扑结构为基础，将小波基函数作为隐含层节点的传递函数，遵循误差方向传播的神经网络模型[24]。如图9所示，小波基取代其他传统函数(如Sigmoid函数)作为隐含层节点的传递函数，图中，Ni是输入神经元个数，Nj是隐含层小波基神经元个数，Nk是输出神经元个数。

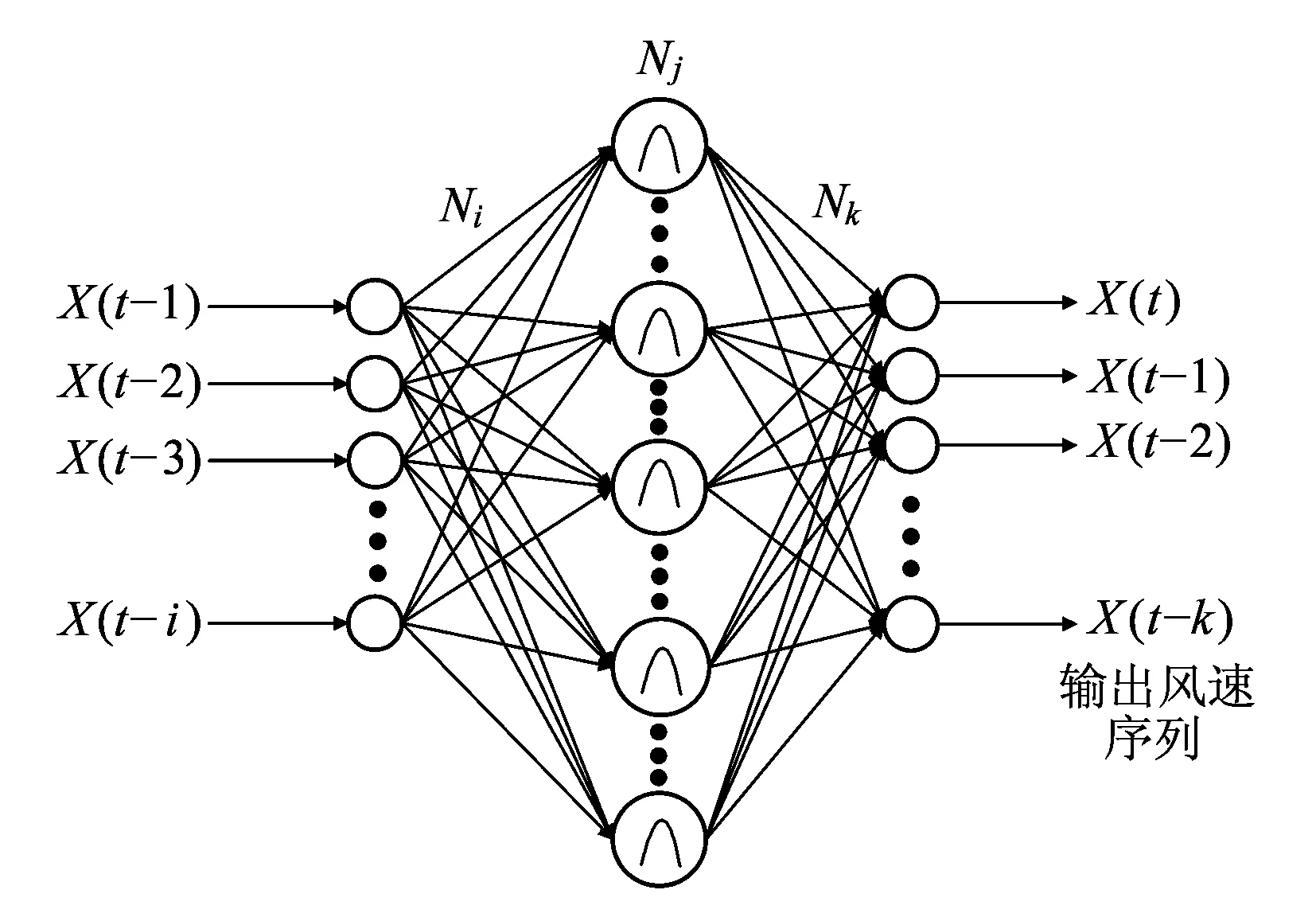
图9 小波型神经网络结构

根据如图9所示的小波型神经网络模型结构，当输入风速序列为{xi}时，网络的隐含层输出为

( 5 )

式中：h(j)为隐含层第j个节点输出值；ωij为输入层和隐含层的连接权值；hj为小波基母函数；τj为小波基函数hj的平移因子；aj为小波基函数hj的伸缩因子；Ni为输入层节点数。

小波神经网络输出层的计算公式为

( 6 )

式中：y(k)为输出层的输出值；ωjk为隐含层和输出层的连接权值；h(j)为第j个隐含层节点的输出；Nj为隐含层节点数；Nk为输出层节点数。

本文采取梯度下降算法作为小波型神经网络模型的嵌入学习算法，具体计算公式如下。

(1)计算网络预测误差

( 7 )

(2)修正小波型神经网络权值和小波基函数系数

( 8 )

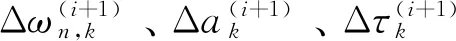
( 9 )

小波型神经网络模型也根据时序ARIMA模型确定网络的输出-输出节点结构。小波型神经网络模型将按照如图10所示的计算框架完成铁路风速超前预测计算。

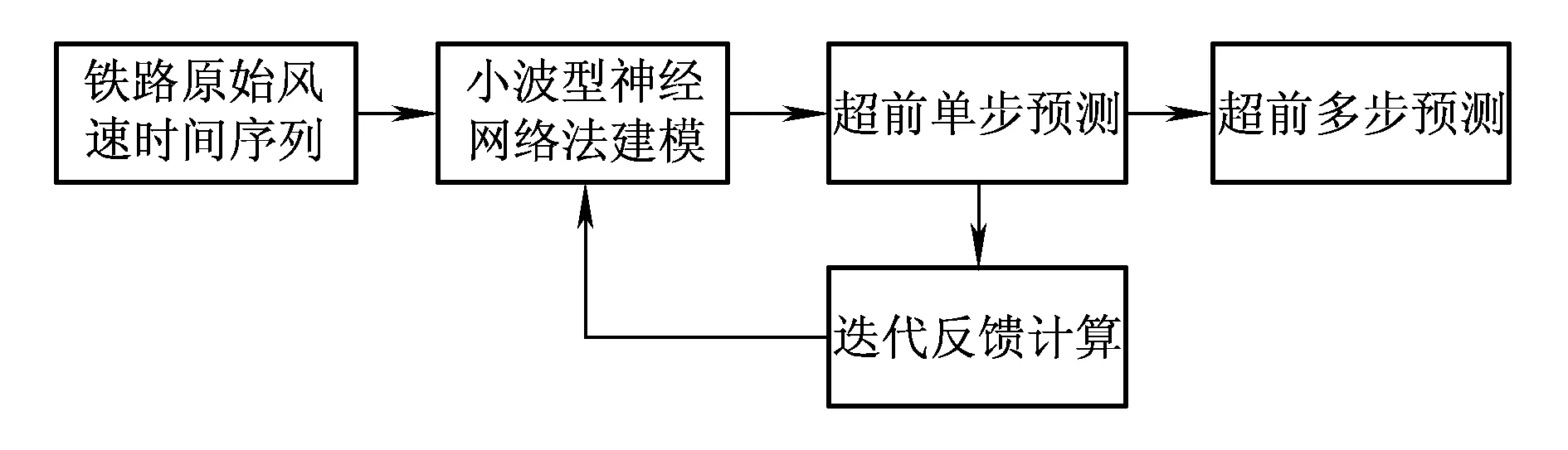
图10 小波型神经网络模型的预测流程

4 预测结果分析与比较

为充分比较小波型神经网络法和小波-神经网络法两种不同算法的预测性能，本文分别用小波型神经网络模型、小波-神经网络模型和单种BP神经网络模型对如图2～图4所示的3组铁路原始风速数据进行超前多步预测计算。在预测过程中，将建模数据和预测数据分开，即用风速序列的前300个数据建立预测模型，后100个数据检验模型。

(1)小波型神经网络模型对不同测风站风速的预测结果

小波型神经网络混合模型对3组铁路原始风速序列的预测结果如图11～图13所示。利用式( 2 )～式( 4 )预测精度评价指标评估所获得的预测值结果见表3。

图11 {X1(t)}序列的小波型神经网络预测结果

图12 {X2(t)}序列的小波型神经网络预测结果

图13 {X3(t)}序列的小波型神经网络预测结果

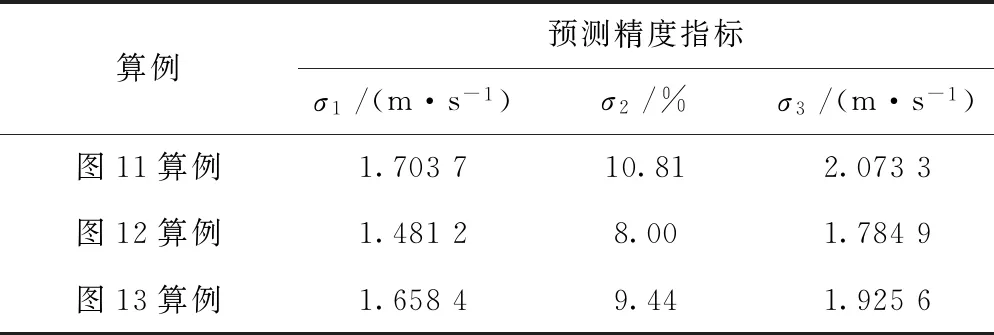
算例预测精度指标σ1/(m·s-1)σ2/%σ3/(m·s-1)图11算例1.703710.812.0733图12算例1.48128.001.7849图13算例1.65849.441.9256

(2)小波-神经网络模型对不同测风站风速的预测结果

小波-神经网络混合模型对3组铁路原始风速序列的预测结果如图14～图16所示。其对应的预测评价指标见表4。

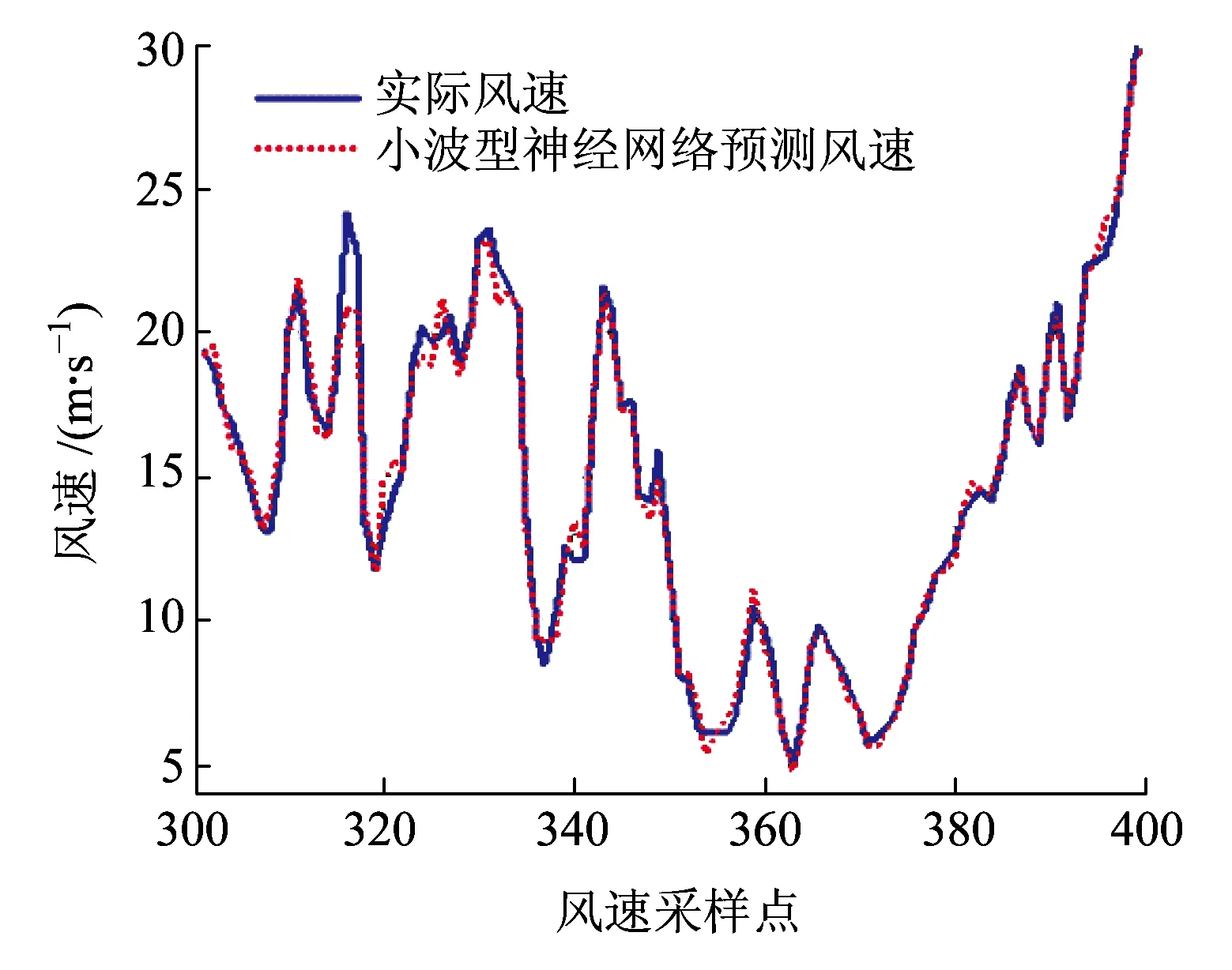
图14 {X1(t)}序列的小波-神经网络预测结果

图15 {X2(t)}序列的小波-神经网络预测结果

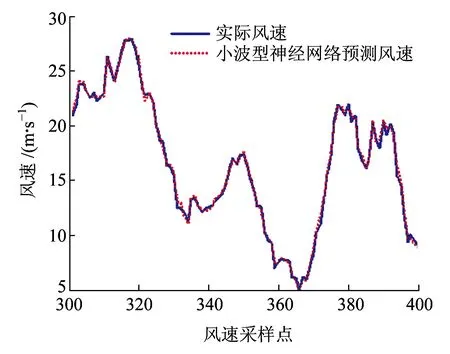
图16 {X3(t)}序列的小波-神经网络预测结果

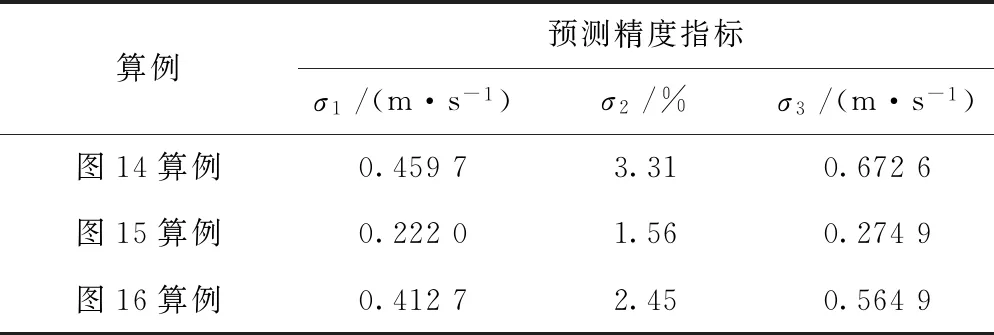
算例预测精度指标σ1/(m·s-1)σ2/%σ3/(m·s-1)图14算例0.45973.310.6726图15算例0.22201.560.2749图16算例0.41272.450.5649

(3)单种神经网络模型对不同测风站风速的预测结果

单种神经网络模型对3组铁路原始风速序列的预测结果如图17～图19所示。其对应的预测评价指标见表5。

图17 {X1(t)}序列的神经网络预测结果

图18 {X2(t)}序列的神经网络预测结果

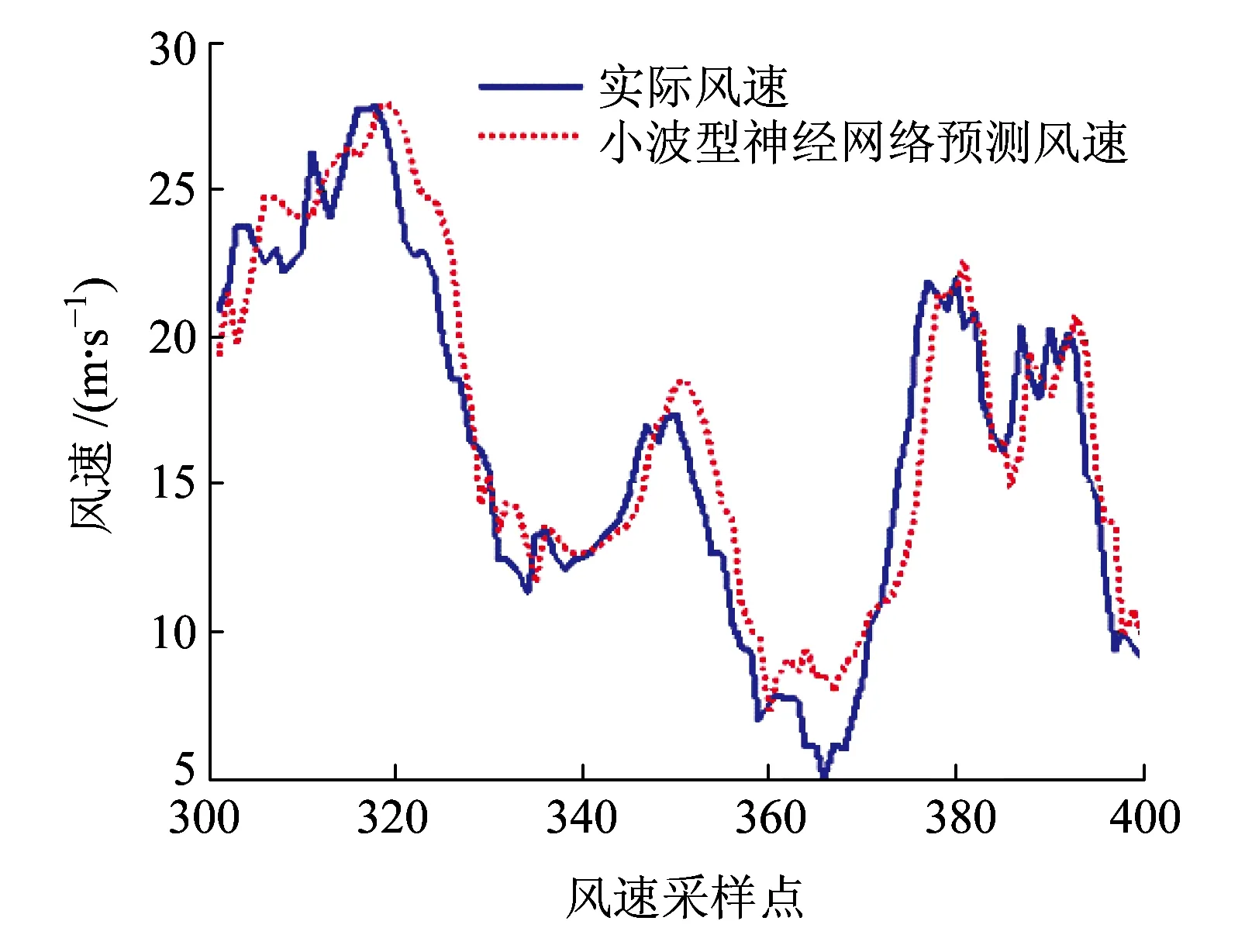
图19 {X3(t)}序列的神经网络预测结果

算例预测精度指标σ1/(m·s-1)σ2/%σ3/(m·s-1)图17算例1.778512.532.1000图18算例1.54349.951.8363图19算例1.669011.131.9668

(4)三种不同算法的性能对比

为了揭示小波分解在小波型神经网络法和小波-神经网络法两者不同混合算法中的贡献度，将两种混合算法对单种神经网络模型的性能优化百分比进行统计，见表6、表7。

通过分析表3～表5可知：小波-神经网络法的预测性能在三种预测算法中最优，然后依次是小波型神经网络法和单种神经网络法。以评价指标体系中最为重要的平均相对误差为例，在本文的3组预测实例中，小波-神经网络法的误差分别为3.31%、1.56%和2.45%，属于高精度5%的预测范畴。而小波型神经网络法的同类指标分别为10.81%、8.00%和9.44%；单种神经网络法的同类指标分别为12.53%、9.95%和11.13%。特别需要指出的是小波-神经网络法实现了对铁路瞬间突变风速数据的有效追踪。

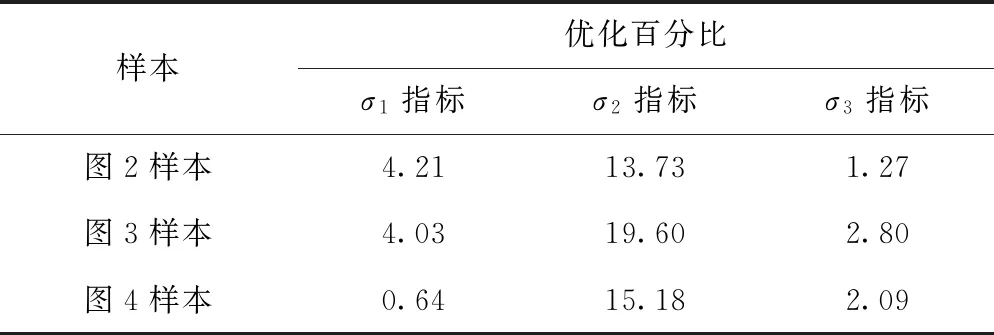
表6 小波型神经网络法提高神经网络预测精度 %

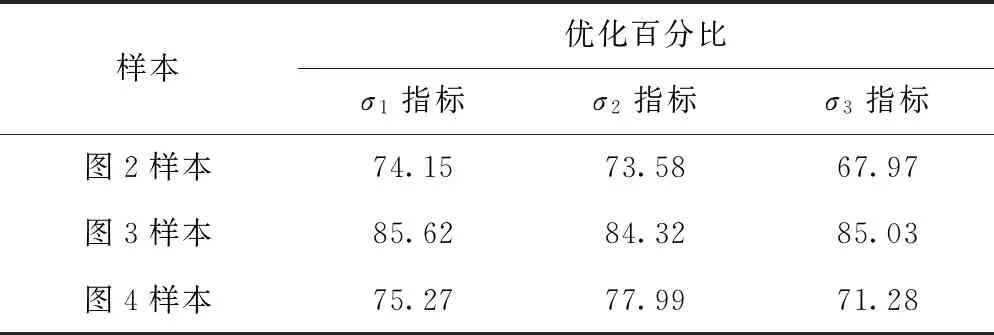
表7 小波-神经网络法提高神经网络预测精度 %

通过分析表6和表7可知，在3组不同的预测实例中，小波型神经网络混合模型对单种神经网络模型的平均相对误差优化幅度分别为13.73%、19.60%和15.18%，而小波-神经网络混合模型对单种神经网络的平均相对误差优化幅度分别为73.58%、84.32%和77.99%。后者的优化幅度远优于前者。这说明小波法用于前端分解非平稳风速所获得的贡献度高于小波法用于后期优化神经网络传递函数所获得的贡献度。究其原因，小波-神经网络法由于采用了小波法分解原始风速序列，不仅直接降低了后期神经网络模型的高精度拟合难度，而且提供了用于建立更多神经网络所需要的分解层数据。这使得小波-神经网络混合模型实现了从单个神经网络到多个神经网络群的进化，因此可以获得较为理想的预测结果。而小波型神经网络法虽然利用小波函数作为网络隐含层传递函数可以优化传统神经网络的非线性搜索性能，但究其根本它始终还是只有一个神经网络模型参与实际预测计算，因此小波传递函数所带来的优化幅度无法与小波前端分解所带来的效益相提并论。

5 结论

(1)文章的三组预测实例表明，小波-神经网络法和小波型神经网络法这两种混合算法在不同程度上都吸收了小波法的信号细分功能，具有对铁路风速跳跃点出色的辨识和分解能力。同时，两者也继承了神经网络的非线性隐射能力，能够应对铁路风速非线性变化趋势的预测要求。由于两者融合了小波分解的算法特性，因此他们都获得了比单种神经网络更加优秀的预测算法性能。但两者相比较，前者通过运用小波法分解原始风速数据从而获得了对多分解层建立多神经网络预测“群”的机会，因此达到5%的高精度预测级别。后者通过将小波函数作为网络传递函数的手段从而提高了传统单个神经网络的全局搜索性能，因此达到10%的中等精度预测级别。前者比后者获得了更好的优化性能。

(2)相对于其他算法，如时间序列分析法、单种自适应神经模糊推理法、卡尔曼滤波法等而言，虽然小波-神经网络法和小波型神经网络法这两种混合算法所包含的建模步骤更多，但通过借助MATLAB神经网络和小波分析工具箱可以方便地实现其计算步骤的编程和集成。因此他们可以在相关铁路风速预警系统中推广使用。

参考文献：

[1]高广军,田红旗,姚松,等.兰新线强横风对车辆倾覆稳定性的影响[J].铁道学报,2004,26(4):36-40.

GAO Guangjun,TIAN Hongqi,YAO Song,et al.Effect of Strong Cross-wind on the Stability of Trains Running on the Lanzhou-Xinjiang Railway Line[J].Journal of the China Railway Society,2004,26(4):36-40.

[2]刘辉,田红旗,李燕飞.基于小波分析法与神经网络法的非平稳风速信号短期预测优化算法[J].中南大学学报:自然科学版,2011,42(9):2 704-2 711.

LIU Hui,TIAN Hongqi,LI Yanfei.Short-term Forecasting Optimization Algorithm for Wind Speed from Wind Farms Based on Wavelet Analysis Method and Rolling Time Series Method[J].Journal of Central South University:Science and Technology,2011,42(9)：2 704-2 711.

[3]李田,张继业,张卫华.横风下高速列车通过挡风墙动力学性能[J].铁道学报,2012,34(7):30-35.

LI Tian,ZHANG Jiye,ZHANG Weihua.Dynamic Performance of High-speed Train Passing Windbreak in Crosswind[J].Journal of the China Railway Society,2012,34(7):30-35.

[4]李鲲.大风区高速铁路新型防风设施研究[J].中南大学学报：自然科学版,2012,43(2):756-762.

LI Kun.Research on New Anti-wind Facility of High-speed Train in Strong Wind Area[J].Journal of Central South University:Science and Technology,2012,43(2):756-762.

[5]CHU C R,CHANG C Y,HUANG C J,et al.Windbreak Protection for Road Vehicles Against Crosswind[J].Journal of Wind Engineering and Industrial Aerodynamics,2013,116(5):61-69.

[6]CHELI F,GIAPPINO S,ROSA L,et al.Experimental Study on the Aerodynamic Forces on Railway Vehicles in Presence of Turbulence[J].Journal of Wind Engineering and Industrial Aerodynamics,2013,123(6):311-316.

[7]SIMONOVIC A,SVORCAN J,STUPAR S.Aerodynamic Characteristics of High Speed Train under Turbulent Cross Winds:A Numerical Investigation Using Unsteady-RANS Method[J].FME Transactions,2014,42(1):10-18.

[8]张雷,杨明智,张辉, 等.高速铁路隧道洞门对隧道空气动力效应的影响[J].铁道学报,2013,35(11):76-79.

ZHANG Lei,YANG Mingzhi,ZHANG Hui,et al.Influence of Tunnel Portals on Tunnel Aerodynamic Effect in Operation of High-speed Railways[J].Journal of the China Railway Society,2013,35(11):76-79.

[9]WAGNER S,EHRENFRIED K,DILLMANN A.Numerical Simulation of Train-Tunnel Entry Using a BEM in Time Domain[C]//New Results in Numerical and Experimental Fluid Mechanics VIII.Berlin:Springer Berlin Heidelberg,2013:739-746.

[10]周丹,田红旗,杨明智,等.强侧风下客车在不同路况运行的气动性能比较[J].中南大学学报：自然科学版,2008,39(3):554-559.

ZHOU Dan,TIAN Hongqi,YANG Mingzhi,et al.Comparison of Aerodynamic Performance of Passenger Train Traveling on Different Railway Conditions up Strong Cross-wind[J].Journal of Central South University:Science and Technology,2008,39(3):554-559.

[11]熊小慧,梁习锋.横风作用下货车篷布结构强度计算[J].中南大学学报：自然科学版,2012,43(8):3 280-3 286.

XIONG Xiaohui,LIANG Xifeng.Numerical Simulation of Tarpaulin Structural Strength of Railway Vehicle under Cross Wind Condition[J].Journal of Central South University:Science and Technology,2012,43(8):3 280-3 286.

[12]ALLAIN E,PARADOT N.Aerodynamics in Train Cross Wind Studies[J].International Journal of Aerodynamics,2014,4(1):10-23.

[13]LI T,ZHANG J Y,ZHANG W H.Co-simulation of High-speed Train Fluid-structure Interaction Dynamics in Crosswinds[J].Journal of Vibration Engineering,2012,25(2):138-145.

[14]GILBERT T,BAKER C J,QUINN A.Gusts Caused by High-speed Trains in Confined Spaces and Tunnels[J].Journal of Wind Engineering and Industrial Aerodynamics,2013,121(5):39-48.

[15]BAKER C.A Framework for the Consideration of the Effects of Crosswinds on Trains[J].Journal of Wind Engineering and Industrial Aerodynamics,2013,123:130-142.

[16]BAKER C,CHELI F,ORELLANO A,et al.Cross-wind Effects on Road and Rail Vehicles[J].Vehicle System Dynamics,2009,47(8):983-1 022.

[17]HOPPMANN U,KOENIG S,TIELKES T,et al.A Short-term Strong Wind Prediction Model for Railway Application:Design and Verification[J].Journal of Wind Engineering and Industrial Aerodynamics,2002,90(10):1 127-1 134.

[18]KOBAYASHI N,SHIMAMURA M.Study of a Strong Wind Warning System[J].JR East Technical Review,2003(2)：61-65.

[19]贾国裕.兰新铁路大风灾害及其对策[J].路基工程,2008(2):195-197.

JIA Guoyu.Wind Hazards and Countermeasures in Lanzhou-Xinjiang Railway[J].Subgrade Engineering,2008(2):195-197.

[20]潘迪夫,刘辉,李燕飞,等.青藏铁路格拉段沿线风速短时预测方法[J].中国铁道科学,2009,30(5):129-133.

PAN Difu,LIU Hui,LI Yanfei,et al.A Short-term Forecast Method for Wind Speed Along Golmud-Lhasa Section of Qinghai-Tibet Railway[J].China Railway Science,2009,30(5):129-133.

[21]王瑞,史天运,王彤.基于RBF神经网络的铁路沿线短时风速预测方法[J].中国铁道科学,2011,32(5)：132-134.

WANG Rui,SHI Tianyun,WANG Tong.Prediction Method for Short-time Wind Speed Along Railway Based on RBF Neural Network[J].China Railway Science,2011,32(5)：132-134.

[22]苗秀娟.瞬态风荷载下的列车运行安全性研究[D].长沙:中南大学,2011:20-35.

[23]杨淑平,易国栋,袁修贵,等.一种基于分块小波的人脸识别算法[J].中南大学学报：自然科学版,2013,44(5)：1 902-1 909.

YANG Shuping,YI Guodong,YUAN Xiugui,et al.A Face Recognition Algorithm Based on Blocking Wavelet Transforms[J].Journal of Central South University:Science and Technology,2013,44(5)：1 902-1 909.

[24]史峰,王小川,郁磊,等.MATLAB神经网络30个案例分析[M].北京：北京航空航天大学出版社,2010：208-210.