以电流矢量为目标的永磁同步电机定子电流动态预测

荆 锴孙鹤旭,2董 砚郑 易

（1.河北工业大学控制科学与工程学院 天津 300130 2.河北科技大学 石家庄 050018）



以电流矢量为目标的永磁同步电机定子电流动态预测

荆 锴1孙鹤旭1,2董 砚1郑 易1

（1.河北工业大学控制科学与工程学院 天津 300130 2.河北科技大学 石家庄 050018）

摘要提出一种以电流矢量为目标的永磁同步电机（PMSM）定子电流动态预测方法。通过研究αβ静止坐标系下PMSM定子电流矢量动态响应，得出电流矢量变化的三个作用分量，并在离散周期上，利用泰勒级数对每个分量截断近似，进而得到PMSM定子电流矢量的动态预测方法。对方法中各个分量的近似误差进行了分析，同时为参数选择和应用条件提供了理论依据。最后，利用实验验证了预测方法的准确性。

关键词：永磁同步电机 电流矢量 电流预测 误差分析

河北省重大科技成果转化项目（13041709Z）和河北省自然科学基金（E2013202108）资助项目。

0 引言

永磁同步电机（Permanent Magnet Synchronous Motor,PMSM）具有高效率和高功率密度等特点，由PMSM构成的电机系统越来越多地应用在兵工和工业等领域的高性能伺服系统中。电机电磁转矩响应的快速性和稳定性是保证交流伺服系统动态性能的关键，而与电磁转矩直接相关的电流环性能则成为反映伺服系统性能的重要指标。

预测控制[1-3]具有较高的动态响应性能，能够实现快速跟踪，在定子电流跟踪的数字调节中具有较佳的性能。该方法通常是利用当前时刻的采样值和状态值，预测电流变化趋势，给出最佳的输出控制量。其中，电流变化趋势的预测过程是预测控制的关键，电流预测结果是否准确直接影响控制技术的复杂与否以及控制结果的优劣。对此，国内外学者进行了大量的研究。文献[4]分析了电流在每一个开关状态下的变化斜率，从而总结规律得到电流预测方法。文献[5]设计了前馈-反馈控制器对电流进行预测和控制。文献[6]对PMSM定子电流方程进行离散近似处理，并通过引入权重因子，得出具有鲁棒控制性能的电流方程，然而未给出反电动势的作用以及高速运行时的具体补偿措施。文献[7]结合无差拍控制思想，引入龙伯格观测器对电流进行预测。上述研究均建立在已有的预测算法上，没有对电流的动态响应进行分析，而且算法比较复杂，对反电动势所带来的电流变化分析不深入，未能全面反映电流的变化规律，预测准确度不高。此外，上述大多数研究均是基于转子磁链的dq旋转坐标，针对id、iq单独进行预测和控制，因dq电流存在耦合，一些方法致力于方程的解耦控制[8,9]，一些方法则将耦合项直接忽略[6]。这些方法是对id、iq以独立变量形式单独计算和调节的，没有将电流以矢量的形式看作整体进行预测和控制，而且dq坐标下并不能直观地反映三相电流的实际动态变化。

本文将在αβ静止坐标系下，以电流矢量为目标，将电流矢量的动态响应分解为三个独立的变化分量，根据各个分解矢量的表达式，利用泰勒级数，将连续的动态变化离散近似到控制周期上，从而得出电流矢量动态变化的预测方程。文中对近似产生的截断误差进行分析，尤其是对电机反电动势产生的电流变化矢量，给出矢量误差的轮廓线图，为相关参数的选取以及方法的应用条件等提供了理论依据。最后，通过仿真以及电机平台实验，对电流矢量的预测控制进行实际测试，得到了很好的电流预测效果。

1 PMSM模型及电流矢量的动态变化分量

PMSM在dq同步旋转坐标系中的电机“电压-电流”方程为

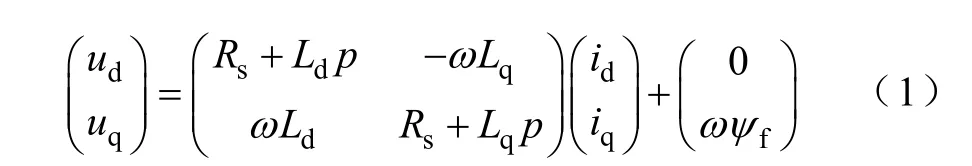
式中，Rs为定子电阻；Ld、Lq分别为d、q轴定子电感；ud、uq分别为d、q轴定子电压分量；id、iq分别为d、q轴定子电流分量；ψf为转子磁链；ω 为转子电角速度；p为微分算子。

对于隐极式PMSM，有Ld＝Lq＝Ls，利用“旋转-静止”坐标变换，令转子相对于A相轴线方向即α轴的位置为θ，则式（1）变换到αβ 坐标、并写成定子电流矢量的状态空间表达式为

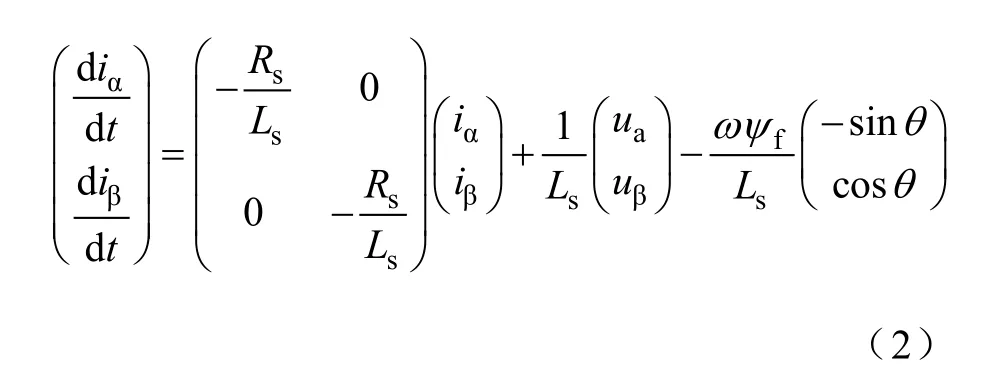
式中，iα、iβ分别为定子电流矢量is的α、β 轴电流分量；uα、uβ分别为定子电压矢量us的α、β 轴的分量。设初始时刻为t0，经过足够短的时间t，其间可认为电角速度ω 恒定，且有θ ＝θ0＋ωt，θ0为t0时刻转子的电角度；电压矢量，认为是在t时间内施加电压的平均值，其与直流母线电压Udc以及开关管状态之间的转换关系参见文献[10]。通过求解状态方程，得到电流矢量is的通解形式为

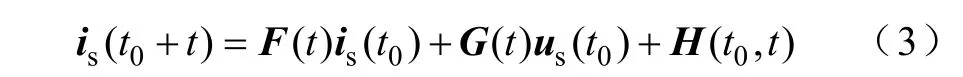
其中

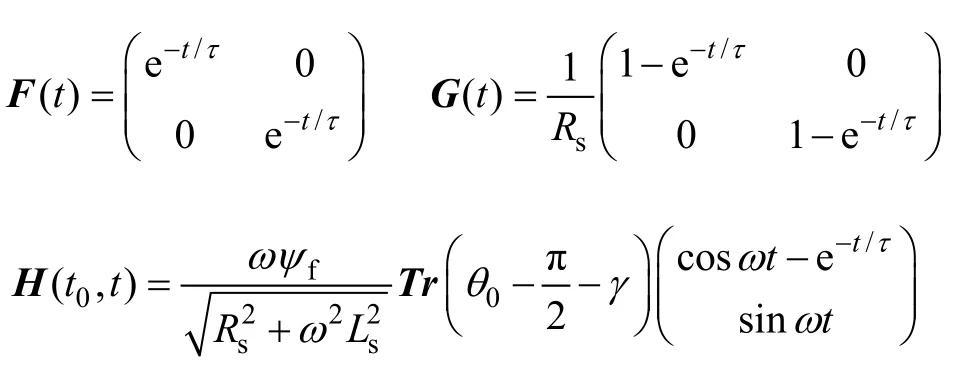
式中，τ为电机时间常数，τ＝Ls/Rs；γ＝ arctan（ωLs/Rs），是锐角；Tr（·）为逆时针旋转变换矩阵，式（3）反映了时间t内PMSM电流矢量的动态响应。如果取电流矢量变化量为

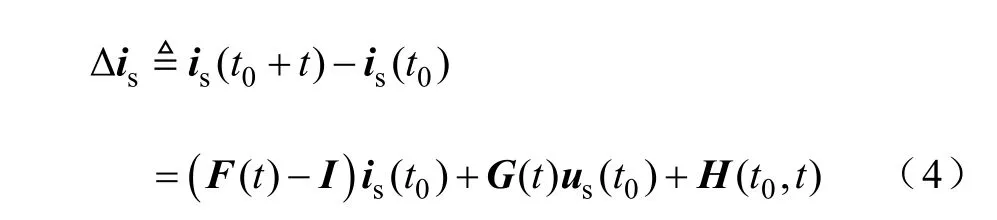
式中，引起电流矢量变化的量为初始电流矢量、输入电压矢量以及转速（反电动势矢量），三者对电流变化的作用无耦合关系，并满足电路的叠加定理，分别记为Δisi、Δisu和Δisω，则

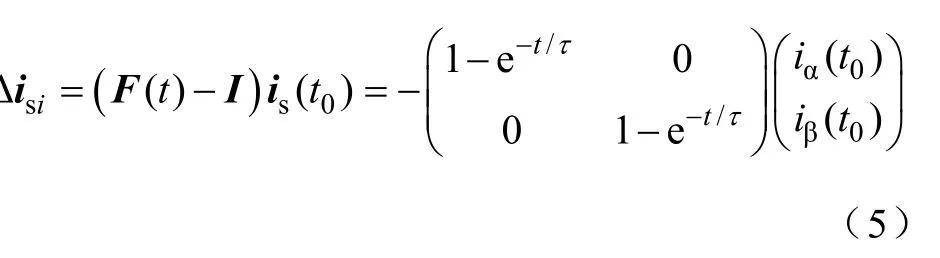
Δ

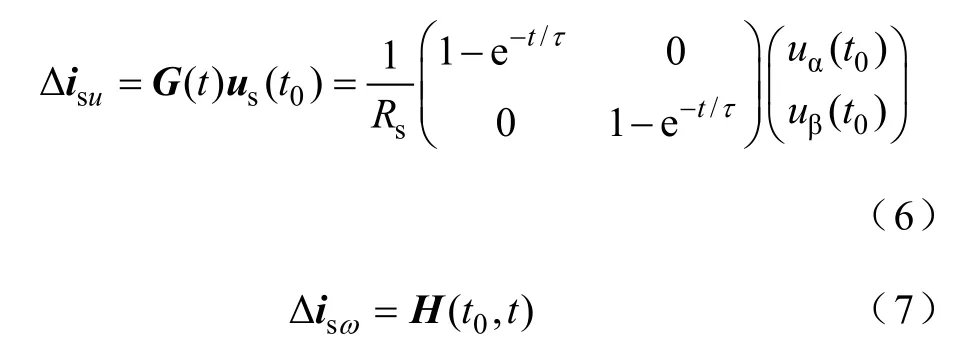
则PMSM电流变化矢量分解为三个独立的动态变化分量。三者独立作用时的响应过程分别如图1中实线和虚线所示，其中和∠Δi分别为电流矢量变化量幅值和相位。

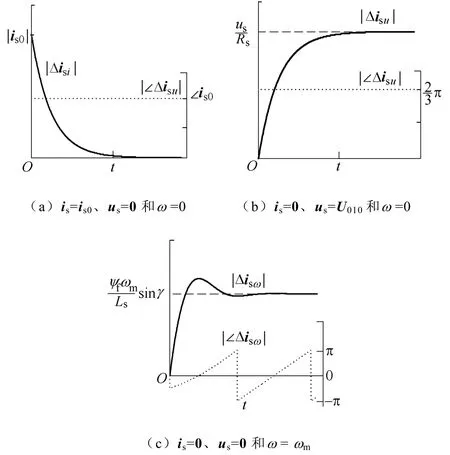
图1　电流矢量三个分量的独立响应曲线Fig.1 Response curve of the three components of current vector

由图1a可知，Δisi使电流矢量的幅值按指数规律衰减；由图1b可知，Δisu在外加电压矢量方向上使电流矢量幅值呈指数增长；由图1c可知，Δisω方向随转子位置变化，幅值形似二阶阻尼系统响应的变化，其中，低速时可近似忽略Δisω的作用，当速度较高时，分析电流矢量变化需考虑该矢量的幅值和相位的影响。

2 基于电流矢量动态响应的PMSM电流预测方法

2.1 电流矢量的动态预测

在PMSM的离散数字控制系统中，获得的电流和转速等均为离散采样值，取控制周期与采样周期同步，典型的电机电流数字控制时序为：按k-1时刻的采样值和给定值，计算当前时刻需要输出的控制量，在k时刻输出控制量，到k＋1时刻方可知道电流控制结果是否能跟随，可见，电流的跟踪延时至少为两个控制周期[11]。采用电流预测的方法，则可以减小因控制周期的延时带来的跟踪波动，在k-1时刻可以利用采样值预测k时刻的电流值，从而提前一个周期计算控制量。为实现电流跟踪的稳定，需要预测计算有较高的准确性。

基于式（4），将其分量表达式（5）～式（7）中的t替换为通常只有几十到几百微秒的采样周期Ts，表达式变为反映kTs～（k＋1）Ts一个周期内的电流变化规律，同时实现了k时刻对k＋1时刻电流值的预测计算。然而，式（5）～式（7）包含较复杂的运算，不适合数字控制器的实现，故需进行简化处理。

经离散周期Ts代换后，采用泰勒级数变化方法，将表达式展开成Ts的多项式形式，得到由k～k＋1时刻三个变化矢量和，并写成矢量的相幅表达形式。前两者为

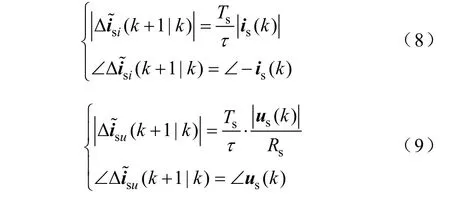
Δisω表达式较为复杂，矢量的近似处理受到电角速度ω 的影响，在低速的时候可以近似认为sinωt≈ωt、cosωt ≈1，然而速度较高时，特别是ωt接近1时，该近似不足以描述矢量。本文展开至Ts2，得到该矢量的相幅表达式为

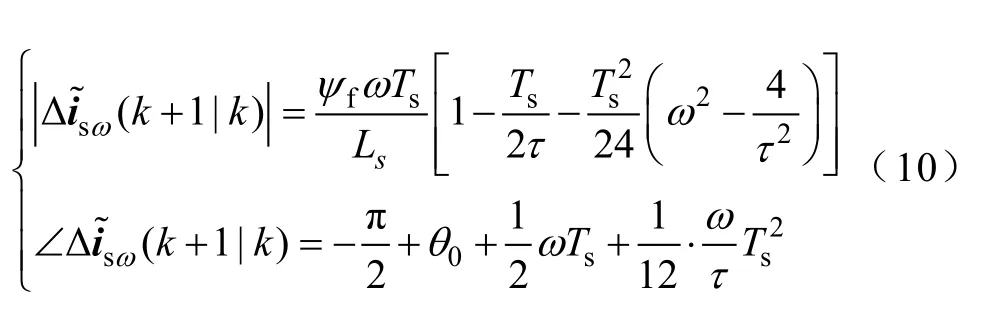
预测计算时，在误差允许范围内为减少计算量，式（10）可根据转速大小，截取至Ts的0次、1次及2次项。

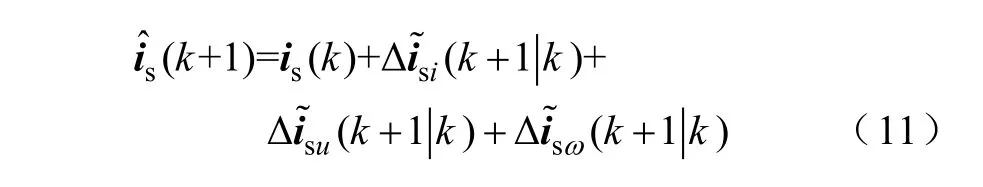
综上，电流预测矢量表达式为电机电流预测规律的αβ 坐标矢量如图2所示。

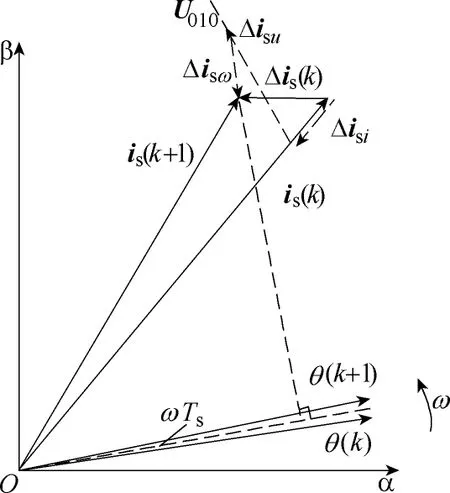
图2　电流矢量动态预测Fig.2 Current vector dynamic prediction

2.2 电流矢量动态预测的误差分析

电流矢量动态预测方法的计算过程经过了近似处理，其中存在矢量的计算误差。定义矢量的距离d和相对距离dr为

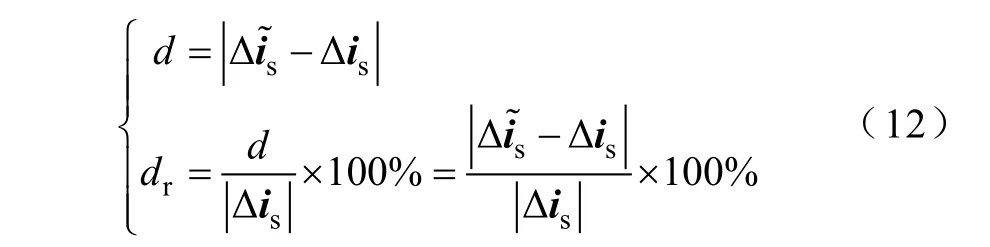
由此来作为计算误差的评价标准。

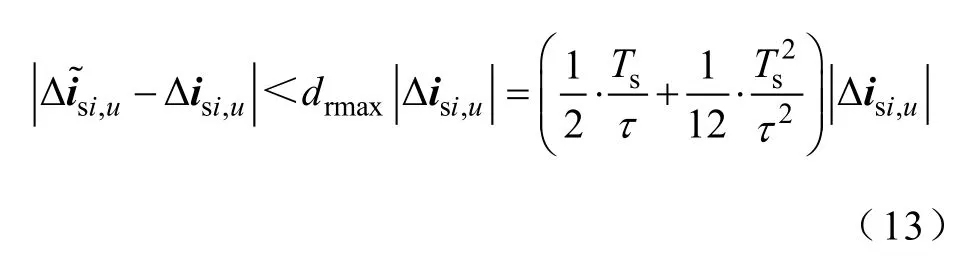
误差只与电气时间常数τ相关。针对不同的PMSM，Ts/τ值通常小于0.1，故可达到drmax＜5.1%，满足工程中偏差在10%以内的要求。相对误差的轮廓线如图3所示。

根据Ts的取值范围可以看出，图4中给出的转速范围较宽，具有一定的普适性。而实际预测中，对于额定转速10 000r/min以内的电机，截取至Ts的1次，该分量的预测误差已经非常小：对于两对极的电机，相对距离小于1%，四对极的将小于3%。

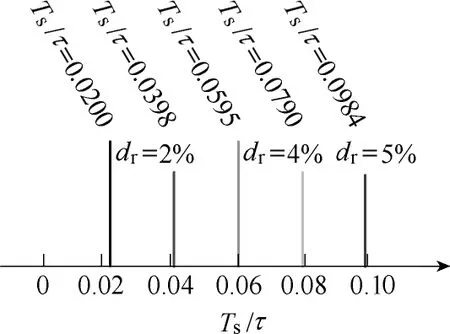
图3　Ts/τ 引起的预测误差轮廓曲线Fig.3 Error contour caused by Ts/τ

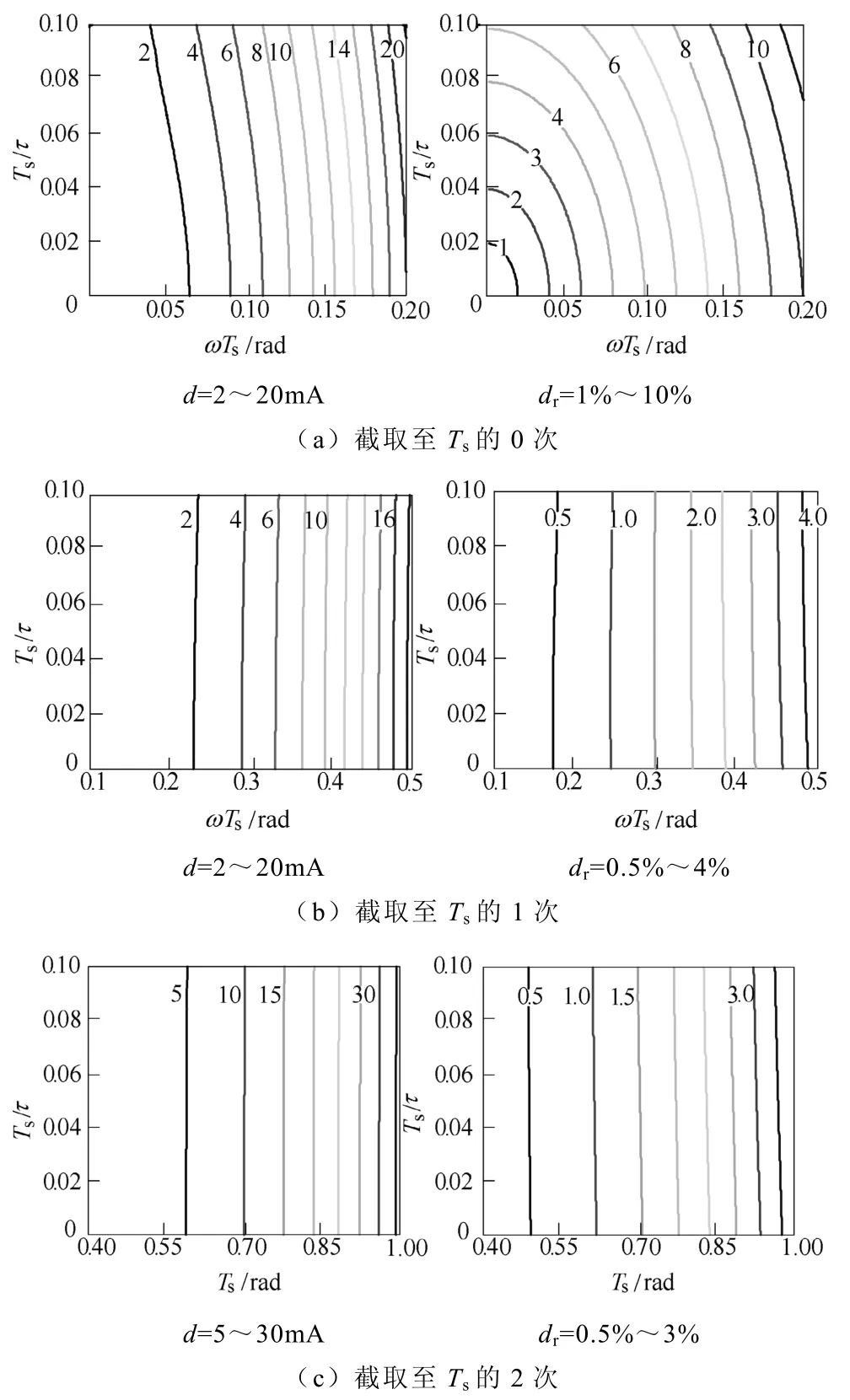
图4　矢量距离d和相对距离dr的轮廓曲线Fig.4 Profile curves of vector distance and relative distance

此外，因电机参数引起的误差，可利用在线辨识的方法进行参数修正。电机参数在线辨识的方法很多[12-14]，而电流预测的计算时间较短，在引入参数在线辨识时，不宜采用过于复杂的算法。文中可直接利用所提出的预测表达式，采用带遗忘因子的递推最小二乘法[15]辨识所需的Ls、Rs以及ψf等参数。

3 仿真及实验

3.1 预测算法误差的计算

以上从理论上分析了所提出的电流矢量预测方法的性能，以下针对某电机进行实验验证，实验电机选用KOLLMONGEN公司M205B型电机，该电机参数见表1。

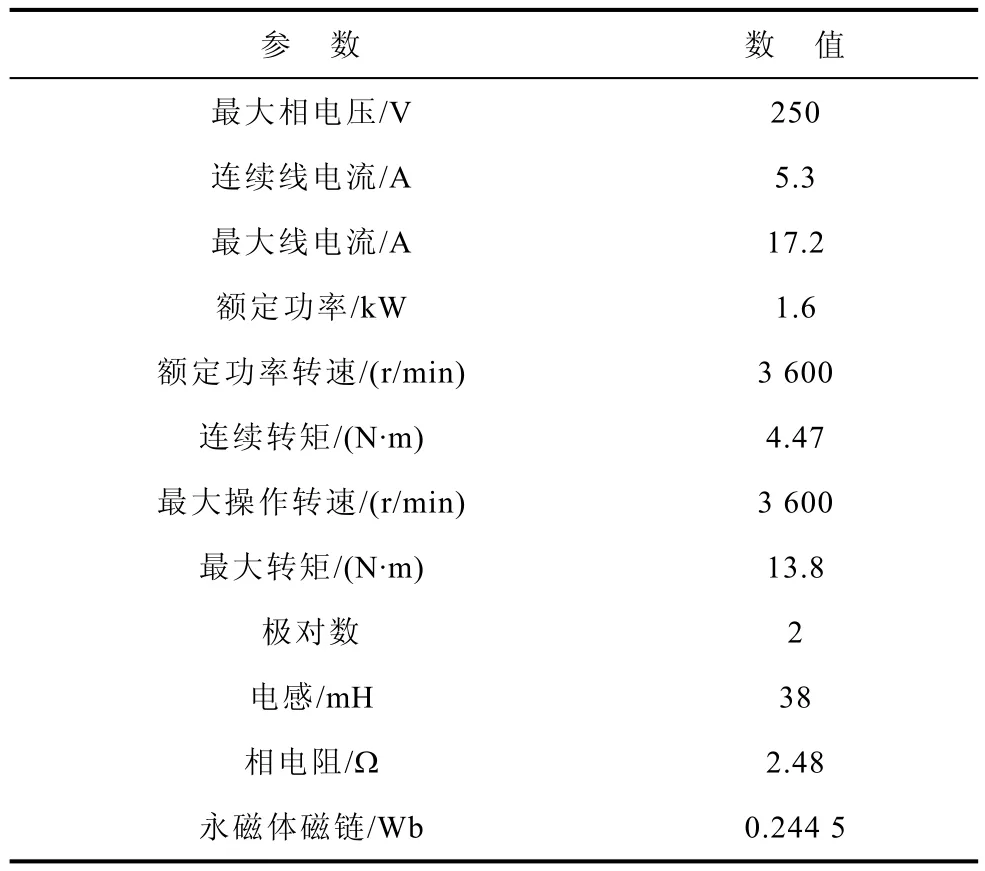
表1　电机参数Tab.1 Parameters of the PMSM

根据表1中参数可计算时间常数τ＝15.3ms。如果采样周期Ts＝0.1ms，Ts/τ＝0.006 53，利用式（11）计算预测电流，其分解矢量Δisi、Δisu近似计算相对距离均为0.33%。而对于Δisω项，通过计算得到近似阶次分别取0、1和2次时，不同转速下Δisω电流矢量的误差见表2（误差保留四位小数）。

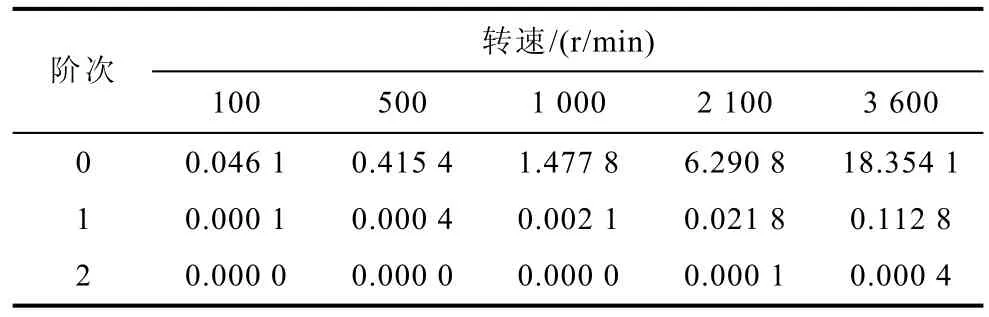
表2　电流矢量预测中Δisω项近似误差Tab.2 Error of Δisωin the current vector prediction　（单位：mA）

由表2可以看出，误差随转速的升高而增大，并且受近似程度的影响，阶次越高，偏差越接近0。对于该电机，表2中最大的偏差为18.354 1mA，相对距离3.7%，相对电机电流预测值是误差范围内可以忽略的，但考虑预测准确度，本文在后续的实验中，还将取到1阶的计算准确度。

3.2 PMSM电流矢量预测仿真实验

为检验本文预测算法的准确性，首先进行仿真实验。仿真电机模型参数同表1，在文献[16]离散电流控制方法的控制下，对电流矢量的动态变化进行预测。仿真条件为：直流母线电压200V，开关频率10kHz，同步采样周期100μs，给定电流矢量幅值恒为5A。以下对电流矢量阶跃变化以及连续运行情况进行仿真实验。

当给定电流矢量从电角度30°阶跃变化至60°，电流矢量的动态变化和预测结果如图5a所示；A相电流波形及其预测波形如图5b所示，图中由于两条曲线较为接近，故将预测电流波形向下平移1A的刻度以便于观测。

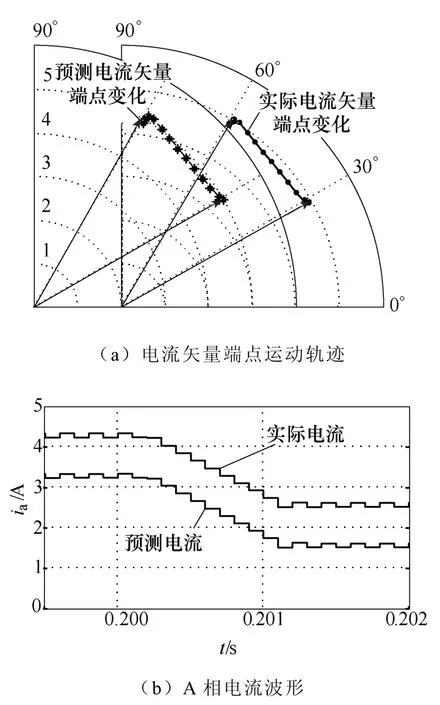
图5　电流矢量阶跃响应变化及预测结果Fig.5 Step response and predicting result of current vector

图5a中指向30°和60°的矢量表示阶跃变化前后的给定电流矢量，相应地，A相电流从4.33A变到2.5A。为清楚对比预测电流矢量端点轨迹及实际轨迹，将二者分别绘制在水平平移后的两个极坐标中，从图中可看出轨迹的一致性。图5b中电流波形是模拟采样过程经过0阶保持器所输出的电流波形，数值保持时间与采样周期相同。利用式（12）计算电流矢量的距离，如图6所示。从图6中可以看出，电流矢量不变时，距离值在4mA上下，阶跃变化处最大距离不超过11mA。

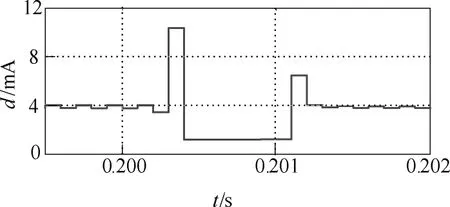
图6　预测与实际的电流矢量距离dFig.6 Distance d of the current vector

采用恒频控制方法控制电机连续运行，给定电流矢量按如图7所示的12个空间离散位置以逆时针顺序给定[17]。通过调节矢量的切换频率，即可控制电机按不同速度运行，其切换频率fconst与电机转速n的关系为n＝2.5fconst，电流基波频率fi＝fconst/12。

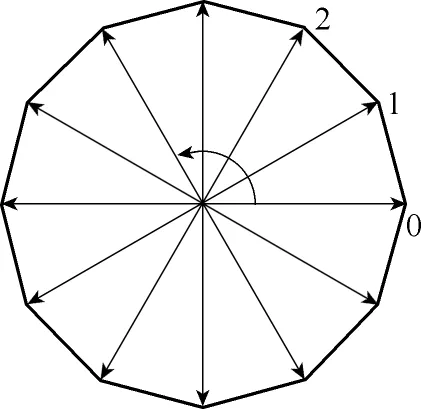
图7　给定离散电流矢量Fig.7 The given discrete current vectors

当给定fconst＝400Hz时，电流基波频率约为33.3Hz，电机恒定转速为1 000r/min，其实际电流矢量端点的空间轨迹以及预测矢量轨迹如图8a所示，A相电流波形如图8b所示，其中预测电流波形向下平移约2A。

从图8a中可看出预测的电流矢量端点轨迹与实际值基本一致，图8b电流波形也说明预测结果的准确性。计算其预测电流矢量与实际矢量的距离d，得到对应时间段的预测偏差曲线，如图9所示。距离d的数值大多小于11mA，电流矢量切换点处的距离最大不超过13mA，约为给定电流矢量幅值（5A）的0.26%，其预测偏差比较理想。

当给定fconst＝12Hz时，电流基波频率为1Hz，此时电机转速约30r/min。电流矢量端点的空间轨迹以及预测矢量轨迹如图10a所示，其A相电流波形对比如图10b所示，为清楚区分二者，将预测电流曲线向下平移2A。

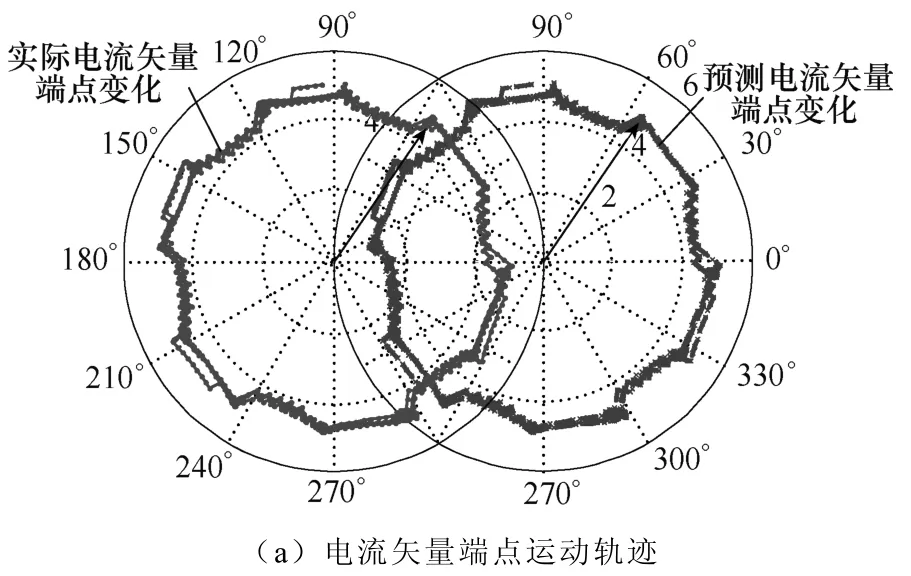
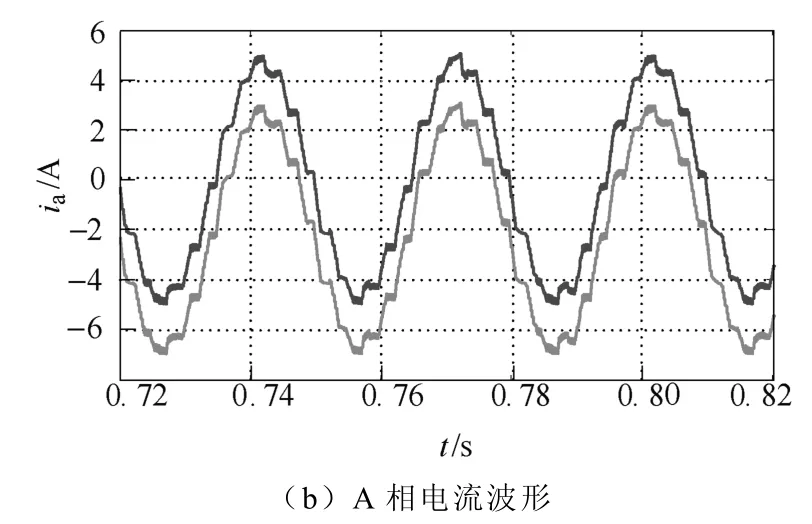
图8　1 000r/min速度下的电流矢量及预测结果Fig.8 Current vector and predicting results at speed of 1 000r/min

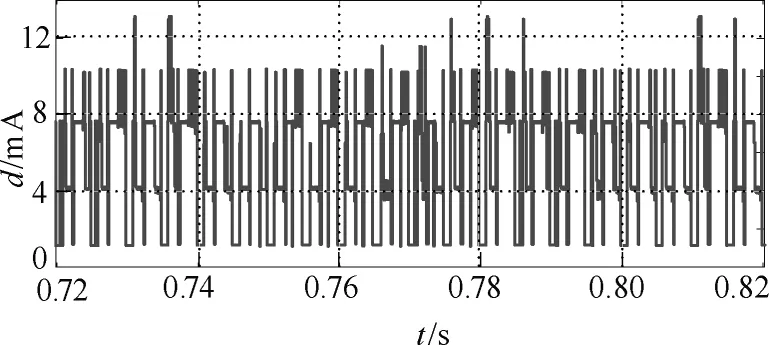
图9　预测与实际的电流矢量距离dFig.9 Distance d of the current vector

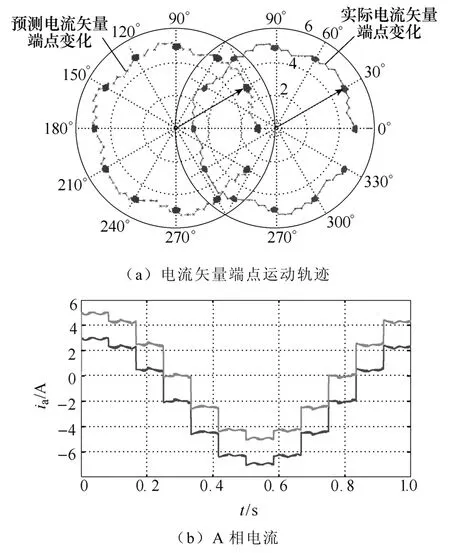
图10　1Hz电流基波频率下的电流矢量及预测结果Fig.10 Current vector and predicting result on frequency of 1Hz

图10a中可以看出，电流矢量轨迹基本一致，在较低的电流频率下，电流的动态预测效果仍然十分理想，从图10b中亦可看出A相电流波形的一致性。通过计算矢量距离偏差d，得到图11，其偏差最大值存在于电流矢量切换过程中，其值小于12mA，而在电流恒定的过程，预测矢量距离偏差在4mA上下浮动。

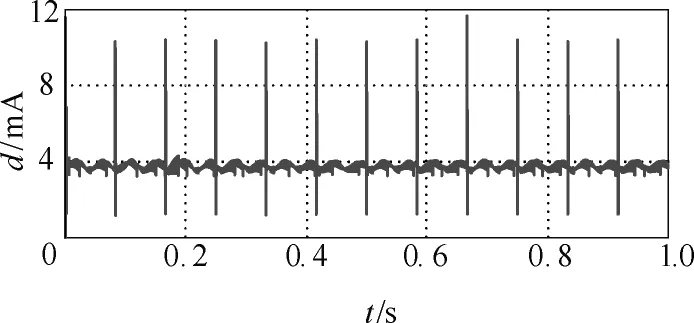
图11　预测与实际的电流矢量距离dFig.11 Distance d of the current vector

从仿真实验可以表明，本文所提出的电流预测方法有很好的效果，为电流预测控制提前计算控制量和减少控制延时提供了可靠的预测电流值。

3.3 PMSM电流矢量预测平台实验

实验所用的PMSM参数同表1，实验平台基于TMS320F2407为核心的DSP控制器，并包含AD转换和DA转换等电路，功率部分采用智能功率模块PM15RSH120对电机实施控制。预测计算在DSP中实现，经换算后由附带的DA转换模块输出预测结果和预测偏差至波形记录仪。给定电流矢量幅值为5A，直流母线电压200V，电机控制周期100μs，一个控制周期输出一次。电流波形均为A相电流。预测偏差以矢量距离d计算。

图12为电机以上述控制方法下的A相电流波形。由于预测电流与实测电流波形十分接近，为清楚对比，特别将预测电流向上平移三个小格。

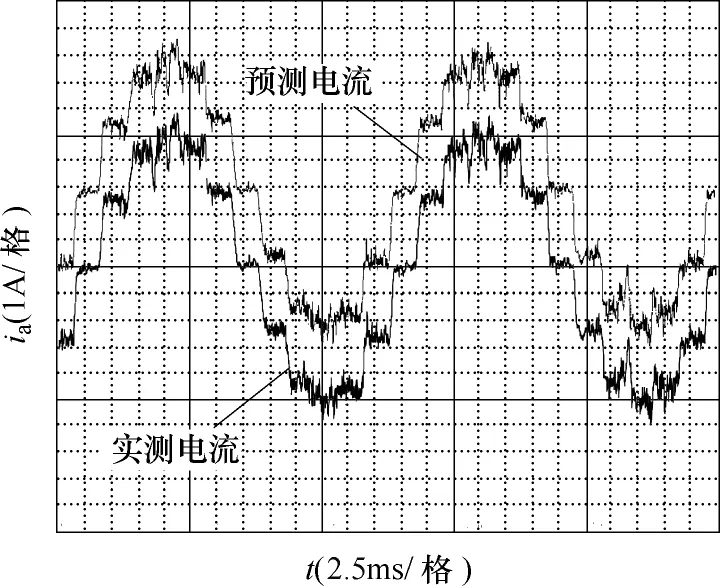
图12　1 000r/min时的A相实测电流和电流预测波形Fig.12 Actual and predicting A-phase current waveform at speed of 1 000r/min

通过计算得到的输出电流矢量距离d如图13所示。通过数据计算的距离均值为120mA，为给定电流矢量幅值（5A）的2.4%。

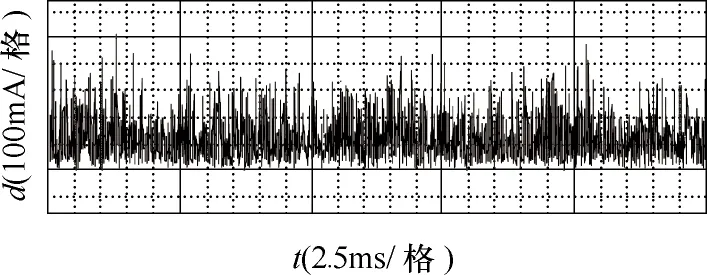
图13　预测与实际的电流矢量距离dFig.13 Distance d of the current vectors

当电机按照电流基波频率1Hz运行时，其A相电流波形如图14所示，电机转速30r/min，同样将预测电流波形向上平移三个小格。

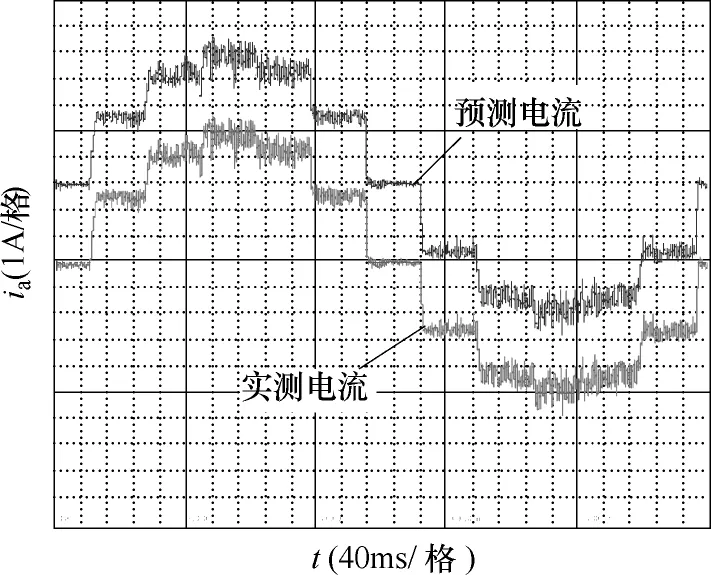
图14　30r/min时的A相实测电流和电流预测波形Fig.14 Actual and predicting A-phase current waveform at speed of 30r/min

计算并用DA输出电流矢量距离d如图15所示，其距离均值为82.6mA，约为给定电流矢量幅值（5A）的1.65%。

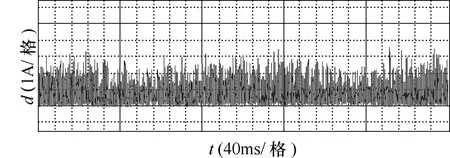
图15　预测与实际的电流矢量距离dFig.15 Distance d of the current vectors

以上实验可以说明本文所提出的算法在实际电机控制应用中同样具有良好的效果。

4 结论

高性能的PMSM电机控制系统对电流环要求较高，本文提出的以电流矢量为目标的电流预测方法可以准确地预测电流矢量的变化趋势。通过分析PMSM电流的动态响应，将电流矢量在离散周期上的变化量分解为三个独立的分量，并利用泰勒级数得到易于实现的近似表达式，从而实现了电流矢量的动态预测。同时，误差分析给出了算法的准确性，尤其是对反电动势引起的电流矢量变化，给出了不同速度下不同阶次的通用表达式，并得出误差的轮廓线图，为匹配相应转速下预测计算的参数选择提供了理论依据，并由仿真进行了验证。最后通过实验得出不同转速下的预测偏差，实验结果证明了本文提出的电流矢量预测算法具有良好的性能，对提高电流控制的准确度和跟随速度有十分重要的意义。

参考文献

[1]Moon H T,Youn M J.Predictive current control for PMSM with consideration of calculation delay[J].Electronics Letters,2001,37（24）:1488-1489.

[2]Abu-Rub H,Guzinski J,Krzeminski Z,et al.Predictive current control of voltage source inverters[J].IEEE Transactions on Industrial Electronics Society,2004,51（3）:585-593.

[3]陈书锦,李华德,李擎,等.永磁同步电动机起动过程控制[J].电工技术学报,2008,23（7）:39-44.Chen Shujin,Li Huade,Li Qing,et al.Start process control of permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2008,23（7）:39-44.

[4]Weigold J,Braun M.Predictive current control using identification of current ripple[J].IEEE Transactions on Industrial Electronics,2008,55（12）:4346-4353.

[5]Sakata K,Fujimoto H,Peretti L,et al.Enhanced speed and current control of PMSM drives by perfect tracking algorithms[C]//The International Power Electronics Conference,2010:587-592.

[6]牛里,杨明,刘可述,等.永磁同步电机电流预测控制算法[J].中国电机工程学报,2012,32（6）:131-137.Niu Li,Yang Ming,Liu Keshu,et al.A predictive current control scheme for permanent magnet synchronous motors[J].Proceedings of the CSEE,2012,32（6）:131-137.

[7]牛里,杨明,王庚,等.基于无差拍控制的永磁同步电机鲁棒电流控制算法研究[J].中国电机工程学报,2013,33（15）:78-85.Niu Li,Yang Ming,Wang Geng,et al.Research on the robust current control algorithm of permanent magnet synchronous motor based on deadbeat control principle [J].Proceedings of the CSEE,2013,33（15）:78-85.

[8]杨南方,骆光照,刘卫国.误差补偿的永磁同步电机电流环解耦控制[J].电机与控制学报,2011,15（10）:50-54,62.Yang Nafang,Luo Guangzhao,Liu Weiguo.Decoupling control of current loop for permanent magnet synchronous motor drives using error compensation[J].Electric Machines and Control,2011,15（10）:50-54,62.

[9]万山明,吴芳,黄声华.永磁同步电机的数字化电流控制环分析[J].华中科技大学学报:自然科学版,2007,35（5）:48-51.Wan Shanming,Wu Fang,Huang Shenghua.Analysis of digital current control loop for a PMSM[J].Journal of Huazhong University of Science and Technology（Nature Science Edition）,2007,35（5）:48-51.

[10]Ambrozic V,Fiser R,Nedeljkovic D.Direct current control-a new current regulation principle,IEEE Transactions on Power Electronics,2003,18（1）:495-503.

[11]王伟华,肖曦,丁有爽.永磁同步电机改进电流预测控制[J].电工技术学报,2013,28（3）:50-55.Wang Weihua,Xiao Xi,Ding Youshuang.An improved predictive current control method for permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2013,28（3）:50-55.

[12]徐东,王田苗,刘敬猛,等.基于参数辨识的永磁同步电机电流精确控制方法[J].电力自动化设备,2008,28（11）:30-35.Xu Dong,Wang Tianmiao,Liu Jingmeng,et al.Precise current control of PMSM based on parameter identification[J].Electric Power Automation Equipment,2008,28（11）:30-35.

[13]王松,刘明光,石双双,等.基于卡尔曼滤波和神经网络的PMSM参数辨识[J].北京交通大学学报,2010,34（2）:124-127,136.Wang Song,Liu Mingguang,Shi Shuangshuang,et al.Identification of PMSM based on EKF and Kalman neural network[J].Journal of Beijing Jiaotong University,2010,34（2）:124-127,136.

[14]刘朝华,李小花,周少武,等.面向永磁同步电机参数辨识的免疫完全学习型粒子群算法[J].电工技术学报,2014,29（5）:118-126.Liu Zhaohua,Li Xiaohua,Zhou Shaowu,et al.Comprehensive learning particle swarm optimization algorithm based on immune mechanism for permanent magnet synchronous motor parameter identification[J].Transactions of China Electrotechnical Society,2014,29（5）:118-126.

[15]杨立永,张云龙,陈智刚,等.基于参数辨识的PMSM电流环在线自适应控制方法[J].电工技术学报,2012,27（3）:86-91.Yang Liyong,Zhang Yunlong,Chen Zhigang,et al.On-line adaptive control of PMSM current-loop based on parameter identification[J].Transactions of China Electrotechnical Society,2012,27（3）:86-91.

[16]Dong Yan,Jing Kai,Sun Hexu,et al.Discrete current control strategy of permanent magnet synchronous motors[J].Journal of Applied Mathematics,2013（22）:1-9.

[17]董砚,孙鹤旭,包致远,等.基于矩角控制的永磁同步电动机位置控制系统[J].电工技术学报,2006,21（1）:86-91.Dong Yan,Sun Hexu,Bao Zhiyuan,et al.Permanent magnet synchronous motor position control system based on torque-angle control[J].Transactions of China Electrotechnical Society,2006,21（1）:86-91.

荆 锴 男，1987年生，博士研究生，研究方向为电机系统及其控制。

E-mail:jingkai_1082@126.com

孙鹤旭 男，1956年生，教授，博士生导师，研究方向为工程系统与控制。

E-mail:hxsun@hebut.edu.cn（通信作者）

Stator Current Dynamic Prediction of Permanent Magnet Synchronous Motor Targeting the Current Vector

Jing Kai1Sun Hexu1,2Dong Yan1Zheng Yi1
（1.School of Control Science and Engineering Hebei University of Technology Tianjin 300130 China 2.Hebei University of Science and Technology Shijiazhuang 050018 China）

AbstractThis paper proposed a dynamic prediction method for stator current of permanent magnet synchronous motor（PMSM）,targeting the current vector.The dynamic response of the current vector has been studied on the αβ stationary frame,and the vector is decomposed into three components caused by different actions.Each component is truncated and approximated by Taylor series,and the proposed method is thereafter obtained.In addition,through the error analysis of each component,a basis of parameter selection and application is provided.Experiments verify the accuracy of the prediction method.

Keywords：Permanent magnet synchronous motor,current vector,current prediction,error analysis

作者简介

收稿日期2014-03-21 改稿日期 2014-06-24

中图分类号：TM341