不同绕组型式双移30°六相永磁同步电机建模与谐波电流优化控制

郭新华 陈 银 尚荣艳 边元均 郭保甲

（华侨大学信息科学与工程学院 厦门 361021）



郭新华 陈 银 尚荣艳 边元均 郭保甲

（华侨大学信息科学与工程学院 厦门 361021）

摘要基于空间矢量解耦方法，建立绕组正弦和非正弦分布的双移30°六相永磁同步电机旋转坐标系下数学模型；为了减小谐波子空间电流，研究了谐波电流闭环控制和谐波电压开环控制两种控制方法，得出两种控制方式下相电流FFT分析结果。仿真和实验结果表明：谐波电流闭环控制方式对绕组正弦和非正弦两种电机具有更好的电流谐波控制效果，可以减小系统损耗，该方法更适合于双移30°六相永磁同步电机的控制。

关键词：六相电机 数学模型 解耦 谐波电流 闭环控制

国家自然科学基金面上项目（51477058），福建省自然科学基金面上项目（2013J01198）和华侨大学中青年教师科研提升资助计划（ZQN-YX304）资助。

0 引言

与传统的三相电机相比，多相电机具有转矩密度高、效率高、转矩脉动小和容错能力强等突出优点，多相电机在舰船推进和电力机车等中低压大功率、高性能和高可靠性等场合应用广泛[1-4]。随着电力电子技术、数字控制技术以及控制理论的发展，在开关器件开关频率受限的中压大功率传动系统的控制策略、多相电机容错控制技术以及抑制多相电机谐波电流控制方法等方面都有广泛的研究[5-9]。

文献[10]提出基波矢量控制，该控制方式有谐波电流不可控的问题；文献[1,11]对空间矢量解耦控制方法进行研究，但是提出的调制算法使有的开关器件在一个PWM周期内开关次数不止一次，且当电机相数增加时，PWM算法难度大幅增加，因此在系统实际应用中受到限制。

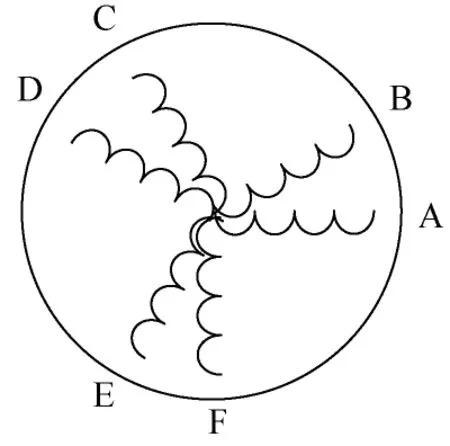
图1　双移30°永磁同步电机结构示意图Fig.1 Structure diagram for six-phase permanent magnet synchronous motor with two-connected windings displaced by 30°

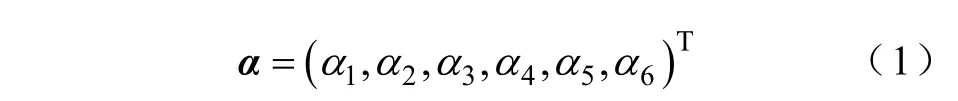
绕组正弦分布电机绕组函数及永磁磁链方程分别为

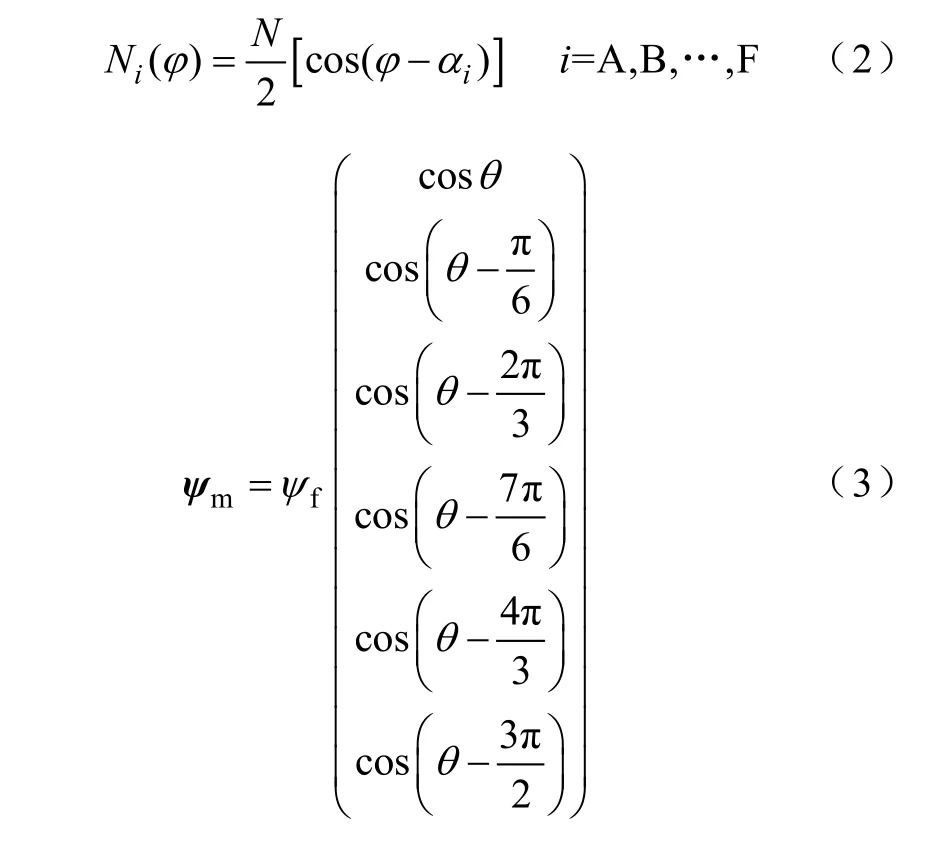
式中，ϕ 为空间角度；θ 为转子位置角度；N为每相绕组匝数；ψm为永磁磁链；ψf为永磁基波磁链幅值。

绕组非正弦分布电机，考虑5次谐波的影响，绕组函数及永磁磁链方程分别为

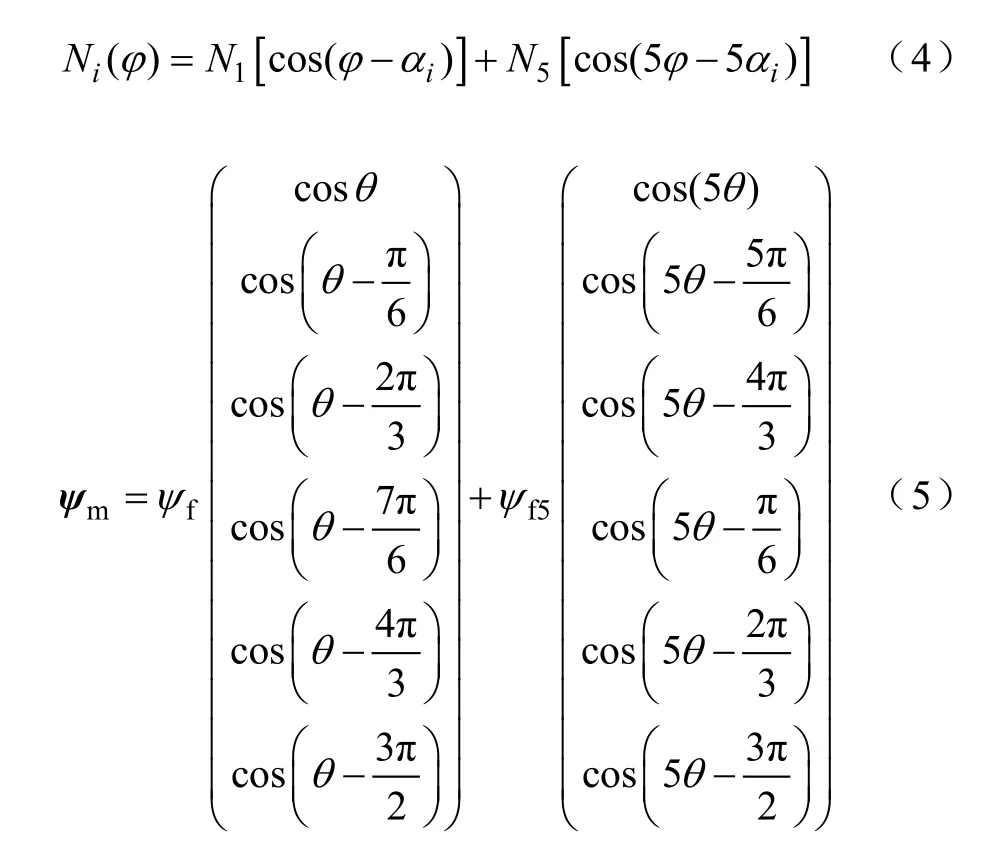
式中，N1为绕组基波幅值；N5绕组5次谐波幅值；ψf5为永磁5次谐波磁链幅值。

绕组正弦和非正弦分布电机解耦变换矩阵分别如式（6）和式（7）所示，解耦变换后，双移30°永磁同步电机六维变量被分别投影到相互垂直的三个两两互相垂直的子平面上[1]，由自然坐标系下的电机模型变换到旋转坐标系，新坐标系由α-β子空间、z1-z2广义零序子空间和o1-o2零序子空间组成。电机中的k＝12m±1（m＝1,3,5,··）次谐波被完全投影到α-β平面，该平面的变量与机电能量转换有关，由于最低次谐波为11次，忽略高次谐波，可认为该平面只有基波分量；6m±1（m＝1,3,5,··）次谐波投影在z1-z2平面；6m±3（m＝1,3,5,··）次谐波投影在o1-o2平面，双移30°永磁同步电机两套联结的三相绕组，中性点间不连接，定子电流中不包含3次谐波在内的零序分量。

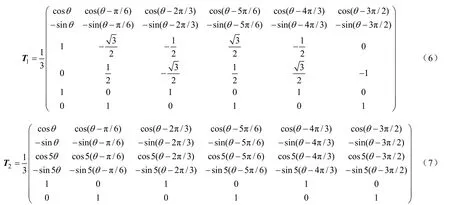
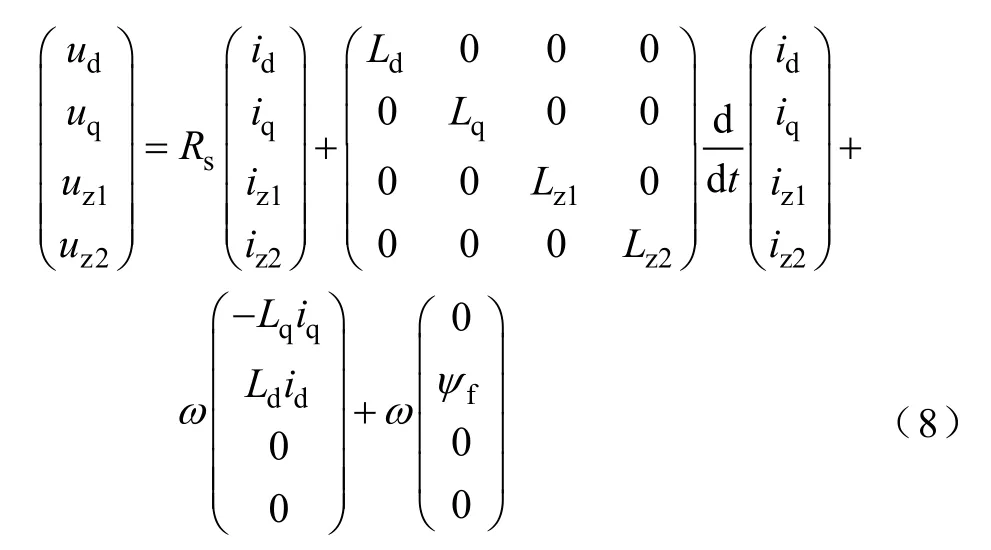
电磁转矩方程为

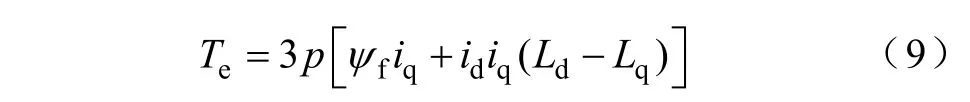
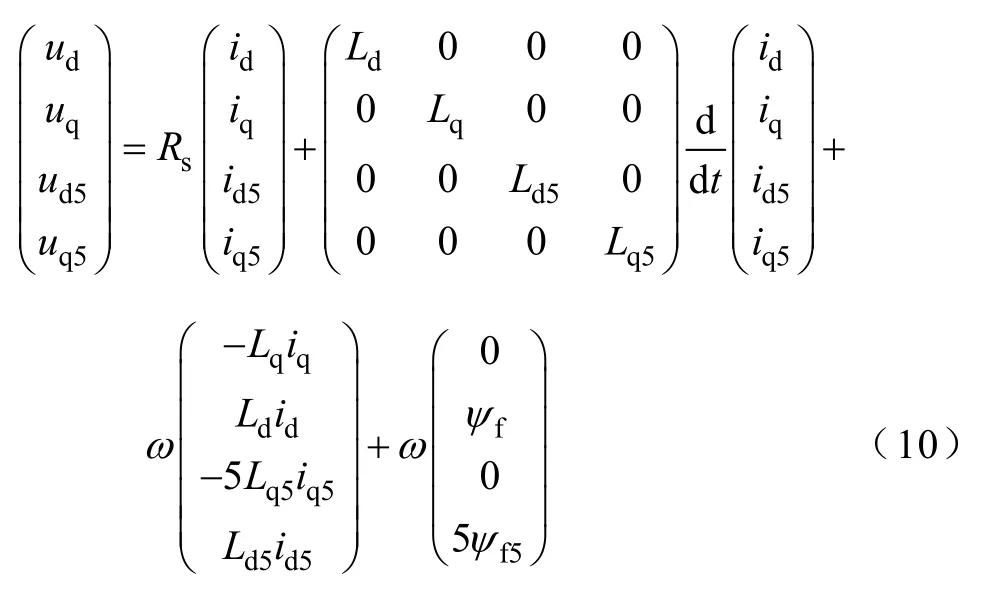
电磁转矩方程为

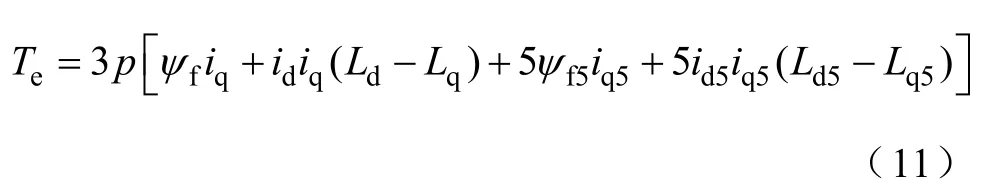
式中，ud、uq，id、iq和Ld、Lq分别为基波平面dq轴上电压、电流和电感；uz1、uz2，iz1、iz2和Lz1、Lz2分别为绕组正弦分布电机谐波平面上电压、电流和漏电感；ud5、uq5，id5、iq5和Ld5、Lq5分别为绕组非正弦电机5次谐波平面d、q轴上的电压、电流和电感；Rs、ω、Te和p分别为电机的定子电阻、电角速度、电磁转矩和极对数。通过解耦变换后，电机数学模型更加简单，基波与谐波之间实现解耦，对电机的分析与控制得到简化。

2 基于载波的PWM控制系统

基于载波的PWM控制是根据载波周期内的伏秒平衡原理发展起来的，该算法只有加和乘两种运算，适用于任意多相的变频调速系统，且逆变器开关器件在一个周期内只开关一次，可以缩短微处理器的运算时间[12,13]。

逆变器每相PWM开关信号在一个周期Ts内有效的电压输出时间为Teff，可以称之为“有效作用时间”，只有在Teff内才有逆变器到负载的有功流动。设六相载波PWM一个周期内各相输出的参考电压分别为Uas、Ubs、Ucs、Uds、Ues和Ufs，关断时间分别为Tas、Tbs、Tcs、Tds、Tes和Tfs，如图2a所示。载波PWM周期内输出的平均电压应该等于参考电压，则关断时间与参考电压的关系式为

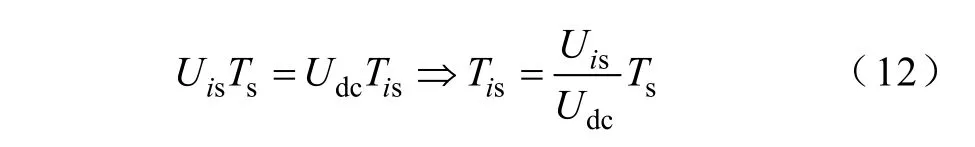
式中，Udc为逆变器直流母线电压；i＝a,b,c,d,e,f。

因为参考电压有正、负，所以Tas、Tbs、Tcs、Tds、Tes和Tfs也有可能是负值，称之为“虚拟时间”。在Tas、Tbs、Tcs、Tds、Tes和Tfs中求出最大值记为Tmax，最小值记为Tmin，则Teff表达式为

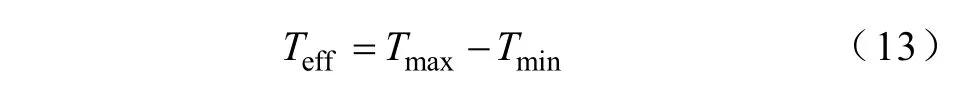
决定Teff大小的是伏秒平衡原理，由于Teff位置是任意的，所以引入一个变量Toffset来描述Teff的不同位置，Toffset的表达式为

为保证每相PWM实际触发时刻在0～Ts之间，需加约束条件

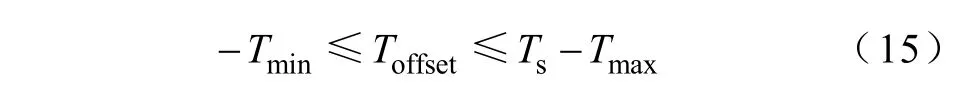
载波PWM在一个周期内对称，则每相开通关断时间即可求出，开通和关断时间分别设为Ti_on，Ti_off（i＝a,b,··,f），数值表达式为

图2为六相载波PWM的产生过程。

对绕组正弦分布电机，α-β平面与电机的机电能量转换有关，z1-z2平面电压方程中只含有漏感和定子电阻分量，阻抗小，因此应该控制电压尽可能小，抑制谐波电流，减小电机损耗；对绕组非正弦分布电机，z1-z2平面与电机的机电能量转换有关，理论上，可以利用谐波同步转矩，但是谐波同步转矩的利用条件比较苛刻[14]，应抑制谐波电流。文献[15]也主要对抑制绕组非正弦分布九相感应电机谐波电流的方法进行分析。经过以上分析，对绕组正弦和非正弦分布的电机可使用谐波平面谐波电流闭环控制和谐波电压开环控制，以减小谐波电流分量，控制框图如图3和图4所示。

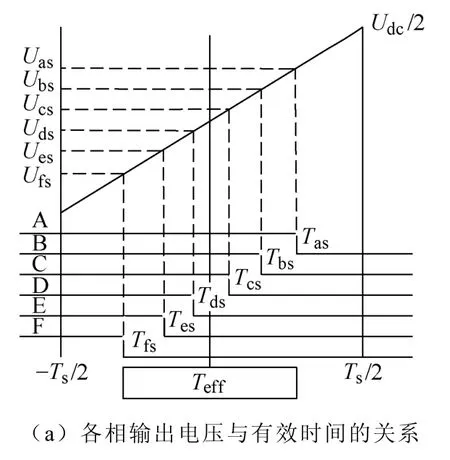
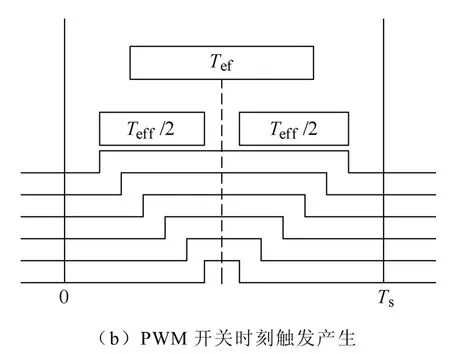
图2　六相载波示意图Fig.2 Schematic diagram of six-phase carrier

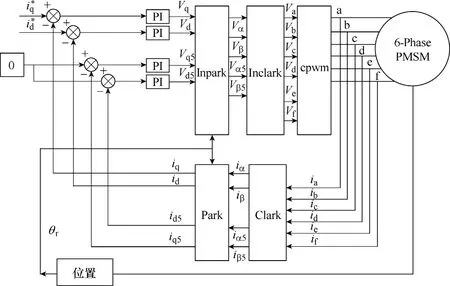
图3　谐波电流闭环控制框图Fig.3 Closed-loop harmonic current control diagram

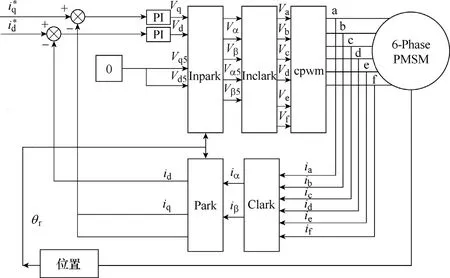
图4　谐波电压开环控制框图Fig.4 Open-loop harmonic voltage control diagram

3 仿真与实验

3.1 仿真与结果分析

本文基于Matlab/Simulink仿真平台建立了绕组正弦和非正弦分布双移30°六相永磁同步电机在谐波电压开环及谐波电流闭环控制方式下仿真模型。绕组正弦分布电机仿真参数：Rs＝0.05Ω，Ld＝0.9mH，Lq＝2.1mH，Lz1＝0.345mH，Lz2＝0.345mH，ψf＝0.05Wb，p＝4。

绕组非正弦分布电机仿真参数：Rs＝0.05Ω，Ld＝0.9mH，Lq＝2.1mH，Ld5＝0.345mH，Lq5＝0.405mH，ψf＝0.05Wb，ψf5＝-0.003 5Wb，p＝4。

绕组正弦和非正弦分布电机在谐波电压开环控制及谐波电流闭环控制方式下仿真。仿真系统在直流母线电压为300V，转速为600r/min，负载转矩为37N·m的情况下，相电流波形及FFT分析分别如图5～图8所示，不同绕组型式电机在两种控制方式下仿真相电流的THD值和低次谐波含量见表1和表2。

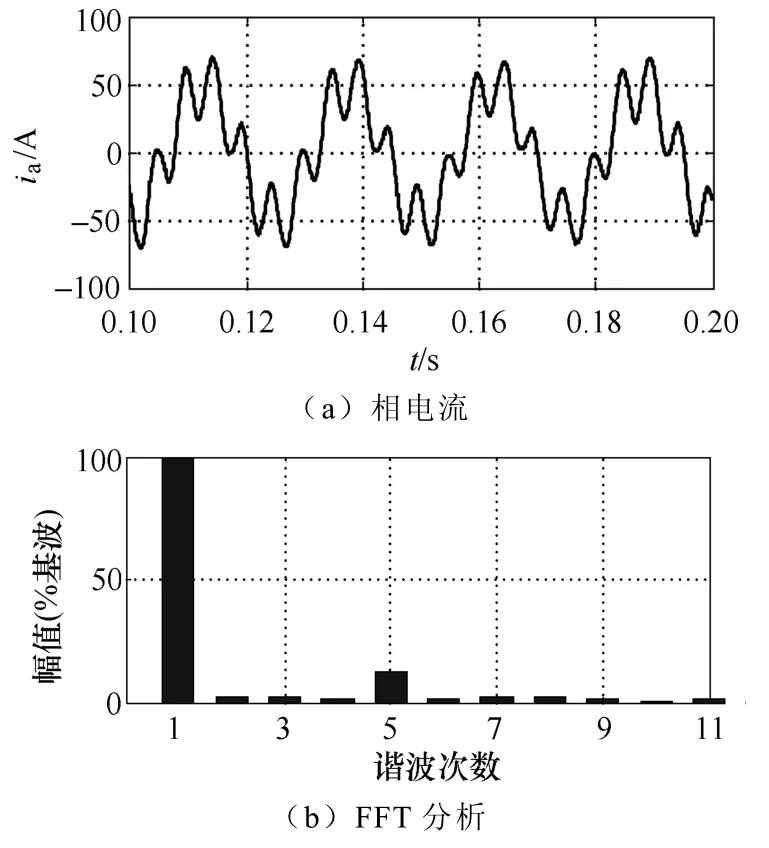
图5　谐波电压开环控制方式下绕组正弦电机相电流仿真波形及FFT分析Fig.5 Phase current waveforms and FFT analysis results for sinusoidal winding motor with harmonic voltage open-loop control mode

由仿真实验可以看出，绕组正弦分布电机谐波电压开环控制相电流THD为39.71%，谐波电流闭环控制下相电流THD为1.73%，且5次和7次谐波得到很好的控制。同样对绕组非正弦分布电机谐波电流闭环控制也有相同的效果。

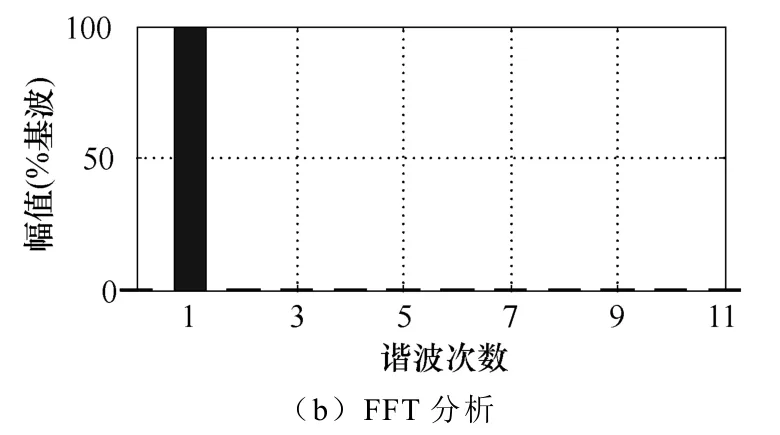
图6　谐波电流闭环控制方式下绕组正弦电机相电流仿真波形及FFT分析Fig.6 Phase current waveforms and FFT analysis results for sinusoidal winding motor with harmonic current close-loop control mode

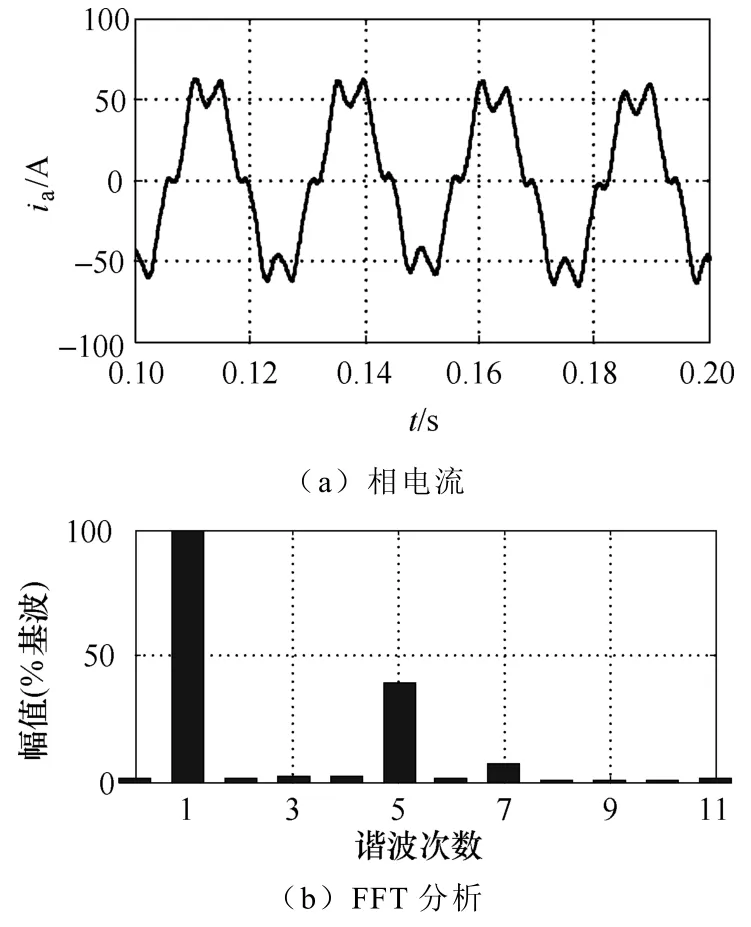
图7　谐波电压开环控制方式下绕组非正弦电机相电流仿真波形及FFT分析Fig.7 Phase current simulation and FFT analysis results for non-sinusoidal winding motor with harmonic voltage open-loop control mode

3.2 实验与结果分析

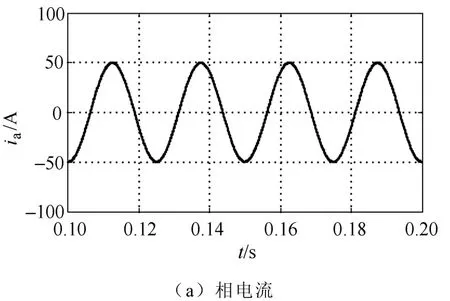
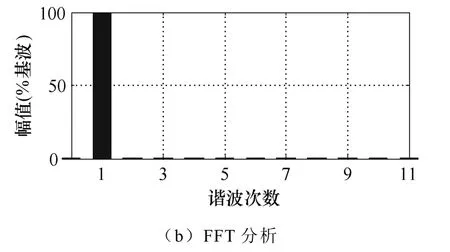
图8　谐波电流闭环控制方式下绕组非正弦电机相电流仿真波形及FFT分析Fig.8 Phase current simulation and FFT analysis results for non-sinusoidal winding motor with harmonic current close-loop control mode

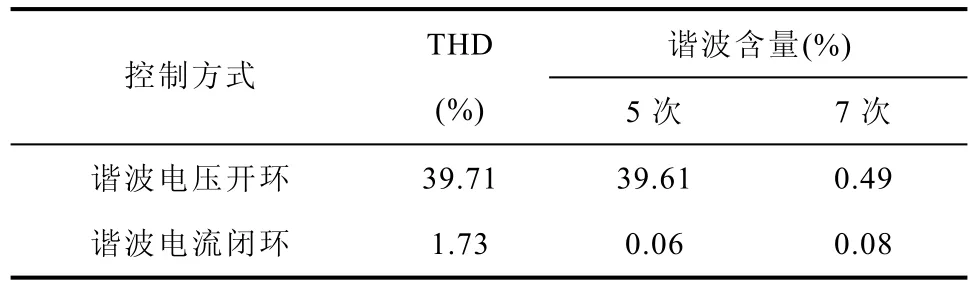
表1　绕组正弦电机仿真相电流谐波含量（仿真结果）Tab.1 Harmonic current content of sinusoidal winding motor phase current（simulation results）

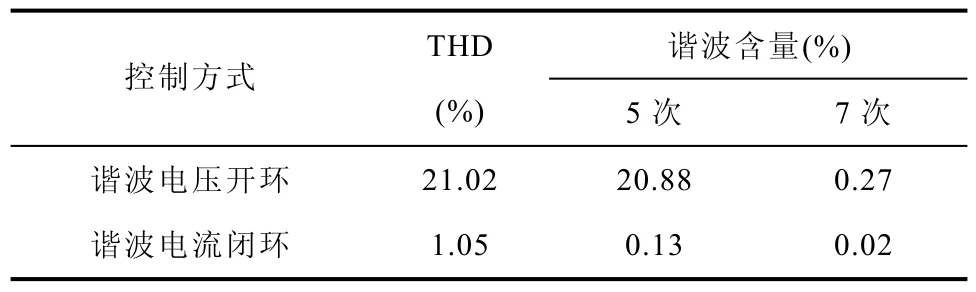
表2　绕组非正弦电机仿真相电流谐波含量（仿真结果）Tab.2 Harmonic current content of non-sinusoidal winding motor phase current（simulation results）

图9　谐波电压开环控制方式下相电流实验波形及FFT分析Fig.9 Motor phase currents experimental waveform and FFT analysis result of harmonic voltage open-loop control mode

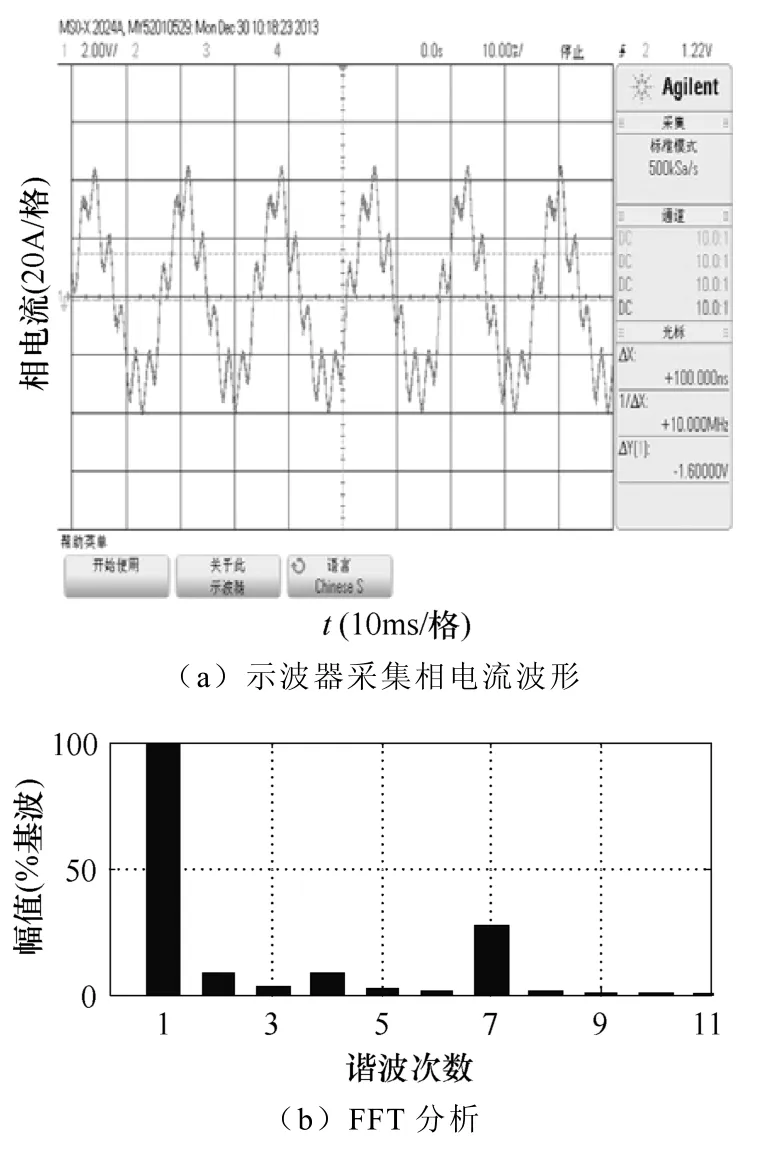
图10　谐波电流闭环制方式下相电流实验波形及FFT分析Fig.10 Motor phase currents experimental waveform and FFT analysis result of harmonic current closed-loop control mode

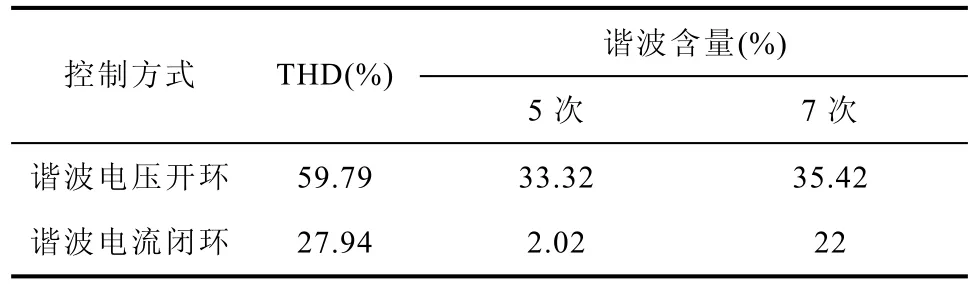
表3　相电流谐波含量数据表Tab.3 Data table for harmonic content of phase currents

在以上实验控制系统中，电机采用集中绕组，为绕组非正弦分布电机，并且控制系统忽略除5次谐波以外的高次谐波以及基波与谐波之间的耦合，所以从实验数据表3和仿真数据表2可知在谐波电压开环和谐波电流闭环两种控制方式下实验测得相电流THD值和5次、7次谐波含量都相对仿真实验的数值偏大，同时从实验数据表3看出谐波电流闭环控制相对于谐波电压开环控制时相电流THD值从59.79%减小到27.94%，5次谐波含量从33.32%减小到2.02%，7次谐波含量从35.42%减小到22%，可见谐波电流闭环控制优化了谐波电流，提高了控制系统性能。

4 结论

附 录

附图1　双移30°六相永磁同步电机及控制器App.Fig.1 Six-phase permanent magnet synchronous motor with two-connected windings displaced by 30° and its controller

附图2　测试台架App.Fig.2 Test bench

参考文献

[1]Zhao Yifan,Thomas A L.Space vector PWM control of dual three-phase induction machine using vector space decomposition[J].IEEE Transactions on Industry Applications,1995,31（5）:1100-1109.

[2]Emil Levi.Multiphase electric machines for variablespeed applications[J].IEEE Transactions on Industrial Electronics,2008,55（5）:1893-1909.

[3]薛山.多相永磁同步电机驱动技术研究[D].北京:中国科学院电工研究所,2005.

[4]薛山,温旭辉,王又珑.多相永磁同步电机多维控制技术[J].电工技术学报,2008,23（9）:65-69.Xue Shan,Wen Xuhui,Wang Youlong.Multidimensional control in multiphase permanent motor drives[J].Transactions of China Electrotechnical Society,2008,23（9）:65-69.

[5]程启明,程尹曼,王映斐,等.交流电机控制策略的发展综述[J].电力系统保护与控制,2011,39（9）:145-154.Cheng Qiming,Cheng Yiman,Wang Yingfei,et al.Overview of control strategies for AC motor[J].Power System Protection and Control,2011,39（9）:145-154.

[6]郭新华,王永兴,赵峰,等.基于SHEPWM的中压大功率牵引永磁同步电机两电平控制[J].电工技术学报,2012,27（11）:76-82.Guo Xinhua,Wang Yongxing,Zhao Feng,et al.Two level control technology of PMSM used in medium voltage high power traction system based on SHEPWM[J].Transactions of China Electrotechnical Society,2012,27（11）:76-82.

[7]袁飞雄,黄声华,龙文枫.六相永磁同步电机谐波电流抑制技术[J].电工技术学报,2011,26（9）:31-36.Yuan Feixiong,Huang Shenghua,Long Wenfeng.Techniques to restrain harmonics of six-phase permanent magnet synchronous motors[J].Transactions of China Electrotechnical Society,2011,26（9）:31-36.

[8]杨金波,李铁才,杨贵杰.一相开路双三相永磁同步电机建模与控制[J].电工技术学报,2011,26（10）:167-173.Yang Jinbo,Li Tiecai,Yang Guijie.Modeling and control of dual three-phase PMSM with one open phase[J].Transactions of China Electrotechnical Society,2011,26（10）:167-173.

[9]刘自程,郑泽东,彭凌,等.船舶电力推进中十五感应电机同轴运行及容错控制策略[J].电工技术学报,2014,29（3）:65-74.Liu Zicheng,Zheng Zedong,Peng Ling,et al.Fixed joint double fifteen-phase induction motor control and fault-tolerant control in ship propulsion system[J].Transactions of China Electrotechnical Society,2014,29（3）:65-74.

[10]Kianinezhad R,Nahid B,Betin F,et al.A new field orientation control of dual three phase induction machines[C].Proceedings of International Conference on Industrial Technology,2004:187-192.

[11]孟超,欧阳红林,刘伟侯,等.双移30°永磁同步电机的空间矢量调制[J].中国电机工程学报,2010,30（3）:90-98.Meng Chao,Ouyang Honglin,Liu Weihou,et al.Space-vector PWM techniques for dual Y shift 30 degree permanent-magnet synchronous motor[J].Proceedings of the CSEE,2010,30（3）:90-98.

[12]Li E Levi,Dujic D,Jones M,et al.Analytical determination of DC-bus utilization limits in multiphase VSI supplied AC drives[J].IEEE Transactions on Energy Conversion,2008,23（2）:433-443.

[13]Yuan M Hava,Kerkman R J,Lipo T A.Simple analytical and graphical tools for carrier based PWM methods[C].Proceedings of IEEE Power Electronics Specialists Conference,1997,2:1462-1471.

[14]王又珑.十五相感应电机磁场分析及驱动技术研究[D].北京:中国科学院电工研究所,2009.

[15]梅柏杉,冯江波,吴迪.基于谐波电流闭环控制的九相感应电机矢量控制系统[J].电机与控制应用,2014,41（10）:15-19.Mei Boshan,Feng Jiangbo,Wu Di.Nine-phase induction motor vector control system based on the harmonic current closed-loop control strategy[J].Electric Machines ＆ Control Application,2014,41（10）:15-19.

郭新华 男，1977年生，博士，副教授，研究方向为电动汽车用永磁型双机械端口电机驱动控制、永磁同步电机驱动控制、异步电机驱动控制、中压大功率牵引永磁（异步）电机控制和六相永磁同步电机控制。

E-mail:guoxinhua@hqu.edu.cn（通信作者）

陈 银 男，1989年生，硕士研究生，研究方向为电机系统及其控制。

E-mail:550603197@qq.com

Modeling and Optimized Harmonic Current Control for Six-Phase Permanent Magnet Synchronous Motor with Two-Connected Windings Displaced by 30° in Different Winding Types

Guo Xinhua Chen Yin Shang Rongyan Bian Yuanjun Guo Baojia
（Huaqiao University Xiamen 361021 China）

AbstractBased on the method of space vector decoupling,mathematical models are established in rotating coordinate system separately for six-phase permanent magnet synchronous motors,which are manufactured with two sinusoidal or non-sinusoidal-connected windings displaced by 30°.In order to reduce the currents in harmonic subspace,methods of harmonic current closed-loop control and harmonic voltage open-loop control are studied respectively,and FFT analyzed results of phase currents are obtained.Simulation and experimental results imply that harmonic current closed-loop control mode has a better performance in limiting harmonic currents of both sinusoidal and non-sinusoidal winding motors,and the system losses can also be reduced.This control method is more suitable for control of six-phase permanent magnet synchronous motor with two-connected windings displaced by 30°.

Keywords：Six-phase motor,mathematical model,decoupling,harmonic currents,closed loop control

作者简介

收稿日期2014-10-29 改稿日期 2015-07-31

中图分类号：TM351