基于类刚度系数的离心力矩返回机构周期计算

张跃丽，王发林

(西安机电信息技术研究所，西安　710065)



基于类刚度系数的离心力矩返回机构周期计算

张跃丽，王发林

(西安机电信息技术研究所，西安710065)

摘要：针对微尺度条件下利用离心力矩返回的非自由式擒纵装置缺乏理论计算依据，提出了“类刚度系数”的概念，并据此使用传统非自由式擒纵装置周期公式计算了该机构的平衡摆振动周期，该机构的平衡摆振动周期随驱动力变化，可实现解除保险距离恒定。通过仿真计算得到的振动周期数据与试验数据基本一致，证明提出“类刚度系数”的概念是合理的，同时经过仿真计算得出的距离散布远小于小口径弹道枪的原预留保险距离设计参数12～30 m，可认为在不同的弹丸初速下能够保持恒定的解除保险距离。

关键词：引信；延期解除保险；非自由式擒纵装置；周期；微机电系统(MEMS)

Citation format:ZHANG Yue-li, WANG Fa-lin.Cycle Calculation of Structure Using Centrifugal Torque to Return Based on Similar Stiffness Coefficient[J].Journal of Ordnance Equipment Engineering,2016(3):151-154.

随着微机电技术(MEMS)的发展，国内从2005年开始对引信用保险机构[1]进行微小型化改进设计。传统的钟表游丝类的结构类型在经过准LIGA工艺平面化结构改进后，结构形式[2]发生极大变化，无法验证其性能优劣，所以对在微尺度条件下轮系结构设计及周期时间评估提出了新的课题。

利用离心力矩返回的非自由式擒纵装置就是在微尺度条件下的一个应用实例。该结构通过改变平衡摆的形状，利用平衡摆质心与平衡摆转轴不重合，在离心环境下产生类似于游丝作用的力矩，同时满足准LIGA加工工艺[3]要求的平面结构，实现了在微尺度条件下的应用。虽然该结构是在传统非自由式擒纵装置[4]的基础上进行的设计改进，但由于结构中没有游丝，没有了传统轮系中的游丝刚度等参数概念，无法借用现有公式验证，也就不能对其特性具体分析。针对此情况，本研究提出了“类刚度系数”的概念，并据此使用传统非自由式擒纵装置周期公式计算了该机构的平衡摆振动周期。

1基础

1.1传统非自由式擒纵装置的结构特点

从GJB135—2002《引信工程设计手册》[4]可知，传统的非自由式擒纵装置(见图1)是传统的三维结构，非常复杂，通过调整游丝的长度可以实现振动周期的调整。其轮系结构中采用的平衡摆，由于传统加工手段所产生的误差相对较大，一致性较差，所以一般情况下为了避免钟表走时受弹道环境影响，要求平衡摆的质心与平衡摆轴心重合，并放置于弹丸的轴心位置，在游丝作用下实现等时效应。但引信延期解除保险机构并不希望返回力矩恒定，反而希望振动周期随驱动力变化，呈现对加速度的重积分效果，实现解除保险距离恒定[5]。

1.平衡摆； 2.摆轴； 3.游丝； 4.挡板； 5.滑块螺钉；

1.2传统非自由式擒纵装置的主要计算公式

《引信工程设计手册》中提到，游丝的刚度就是变形—弧度所需要的力矩，并根据《机械设计手册》[6]进行推导验证，游丝的刚度系数为力矩与转角的比值

(1)

式中：m0为游丝产生的扭矩(N·m)；θ为变形后的游丝与平衡位置形成的夹角(rad)；C为游丝刚度。

另外，传统的非自由式擒纵装置的周期计算公式

(2)

式中：T为非自由式擒纵装置中平衡摆的自由振动周期(s)；Jb为平衡摆的转动惯量(kg·m2)；C为游丝刚度。

1.3离心力矩返回的擒纵装置与传统非自由式擒纵装置结构对比

微尺度下利用离心力矩返回的非自由式擒纵装置(见图2)属于平面结构，平衡摆的轴心与其质心位置不重合。所以，在力学环境下平衡摆的运动过程类似于单摆的运动，当平衡摆质心不处于其平衡面时，产生一个拉向平衡面的力矩，通过借用单摆往返运动替换了游丝类型系统中的反复振动过程，实现微尺度平面结构条件下的应用。由于返回力矩的来源与游丝不同，产生类似传统钟表轮系游丝结构振动过程的刚度特性，所以，这里定义为“类刚度系数”，应用于计算轮系结构周期。

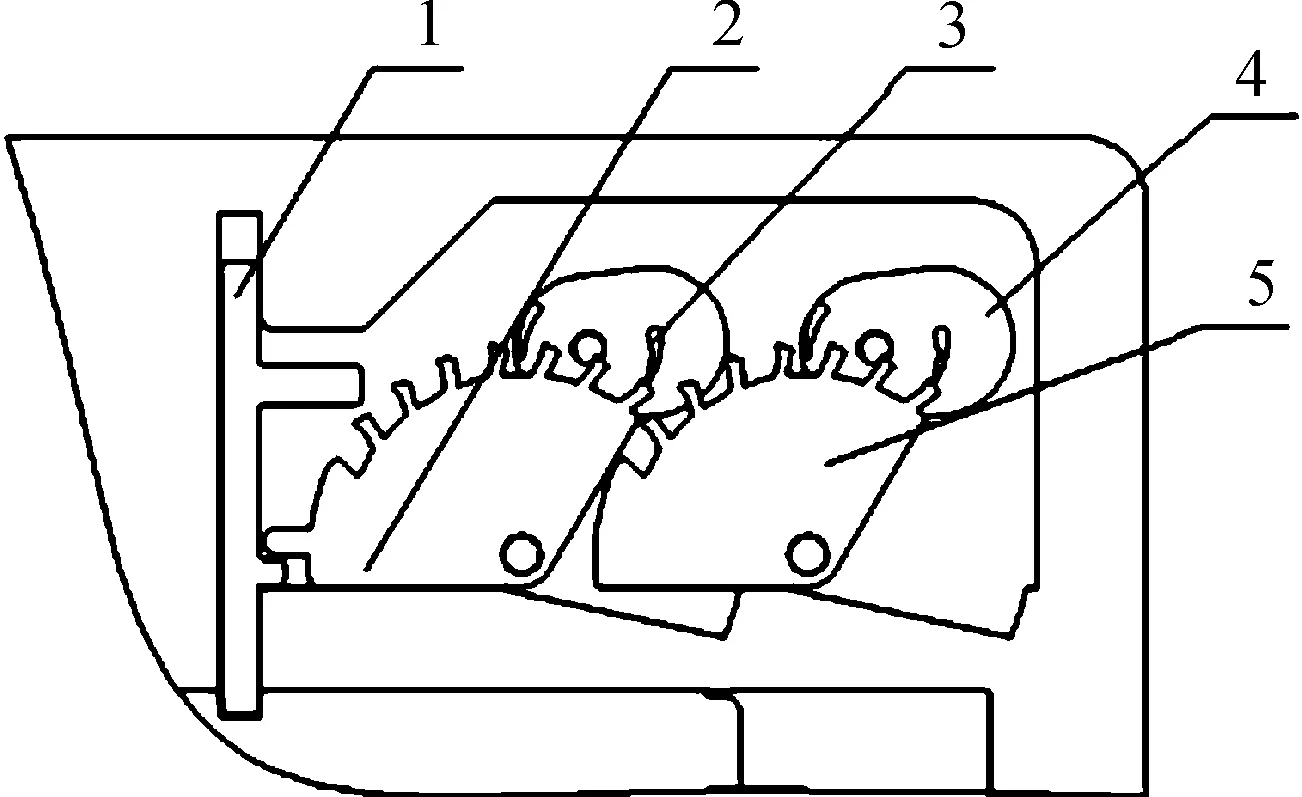
1.卡销; 2.齿轮卡板1; 3.平衡摆1; 4.平衡摆2; 5.齿轮卡板2

2利用离心力矩返回的非自由式擒纵装置周期

2.1类刚度系数

离心力矩返回的擒纵装置的啮合参数全部与传统非自由式擒纵装置相同，其啮合过程也与传统钟表轮系的啮合过程相似，因此，可以用式(2)计算周期。但由于没有游丝，没有游丝刚度系数。

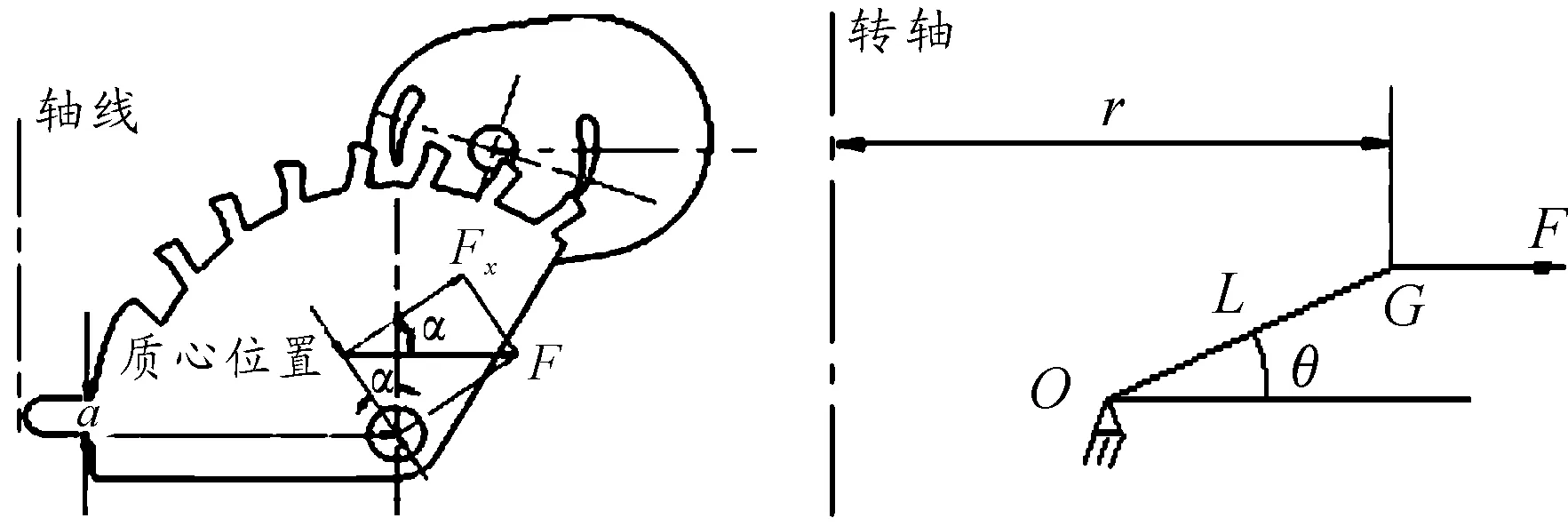
图3　微尺度条件下利用离心力矩返回的偏心平衡

根据刚度系数的定义，即在离心力下产生的力矩—转角的一个数值，假设利用离心力矩返回的偏心平衡摆亦存在类似游丝刚度的一个参数C＇，这里简称为“类刚度系数”，那么有

(3)

式中：C＇为“类刚度系数”(N·m/rad)；θ为平衡摆的转角(rad)；m0为离心力对平衡摆产生的力矩(N·m)。

另外，根据图3进行分析，可得到平衡摆受离心力作用的力矩为

m0=FLsinθ

(4)

式中：F为受弹丸旋转影响平衡摆受到的离心力(N)；L为偏心平衡摆上质心位置G点到平衡摆转动轴心O点之间的距离(m)；θ为平衡摆的转角(rad)；m0为离心力对平衡摆产生的力矩(N·m)。

由于平衡摆转角范围较小，取近似θ=sinθ，得出

(5)

根据式(3)，调整式(5)，可得“类刚度系数”

(6)

根据离心力F=mrw2计算公式，而w利用弹道环境转速替换，可代入得“类刚度系数”

(7)

式中：m为平衡摆的质量(kg)；n为弹丸转速(r/min)；r为平衡摆质心到弹丸旋转轴心的距离(m)；L为偏心平衡摆上质心位置G点到平衡摆转动轴心O点之间的距离(m)。

2.2利用离心力矩返回的非自由式擒纵装置平衡摆的周期

将式(7)代入式(2)，得到一个由常见弹道系数和平衡摆几何参数组成的周期公式

(8)

由式(8)可知，微尺度条件下利用离心力矩返回的偏心平衡摆的振动周期除了与弹丸转速和引信中平衡摆所处的位置有关，还与平衡摆的物理特性有关。

2.3解除保险距离不受弹丸初速散布影响

假设弹丸速度不衰减，偏心平衡摆经过N个周期的转动，弹丸可靠解除保险，则保险距离S为

(9)

定义膛线的缠度为K，将式(8)代入式(9)，得

(10)

根据式(10)的推导可以看出，利用离心力矩返回的非自由式擒纵装置的解除保险距离不受弹丸速度及转速的影响，只与发射器的缠度(K)、引信中平衡摆所处的位置(r)、平衡摆自身的结构(L)及特性参数(m、Jb)有关。所以，利用离心力矩返回的非自由式擒纵装置的振动周期随驱动力发生变化，呈现出对加速度的重积分效果，理论上可实现解除保险距离恒定。

3仿真计算

3.1周期仿真计算

通过实施例对微尺度条件下利用离心力矩返回的偏心平衡摆的振动周期[7]公式进行周期仿真计算。

根据平衡摆设计参数(见表1)，可得振动周期T为

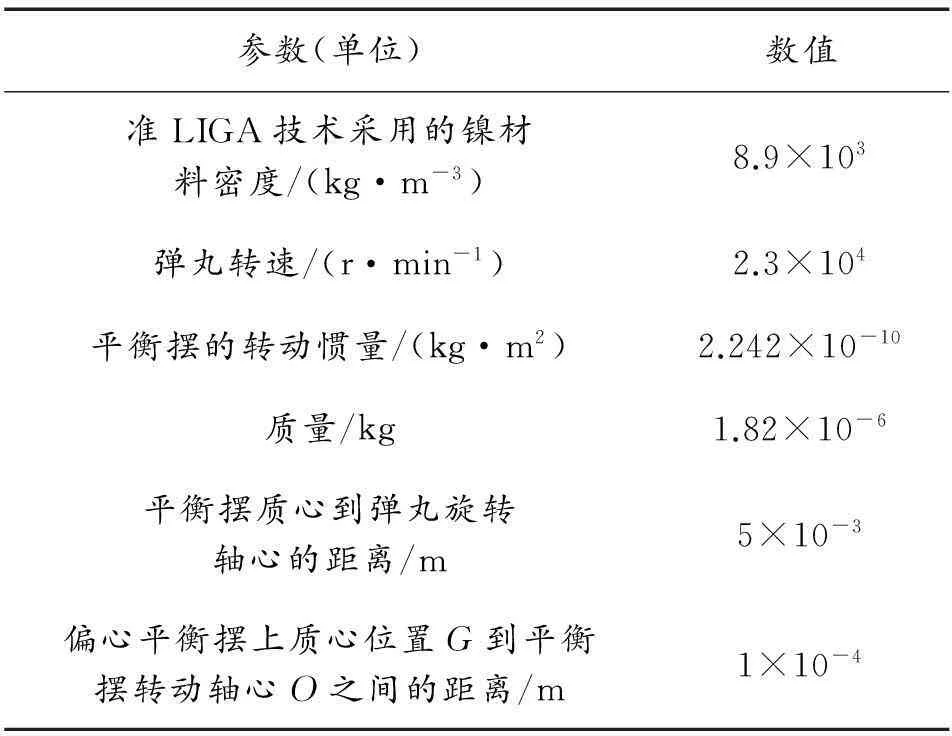
表1　偏心平衡摆参数

在ADMAS软件下建立偏心平衡摆仿真模型，根据参数表设定参数，弹轴轴心到平衡摆质心位置的距离为5 mm，借用小口径弹药转速(2.3×104r/min)，建立恒定的离心力场，取仿真时间为(End time)0.1 s，仿真步长为(Step size)10 μs进行模拟仿真计算。

得到图4所示仿真曲线，其中Part3为第一组振动系统的振动过程，Part2为第二组振动系统的振动过程，振动过程均匀有序，说明微尺度下利用离心力矩返回的非自由式擒纵装置机构运行平稳。机构保险时间大约83 ms，满足引信对远解时间的要求。

根据仿真曲线数据截取4个振动周期并平均计算，得出平衡摆的振动周期为7.63 ms，相对计算周期的误差为4.5%。

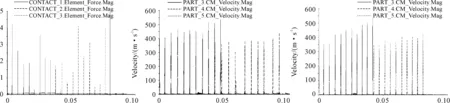
图4　仿真验证曲线

3.2恒定的解除保险距离仿真计算

用小口径弹道枪膛线的缠度为0.5、出炮口速度为190 m/s的弹道参数进行计算，根据保险距离计算公式可知，若不同速度弹丸在利用离心力矩返回的非自由式擒纵装置的延期时间内飞行的距离一致，则解除保险距离保持恒定。

假设弹丸的速度散布分别为-10%、-5%、+5%、+10%，分别得到出炮口的弹丸速度为171 m/s、180.5 m/s、199.5 m/s、209 m/s。在周期仿真模型的基础上，根据实际弹道参数调整模拟离心力的惯性力，分别求取弹丸转速为2.07×104r/min(-10%)、2.185×104r/min(-5%)、2.415×104r/min(+5%)、2.53×104r/min(+10%)，进行单组平衡摆仿真计算，得到图5所示曲线。

在图5中，去除首尾各半个周期，分别截取中间4个振动周期平均计算，可得出平衡摆的振动周期分别为8.4 ms、8 ms、7.25 ms、6.87 ms。

利用式(9)对保险距离进行计算，可得理论计算的保险距离分别为13.6 m、13.7 m、13.7 m、13.6 m，对实施例进行计算可得13.7 m。而根据经验可知，弹丸出炮口后有段后效期，所以实际的保险距离大约在16～17 m，散布很小。

利用离心力矩返回的非自由式擒纵装置经过仿真计算得出的距离散布，远小于小口径弹道枪的原预留保险距离设计参数12～30 m，可认为其在不同的弹丸初速下能够保持恒定的解除保险距离。

图5　调整模拟离心力的惯性力参数得到的仿真验证曲线

4试验情况

该性能试验在轻武器引信产品项目研制过程中进行验证(见图6)。由于目前对轻武器引信的炮口保险距离和解除保险距离要求依然为12 m和30 m，首先针对该指标进行验证。利用改装引信，用弹道枪对12 m固定立靶进行10发炮口保险距离试验，10发被试品在15 m处隔爆板处于安全隔离状态；对50 m固定立靶进行10发解除保险距离试验，10发被试品在30 m处隔爆板处于爆炸序列对正状态。然后通过前移保险距离立靶和后移解除保险距离立靶，循环试验验证，测得16～18 m为机构的解除保险距离范围。

由于弹道枪发射过程中的初速散布较大，试验结果证明保险机构的解除保险距离恒定。

图6　用于试验的保险机构产品及立靶靶板

5结论

本研究针对利用离心力矩返回的非自由式擒纵装置无法借用现有公式进行设计计算的情况，提出了“类刚度系数”的概念，类刚度系数与转速平方、摆的质量、摆质心对摆轴的偏心距离、对弹轴的偏心距离成正比，以类刚度系数带入传统非自由式擒纵装置周期公式计算了该机构的平衡摆振动周期。该结构的振动周期能够随驱动力发生变化，实现解除保险距离恒定。通过仿真计算得到的振动周期与试验数据基本一致，证明提出的“类刚度系数”的概念合理，同时经过仿真计算得出的距离散布远小于小口径弹道枪的原预留保险距离设计参数12～30m，可认为其在不同的弹丸初速下能够保持恒定的解除保险距离。

参考文献：

[1]石庚辰，李华.引信MEMS远距离解除保险机构[J].探测与控制学报，2008(3):1-4.

[2]郝永平，吴小芙，刘双杰，等.基于MEMS的钟表惯性延时机构仿真分析[J].沈阳理工大学学报，2009,28(6):1-4.

[3]李华，石庚辰.基于LIGA工艺的横向变形MEMS定位机构设计[J].纳米技术与精密工程，2007(5):289-292.

[4]总装备部军标出版发行部.引信工程设计手册[M].北京：国防工业出版社,1978.

[5]彭长清.时间引信设计[M].北京：国防工业出版社，1988.

[6]机械设计手册编委会.机械设计手册[M].2版.北京:机械工业出版社,2002.

[7]李华，王华，焦国太.引信延期解除保险机构设计与动态仿真研究[J].华北工学院学报，2004(1):31-34.

(责任编辑唐定国)

Cycle Calculation of Structure Using Centrifugal Torque to Return Based on Similar Stiffness Coefficient

ZHANG Yue-li, WANG Fa-lin

(Xi’an Institute of Electromechanical Information Technology, Xi’an 710065, China)

Abstract:Aiming at of the balance of the struture that the micro-scale conditions non-freestyle escapement device that uses centrifugal torque to return is lack of theoretical calculation basis, the concept of “similar stiffness coefficient” was put forward, and the vibration cycle of balanced pendulum was calculated with traditional non-freestyle escapement device cycle formula. The vibration cycle of the balance of the structure changed with the driving force, and the arming distance is constant. The cycle calculated through the formula are the same as experimental data basically. The concept of “similar stiffness coefficient” is reasonable. At the same time, scattered distance through the simulation was far less than design parameters of original reservation safety distance from 12 meters to 30 meters of the small bore bullet. It was considered to be able to maintaining a constant arming distance in different projectile velocity.

Key words:fuze; delayed arming distance; non-freestyle escapement device; cycle; Microelectromechanical System(MEMS)

文章编号：1006-0707(2016)03-0151-05

中图分类号：TJ43；TN405

文献标识码：A

doi:10.11809/scbgxb2016.03.036

作者简介：张跃丽(1980—)，女，工程师，主要从事引信总体结构设计研究。

收稿日期：2015-09-07；修回日期：2015-09-27

本文引用格式：张跃丽，王发林.基于类刚度系数的离心力矩返回机构周期计算[J].兵器装备工程学报，2016(3):151-154.

【机械制造与检测技术】