启发式伏格尔法求解多阶段决策问题
孙鹏飞,刘建永
(解放军理工大学 野战工程学院,南京 210007)
启发式伏格尔法求解多阶段决策问题
孙鹏飞,刘建永
(解放军理工大学 野战工程学院,南京210007)
摘要:针对动态规划求解多阶段决策问题存在的一些不足,首次创新性地将启发式伏格尔法运用到求解多阶段决策问题中,给出相关定义,列出其算法步骤,并分析其时间复杂度;通过案例具体说明启发式伏格尔法求解过程,总结该算法优缺点,为研究多阶段决策问题提供一种新型并且具有实效的思路方法。
关键词:启发式伏格尔法;时间复杂度;多阶段决策问题
Citation format:SUN Peng-fei,LIU Jian-yong.Heuristic Vogel Method for Solving Multistage Decision-Making Problems [J].Journal of Ordnance Equipment Engineering,2016(3):171-174.
求解多阶段决策问题(Multistage Decision-Making Problems),最常用的求解方法是动态规划(Dynamic Programming)方法[1-2]。实践也证明了求解此类问题用动态规划方法比线性规划方法或非线性规划方法更加有效[3-4]。但利用动态规划求解多阶段决策问题,存在着一些条件限制,算法复杂度也较大,并且只适用维数相对较低的问题[5-6]。现实中,在考虑决策灵活机动和方案最优时,并不一定要严格采用最优方案,有时决策容易、易于改动的次优方案可能更适合现实需求。本文中考虑是否有较好的启发式算法(Heuristic Algorithm)[7],在解决此类问题时更加地灵活机动、易于操作。
查阅国内外文献资料[8-10],伏格尔法(Vogel)主要应用于求解运输问题和指派问题,目前还未有关于伏格尔法在求解多阶段决策问题方面的相关研究。本文探索利用启发式伏格尔法(Heuristic Vogel Method,HVM)求解多阶段决策问题,并分析其时间复杂度。
1基于启发式伏格尔法求解最短路线问题
1.1启发式伏格尔法基本概念
伏格尔法主要应用于运输问题求解最低运费,它是确定运输问题初始调运方案中近似程度最好的一种近似方法,这种方法得出的结果很接近最优调运方案。伏格尔法在最小元素的基础上考虑,某一产地的产品若不能按照最小运费就近供应,就考虑次小运费,这就产生一个差额,称为罚金成本。罚金成本越大,说明不按最小运费调运时,运费增加越多。因而对罚金成本最大元素,就应该采用最小运费调运[1]。
启发式伏格尔法(HVM)可以定义:在可接受的花费(指计算时间和空间)条件下,给出待解决的组合优化问题一个经验构造或直观性伏格尔法求解,该可行解与最优解的偏离程度不一定事先可以预计[7]。
1.2启发式伏格尔法算法步骤
假设每阶段所有的状态点与随后阶段的状态点间均有路线,如若没有路线,可假定其路线长度为∞,过程只有一个始点Os和一个终点Oe。
启发式伏格尔法求解最短路线问题的算法步骤如下:
第1步,确定过程的始点Os、终点Oe、阶段数n、状态总数N,按始点Os至终点Oe顺序,为每个状态点排序,并确定第i状态属于哪个阶段以及该状态的决策数目mi;
第2步,计算各个状态点的决策集中最小值与次最小值的差ci(如若状态点只有一种决策,即不存在次最小值,则规定其罚金成本为0;若状态点没有决策,则不将其计入集合C中),形成集合C;
第3步,在集合C中找出最大值,并选择此状态点为决策点(如若存在多个最大值,则只选取按照状态点的排序顺序最靠前的依次作为决策点),选取此状态点的决策集中的最小值作为此状态点的决策;
第4步,从此阶段及下阶段中,除去此次决策的起、始状态点外的其余状态点,从集合C中除去此次决策的起、始状态点,更新集合C;
第5步,重复第2、4步工作,直至集合C不再包含任何状态点的罚金成本,则所有阶段中均有且仅有一个状态已做出决策,形成最终策略。
1.3启发式伏格尔法时间复杂度
算法第1步主要判断过程及状态,时间复杂度为1。
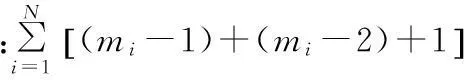
算法第3步时间复杂度计算包括寻找最大值以及为该状态点做出决策、形成阶段路线两个方面,时间复杂度:(N-1)+1。


2实例应用
2.1实际案例
某工厂自国外进口一部精密机器,由机器制造厂到出口港有3个港口可供选择,而进口港又有3个可供选择,进口后可经由两个城市到达目的地,其间的运输成本如图1中所标数字,求出运费最低的路线。

图1 路线网络图
2.2启发式伏格尔法求解
根据网络图以及启发式伏格尔法算法步骤,可以确定过程的始点为A,终点为E,共有4个阶段,10个状态点。为10个状态点依次排序,如对状态点B1,i=2。
第二步,计算各个状态点的决策集中最小值与次最小值的差。如对状态点B1,B1共有3条可选路线,其中最小值为40(路线B1→C2),次最小值为60(路线B1→C3),二者之差,即c2=20。求出每个状态点的最小值与次最小值之差,形成集合C,初始的集合C中一共包括[A、B1、B2、B3、C1、C2、C3、D1、D2]这9个状态点的罚金成本。如图2中各状态点上的括号内数值所示:

图2 初始集合C
从集合C中找出最大值,B3、C1、C23个状态点的最大值,均为30。按照本文的算法规则,选择序号在前的状态点B3作为决策点,并将状态点B3的3条可选路线中最短路线B3→C2作为该阶段路线,如图3所示。
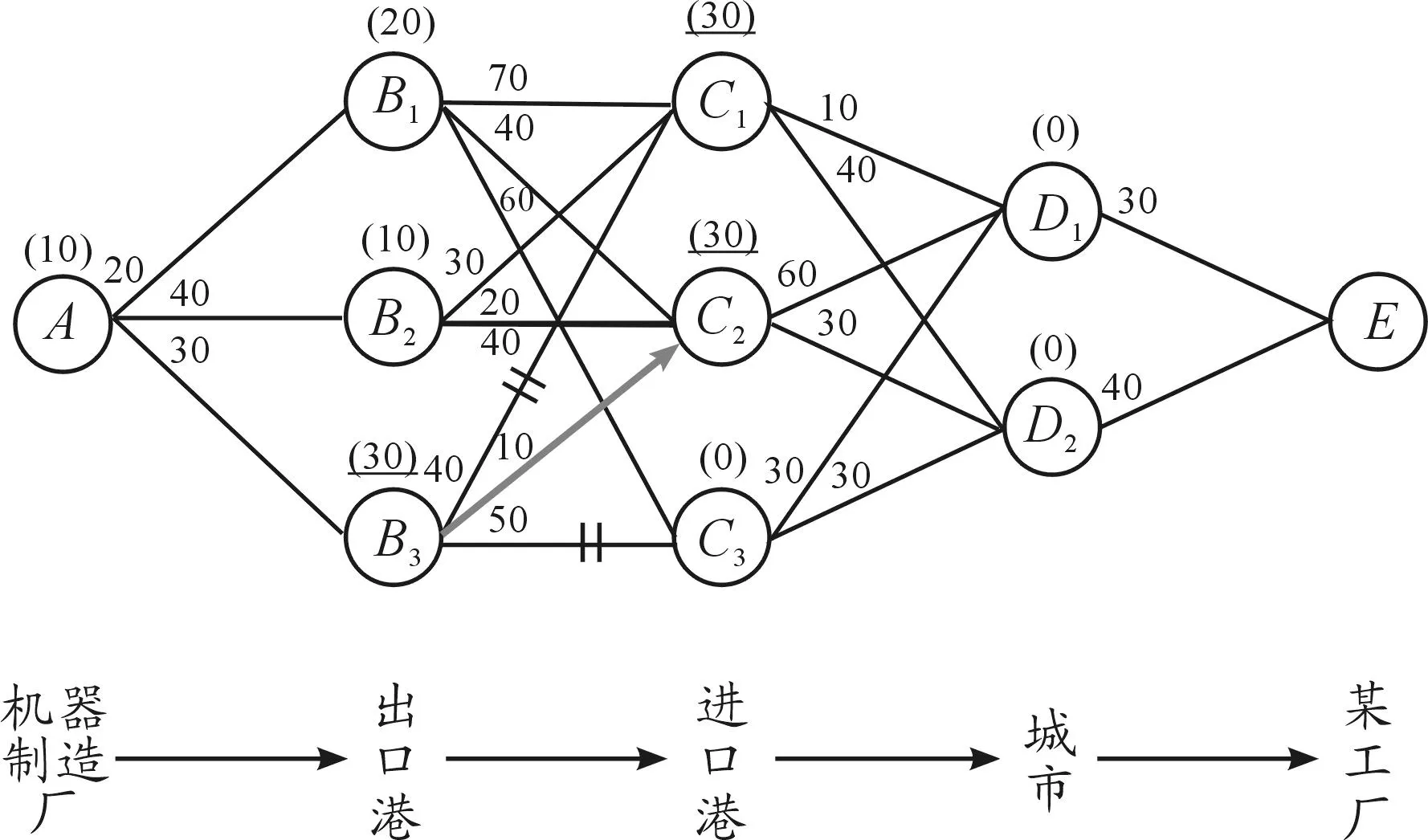
图3 状态B3作为首选点

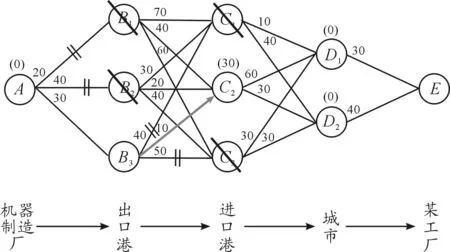
图4 更新后的集合C

图5 路线C2→D2的选择



图6 路线A→B3的选择
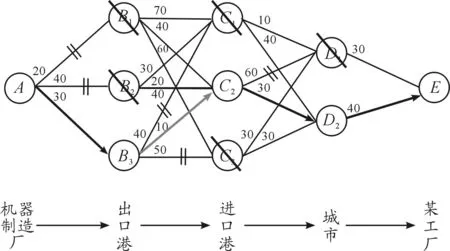
图7 路线D2→E的选择
从集合C中除去此次决策的起始状态点D,更新后的集合C中不再包含任何状态点的罚金成本,即所有阶段均有且仅有一个状态已做出决策, 完成了此过程路线的确定策略。最后得到路线方案:
A→B3→C2→D2→E
2.3结果分析
启发式伏格尔法方案的路线运输成本为110,利用动态规划方法求解进行验证(具体求解过程未在本文列出),110为最优结果。
由此总结出启发式伏格尔法求解的特点:求解结果清晰明了,图上标示直观方便;阶段越多或状态决策数目越多时,越是后面的求解过程中,越能体现出其计算时间优越性。与动态规划求解多阶段决策问题的按顺序或反序逐个阶段进行决策,最后得出从全局出现的最优决策相比,本方法并不能保证从两端逐个阶段进行,而是选取罚金成本最大值的状态点开始,而此状态点可能处于中间某个状态,所以不能保证每次都能求出最优决策,而且无法直观验证其结果是否为最佳方案。
3结论
本文将启发式伏格尔法思想应用到求解多阶段决策问题中,方法简便,理论可靠,而且结果清晰明了,研究前景开阔,在实际运用中取得了良好效果。本文实例比较简单,在实际中有可能存在多个始、终点的情况,或是状态不满足无后效性的情况,在这些特殊情况下,本算法可能会得到很坏的答案或效率极差,这就违背了算法初衷。
本文下一步工作将在两方面展开深入研究,一是对该算法求解的实效性以及算法复杂度进行研究,改善优化算法;二是完善规范算法步骤,实现算法计算机编程,使其达到在较为复杂的情况下,也能满足在计算机运行的准确性和稳定性。
参考文献:
[1]钱颂迪.运筹学[M].3版.北京:清华大学出版社,2005.
[2]BELLMAN R E,DREYFUS S E.Applied Dynamic Programming[M].Princeton University Press,1962.
[3]SVEN D.Nonlinear and Dynamic Programming[M].Springer-Verlag,1975.
[4]KUMAR P,SINGH N,TEWARI N K.A nonlinear goal programming model for multistage,multiobjective decision problems with application to grouping and loading problem in a flexible manufacturing system[J].European Journal of Operational Research,1991,53(2):166-171.
[5]YANG MAO,LI YONG,SU LI.Opportunistic spectrum sharing in software defined wireless network[J].Journal of Systems Engineering and Electronics,2014,25(6):934-941.
[6]LI YONG-YAN,GAO WEN,WU CHUNMING.Deployment of Sensors in WSN:An Efficient Approach Based on Dynamic Programming[J].Chinese Journal of Electronics,2015,24(1):33-37.
[7]EDWARD A,SILVER,VICTOR R.A tutorial on heuristic methods[J].European Journal of Operational Research,1980(5):153-162.
[8] 汪潘义.改进的伏格尔法及其应用[J].统计与决策,2014(15):83-85.
[9]牛斌,赵龙.基于Vogel的车辆调用优化算法研究[J].计算机与现代化,2011(5):7-10.
[10]张敏,张子杰.伏格尔法在退化性运输问题中的应用方法[J].河北工程技术高等专科学校学报,2009,12(4):21-23.
(责任编辑唐定国)
Heuristic Vogel Method for Solving Multistage Decision-Making Problems
SUN Peng-fei,LIU Jian-yong
(College of Field Engineering, PLA University of Science and Technology, Nanjing 210007, China)
Abstract:To solve the shortages appeared in the process of solving multistage decision-making problems with dynamic programming, Heuristic Vogel method was creatively applied in solving this kind of issues for the first time. Its definitions and algorithm steps were provided and its time complexity was analyzed. This paper illustrated the solving process of Heuristic Vogel method with a case, and summarized its advantages and disadvantages and provided a new and effective method for the research of solving multistage decision-making problems.
Key words:Heuristic Vogel method; time complexity; multistage decision-making problem
文章编号:1006-0707(2016)03-0171-04
中图分类号:E072
文献标识码:A
doi:10.11809/scbgxb2016.03.041
作者简介:孙鹏飞(1989—),男,主要从事指挥自动化与战场环境数字化研究。
收稿日期:2015-09-23;修回日期:2015-10-09
本文引用格式:孙鹏飞,刘建永.启发式伏格尔法求解多阶段决策问题[J].兵器装备工程学报,2016(3):171-174.
【基础理论与应用研究】

