爆炸螺栓作用同步性对弹丸着靶影响规律

张学伦，李　真，王昭明

(重庆红宇精密工业有限责任公司，重庆　402760)



爆炸螺栓作用同步性对弹丸着靶影响规律

张学伦，李真，王昭明

(重庆红宇精密工业有限责任公司，重庆402760)

摘要：针对火箭橇试验中弹丸终点弹道参数的准确性直接影响到弹丸终点效应评估的真实性，提出爆炸螺栓作用的时序及同步性对弹丸运动参量及着靶姿态的影响规律；利用CFD-FASTRAN气动力分析软件进行了数值模拟研究，分析了弹丸着靶运动参量及着靶攻角的变化关系，从中得出了爆炸螺栓作用的时序及同步性对弹丸运动参量及着靶姿态的影响规律；结果表明：爆炸螺栓作用时序及同步性对弹丸的运动参量及着靶姿态的影响较小。

关键词：爆炸螺栓；同步性；弹丸；着靶参量；火箭橇试验

Citation format:ZHANG Xue-lun，LI Zhen，WANG Zhao-ming.Influence of Explosive Bolts’ Synchronization on Projectile Impact Attitude [J].Journal of Ordnance Equipment Engineering,2016(3):23-26.

弹丸终点弹道参数的准确性直接影响到弹丸终点效应评估的真实性。因此，保障弹丸的终点弹道参数是评估弹丸终点毁伤效应的前提。

在地面弹丸终点效应考核试验中，火箭橇试验法[1]是目前较为常用的方法。火箭橇试验技术中，采用爆炸螺栓实现弹与橇车的分离，即被试弹丸通过前、后两道压环固定，压环两侧通过爆炸螺栓沿竖向固定在橇车立柱上。火箭橇运行到预定位置时，爆炸螺栓通电作用，释放固定弹丸的压环，弹丸按照规定的终点弹道运动参量自由飞向目标，实现对弹丸终点毁伤效应的打击。由于弹丸与橇车分离技术本身的复杂性，对其影响分离的干扰因素认识不够深入，常常导致试验结果与预设结果偏离。夏洪利[2]等进行了战斗部终点效应着靶攻角控制技术的研究，但未涉及爆炸螺栓作用时序及同步性对弹丸终点运动参量及姿态参量的研究。

文中利用CFD-FASTRAN气动力分析软件对某型弹丸着靶运动参量、姿态参量进行了数值模拟分析，主要从弹丸终点运动时间、质心运动轨迹、速度变化及攻角变化的方面考察了爆炸螺栓作用时序及作用同步性等因素的变化对弹丸终点参量的影响。

1数值模拟计算模型

1.1计算基本假设

计算模型的建立基于以下假设：不考虑结构卡环的变形及分离瞬间的结构相互干扰；不计撬车对弹丸的气动干扰；不考虑卡环释放过程中对弹丸的干涉；忽略弹丸与结构连接间的摩擦力。

1.2模型及坐标系

计算过程中涉及两个坐标系，即地面坐标系OXYZ和弹丸自身坐标系O1X1Y1Z1。弹丸被释放的初始时刻，弹丸自身坐标系O1X1Y1Z1相对地面坐标系OXYZ在绕Z轴方向预置2°夹角，飞行过程中弹丸相对地面坐标系运动。

地面坐标系OXYZ是与地球表面固连的坐标系，坐标原点O在发射瞬时弹丸的质心上，OX轴为弹道面与水平面交线，指向目标为正，OY轴沿垂线向上，OZ轴与其他两轴垂直并构成右手坐标系[3]。

弹丸自身坐标系采用弹体坐标系，原点O1在质心上；O1X1轴与弹丸纵轴重合指向头部为正；O1Y1轴位于弹丸纵向对称面内与O1X1轴垂直，指向上为正；O1Z1轴垂直于O1X1Y1平面，方向按右手直接坐标系确定。图1为弹丸坐标系及约束示意图。

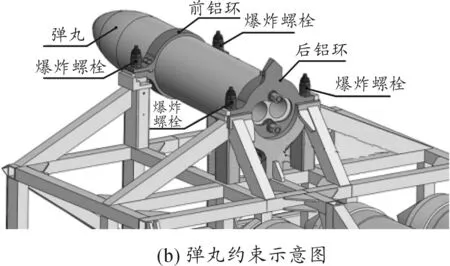
图1　弹丸坐标系及约束示意图

1.3控制方程[4]

根据弹丸约束情况，建立弹丸自身坐标系相对地面坐标系的六自由度运动方程如下：

1.4计算方法及参数

计算中湍流模型选择S-A湍流模型，采用标准大气参数。弹丸初始攻角预置为2°、初始速度预设为860 m/s，设置爆炸螺栓作用时刻点到着靶点的距离为21 m。爆炸螺栓作用时序及同步性分别设置为以下3种工况：

工况1：前、后爆炸螺栓同时作用，相当于弹丸从始至终处于自由飞的状态，不需要添加约束。

工况2：前端爆炸螺栓比后端爆炸螺栓先作用4 ms的情况，在后爆炸螺栓处添加铰链约束，约束生效时间为0～4 ms，4 ms后战斗部处于自由飞状态。

工况3：前端爆炸螺栓比后端爆炸螺栓后作用4 ms的情况，在前爆炸螺栓处添加铰链约束，约束生效时间为0～4 ms，4 ms后弹丸处于自由飞状态。

计算时先进行一定次数稳态计算，然后分别加载3种情况的运动模式，设置好约束条件进行3次动态过程计算[4]。

2计算结果及分析

2.1弹丸运动参数

对比3种工况对弹丸运动情况的影响，主要包括沿X方向飞行到21 m所用的时间、质心运动轨迹、速度变化等。

因弹丸初始速度高，飞行距离较短，在飞行时间上3种工况差别不大。弹丸沿X方向飞行到21 m所用的时间，工况1、工况2、工况3分别为0.024 46 s、0.024 45 s、0.024 45 s。4 ms 时刻，工况1、工况2和工况3的弹丸X方向位移为3.437 5 m、3.437 9 m和3.437 9 m。

弹丸水平方向飞行到21 m时，弹丸质心运动轨迹差别不大，工况1、工况2、工况3的Y方向位移分别为0.733 4 m、0.732 8 m、0.733 1 m。

图2和图3为分别为战斗部X方向速度和Y方向速度随X方向位移的变化关系。由图中可以看出3种工况的速度变化有所不同，引起这种现象主要原因是爆炸螺栓作用的延迟使得弹丸姿态角不同。对于工况2和工况3速度变化出现拐点的时刻即为最后一组爆炸螺栓作用时刻。

图2　X方向速度随X方向位移的变化

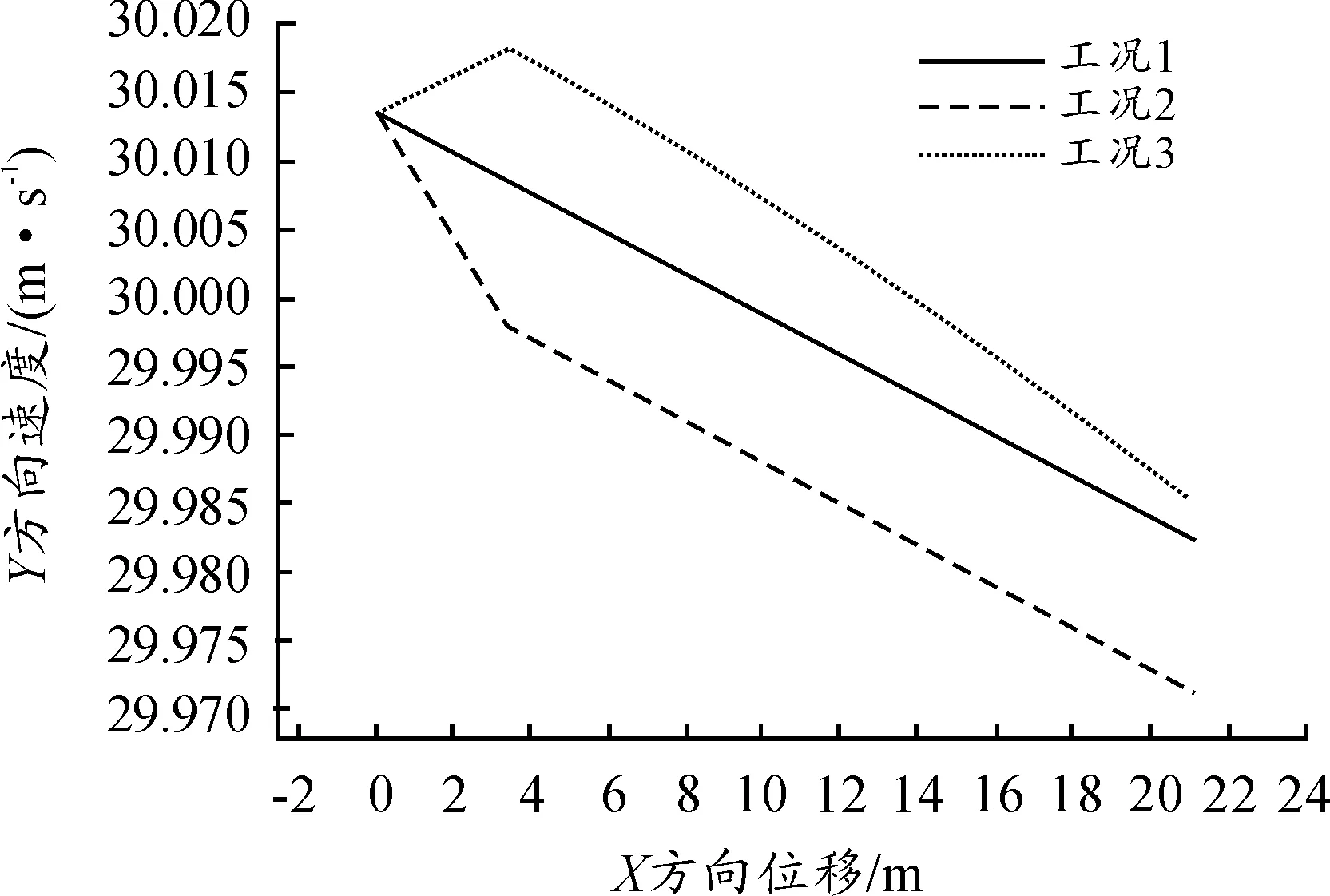
图3　Y方向速度随X方向位移的变化

工况1、工况2和工况3的X方向速度变化范围分别为[859.476 m/s，858.836 m/s]、[859.476 m/s，858.939 m/s]、[859.476 m/s，858.930 m/s]；工况1、工况2和工况3的Y方向速度变化范围分别为[30.014 m/s，29.983 m/s]、[30.014 m/s，29.971 m/s]、[30.018 m/s、29.985 m/s]。从数据上看3种工况的速度变化差距并不是很明显。

从计算结果上来看，爆炸螺栓作用的时序及同步性对弹丸运动参数的影响并不大，仅是参数的变化趋势上有略微不同。

2.2弹丸姿态角

弹丸的姿态角即弹丸自身坐标系相对于地面坐标系的姿态，图4为弹丸绕X轴、Y轴和Z轴的转动角随X方向位移的变化关系。由图中可以看出在0～4 ms内，3种工况对弹丸的姿态角有一定影响，随着飞行的继续，3种工况的姿态角差距逐渐增大。由图也可以看出3种工况弹丸绕X轴和Y轴的转动角差别很小，仅在Z轴方向差距较大，这种现象主要跟弹丸的受力情况相关。

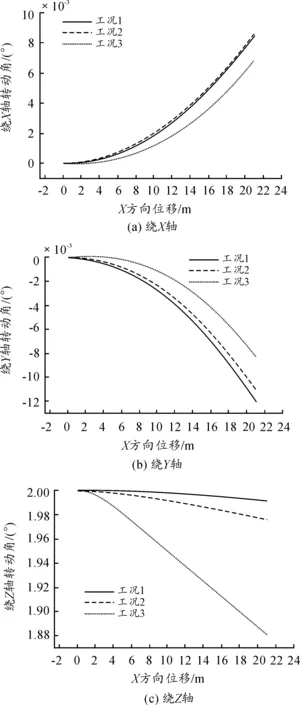
图4　转动角随X方向位移的变化

弹丸在空气中飞行时，主要受到作用在压心上的气动升力Fl、气动阻力Fd和作用在重心的重力，弹丸所受的气动力主要集中在头部曲线附近，质心在压心后，弹丸为静不稳定的，示意图见图5所示。

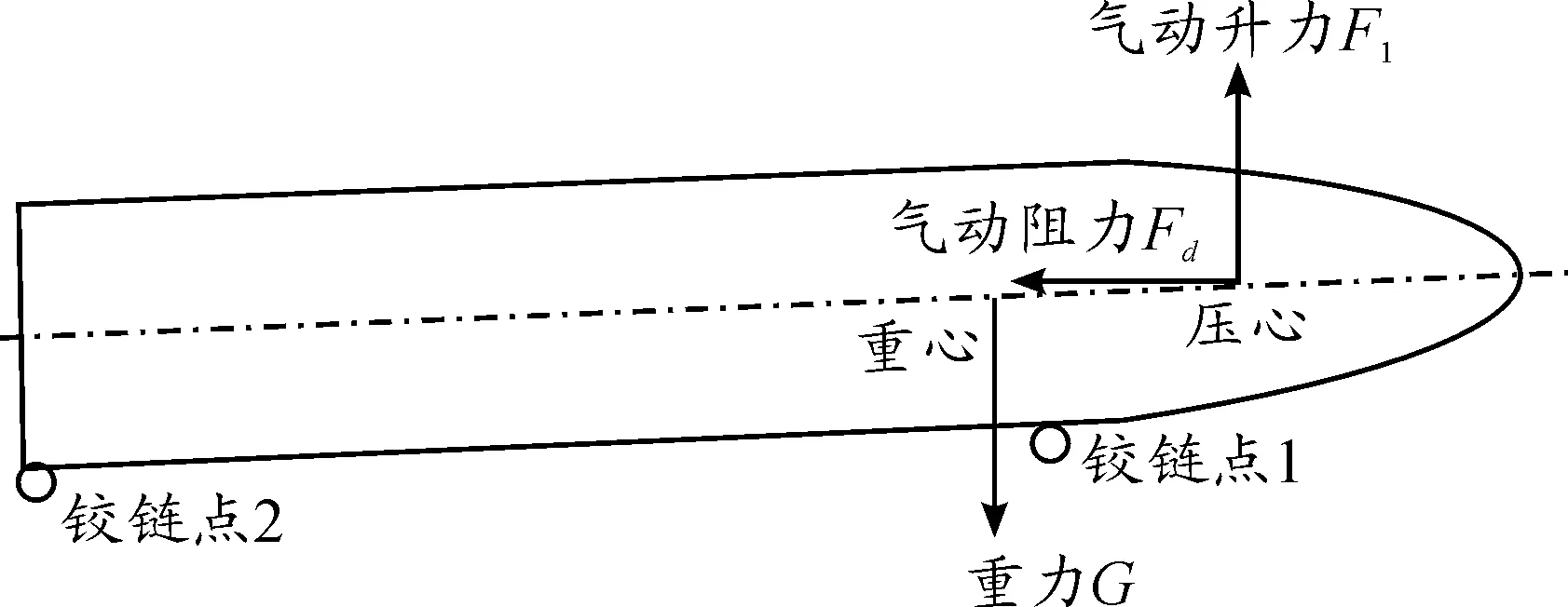
图5　弹丸受力分析示意图

工况1弹丸处于自由飞的状态，气动力足以平衡重力，平稳飞行。工况2，气动力相对铰链点2产生的力矩被重力产生的力矩抵消一部分，因弹丸为静稳定的，有自我恢复平衡的趋势，从而引起弹丸姿态的调整。工况3，气动力相对铰链点1产生的力矩和重力对铰链点1产生的力矩相互叠加，因此工况3时弹丸姿态的变化幅度比工况2的大。

从计算数据上看，3种工况绕X轴和Y轴的角度差别很小，仅绕Z轴的角度有一些差别，但总的来说差距不大。绕Z轴方向的转动角速度见表1。

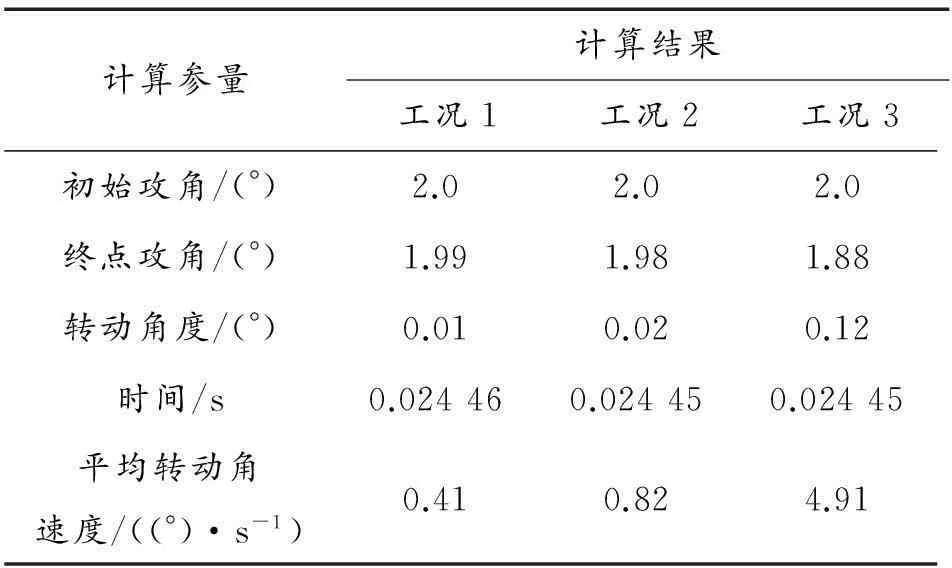
表1　绕Z轴转动角速度

从计算结果来看爆炸螺栓作用的时序及同步性对弹丸着靶姿态影响不大。本文计算爆炸螺栓作用同步性延迟时间为4 ms，而实际爆炸螺栓产品的作用同步性不会超过1 ms，因而爆炸螺栓作用的时序及同步性不是造成弹丸着靶时姿态不可控状态的主要因素。

3结论

运用CFD-FASTRAN气动力分析软件对弹丸在爆炸螺栓前后同时作用、前端爆炸螺栓比后端爆炸螺栓先作用4 ms、前端爆炸螺栓比后端爆炸螺栓后作用4 ms三种作用时序及同步性条件下弹丸着靶运动参量及姿态参量进行了数值模拟分析，得到以下结论：

1) 3种情况下，弹丸飞行时间、飞行位移、质心轨迹和飞行速度变化等，在数值上差距不大，仅在变化趋势上略有不同；

2) 3种情况对弹丸着靶姿态的影响不大，仅在绕Z轴方向的角度差别大一些，但均不会造成弹丸着靶姿态不可控。

本文在仿真过程中将弹丸的约束简化为铰链，属于一种较为极端的状态。而实际情况是爆炸螺栓作用不同步，弹丸处于一种较牢固的约束状态，仅是约束装置变形可能导致弹丸初始姿态有所变化。如果约束装置较为可靠，弹丸的初始姿态角变化幅度会比铰链状态更小，更加不会对弹丸着靶姿态造成大的影响。

参考文献：

[1]赵继波，赵峰，谭多望,等.火箭橇加载试验技术研究[J].爆炸与冲击， 2007,27(5)：572-576.

[2]夏洪利，赵卫星，党峰.战斗部终点效应火箭橇试验着靶攻角控制技术[C]//第十三届全国战斗部与毁伤技术学术交流会论文集.黄山：[出版社不详]，2013：1394-1397.

[3]钱杏芳，林瑞雄，赵亚男.导弹飞行动力学[M].北京：北京理工大学出版社，2006.

[4]ESI CFD Inc.CFD-FASTRAN V 2011.0 User Manual [M].ESI-Group,2011.

[5]王军评，毛勇建，董龙雷,等.火箭橇试验推力测量方法研究[J].振动与冲击，2013，32(18)：75-79.

[6]王健，张旭光，孔维红.火箭橇水刹车高速冲击入水安全性分析[J].南京理工大学学报(自然科学版)，2013,2013(6).

[7]刘军，李磊子.火箭橇气动阻力系数取值方法技术研究[C]//中国空气动力学会测控专业委员会六届四次空气动力测控技术交流会论文集.襄阳：[出版社不详]，2013.

[8]王超，王跃钢.火箭橇试验分离制导工具误差的有效性分析[J].中国惯性技术学报，2012，20(2).

[9]唐瑞，姚冉中.基于高速火箭橇测速系统的误差分析 [J].现代电子技术， 2015(1)：59-63.

[10]丁春全，周昊，冯志杰.火箭橇试验减振系统力学仿真研究[J].舰船电子工程，2012,32(8)：21-25.

[11]付宇，陈亚奇，仪建华，等.模拟飞行条件下固体火箭发动机内弹道性能测试技术研究[J].四川兵工学报，2015(10):36-39.

(责任编辑周江川)

Influence of Explosive Bolts’ Synchronization on Projectile Impact Attitude

ZHANG Xue-lun，LI Zhen，WANG Zhao-ming

(Chongqing Hongyu Precision Industrial Co., Ltd., Chongqing 402760, China)

Abstract:The accuracy of the rocket sled test parameters for the projectile ballistic projectile end effects directly affects the authenticity of the effectiveness assessment, and we proposed the influence law of explosive bolts timing and synchronization on parameters of projectile motion and the law of the attitude of the target; Numerial simulation study of the analysis software was proposed by using pneumatic dynamic code CFD-FASTRAN. The variation relations between projectile’s movement parameters and target attack angle were analyzed. The results show that the influence of explosive blots’ action sequence and synchronization on projectile’s movement parameters and impact attitude is negligible.

Key words:explosive bolt; synchronization; projectile; impact parameter；rocket sled test

文章编号：1006-0707(2016)03-0023-04

中图分类号：TJ55

文献标识码：A

doi:10.11809/scbgxb2016.03.006

作者简介：张学伦(1966—)，男，研究员，主要从事弹药工程研究。

收稿日期：2015-10-25；修回日期：2015-12-02

本文引用格式：张学伦，李真，王昭明.爆炸螺栓作用同步性对弹丸着靶影响规律[J].兵器装备工程学报，2016(3):23-26.

【装备理论与装备技术】