火箭飞行速度与射流冲击作用关系研究

杨　鸣，谢雨彤，王　辉，夏胜禹，王明珠

(1.四川航天系统工程研究所，成都　610100； 2.四川航天计量测试研究所，成都　610100)



火箭飞行速度与射流冲击作用关系研究

杨鸣1，谢雨彤2，王辉1，夏胜禹1，王明珠1

(1.四川航天系统工程研究所，成都610100； 2.四川航天计量测试研究所，成都610100)

摘要：通过CFD仿真分析了火箭飞行速度与射流冲击作用的关系，利用动网格技术模拟火箭不同的飞行速度；将定常计算方法和动网格方法计算结果对比，指出了两种方法的计算结果产生差异的原因并给出了特征位置选取方法；计算结果表明：不同火箭飞行速度条件下，冲击作用变化趋势基本相同但载荷峰值与飞行速度成反比；定常计算方法可以得到与动网格方法相近的结果，但如果计算的特征位置选取不当会出现较大差异；依据自由射流计算结果确定特征位置可以使两种方法计算结果较为接近。

关键词：火箭飞行速度；射流冲击；动网格；定常计算；特征位置

Citation format:YANG Ming, XIE Yu-tong, WANG Hui, et al.Research on Relationship Between Rockets Flight Velocity and Jet Impact Effect [J].Journal of Ordnance Equipment Engineering,2016(3):27-30.

火箭在发射过程中，由发动机喷射出的高温高压高速燃气射流会对发射装置产生热冲击和力冲击作用。如果结构所受冲击作用过于强烈或者自身刚强度不足就可能危及结构安全，因此确定作用于结构的射流冲击载荷变化规律对发射装置设计具有重要意义[1-3]。

火箭发射过程中与发射装置存在相对运动，计算结果中需要体现出相对位置变化所带来的影响。处理相对位置的变化有两种思路：一是利用动网格技术[4]，这种方法要求事先给出火箭运动规律或者将动力学方程与流场控制方程耦合求解。其优点是求解方法接近实际状况，得到的计算结果为时间或者路程的连续函数，便于后续分析利用。该方法的缺点是计算时间较长且处理多自由度运动问题时较为困难，而实际上火箭的俯仰、下沉对结构的冲击是有影响的[5]。另一种处理方法是将非定常问题简化为定常问题，以火箭飞行规律为基础，选取若干个特征位置，将火箭发动机布置在该位置上按定常问题计算，结合时间参数，最终得到冲击作用随时间或行程的变化规律[6-7]。该方法计算量小，可以建立火箭发动机位于多个不同位置的模型同时进行计算，从而大大提高了计算速度。另外，该方法无需考虑模型中网格的重构，可以很方便地处理火箭的不同姿态。方法的不足在于忽略了火箭速度的影响，需要考虑计算模型特征位置，否则计算结果与实际情况差异可能较大。

本文首先利用动网格技术分析了不同的火箭飞行速度对射流冲击作用的影响，再将定常计算方法和动网格方法计算结果对比，指出两者产生差异的原因并给出了特征位置选取方法。

1仿真模型的建立

基于商业CFD软件FLUENT建立分析模型，分别使用动网格方法和定常方法进行计算，动网格模型使用域动分层技术[8]。使用轴对称条件下的S-A湍流模型以简化计算规模，边界条件如图1所示，未标识边界均为压强出口条件。发动机总压随时间变化规律如图2所示，火箭发动机总温条件为3 400 K。计算过程中自动输出监控壁面最大压强和最高温度。4种使用动网格计算方案的模型火箭速度分别为10 m/s、40 m/s、80 m/s和160 m/s。

图1　计算模型边界条件

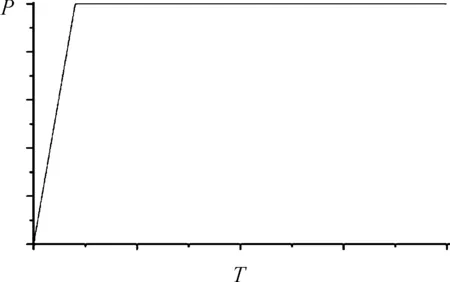
图2　发动机总压变化规律

2冲击作用受飞行速度影响分析

图3、图4为4种火箭飞行速度条件下监测壁面上所受最大压强和最高温度随火箭行程变化规律示意图。

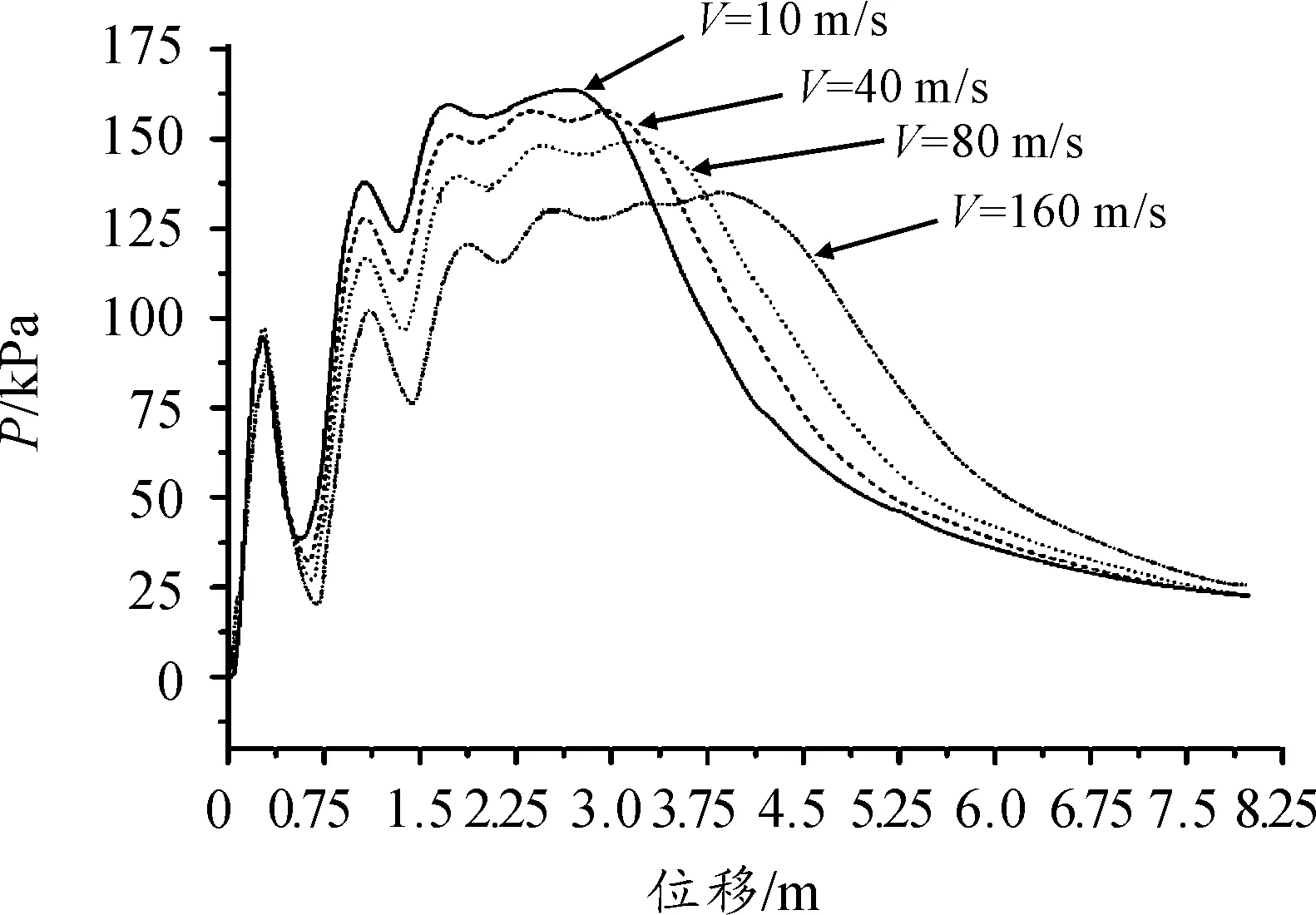
图3　最大压强随火箭行程变化规律

图4　最高温度随火箭行程变化规律

由图3和图4可知：不同火箭速度条件下，图线变化趋势基本相同，都是火箭行程小于2.5 m之前在大致相同的行程位置出现若干个波峰和波谷，之后便转入较为平滑的下降段；从计算峰值情况来看，火箭速度越快，相应的峰值越低，压强峰值和温度峰值如表1所示。

表1　压强峰值和温度峰值

3定常方法与动网格方法对比

由于定常方法是在忽略火箭速度，也就是V=0条件下的计算结果，因此火箭的实际运动速度越低则两种方法的计算结果应当越接近，因此可选取火箭速度V=10 m/s时的计算结果和定常方法计算结果作比较。按定常方法计算时，特征位置距发射箱箱口距离分别为0.04 m、0.84 m、1.64 m、2.44 m、3.24 m、4.04 m、4.84 m、5.64 m、6.44 m、7.24 m和8.00 m。图5至图6为采用定常方法和动网格技术(V=10 m/s)计算得到的最大压强和最高温度随火箭行程变化规律示意图，实心线为定常计算结果，虚线为动网格技术计算结果。

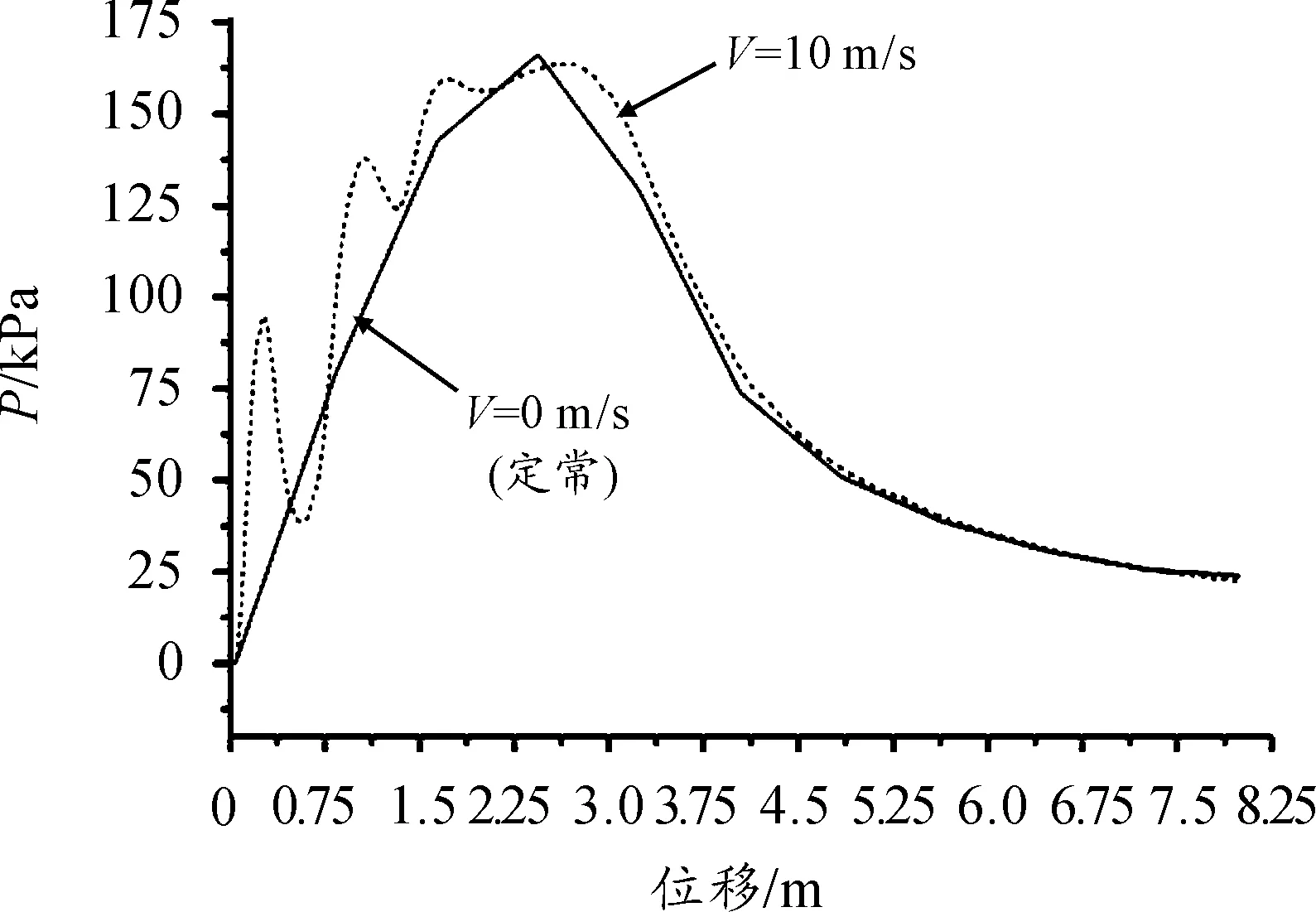
图5　两种方法得到的最大压强变化规律

图6　两种方法得到的最高温度变化规律

从图5和图6可以得到以下结论：

1) 两种方法计算得到的压强和温度峰值差别不大，图像的下降段吻合较好，上升段和下降段分界点出现在火箭行程为2.5m左右时；

2) 在图像的上升段，两种方法计算结果差别较大，定常方法的计算结果为一个单峰函数，图像上升段“波峰-波谷”交替出现的特征基本被“抹平”，温度计算结果差别尤为显著。

综上，采用定常方法计算时如果计算的特征位置选择不当将和动网格计算结果出现明显差异。

4定常方法特征位置选取分析

从第3节结论可知，要想利用定常方法得到更加准确的结果，就必须对计算位置进行有针对性的选择而不能随意选取，为此先进行冲击流场特征分析。图7为燃气冲击流场结构示意图。

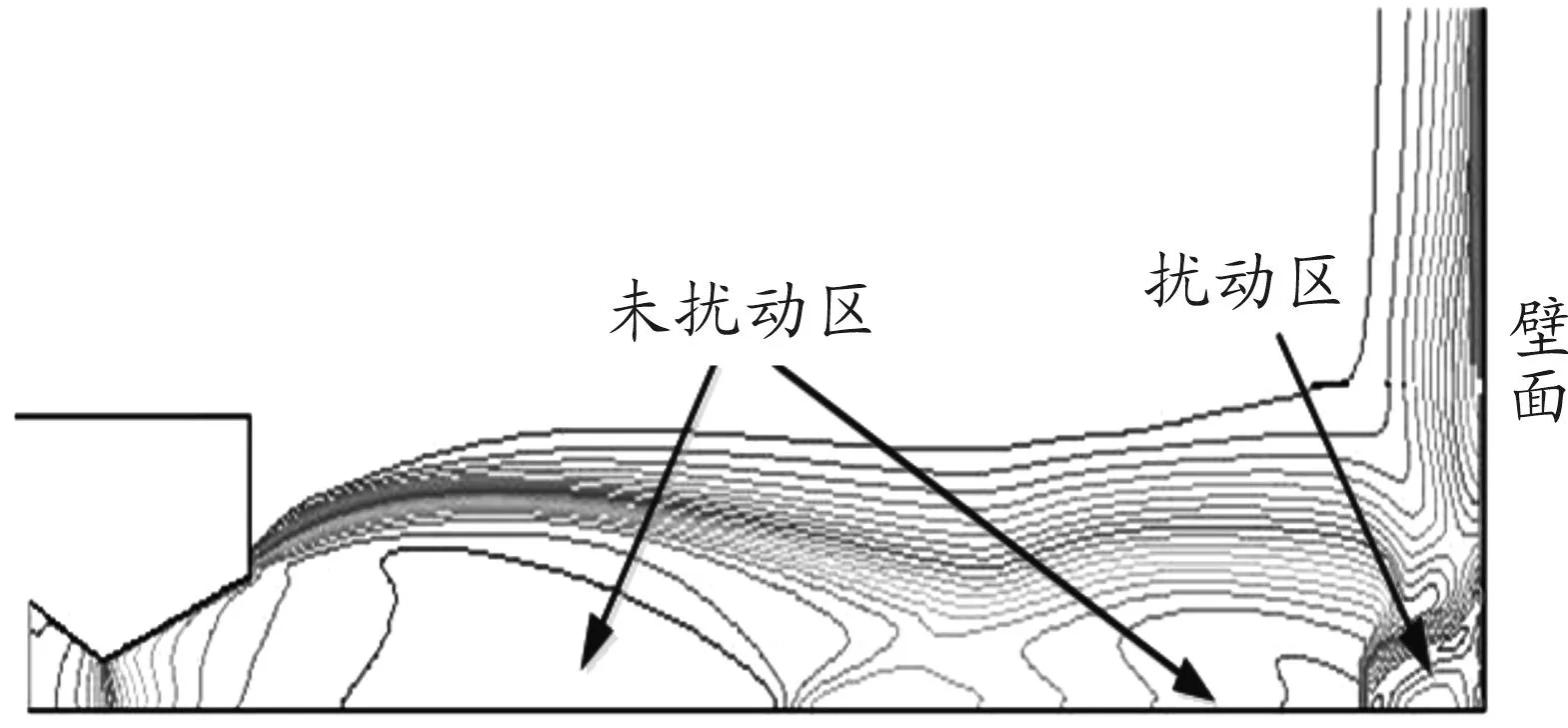
图7　燃气冲击流场结构

从图7可以看出，射流冲击流场可以看作由两部分构成，一部分形态与自由射流场结构几乎一致，可称为未扰动区；另一部分则为近壁面的扰动区，由于受壁面影响，流场结构较之自由射流场改变很大。显然，壁面受到的冲击作用和扰动区前缘的流场形态密切相关。在自由射流状态下，射流场可视作由数个波节交联构成，波节与波节交界面区域即为流场形态发生突变的位置，在该位置前后流场压强、温度、速度均发生显著变化。当交界面区域恰好位于扰动区前缘时必然引起壁面所受冲击作用的变化。因此，只要通过自由射流场计算得到各个波节交界面的准确位置，将定常计算时的特征位置选取为自由射流的整数倍波节长度，就可以改善定常计算结果，使之和按动网格方法计算得到的结果接近。

按照上述思路，先进行自由射流场计算，图8为射流轴向速度沿火箭发动机轴线分布示意图，横坐标原点取发动机出口轴线所在位置。

图8　射流轴向速度沿火箭发动机轴线分布

依据图8，重新调整定常计算特征位置距发射箱箱口距离为0.25 m、0.5 m、0.85 m、1.0 m、1.2 m、1.6 m、2.2 m、2.8 m、3.24 m、4.04 m、4.84 m、5.64 m、6.44 m、7.24 m和8.00 m。

调整后的计算结果如图9、图10所示，实心线为定常计算结果，虚线为动网格技术计算结果。

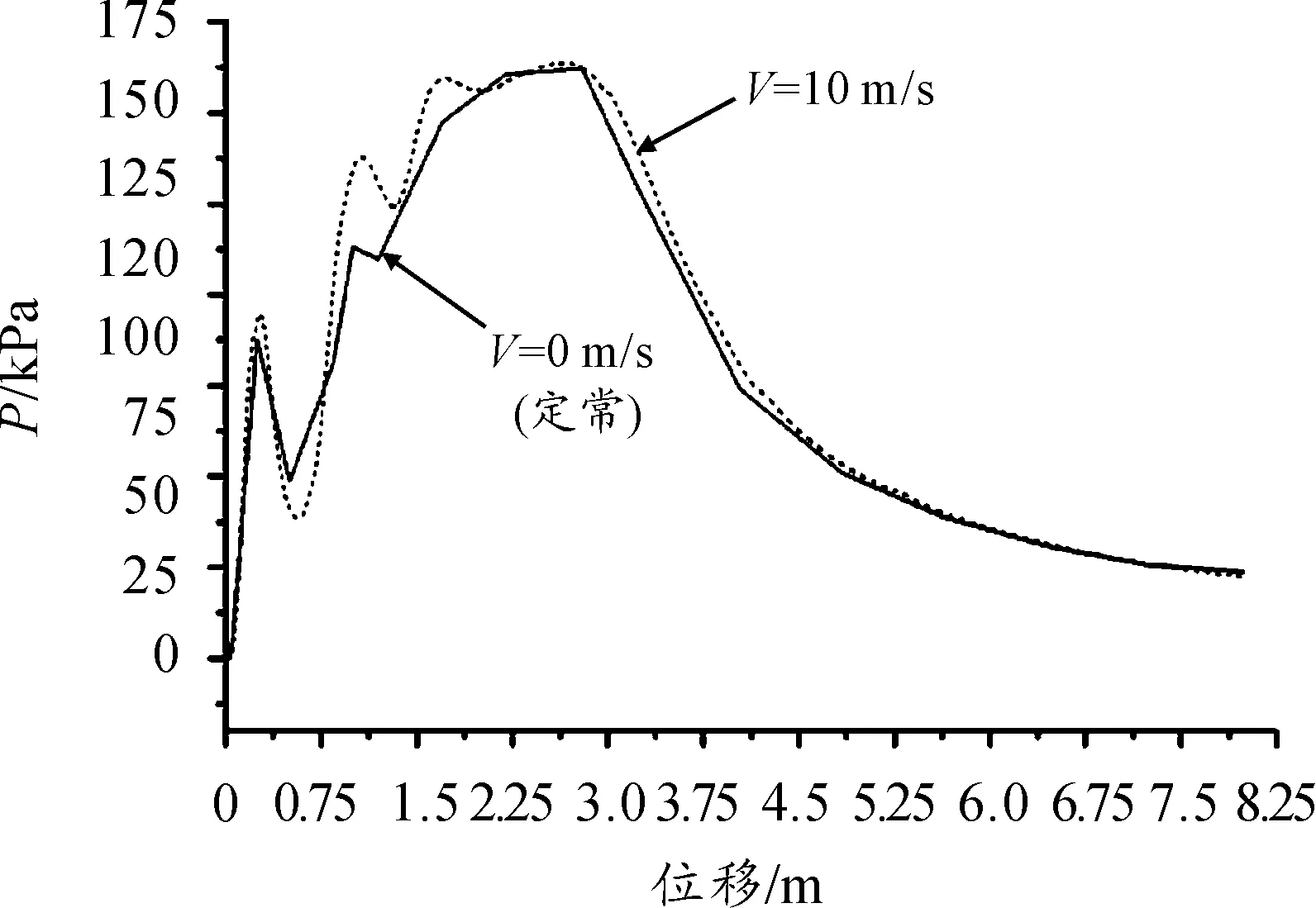
图9　调整特征位置以后最大压强计算结果

从图9和图10可以看出，按照第4节的思路调整定常计算特征位置以后，两种计算方法得到的结果相符程度大大提高。

5结论

不同火箭速度条件下，结构所受冲击作用随火箭行程变化趋势基本一致；结构所受射流冲击作用载荷峰值与火箭飞行速度呈反比关系；按定常方法计算时，计算的特征位置需要有针对性的选取，否则计算结果与用动网格计算结果差异较大；结合自由射流计算结果，将定常计算时的特征位置选取为射流的整数倍波节长度，可以得到与动网格方法较为一致的结果。

参考文献：

[1]刘琦,傅德彬,姜毅.贮运发射箱内燃气射流的非定常冲击波流场数值模拟[J].弹箭与制导学报,2005,25(2):382-384.

[2]刘群,姜毅,郝继光,傅德彬.燃气射流对发射车轮胎作用仿真[J].弹箭与制导学报,2005,25(4):720-722.

[3]刘群,姜毅,郝继光.燃气射流对发射车天线影响分析[J].弹箭与制导学报,2007(3):187-189.

[4]刘少伟,关娇,王伟,冯刚.燃气射流对多联装导弹发射箱前盖影响[J].空军工程大学学报(自然科学版),2013(2):32-36.

[5]王伟,王学智,刘少伟.倾斜发射导弹燃气流场数值模拟[J].弹箭与制导学报,2013(4):127-130.

[6]李军,马大为,曹听荣,林永明.火箭发射系统设计[M].北京:国防工业出版社,2008:52-62.

[7]单时卓,张艳.舰载导弹垂直发射过程中甲板面燃气流场仿真分析[J].火力与指挥控制,2014(3):73-76+80.

[8]傅德彬,姜毅.用动网格方法模拟导弹发射过程中的燃气射流流场[J].宇航学报,2007(2):423-426.

(责任编辑周江川)

Research on Relationship Between Rockets Flight Velocity and Jet Impact Effect

YANG Ming1, XIE Yu-tong2, WANG Hui1, XIA Sheng-yu1, WANG Ming-zhu1

(1.Research Institute of Sichuan Aerospace System Engineering, Chengdu 610100, China；2.Sichuan Aerospace Measurement and Test Research Institute， Chengdu 610100, China)

Abstract:The relationship between rockets flight velocity and jet impact effect was researched by CFD simulation. Different rockets flight velocity was simulated by dynamic mesh technology. The calculation results of steady method and dynamic mesh method were compared to analyze the causes for the difference and the selection method of feature position was given. The calculation result show the change trend of impact effect is much the same in different rockets flight velocity conditions, but peak load is inversely proportional to flight velocity. Steady method can get the similarity results of dynamic mesh method, but incorrect selection will cause significant differences. If feature position is chosen by free jet calculation results, the results of two methods will became close.

Key words:rockets flight velocity；jet impact；dynamic mesh；steady calculation；feature position

文章编号：1006-0707(2016)03-0027-04

中图分类号：TJ214

文献标识码：A

doi:10.11809/scbgxb2016.03.007

作者简介：杨鸣(1985—)，男，博士研究生，工程师，主要从事装备理论与装备技术研究。

收稿日期：2015-11-10；修回日期：2015-11-20

本文引用格式：杨鸣，谢雨彤，王辉，等.火箭飞行速度与射流冲击作用关系研究[J].兵器装备工程学报，2016(3):27-30.

【装备理论与装备技术】