分数阶偏微分电报方程一种解法的数值验证

杨云冲，徐忠昌

(海军工程大学 理学院，武汉　430033)



分数阶偏微分电报方程一种解法的数值验证

杨云冲，徐忠昌

(海军工程大学 理学院，武汉430033)

摘要：对于二维分数阶偏微分波动方程，前人通过差分格式离散的方法求出了数值解；为了进一步提高数值解的精度，减小误差，采用了另一种差分格式；传统的离散方式在所选择的离散点处直接按分数阶导数的定义离散，现在采取的方法是在所给相邻两个离散点连线的中点进行离散；为了证明此种差分格式是否有效，选取了一个数值算例进行编程计算。最终证明中点离散算法的数值解具有较高精度。

关键词:分数阶电报方程；数值解； 差分格式； 精度

Citation format:YANG Yun-chong, XU Zhong-chang.Numerical Test for a Solution to Fractional Telegraph Equation[J].Journal of Ordnance Equipment Engineering,2016(3):155-157.

由于分数阶微积分算子是拟微分算子，具有非局部性，因此分数阶微积分算子成为研究非线性问题的一个强有力的工具。近几十年来，许多研究者发现，分数阶导数的模型比整数阶导数的模型更能准确地描述具有记忆和遗传性质的材料和传送过程，故分数阶计算具有广泛的应用背景[1-5]。将研究带阻尼项的时间空间分数阶电报方程的数值解法，将使我们进一步了解电报传输过程中电流在不同位置与时间的关系，加深对类似模型的理解。在前人的研究中主要是潘有思用传统的离散方法求解了不带阻尼项的时间-空间分数阶偏微分电报方程[6]，并且通过一个数值算例验证了数值解的有效性，但是仍然存在一定误差。围绕计算结果的精确度能否进一步提高问题，本文在其基础上加以改进，并应用在另外一类带阻尼项的时间空间-分数阶偏微分电报方程上。本文所讨论的带阻尼项的时间空间分数阶电报方程的形式如下：

1差分格式

前人已经计算出此类方程中点处离散的差分格式，具体的内容简述如下：

由陈景华的结论[7-8]可知时域上的分数阶导数中点离散可写成：

由空间上的离散位移公式[9-10]，对空间变量的分数阶导数可以离散成：

以端点处的导数替代中点的导数可得：

令：

全部代入上式并考虑初始和端点条件，整理之后则方程可写成如下形式：

其中：

Pz=Az-2Az-1-Az-2

2数值证明

2.1给定方程

假定求解的电报方程如下：

其中自由项的表达式为

已知方程的精确解析解为

u(x,t)=x(x-2)t2

2.2差分格式有效性的数值证明

首先在时间和空间上取相对应的步长h=0.02,τ=0.01进行离散，并且编程运算，计算出数值结果。并分别在t=0.3,x=1的情况下取对应坐标轴上等间距采样点的数据制成表格和图像，分别如表1和图1，表2和图2所示，与对应精确解做出比较，求出误差。之后给出数值解与理论解的三维分布，如图3所示，从而分析该差分格式的有效性。Matlab编程计算结果如下：

分析表格中的数据我们可以得到在t=0.3时，绝对误差的最大值为0.000 6，相对误差的最大值为1.084 1%，处于较小的范围以内，同时由函数图像可以看出数值解的分布趋势和解函数的趋势保持了很好的一致性。

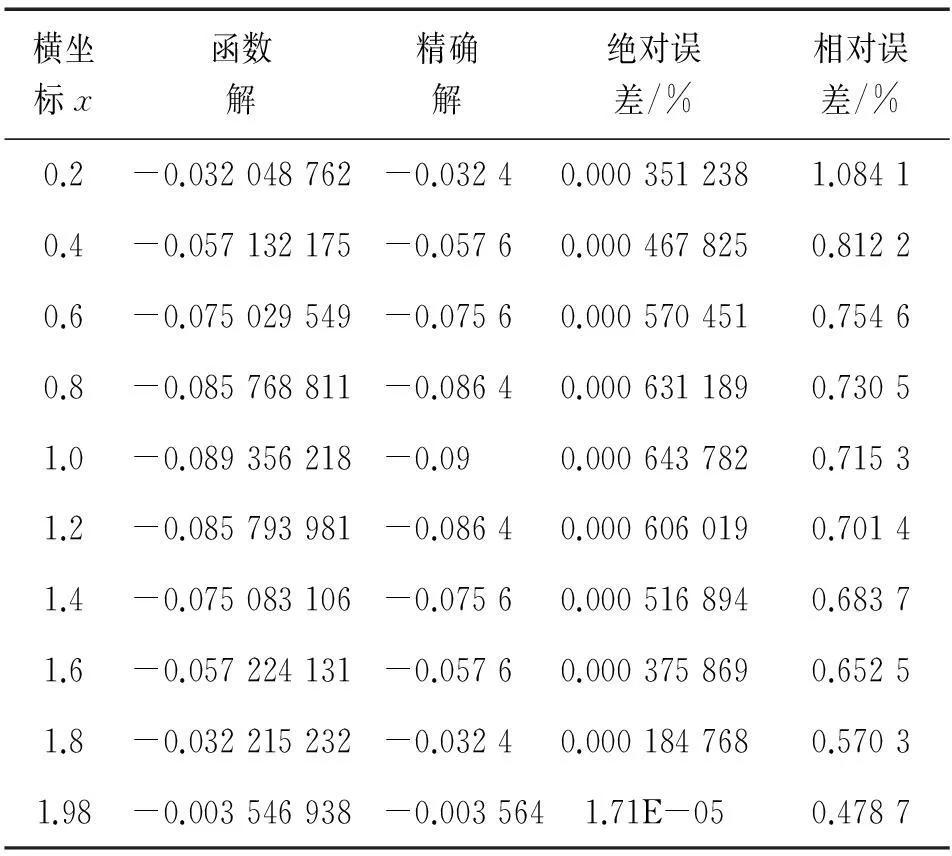
表1　t=0.3时数值解与精确解的比较

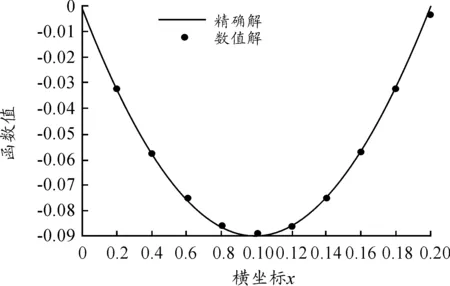
图1　t=0.3时的精确解与数值解

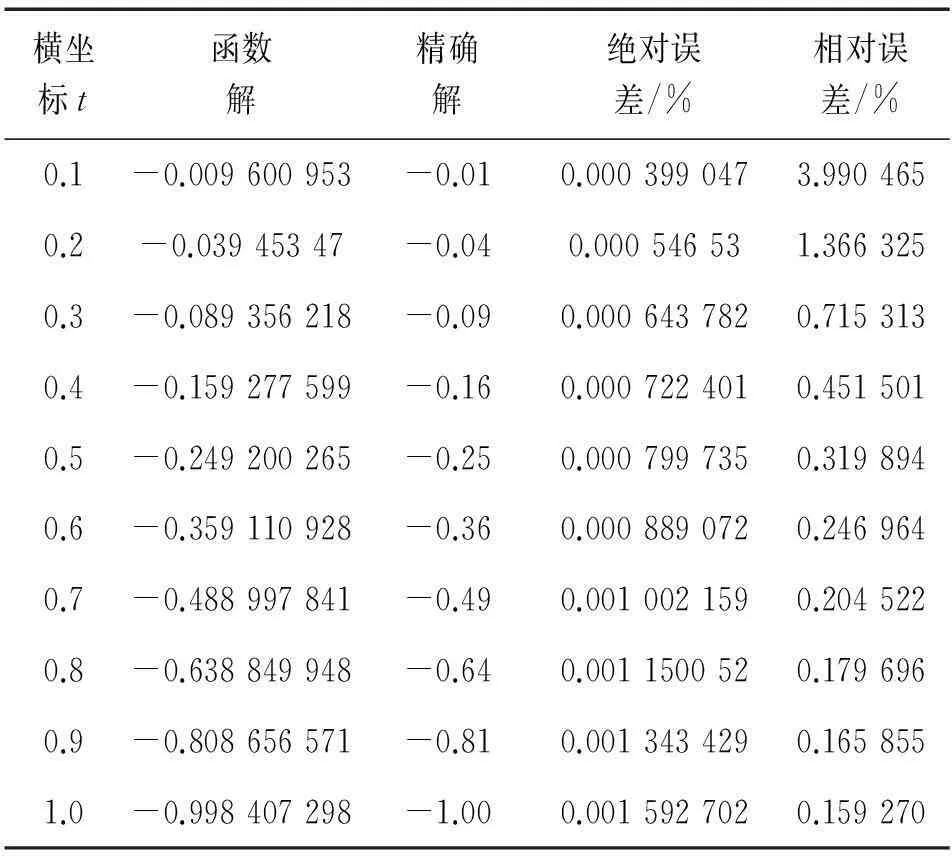
横坐标t函数解精确解绝对误差/%相对误差/%0.1-0.009600953-0.010.0003990473.9904650.2-0.03945347-0.040.000546531.3663250.3-0.089356218-0.090.0006437820.7153130.4-0.159277599-0.160.0007224010.4515010.5-0.249200265-0.250.0007997350.3198940.6-0.359110928-0.360.0008890720.2469640.7-0.488997841-0.490.0010021590.2045220.8-0.638849948-0.640.0011500520.1796960.9-0.808656571-0.810.0013434290.1658551.0-0.998407298-1.000.0015927020.159270

分析表格中的数据可以得到在x=1时，绝对误差的最大值为0.001 6，相对误差的最大值为3.990 465%，处于较小的范围以内，同时由函数图像可以看出数值解的分布趋势和解函数的趋势的一致性很好。

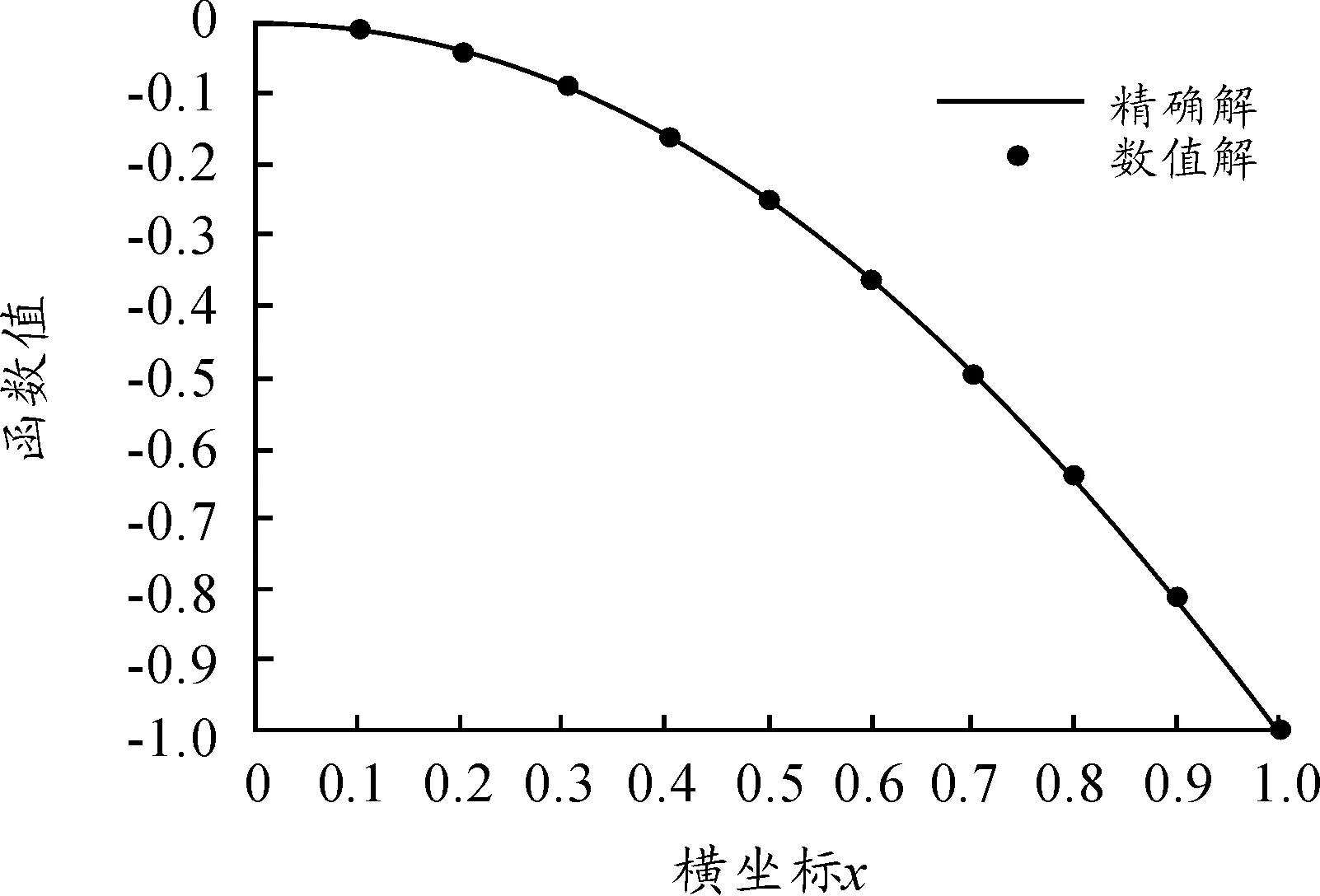
图2　x=1时的精确解与数值解

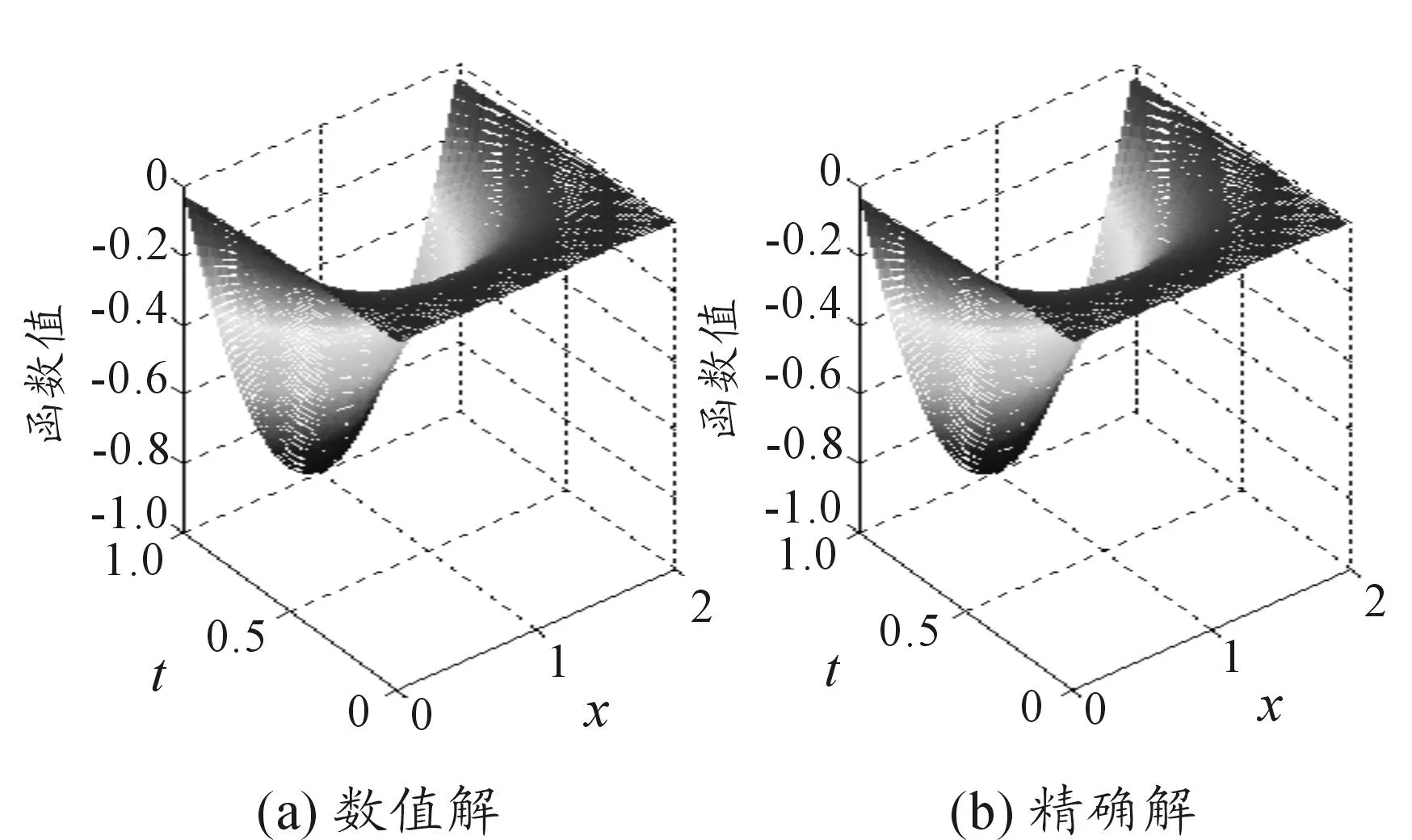
图3　数值解与精确解的三维比较

综合如上所有的计算数据表格和图像，可以看出该差分格式的在取100个离散点的情况下平均相对误差能控制在5‰左右，无论是在单个的二维平面或是在整体的三维立体图像中数值解与精确解的分布大致吻合，说明数值解精确和形象直观，最终证明此类差分格式在计算该型分数阶偏微分波动方程时非常有效，可以处理实际问题。

3结束语

本文通过Matlab编程计算，验证了中点离散法的数值解是有效的，能够很好地反映数值解精确和形象直观。但中点离散法的收敛速度和误差能否进一步缩小将是未来的研究方向。

参考文献：

[1]FRIENDRICH C.Relaxation Function of Rheological Constitutive Equations with Fractional Derivatives:Thermodynamical Constraints [J].Theological modeling:thermodynamic and statistical approaches.Casas-vasque J and Jou D,Berlin Springer,1991(9):320-330.

[2]GORENFLO R,MAINARDI F,MORETTI D,et al.Discrete Random Walk Models for Space-Time Fractional Diffusion[J].Chemical Physics,2002,284(7):521-541.

[3]METZLER R,KLAFTER J.The Random Walk’s Guide to Anomalous Diffusion:A Fractional Dynamics Approach[J].Phys.Rep.,2000,339:1-77.

[4]VALDES-PARADA F J,OCHOA-TAPIA J A,ALVAREZ-RAMIREZ J.Effective Medium Equation for Fractional Cattaneo’s Diffusion and Heterogeneous Reaction in Disordered Porous Media[J].Physica A,2006,369:318-328.

[5]HIFLER R.Applications of Fractional Calculus in Physics[M].Singapore:World Scientific,2000.

[6]潘有思.两类分数阶偏微分方程数值解法[D].哈尔滨：哈尔滨工业大学，2011:24.

[7]陈景华.时间和空间分数阶偏微分方程[D].厦门:厦门大学，计算数学2007:61-63.

[8]SUN Z Z,WU X.A Fully Discrete Difference Scheme for A Diffusion-Wave System[J].Applied Numerical Mathematics,2006,56(5):193-209.

[9]AGRAWAL O.Formulation of Euler-Lagrange Equations for Fractional Variational Problems[J].Journal of Mathematical Analysis and Applications,2002,272(1):368-379.

[10]MOMANI S.Non-perturbative analytical solutions of the space-and time-fractional Burgers equations.Chaos[J].Solutions and Fractional 2006(28):930-93.

(责任编辑唐定国)

Numerical Test for a Solution to Fractional Telegraph Equation

YANG Yun-chong, XU Zhong-chang

(College of Science, Naval University of Engineering, Wuhan 430033, China)

Abstract:For two-dimensional fractional telegraph equation, it’s numerical solution has already obtained based on difference approximation by predecessors.In order to promote accuracy, it obtained another form of difference approximation. Traditionally, people constructed a implicit difference approximation directly at the point discrete in the equation, while it operated at the position in the attachment middle of two close discrete points. Then in order to prove that the new method is practical, it was applied to a numerical example by programming and finally proved that the result of the new method is of high accuracy.

Key words:fractional telegraph equation; numerical solution; difference approximation; accuracy

文章编号：1006-0707(2016)03-0155-04

中图分类号：O241.82

文献标识码：A

doi:10.11809/scbgxb2016.03.037

作者简介：杨云冲(1991—)，男，硕士研究生，主要从事基础理论与应用研究。

收稿日期：2015-08-23；修回日期：2015-10-10

本文引用格式：杨云冲，徐忠昌.分数阶偏微分电报方程一种解法的数值验证[J].兵器装备工程学报，2016(3):155-157.

【基础理论与应用研究】