无人机远航飞行轨迹优化研究

高龙波，李本威，张　赟

(海军航空工程学院　a.研究生管理大队研究生五队； b.飞行器工程系,山东 烟台　264001)



无人机远航飞行轨迹优化研究

高龙波a，李本威b，张赟b

(海军航空工程学院a.研究生管理大队研究生五队； b.飞行器工程系,山东 烟台264001)

摘要:根据能量状态法对无人机给定燃油质量下的远航飞行性能进行了优化研究，对爬升和巡航段进行了远航轨迹优化分析，采用非线性规划理论对远航问题进行分析并利用SQP算法进行求解。通过分析某型无人机安全升限与质量的关系，提出了一种更适用于此型无人机的安全爬升优化方案。考虑此型无人机质量在巡航过程中变化较大，遂根据巡航质量分段进行速度优化，结果表明，巡航速度优化后的飞行距离大大增加。该研究方法简单，效果明显，实用性强。

关键词:能量状态法；轨迹优化；飞行性能；SQP算法

Citation format:GAO Long-bo, LI Ben-wei, ZHANG Yun.Flight Trajectory Optimization of UAV Long-Endurance[J].Journal of Ordnance Equipment Engineering,2016(3):94-97.

高空长航时无人机作战半径大，航时长，以其独特的优势越来越受到世界各国的重视。对此类无人机开展纵向剖面飞行轨迹优化研究，可以极大地提升飞行性能[1,5-7]。本文主要是对某型高空长航时无人机定燃油质量下的远航问题进行研究，一方面，在实际飞行中，大部分无人机的起降都采用标准程序，另一方面，该型无人机和发动机资料有限，尤其是与下降分析有关的发动机慢车性能数据缺失，所以依据能量状态法只对爬升和巡航段进行分析，并通过非线性规划的SQP算法进行求解。

1无人机航迹优化的动力学模型

无人机的轨迹优化主要是在纵向平面对其质心运动规律开展研究[2-4]，因此采用航迹轴系中的飞行器五阶运动模型

(1)

式中：T,D,L,α,φ,γ,VW,x,z分别为发动机推力、飞行阻力、飞机升力、飞行迎角、发动机安装角、航迹倾斜角、风速、地面坐标系中飞机质心的纵向和法向坐标。

2基于能量法的无人机轨迹优化计算

2.1无人机能量模型

能量状态法自20世纪50年代提出以来，不断应用于飞行器性能优化研究中，其理论基础和实践经验已经比较完善[1,5,9]。这里直接给出相关结论，不再推导。

对给定燃油质量下无人机的远航性能进行分析，重点考虑燃油成本指数，参看此类相关文献，性能指标定义为

(2)

定义单位质量下的总能量E为

E=H+V2/2g

(3)

该型无人机主要执行侦察任务，飞行中作以下假设：

1) 发动机安装角φ比较小，忽略其对推力的影响，令φ=0；

联立式(1)和式(3)，即得无人机运动的能量模型

(4)

2.2无人机航迹优化问题求解

对于航迹优化问题而言，本质上是一个多目标的优化问题，采用非线性规划方法可以很好地解决。非线性规划问题的一般形式为

(5)

根据最优控制理论中的变分法和极小值原理得到无人机在爬上和巡航阶段的目标优化函数λ、Iup，飞行过程中的速度、高度约束以及动力学限制条件即为hi(X)、gj(X)。

巡航阶段

(6)

爬升阶段

(7)

对此类含有非线性约束条件的目标优化问题，SQP算法是求解该问题的有效方法之一，其突出特点是算法简单、效率高、收敛效果好、边界区域的搜索能力强，利用数值仿真软件可以很方便地应用该算法求解优化问题。

另外，考虑发动机油门设置的灵活性理论上可以更加省油[6-7]，但在实际操作中，速度和高度选择对性能影响更重要，一般将油门设置为固定模式，即爬升采用最大油门模式，所以对速度、推力的寻优最终转换为对速度、高度的寻优。

2.2.1初始条件

依据该型无人机相关资料[6]，飞机升限20 km，合适巡航高度不低于15 km，最大飞行马赫数0.95，无人机起飞质量9 123.2 kg，燃油总质量5 170.1 kg，飞机余油和死油约占6%，所以航迹优化的初始条件定义为：初始爬升高度0.5 km，速度50 m/s，巡航高度15～20 km，巡航结束时飞机需保持10%余油，无风，不考虑无人机起飞过程的燃油消耗。

2.2.2计算步骤

无人机在巡航段，发动机工况为巡航态，性能指标中的P只与速度和高度有关，所以

(8)

给定巡航质量Wci，巡航性能指标随着高度、速度的变化关系如图1所示，可以看出低速下，巡航高度越低，λ越小；在较大飞行马赫数下，巡航高度越高，λ越小。

图1　λ与马赫数和高度关系

对于爬升段而言，Iup的计算需要先计算λ1，而λ1与巡航质量有关，因此需先计算巡航初始质量Wci。具体计算步骤依据文献[7-8]中所述，这里不赘述。

3无人机远航轨迹优化分析

3.1优化方案安全性分析

基于能量法的优化方案，其基本形式为：飞机从初始高度爬升到最优巡航高度，在此高度巡航至特定距离或者油耗后开始下降。依据2.2小节中的初始条件算得飞机最优巡航高度在升限处取得，最佳巡航马赫数0.655，爬升段燃油消耗为474.81 kg，因此目前的飞行方案为：无人机从0.5 km高度直接爬升到20 km，并以0.655马赫巡航飞行至10%余油。

对于此类高空长航时无人机，其实用升限定义为飞机以特定的质量和发动机工作状态作等速平飞时，还具有最大爬升率为0.5 m/s的飞行高度[2]。此高度是飞行品质不明显下降的前提下能飞的高度，此时飞机机动能力已经达到最低极限，一旦在飞行中遇到紧急情况，飞机的安全性难以保证。按照目前方案，一方面，无人机需长时间在升限处飞行，安全性不高；另一方面，能量状态法对高度的限制条件是T=D，由此求得的Hmax是理论静升限，而非实用升限。考虑到飞行安全性，有必要讨论该型无人机按目前的飞行方案能否直接爬升到20 km。

根据图2所示无人机爬升过程中质量变化情况，求得无人机在19 km附近爬升的参数变化情况。如图3所示，无人机在19 km附近爬升时最大爬升率小于0.5 m/s，这已经超过了实用升限对爬升率的要求，因此无人机直接爬升到20 km巡航飞行的方案安全性太低，需采用更适用于该型无人机的安全爬升方案，此时的高度约束条件应该是Vymax≥0.5 m/s。

图2　爬升过程无人机质量变化曲线

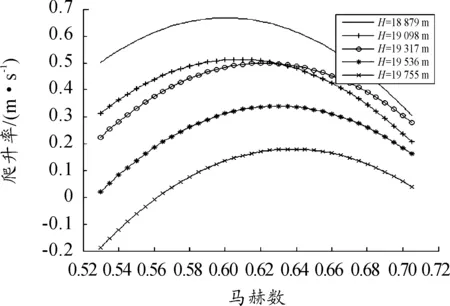
图3　无人机爬升率与马赫数关系(19 km附近)

3.2无人机安全飞行的优化方案

根据上述分析，无人机不能直接爬升至20 km，此时飞机质量偏大，因此飞机须先爬升至一个较低高度并在此高度巡航飞行，当质量下降到允许值，再爬升至20 km。

当飞行高度在17 km附近时，如图4所示，最大爬升率Vymax=6.7 km/h比较接近此类飞机对爬升率的要求[6]，因此选择17 km作为飞机首先巡航的高度，并在此高度巡航减重。

对于给定燃油质量下的远航问题，一方面巡航高度越大，性能指标越小，另一方面巡航初始质量越大，航程越远，而巡航质量又受到实用升限处爬升率的限制，因此需要求出无人机在20 km巡航飞行时所允许的最大质量W20max。在此方案下，按2.2小节中所述得17 km巡航开始质量为8 755.8 kg，巡航马赫数0.56。质量限制区间4 470.0 kg≤W20≤8 755.8 kg，速度限制区间0.5≤Mα≤0.7，目标函数Vymax≥0.5 m/s，求得W20 max为7 933.0 kg，进一步求得17 km爬升初始质量为8 014.16 kg。

图4　无人机爬升率与马赫数关系(17 km附近)

图5　速度与高度变化曲线

从图5可以看出，无人机在爬升过程中，需在较低高度先加速到120 m/s，在到达接近17 km的爬升高度时，速度已经达到了17 km的最大值164.8 m/s，大部分无人机在实际飞行过程中[9-11]也确实是这样飞行的，17～20 km爬升段也有类此情况发生。

3.3巡航段分段优化分析

20 km巡航段允许的燃油消耗量为3 463.00 kg，在整个巡航过程中保持巡航马赫数不变显然不是最优，无人机在20 km高度巡航时应该根据质量变化做变速飞行。这里说明为什么不对高度进行改变。

在巡航过程中，随着巡航质量的下降，飞机实用升限增加，根据巡航性能指标与高度、质量关系，理论上飞机在更高的高度巡航可以获得更优的远航性能，但是飞机在已达到设定升限的情况下，继续爬高，飞行器气动品质是否会发生较大改变，发动机高空稳定工作范围是否会急剧下降，飞行器在紧急情况下是否有足够的机动能力，都需要进一步分析，这对于工程应用来讲太过复杂。而且从图1中的进一步分析得知，随着高度的增加，同一马赫数下巡航性能指标差值Δλ越来越小，H≥17 km，Mα≥0.5以后，Δλ≤0.01，因此无人机在高于20 km高度进行巡航，效果不会很明显。另外，从图6可以看出，质量对Δλ影响较大。

因此从预期的优化效果出发，采用一维速度寻优方法，对20 km进行按质量分段优化，方法简单，实用性好。

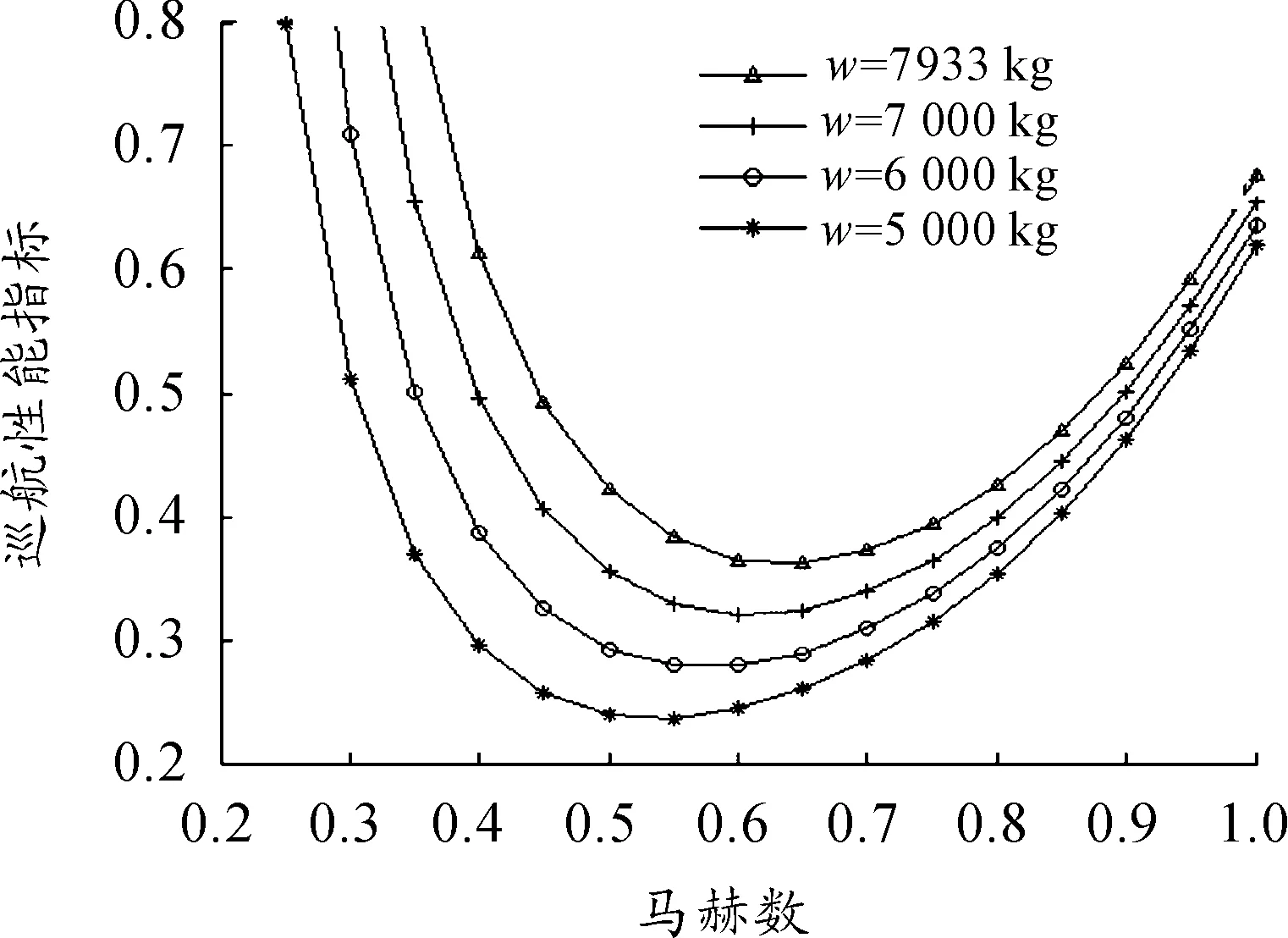
图6　巡航指标与质量和速度关系(H=20 km)

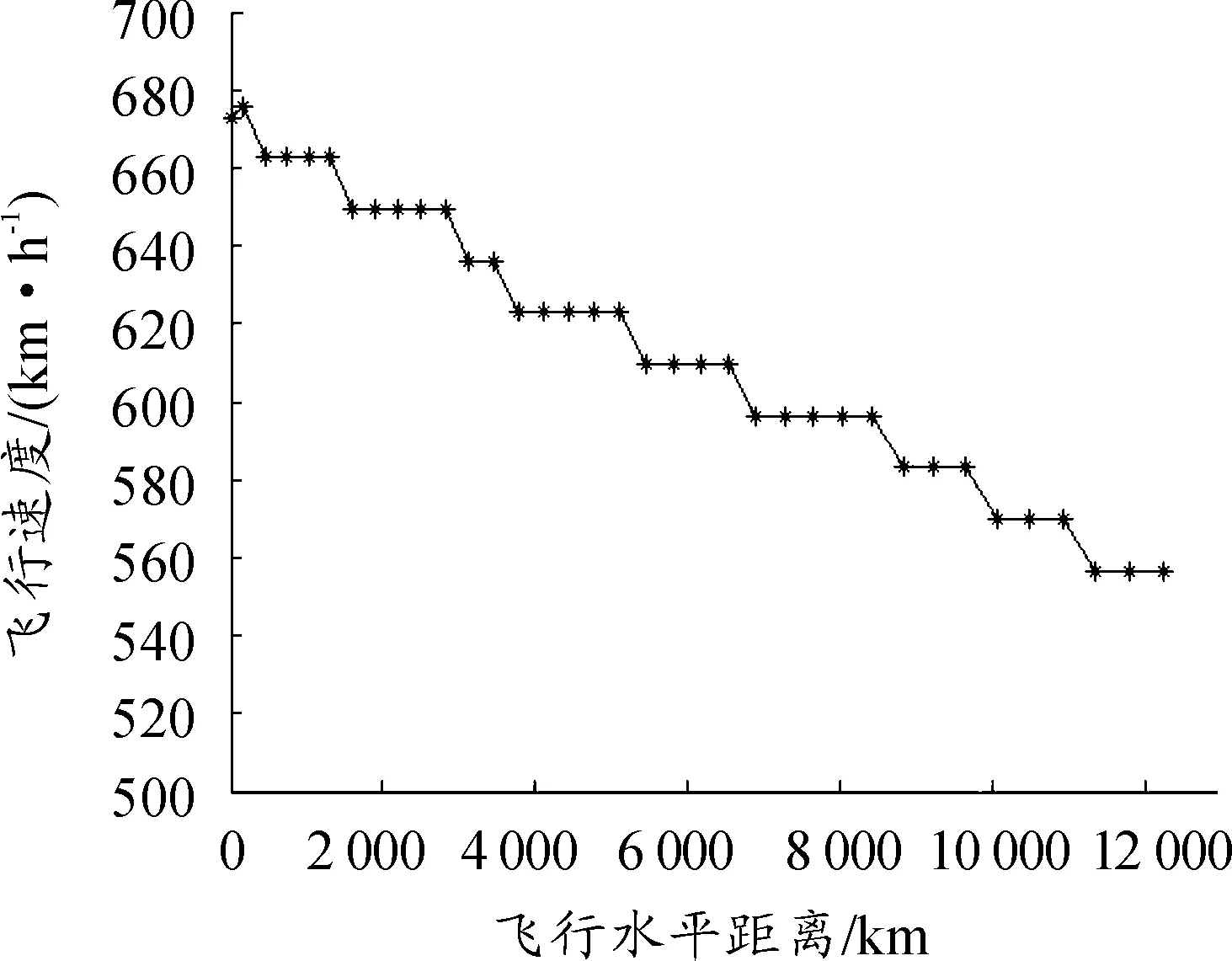
图7　分段巡航速度变化情况

根据巡航始末质量，将巡航段分为35段，并在每段进行速度寻优，从图6可以看出，随着飞机质量下降，H=20 km处无人机的最优飞行马赫数左移，图7表示了一维速度寻优后的变化情况，最优飞行速度不断减小，这种现象符合图6的规律。

飞行过程仿真数据见表1所示，仿真结果表明：质量分段后20 km巡航段飞行距离达到12 251.47 km，比定速巡航增加了2 666.64 km，远航性能获得很大的提升。

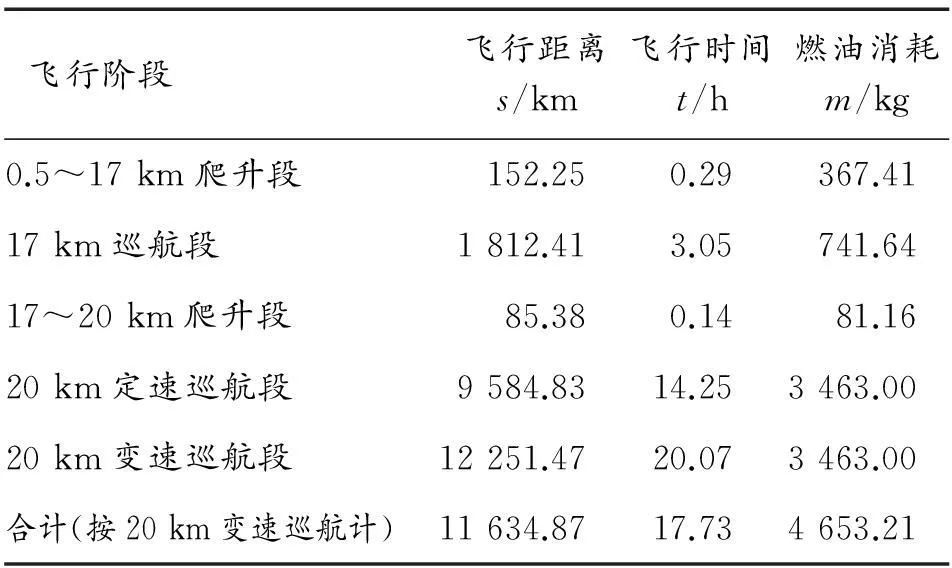
表1　飞行过程仿真结果

4结论

本研究对给定燃油质量下的某型无人机远航性能进行优化分析，重点讨论了质量与升限的限制关系，考虑飞行过程中的安全性提出将Vymax≥0.5 m/s作为约束条件。通过对该型无人机进行爬升-巡航轨迹优化，尤其是在巡航段按巡航质量分段速度寻优，无人机远航性能提升很大，有效地增强了无人机的侦察能力。

参考文献：

[1]沈勇璋.飞机纵向飞行轨迹的优化与实现[J].控制理论与应用,1992,9(4):380-386.

[2]方振平,陈万春,张曙光.航空飞行器飞行动力学[M].北京:北京航空航天大学出版社,2012:25-46.

[3]胡晓锋,贾秋玲,闫建国,等.无人机三维视景仿真系统实现[J].测控技术,2010,29(6):70-72.

[4]刘婕,易生勇.基于Matlab/Simulink的无人机飞行仿真研究[J].自动化信息,2012(8):50-51.

[5]陈晓,王新民,周健.基于序列二次规划法优化无人机飞行性能[J].计算机仿真,2012,29(12):99-101.

[6]邢博.高空长航时无人机综合优化设计[D].西安:西北工业大学,2007.

[7]徐启华,肖顺达,陈新海.基于总能量原理的飞行性能管理计算[J].西北工业大学学报,1994,12(1):25-30.

[8]《飞机设计手册》总编委会.飞机设计手册(第六册)[M].北京：航空工业出版社,2005.

[9]王伟,宁东方,张锦.基于能量状态法的飞机节油轨迹优化及其遗传算法实现[J].测控技术,2006,25(1):57-58.

[10]宋乐,赵淑利.以飞行成本最优为目的的大型飞机的性能优化[J].兵工自动化,2009,28(6):43-45.

[11]孙淑光,戴博,张鹏.飞机垂直剖面性能优化及仿真[J].控制工程,2011,18(4):600-604.

(责任编辑杨继森)

Flight Trajectory Optimization of UAV Long-Endurance

GAO Long-boa, LI Ben-weib, ZHANG Yunb

(a.The Fifth Unit of Graduate Students Brigade；b. College of Aircraft Engineering,Naval Aeronautical Engineering Institute, Yantai 264001, China)

Abstract:The method of energy-state was used for the long-endurance flight trajectory optimization study of a hele UAV. This thesis obtained the optimal climb-cruise trajectory of a hele UAV. The theory of nonlinear programming was used to slove the problem with SQP arithmetic. A better climb-cruise optimization plan was presented by analyzing the relationship between the security ceiling and the quality of a certain unmanned aerial vehicle. Considering the big changing of the UAV weight, the velocity needs to be optimized with different segments according to the quality of cruise. The simulation results show that the long-endurance flight performance improved a lot. The method of this thesis is simple, which also has obvious effect and strong practical applicability.

Key words:energy-state; trajectory optimization; flight performance; SQP arithmetic

文章编号：1006-0707(2016)03-0094-04

中图分类号：V249；TJ8

文献标识码：A

doi:10.11809/scbgxb2016.03.023

作者简介：高龙波(1990—)，男，硕士研究生，主要从事飞行器性能优化与综合控制研究；李本威(1964—)，男，教授，博士研究生导师，主要从事航空宇航推进系统理论与工程研究。

基金项目：山东省自然科学基金(ZR2013EEQ001)

收稿日期：2015-09-07；修回日期：2015-09-22

本文引用格式：高龙波,李本威,张赟.无人机远航飞行轨迹优化研究[J].兵器装备工程学报，2016(3):94-97.

【信息科学与控制工程】