圆锥曲线离心率解决漫谈
2016-05-05 12:02
高中数理化 2016年8期
圆锥曲线离心率解决漫谈
◇陕西呼延丽
分析2014、2015年全国30套高考理科数学试题,有关求离心率或给出离心率求其余量是高频考点,但离心率取值范围是这2年高考中的空白点.然而2013的15套理科高考数学试题中,有部分题目考到了离心率取值范围,这一现象给高三复习的老师带来一些思考,小题中可能会降低离心率取值范围的考查频率,或者将作为来年的考查对象.
1求离心率
1.1直接求出a、c




当曲线为椭圆时,2a=6k, 2c=3k,e=1/2. 当曲线为双曲线时,2a=2k, 2c=3k,e=3/2.
1.2构造a、c齐次式





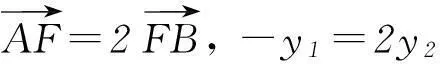


2离心率取值范围
求离心率取值范围要明确不等式思想,构建不等式是关键.
2.1利用圆锥曲线的范围构造不等式


(c-x)(-c-x)+y2=0,x2+y2=c2.
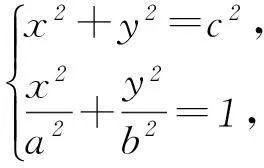




2.2利用二次方程判别式满足的条件构造不等式


2.3利用题设中其他变量的取值范围构造不等式


2.4以范围求范围(构造e=f(m))


从以上实例分析,求解离心率的问题一般采用构造关于a、b、c的齐次式或者e的等式,进而解方程;求取值范围的题一般需要根据题目中的条件和圆锥曲线本身的性质构建不等式解答.
(作者单位:陕西延安中学)
猜你喜欢
新世纪智能(教师)(2021年1期)2021-11-05
新世纪智能(教师)(2021年2期)2021-11-05
农机科技推广(2021年1期)2021-03-01
中等数学(2020年7期)2020-11-26
新世纪智能(教师)(2020年1期)2020-09-11
艺术品鉴(2020年6期)2020-08-11
新世纪智能(教师)(2019年1期)2019-09-11
中学生数理化·中考版(2018年9期)2018-11-09
中学生数理化·中考版(2017年9期)2017-12-20
新高考·高一数学(2016年3期)2016-05-19

