数形结合未必是一剂良药——记一道例题数学片断及反思



数形结合未必是一剂良药
——记一道例题数学片断及反思

◇江苏陈水青

数形结合思想是高中数学中一种重要数学思想,就是把数学中“数”和“形”结合起来解决数学问题的一种数学思想．数形结合具体地说就是将抽象数学语言与直观图形结合起来,使抽象思维与形象思维结合起来,通过“数”与“形”之间的对应和转换来解决数学问题．在应用其解题中,主要有3种类型:以“数”化“形”、以“形”变“数”和“数”“形”结合．

1解答

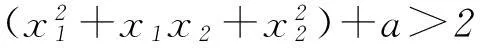
f(x1)-f(x2)>2(x1-x2),

f(x1)-2x1>f(x2)-2x2.

令g(x)=f(x)-2x,则g(x)在R上单调递增,所以g′(x)= 3x2+a-2≥0恒成立,所以a≥2.

解法3用到了构造函数的思想,把不等式作了一个等价变形,构造出g(x)=f(x)-2x,发现该函数单调递增,所以g′(x)≥0恒成立，利用导数解得a≥2．

2探究

为什么解法1是错误的?

图1

对于连续可导函数图象上任意一条割线,必定存在1条与之平行的切线吗(如图1)?

答案是肯定的,实际上就是拉格朗日中值定理(中学阶段不要求掌握)．

图2

反之,对于函数图象的任意一条切线,必定存在1条与之平行的割线吗?

答案是否定的．

例如,函数f(x)=x3+2x(如图2).其图象上有1条切线y=2x,但是图象上任取2点A(x1,y1)、B(x2,y2),过这2点的直线的斜率

不存在与切线y=2x平行的割线．

因此,割线的斜率k>2与导数f′(x)>2之间不是等价关系．对于函数图象的任意一条切线,不一定存在与之平行的割线,例如切线y=2x;平行的切线、割线不一定一一对应,不能用导数代替割线斜率．通过对比以上3种解法,解法3更具有一般性,对大部分函数适用．

3反思

2) 教学过程中要注重通性通法、一题多解、多题一解、举一反三、反三归一训练,努力培养学生的“6种能力、1个意识”,即运算求解能力、数据处理能力、空间想象能力、抽象概括能力、推理论证能力、实践能力和创新意识．现在高考比较重视的就是这种具有普遍意义的方法和相关的知识.教师在教学过程中千万不要为了展示自己而刻意追求一些解题的特殊技巧,在教学中不能把它当作重点,否则会误导学生.数学属于思考型的学科,在数学的学习和解题过程中理性思维起主导作用,教学过程中要更多地注重“一题多变”(类比、拓展、延伸)、“一题多用”(即用同一个问题做不同的事情)和“多题归一”(所谓“一”就是具有普遍意义和广泛迁移性的、“含金量”较高的那些策略性知识),更多地注重思考题目的“核心”是什么,从题目中“提炼”反映数学本质的东西.掌握好数学模式题的通用方法.

4举一反三

即

a>4x-x2=4-(x-2)2.

因为4-(x-2)2≤4,当且仅当x=2时,取“=”,所以a>4,所以a的取值范围是(4,+∞).

f(x1)-f(x2)>4(x1-x2),

f(x1)-4x1>f(x2)-4x2.

(作者单位：江苏省姜堰二中)