我国商业银行的系统性风险测度及影响因素研究——基于CCA-POT-Copula方法的分析

王　擎，白　雪，牛　锋

(1．西南财经大学 中国金融研究中心，四川 成都 611130；2.西南财经大学 金融学院，四川 成都 611130)



我国商业银行的系统性风险测度及影响因素研究
——基于CCA-POT-Copula方法的分析

王擎1，白雪1，牛锋2

(1．西南财经大学 中国金融研究中心，四川 成都 611130；2.西南财经大学 金融学院，四川 成都 611130)

摘要：本文基于CCA方法测度我国商业银行的个体风险，利用POT-Copula方法考察危机时期银行间违约相关性的变化，并对商业银行的系统性风险贡献及其影响因素进行实证分析。结果表明：在当前深化金融改革时期，我国商业银行的个体风险急剧攀升；与国有大型商业银行和城市商业银行相比，全国性股份制商业银行的系统性风险溢出效应总体较高；各商业银行的系统性风险贡献呈现明显的时变特征；杠杆率高、盈利能力强和业务复杂程度高的商业银行具有更高的系统性风险贡献。本研究为监管当局根据商业银行的系统性风险制定逆周期的宏观审慎监管政策提供了有益参考。

关键词：潜在损失；系统性风险；CCA-POT-Copula方法

一、引言

2008年发端于美国的国际金融危机暴露了金融监管体系对系统性风险的监管缺失,此后，系统重要性金融机构的识别以及金融体系宏观审慎监管成为国内外学术领域和监管部门关注的焦点。巴塞尔委员会2012年发布《国内系统重要性银行纲领》，指出一些金融机构即使全球系统重要性程度并不明显，仍可能对一国或地区的金融稳定产生重要影响。此后，各国掀起了研究国内系统重要性金融机构的浪潮。

长期以来，我国银行体系在分配资源、投资、风险管理等方面起着主导作用，但其内在风险也在不断积累。从空间维度看，我国金融机构尤其是商业银行的资产交叉性和同质性不断增强，增加了风险相互传染的可能性[1]；从时间维度来看，我国渐进式的金融改革导致银行风险过度集中与政府隐性担保加剧，增加了系统性风险聚集、金融体系崩溃的概率。在当前金融自由化和金融改革的大背景下，研究我国银行体系内部的经济相依关系、测度各银行在极端情形下的风险溢出效应以及潜在损失显得尤为重要。

国内外学者基于不同的视角提出多种方法测度金融机构的系统性风险。其中，网络模型法通过金融机构之间的实际业务往来数据估测其系统性风险大小，但信用数据的难以获得使该方法的应用受到限制；条件在险价值法(CoVaR)和边际期望损失法(MES)仅仅利用市场数据的单方面信息对金融机构的系统性风险进行度量，而我国股票市场的有效性不足降低了这类方法的可信度；未定权益分析法(CCA)同时运用金融机构的债务、市场收益等多方面信息测度系统性风险，却很少对金融机构之间的违约相关性加以考虑。

针对以上不足，本文首先，综合利用商业银行的财务报表数据和市场数据，采用未定权益分析法(CCA)量化商业银行的个体风险；其次，本文利用极值理论(EVT)和Copula函数，构建各商业银行与银行体系中潜在损失序列的尾部联合分布，合理刻画潜在损失序列的“厚尾”特征和非线性、非对称的尾部相依结构；在此基础上，我们采用滚动固定窗口的方法考察了商业银行系统性风险贡献的动态变化趋势。

本文结构安排如下：第二部分通过现有文献提出本文的研究思路；第三部分为研究设计；第四部分基于我国上市商业银行数据进行实证分析；第五部分是文章的结论及启示。

二、文献回顾

为了实施有效的宏观审慎监管，完善系统性风险监测预警和评估处置机制，各国学者从理论和实证方面对系统性风险做了大量研究。总体来看，分析金融机构间的相互关联以及对金融机构系统性风险进行测度的方法可大体分为两类，即结构化方法和简约化方法。

结构化方法主要通过各金融机构在风险头寸等方面的关联数据，研究系统性风险的传播路径及影响程度，其中以网络模型法最为典型。贾彦东，基于我国银行间支付结算数据构建金融网络模型，通过“直接贡献”和“间接参与”两种方式对商业银行的风险扩散机制进行分析，并对其系统重要性程度进行测评[2]；隋聪，等构建了完整的测度银行系统性风险和银行间违约传染的研究框架，并在此基础上研究了不同网络结构下的银行系统性风险[3]。网络模型法将系统性风险的传染与银行的实际交易相关联，使得传染路径有迹可寻，但该方法通常只能考察银行间实际业务往来的风险传染路径，而事实上银行间的风险传染存在广泛的间接渠道。

简约化方法不追究各金融机构之间的相互关联如何形成，而试图基于财务报表数据或股价等市场数据直接测度系统性金融风险。该研究方法可大致分为三种：综合指数法、市场法和未定权益分析法。

综合指数法在衡量系统性风险时，首先选取影响系统性风险的子指标构建衡量指标体系，然后利用统计方法将各指标进行综合，利用综合指数的大小反映系统性风险状况。Hakkio和Keeton基于美国数据构建了测度金融系统性风险的指标体系KCFSI，并验证了该指标体系可以有效印证已发生的金融危机[4]。刘春航等从宏观经济冲击、银行自身经营脆弱性以及传染等角度构建了我国银行业系统性风险的度量框架[5]。综合指数法虽然具有简单明了、可操作性强的优点，但指标选取的主观性和任意性较强，且无法度量金融机构的系统性风险贡献。

市场法通过股价等市场数据考察金融机构之间的风险相关性，进而基于不同视角对系统性风险进行度量[6]。其中，条件在险价值法(CoVaR)，是指单个金融机构处于困境时对其他金融机构或金融市场尾部风险的影响，现有研究大多采用△CoVaR测度金融机构的系统性风险贡献。高国华和潘英丽，基于GARCH模型计算商业银行的动态CoVaR，并认为该方法能够比传统的分位数回归更有效地度量银行的系统性风险贡献[7]。汪东华、陈守东，等将极值理论(EVT)、Copula理论引入到系统性金融风险的度量中[8-9]。系统性期望损失(SES)和边际期望损失(MES)方法考察了门限值以外的所有信息而非单一分位点的期望损失。范小云，等采用SES和MES的方法测度了在美国次贷危机时期，我国金融机构对金融系统的边际风险贡献程度[10]；方意，等利用SES和MES指标度量了我国金融机构的系统性风险，并对系统性风险的驱动因素进行了分析[11]。

未定权益分析法(CCA)可通过违约距离、违约概率、隐性担保等一系列风险测度指标衡量金融风险大小。范小云，等指出系统性违约距离与平均违约距离能够较好地反映我国银行系统性风险的动态变化[12]；而吴恒煜，等认为组合违约距离与平均违约距离之差更适合作为我国银行业系统性风险的测度指标[13]。部分学者通过隐性担保数据反映系统性风险大小，许友传，等结合我国特有的隐性保险和监管救助特点，运用CCA的分析框架估计了政府对我国上市银行的隐性救助概率和救助成本[14]；吴恒煜，等采用CCA方法测算我国商业银行的政府隐性担保，并指出在银行违约概率越大时政府对其隐性的担保则越高[13]。

在已有的研究成果中，CoVaR和MES方法仅仅运用了市场数据的单方面信息，而CCA方法在财务报表数据的基础上引入市场数据，能够考虑多维度的风险信息且不失前瞻性。然而，当前运用CCA方法的研究并未充分考虑危机时期银行间违约相关性的变化，且基于存款保险赔付的角度考察商业银行个体风险，同时对商业银行的系统性风险贡献进行动态度量的文章并不多见。

因此，本文首先综合运用CCA-POT-Copula方法，在测度商业银行潜在损失的基础上进一步考察商业银行的违约相关性，然后借鉴CoVaR方法的思想测度单个银行的系统性风险溢出效应并对其影响因素进行实证分析。理论层面上，本文基于存款保险赔付的角度测度银行业系统性风险，这在一定程度上丰富和拓展了系统性金融风险测度和传递理论的研究视阈；实践层面上，我们分别通过商业银行的潜在损失和△CoVaR*①测度其个体风险和系统性风险贡献的动态变化，并在此基础上探究商业银行系统性风险的驱动因素，能够为监管当局制定逆周期的宏观审慎监管政策提供有益参考。

三、研究设计

(一)基于CCA方法的潜在损失测度

1. 违约距离

未定权益分析法(CCA)利用Black-Scholes期权定价模型计算银行违约的可能性，一般假定银行的资产价值服从以下几何布朗运动：

dVt=μvVtdt+σvVtdWt

(1)

其中，μv和σv分别为银行资产的收益率及其波动率，Wt服从标准布朗运动。根据伊藤引理，银行的资产价值Vt服从以下对数正态分布：

(2)

这里，N(·)表示标准正态分布的累积分布函数，V0代表银行资产的初始价值。至负债到期日T时，若银行资产价值小于负债水平，则银行发生违约。因此，我们可以得到银行在t时刻预期的实际违约概率(Probability of Default，PD)为：

(3)

①本文借鉴传统△CoVaR思想，采用商业银行潜在损失数据而非市场收益率数据构造△CoVaR*。

式(3)中dt为违约距离。银行的股权价值Et可以看作以隐含资产价值Vt为标的、以负债的账面价值Bt为执行价格、以负债的到期期限T-t为持有期的欧式看涨期权，根据BS期权定价模型，其理论价值可以表示为：

(4)

根据伊藤引理，隐含资产波动率σv与股权市值波动率σE之间存在以下关系：

(5)

银行资产的期望收益率μv通常用无风险利率r代替，负债的到期期限T-t按照惯例取值为1年(许友传等[14]；吴恒煜等[13])，由以上公式可计算得到违约距离等风险测度指标。

2. 潜在损失

如果存款保险到期时银行的资产价值大于负债的账面价值，则保险公司支付的赔偿费用为零；反之，保险公司将支付银行负债与其资产价值的差额部分。根据Merton构建的存款保险定价模型，银行的风险债务Dt可看作以银行资产Vt为标的、以负债的账面价值Bt为执行价格、以负债的到期期限T-t为持有期的看跌期权[15]。根据看跌期权定价公式，存款保险机构到期的赔付为：

(6)

为了方便分析，本文将存款保险机构的到期赔付取为负值，代表商业银行的潜在损失(Potential Loss，PL)，即PLt=-Dt，整个银行体系的潜在损失(TPL)为各商业银行的潜在损失之和。银行潜在损失序列的测算步骤如图1所示。

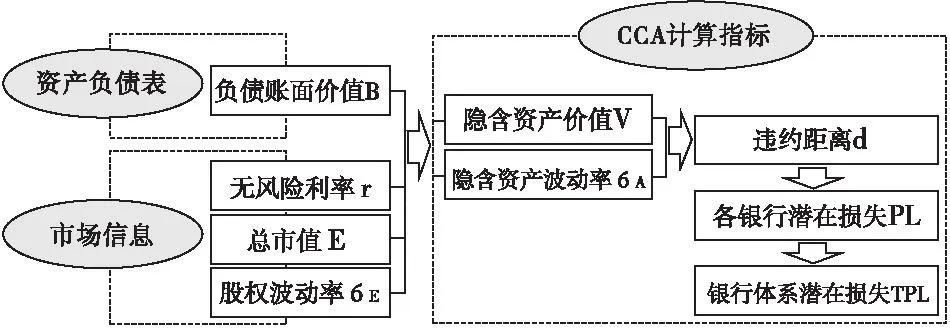
图1　CCA方法计算银行潜在损失步骤

(二)潜在损失的联合分布建模

1. 边缘分布的拟合

Pickands的研究表明，超过某一阈值的观测值渐近服从广义Pareto分布(GPD)[16]。则单个银行和整个银行体系潜在损失序列的边缘分布表示为：

2. 基于Copula的相依结构

Sklar提出的Copula理论通过将联合分布表示为各边缘分布的函数，极大拓展了多维联合分布的应用范围。其中，阿基米德Copula中的Gumbel Copula和Clayton Copula分别适合于右尾相关性较强和左尾相关性较强的相依结构建模，能够很好地捕捉随机变量之间非线性、非对称的相关关系，因此在金融风险管理领域得到广泛应用。Copula函数的选择一直是当前风险管理领域的难题，现有研究主要通过尾部相关系数、样本平均超越值、边际似然值等对Copula进行选择[18]。这里分别使用Gumbel Copula和Clayton Copula对潜在损失的左尾数据进行拟合，选择似然值较大的Copula构建潜在损失的联合分布。两类Copula对应的联合分布函数分别为：

(8)

(9)

式(8)和式(9)中G(x)、H(y)分别指单个银行和银行体系潜在损失对应的边缘分布。

(三)系统性风险贡献的度量

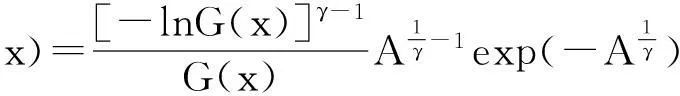
(10)

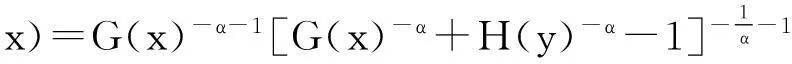
(11)

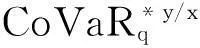
(四)系统性风险贡献的影响因素研究

我国的银行体系存在“太大而不能倒”和“太关联而不能倒”的现象。因此，从微观层面和宏观层面研究我国银行系统性风险贡献的影响因素，对维护国内金融稳定具有重要意义。本文以△CoVaR*作为被解释变量，根据已有研究(范小云等[12]；白雪梅等[20])，选取商业银行规模、杠杆率、不良贷款率、总资产收益率、业务复杂性以及与其他银行的关联程度等作为解释变量，以经济结构和经济增长等宏观经济因素作为控制变量，建立面板数据回归模型对银行系统性风险贡献的影响因素进行实证分析。具体回归模型如下：

(12)

其中，Size为银行资产规模的自然对数；Leverage表示银行的杠杆率；NPLR为银行的不良贷款率；ROA表示银行的总资产收益率；LR为银行的拆出资金与其自身资产规模的比例，代表银行与其他银行的关联程度；OR为银行其他业务收入占总营业收入的比例，表示银行自身经营的复杂程度；MGR为M2与GDP的比值，代表宏观经济结构；GDPG为GDP同比增长速度，表示宏观经济增长；εit为残差项。

四、实证结果分析

(一)样本与数据

本文选取的样本包括中国工商银行、中国银行、中国建设银行和交通银行4家国有大型商业银行，招商银行、平安银行、浦发银行、民生银行、华夏银行、兴业银行、中信银行7家全国性股份制商业银行，宁波银行、南京银行、北京银行3家城市商业银行。本文的研究区间选择为2007年第四季度到2014年底。

文中各上市商业银行财务数据和市场数据均来自wind资讯金融数据库和CSMAR研究数据库。无风险利率为中国人民银行公布的一年期定期存款基准利率与其实际执行天数的加权平均；为了得到商业银行每日的潜在损失，本文采用三次样条差值法将违约障碍的季度数据转变为日度数据；时变的股权波动率采用GARCH(1,1)建模获得。

(二)商业银行的潜在损失

1. 数据的统计特征

基于各商业银行的财务报表和市场数据，本文利用CCA方法得到各银行的潜在损失，表1报告了我国商业银行潜在损失的描述性统计结果。①由表1可以看出，各商业银行和银行体系的偏度系数均小于0，表明潜在损失序列具有明显的左偏特征，峰度系数均大于正态分布对应的3，呈现“尖峰厚尾”的特征；JB检验的p值均为0，则在5%的显著性水平下均拒绝原假设，表明各商业银行及银行体系潜在损失序列均显著异于正态分布。

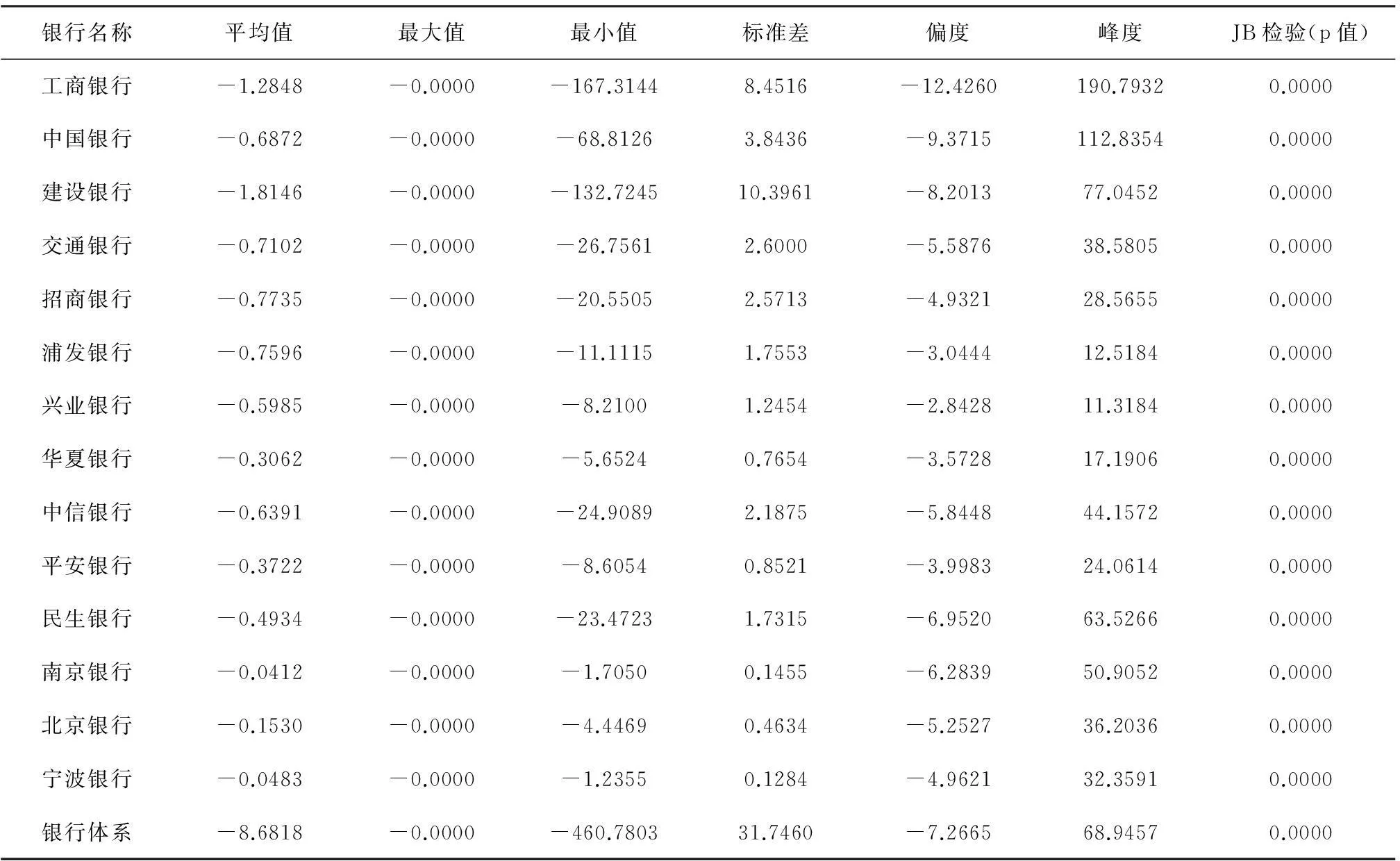
表1　潜在损失的统计描述

2. 潜在损失数据趋势分析

图2报告了研究区间内各商业银行潜在损失的变化趋势。为方便比较，我们将研究样本分为国有大型商业银行(图2-a)、全国性股份制商业银行(图2-c、2-d)和城市商业银行(图2-b)。从图2可以发现，总体来看，国有大型商业银行的潜在损失最高，全国性股份制商业银行次之，城市商业银行的个体潜在损失相对较小。

①潜在损失的单位为十亿元人民币，下同。

图2　各商业银行的潜在损失

注：为了方便分析，图中报告的是潜在损失的绝对值，数值越大表明商业银行的个体风险越大。

此外，我国银行体系的潜在损失具有明显的波动性。2007-2008年期间，受金融危机冲击，我国商业银行的整体风险较为突出；2010年欧债危机时期，由于国有大型商业银行国际业务占比相对较高，个体潜在损失明显上升，而全国性股份制商业银行和城市商业银行所受影响相对较小；2013年银行“钱荒”时期，全国性股份制商业银行和城市商业银行的风险明显增加，而国有大型商业银行风险无明显变化；2014年以来，随着我国利率市场化的推进以及人民币国际化等金融改革进程的加快，我国商业银行蕴藏的风险也在急剧攀升。

(三)边缘分布和Copula函数的参数估计

本文以两年作为时间窗口，通过滚动更新数据对商业银行以及银行体系的联合分布进行建模。表2报告了2013-2014年期间的参数估计结果，其中大多数银行的形状参数k大于零，表明潜在损失呈现出“厚尾、拖尾”的特征；而浦发银行、兴业银行、中信银行和平安银行的形状参数k小于零，说明潜在损失在极端值处具有“截尾”特征[21]。由于各商业银行与银行体系潜在损失序列具有非线性和非对称性的相关关系，我们采用Copula函数对该相依结构进行拟合，并根据极大似然函数值确定合适的Copula类型，由表2中Copula函数的选择及参数估计结果可以看出，不同商业银行与银行体系的相依结构存在明显差异。

(四)商业银行的系统性风险贡献

该部分基于单个银行与银行体系潜在损失的相依结构对各银行的系统性风险贡献进行度量。由于不同时期宏观经济状况和各商业银行的经营状况会发生变化，我们采用滚动固定窗口的方法测度不同时间段内各商业银行的系统性风险溢出效应。图3以5%分位点下的△CoVaR*为例，报告了我国各商业银行系统性风险贡献的变化趋势。

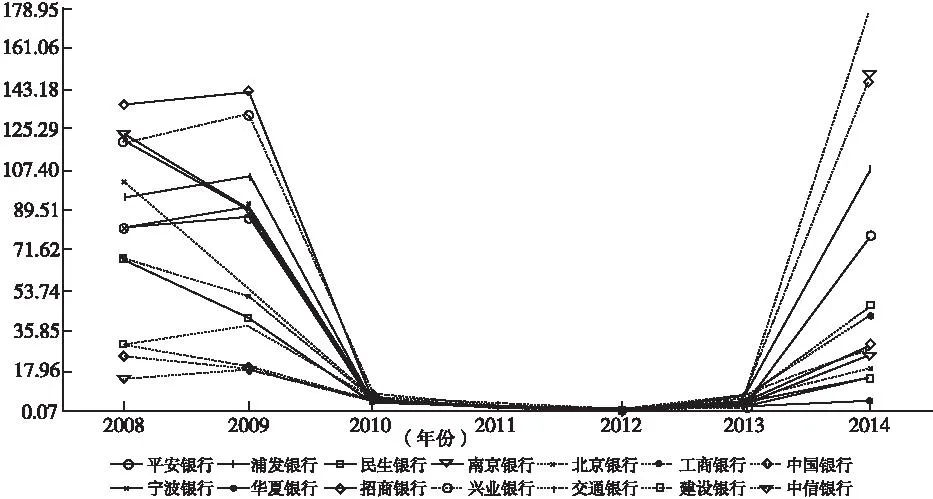
图3　我国上市商业银行的△CoVaR*_5%

注：(1)△CoVaR*的实际值为负，为方便分析图中均取其绝对值，数值越大表明系统性风险贡献越大。

(2)图中纵坐标单位为十亿元。

由图3可以看出，各商业银行的系统性风险贡献呈现明显的时变特征，其中在2008年金融危机时期，商业银行的系统性风险溢出效应整体较高，2010年之后有所回落并维持在较低水平，而2014年以来随着我国金融改革进程加速，各商业银行的系统性风险贡献迅速上升。整体来看，全国性股份制商业银行的系统性风险贡献较大，而国有大型商业银行虽然个体风险较大，但其对银行系统的风险溢出效应却相对较小。

表2　参数估计结果

表3选取2007-2008年金融危机、2009-2010年欧债危机以及2013-2014年我国深化金融改革时期三个区间，报告了我国商业银行系统性风险贡献的度量结果及其排序。

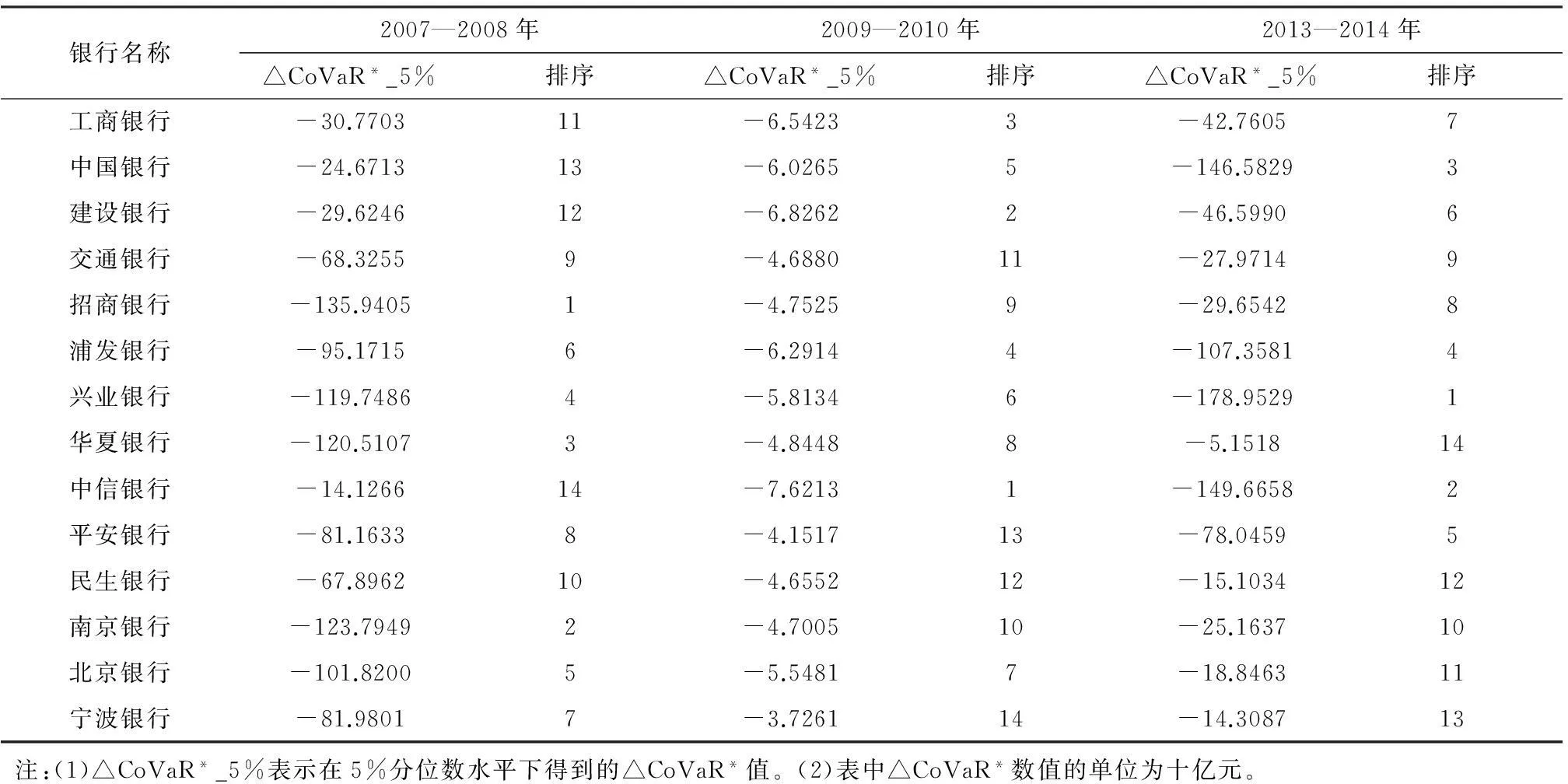
表3　我国商业银行的△CoVaR_5%

由表3可以看出，2007-2008年金融危机时期我国商业银行系统性风险整体较高，其中招商银行、南京银行和华夏银行等系统性风险贡献排在前列，而国有大型商业银行的系统性风险贡献相对较小。这一现象可能是由于中小型商业银行在金融危机前受利益驱使迅速增加杠杆，因而在遭到冲击时的风险溢出效应加大；而在此期间，国有大型商业银行杠杆率增加程度相对较小，系统性风险贡献也相应地较低。

2009-2010年欧债危机时期，各商业银行系统性风险贡献相对较小，中信银行和国有大型商业银行的系统性风险贡献排序靠前。这可能是由于欧债危机主要对我国银行业的国际业务产生较大冲击，而中信银行的国际业务一直领跑行业，国有大型商业银行的国际业务规模也相对较大，因此在这一阶段的系统性风险贡献相对较高。

2013-2014年深化金融改革时期，我国商业银行系统性风险的溢出效应整体较大。其中，兴业银行、中信银行等全国性股份制商业银行的系统性风险贡献较高，国有大型商业银行的风险贡献总体处于中间水平，城市商业银行风险贡献相对较小。近年来，由于股份制商业银行“影子银行”业务发展迅速，并且当前面临的市场定位、风险管理等问题较为突出，在深化金融改革过程中系统性风险增加迅速。而城市商业银行主要为地方经济以及地方居民提供金融服务，客户关系网络稳定，因此该时期系统性风险贡献相对较小。

(五)系统性风险贡献的影响因素

本文采用14家上市商业银行2007-2014年的年度财务数据对银行系统性风险贡献的影响因素进行实证分析，由于各时点的△CoVaR*值由历史两年数据计算得到，因此各解释变量取对应时间区间内的平均值。回归结果如表4所示。

表4中，10%分位点下的△CoVaR*对应的回归结果显示，Size的系数显著为正，表明银行自身的资产规模与其系统性风险贡献呈负相关关系，由于规模越大的商业银行经营的稳定性越好，在一定程度上其对银行业的系统性风险贡献就越小，这一结论与白雪梅和石大龙[20]的研究结果一致；Leverage系数显著为负，表明在发生危机时杠杆率越高的银行风险传染和风险溢出效应越大；ROA的系数显著为负，由于收益较高的银行往往从事具有更高风险的业务，因此在极端情形下的系统性风险贡献越高；OR的系数显著为负，说明银行的经营复杂程度越高，其经营风险越难掌控，相应的风险贡献就会越大。当以5%分位点下的△CoVaR*为被解释变量时，所得结论并无实质性差异。

表4　银行系统性风险贡献影响因素的实证结果

除了银行自身特征之外，宏观经济状况也对商业银行的系统性风险溢出效应具有显著影响。表4的实证结果表明，M2/GDP的值越大，即宏观经济杠杆率越高，商业银行的系统性风险溢出效应越大；此外，以GDP增速表示的实体经济波动同样会促进银行业系统性风险的扩散。

五、结论与启示

本文基于CCA方法测度了我国商业银行的个体风险，采用POT-Copula方法构建各商业银行与银行体系潜在损失的联合分布；在此基础上，我们对商业银行的系统性风险贡献及其影响因素进行实证分析。研究结果表明：(1)2007-2008年金融危机、2010年欧债危机、2013年银行“钱荒”以及2014年以来深化金融改革时期，我国商业银行的个体风险较大，潜在损失较高。(2)总体来看，尽管国有大型商业银行个体潜在损失较高，但其系统性风险溢出效应却相对靠后，而全国性股份制商业银行具有较高的系统性风险贡献。(3)各商业银行的系统性风险贡献呈现明显的时变特征，金融危机时期和当前深化金融改革阶段全国性股份制商业银行的系统性风险贡献较大，而国有大型商业银行在欧债危机时期系统性风险贡献排序明显上升。(4)杠杆率、总资产收益率和业务复杂程度越高的商业银行系统性风险贡献越大，宏观经济的杠杆率和波动性提高也会促进银行体系系统性风险的扩散。

本文结论对当前我国金融监管具有以下启示：第一，由于规模和业务特征存在明显差异，各商业银行在宏观经济冲击下的个体风险表现不同。因此，在深化金融改革时期政府部门应当针对不同类型的商业银行制定差异化的监管政策。第二，部分个体风险低的商业银行可能具有较高的系统性风险贡献，监管部门应当同时重视个体潜在损失和极端情形下的系统性风险溢出效应，将微观审慎和宏观审慎监管相结合。第三，各商业银行在不同研究区间内的系统性风险贡献存在差异，监管当局应当根据宏观经济环境变化对监管政策进行及时调整，提高金融监管的有效性。第四，一些规模相对较小、但杠杆率较高和业务较为复杂的商业银行具有较高的系统性风险贡献，政府部门应当结合银行规模、经营特点以及宏观经济状况等多重因素，完善相应的信息披露和资本附加制度。

参考文献：

[1] 刘春航,苗雨峰,朱元倩. 银行业同质性的度量及其对金融稳定的影响[J].金融监管研究,2012(2):18-31.

[2] 贾彦东. 金融机构的系统重要性分析——金融网络中的系统风险衡量与成本分担[J].金融研究,2011(10):17-33.

[3] 隋聪,迟国泰,王宗尧. 网络结构与银行系统性风险[J].管理科学学报,2014(4):57-70.

[4] Hakkio C S, Keeton W R. Financial stress: what is it, how can it be measured, and why does it matter? [J]. Federal Reserve Bank of Kansas Economic Review, 2009:5-50.

[5] 刘春航,朱元倩. 银行业系统性风险度量框架的研究[J].金融研究,2011(12):85-99.

[6] 徐超. 系统重要性金融机构识别方法综述[J].国际金融研究,2011(11):57-64.

[7] 高国华,潘英丽. 银行系统性风险度量——基于动态CoVaR方法的分析[J].上海交通大学学报,2011(12):1753-1759.

[8] 汪冬华,黄康,龚朴. 我国商业银行整体风险度量及其敏感性分析——基于我国商业银行财务数据和金融市场公开数据[J]. 系统工程理论与实践,2013(2):284-295.

[9] 陈守东,王妍. 我国金融机构的系统性金融风险评估——基于极端分位数回归技术的风险度量[J].中国管理科学,2014(7):10-17.

[10] 范小云,王道平,方意. 我国金融机构的系统性风险贡献测度与监管——基于边际风险贡献与杠杆率的研究[J]. 南开经济研究,2011(4):3-20.

[11] 方意,赵胜民,王道平. 我国金融机构系统性风险测度——基于DCC-GARCH模型的研究[J].金融监管研究,2012(11):26-42.

[12] 范小云,方意,王道平. 我国银行系统性风险的动态特征及系统重要性银行甄别：基于CCA与DAG相结合的分析[J].金融研究,2013(11):82-95.

[13] 吴恒煜,胡锡亮,吕江林. 我国银行业系统性风险研究：基于拓展的未定权益分析法[J].国际金融研究,2013(7):85-96.

[14] 许友传,刘庆富,陈可桢. 中国政府对上市银行的隐性救助概率和救助成本[J].金融研究,2012(10):60-74.

[15] Merton R. An analytic derivation of the cost of loan guarantees and deposit insurance: an application of modern option pricing theory [J]. Journal of Banking and Finance, 1977, 1(1):3-11.

[16] Pickands J. Statistical inference using extreme order statistics [J]. The Annals of Statistics, 1975, 3(1):119-131.

[17] Dumouchel W H. Estimating the stable index α in order to measure tail thickness: a critique [J]. Annals of Statistics, 1983, 11(4):1019-1031.

[18] Rocco M. Extreme value theory in finance: a survey [J]. Journal of Economic Surveys, 2014, 28(1):82-108.

[19] Adrian T, Brunnermeier M K. CoVaR [R]. FRB of New York Staff Reports, 2008:1-51.

[20] 白雪梅,石大龙. 中国金融体系的系统性风险度量[J].国际金融研究,2014(6):75-85.

[21] 桂文林,韩兆洲,潘庆年. POT模型中GPD“厚尾”性及金融风险测度[J].数量经济技术经济研究,2010(1):107-118.

责任编辑、校对：郭燕庆

The Systemic Risk Measurement and Influencing Factors of Chinese Commercial Banks—An Analysis Based on CCA-POT-Copula Method

WANG Qing1, BAI Xue1, NIU Feng2

(1. Center for Chinese Financial Research, Southwest University of Finance and Economics, Chengdu 611130, China; 2. School of Finance, Southwest University of Finance and Economics, Chengdu 611130, China)

Abstract:This paper measures the individual risks of Chinese commercial banks based on CCA method, investigates the interbank default relativity change in crisis period and empirically analyzes the systematic risk contribution of commercial banks and its influencing factors. The results show that: the individual risks of Chinese commercial banks rise sharply when the financial reform is being deepened currently. In comparison with that of large stated owned commercial banks and urban commercial banks, the spillover effect of the individual risks of Chinese commercial banks is generally relatively high. The systematic risk contribution of each commercial bank has clear time-change features. The commercial banks that have higher leverage, stronger profitability and more complex degree of businesses have higher systematic risk contribution. This study provides beneficial reference for the regulatory authority to make countercyclical macro-prudential regulation policy according to the systematic risks of commercial banks.

Key words:Potential Loss; Systematic Risk; CCA-POT-Copula Method

文献标识码：A

文章编号：1002-2848-2016(02)-0001-09

作者简介：王擎(1973-)，重庆市人，西南财经大学中国金融研究中心、金融安全协同创新中心教授，博士生导师，研究方向：宏观金融、公司金融、资本市场；白雪(1989-)，女，河南省周口市人，西南财经大学中国金融研究中心博士研究生，研究方向：宏观金融风险管理、资本市场；牛锋(1990-)，安徽省阜阳市人，西南财经大学金融学院博士研究生，研究方向：金融风险管理、实证资产定价。

基金项目：国家自然科学基金项目“银行资本约束下我国系统性金融风险传递研究”(71473200)；教育部人文社科重点研究基地重大项目“基于金融稳定的货币政策与宏观审慎监管协调配合研究”(15JJD790027)；2015年中央高校基本科研业务费专项资金项目“企业财务杠杆与银行业系统性风险”(JBK1507028)和“基于EVT-Copula的我国金融机构系统性风险研究”(JBK1507031)。

收稿日期：2015-11-17