货币政策对短期市场利率动态过程的影响——基于SHIBOR的实证研究
刘洪愧,王治国,邹恒甫
(1.中央财经大学 中国经济与管理研究院,北京 100081;2.北京大学 光华管理学院,北京 100871)
货币政策对短期市场利率动态过程的影响
——基于SHIBOR的实证研究
刘洪愧1,王治国2,邹恒甫1
(1.中央财经大学 中国经济与管理研究院,北京 100081;2.北京大学 光华管理学院,北京 100871)
摘要:本文基于上海银行间同业拆放利率(SHIBOR),构建引入货币政策变动的短期市场利率GARCH-JUMP模型,实证研究货币政策变动是否会促使SHIBOR发生剧烈的跳跃性现象。研究发现:(1)货币政策变动有助于解释短期市场利率的跳跃现象。其中,存款准备金率变动对SHIBOR的影响存在时滞,每周货币净投放变动则能够引起当期的利率跳跃;(2)引入每周货币净投放的模型在SHIBOR发生跳跃的时点上具有最大的条件方差,且跳跃部分的条件方差解释了该条件方差的绝大部分,而GARCH部分的条件方差则相对较小;(3)GARCH-JUMP模型中,事前与事后的期望跳跃次数在SHIBOR发生巨大跳跃时也会相应增加;(4)样本外的预测表现再次说明GARCH-JUMP模型在预测短期市场利率动态方面具有最高的拟合优度与最小的均方误。
关键词:货币政策;公开市场操作;短期市场利率;SHIBOR;GARCH-JUMP过程
一、引言
为了扭转2012年以来我国经济增速持续下滑的不利局面,一些学者提出政府应该尽快推动利率市场化改革,降低企业投融资成本,减轻实体经济运行的资金成本[1]。在市场化环境下,利率对经济活动的影响将进一步增强,并成为央行实施货币政策调控的主要工具之一[2]。央行通常选取最具代表性和影响力的短期市场利率作为基准,并采取盯住该利率的货币政策,即根据实体经济状况对其进行调整。例如美联储和欧洲中央银行分别盯住联邦基金利率和欧元银行间隔夜拆放利率。所以我国央行选择何种短期市场利率作为操作目标以及能否有效调致谢:感谢张定胜教授的宝贵建议,当然,文责自负。
控该利率将成为货币政策操作的关键。目前,我国货币市场中适合作为基准利率的有上海银行间同业拆放利率(SHIBOR)、银行间债券市场回购利率以及全国银行间同业拆借利率等。自2007年1月以来,SHIBOR运行稳定,以其作为定价参考的金融产品快速增加,基本能够及时反映我国货币市场的资金供求状况,很多研究也证明将其作为基准利率具有一定的可行性[3-4]。
然而,SHIBOR(包括其它短期市场利率)的时间序列存在经常性的向上跳跃、波动聚类及均值回归等现象。同时期,人民银行货币政策操作频繁,主要包括调节法定存款准备金率、公开市场操作、存贷款基准利率调整等。国外研究证明货币政策变动是造成短期市场利率波动的重要因素,主要通过两种机制实现:一是货币政策变动本身可以调节货币市场的资金供求,从而影响市场利率;二是货币政策变动能够传导央行对经济以及对货币市场风险的看法等以影响市场参与者的预期。那么中国的货币政策变动是否是以SHIBOR为代表的短期市场利率发生剧烈波动或者跳跃的重要因素?如果答案是肯定的,各种货币政策的影响又有何差异?对上述问题,国内的定量研究还较少。基于此,本文将在短期市场利率的动态模型中引入货币政策变量以深入研究这些问题。本文的研究有助于厘清各种货币政策影响短期市场利率的方式,强度和持续时间,对于利率市场化后中国的货币政策操作具有一定的指导意义,对货币市场参与者也有重要的参考价值。
二、文献回顾
在国外研究方面,本文总结了各种动态模型对短期市场利率的拟合效果;同时本文也将考察国内学者对以SHIBOR为代表的短期市场利率的研究。
早期的国外短期利率模型包括单因子模型[5-8]和多因子模型[9-11]。但是因子模型过度强调利率波动的水平效应而没能拟合条件方差的序列相关性,所以Brenner et al.[12]在扩散部分中引入GARCH效应,发现未预期到的信息冲击是造成利率波动的重要原因。Andersen 和 Lund[13]针对波动率构建随机波动模型并用有效矩方法估计了该模型。此外,部分学者还发现短期利率可能存在不止一种状态。所以Gary[14]以及Ang 和 Bakaert[15]用Hamilton[16]提出的马尔科夫机制转换模型研究美国的短期利率。虽然这些模型对正常状态下短期利率的拟合效果很好,但是它们都不能解释短期利率为什么会突然出现剧烈波动甚至跳跃。Das[17]提出未预期到的宏观冲击、突然的政策变化以及战争等信息冲击是短期利率发生跳跃的重要原因。而且Das[17]和Johannes[18]开发出GARCH-JUMP模型并引入这些经济变量以拟合短期利率动态过程,发现其能很好地拟合利率跳跃现象。
国内学者从两个方面对中国的短期市场利率进行了研究:第一,何种利率最适合作为市场基准利率;第二,市场利率动态过程的拟合。早期的研究如王建喜和王晓轩[19]认为由于我国的存贷款利率还没有放开,真正的市场利率是回购利率和国债利率。此后,梁琪等[20]对国内货币市场上各期限利率的研究发现SHIBOR作为市场基准利率的地位有待加强,其它几种市场利率仍发挥着重要作用。但方意和方明[3]对货币市场基准利率的研究显示SHIBOR作为市场基准利率的地位正在加强。总体来看,这些研究表明以SHIBOR作为短期市场利率的代表比较合适。在市场利率的动态过程研究方面,谢赤和吴雄伟[21]基于Vasicek模型和CIR模型对银行间同业拆放利率进行了实证研究,他们使用的是30天同业拆放利率的周加权平均值。洪永淼和林海[22]比较了单因子扩散模型、GARCH模型、马尔科夫机制转换模型以及GARCH-JUMP模型在7天国债回购利率市场上的表现,发现这些模型都不能准确描述7天回购利率。上述模型不能解释短期市场利率剧烈波动的重要原因在于它们没有考虑货币政策变动的影响。此后,张金清和周茂彬[23]在Vasicek模型中引入与宏观经济变量相关的跳跃成分,并用银行间债券市场7天回购利率的周数据进行实证分析。他们的研究显示加入宏观经济变量是必要的,现有的GARCH-JUMP模型不足以解释中国的短期利率。于建忠和刘湘成[4]从影响资金供求等货币市场因素方面建立一个SHIBOR定价的计量模型,但其并没有考虑SHIBOR的跳跃行为。
总体来看,已有文献还不能很好解释短期市场利率的剧烈波动,特别是跳跃现象。所以根据对SHIBOR动态过程的观察,并且借鉴国内外相关研究成果,本文拟用加入货币政策变动的GARCH-JUMP模型拟合中国的短期市场利率。具体的,在分别对照法定存款准备金率变动、每周货币净投放变动与SHIBOR的时间序列之后,本文发现这两者与SHIBOR的跳跃现象关系密切。所以我们将主要研究这两种货币政策操作对SHIBOR动态过程的影响,以及是否有助于对后者的预测,包括对其水平值和波动率的预测。
三、数据和计量模型
(一)数据
1.数据来源
本文所用的短期市场利率包括隔夜以及7天上海银行间同业拆放利率(以SHIBOR_O/N和SHIBOR_7D表示),来自于其官方网站www.shibor.org。中央银行公开市场操作形成的每周货币净投放(以NMT表示)来自于Wind资讯。法定存款准备金率(以R表示)和三个月定期存款利率(以RATE_3M表示)均来自于中国人民银行网站。以上数据的时间跨度为2007年1月4日到2014年5月30日。我们使用2007年1月4日到2013年1月18日的数据进行样本内估计,并使用2013年2月25日到2014年5月30的数据验证模型的预测表现。
2.数据处理和描述性统计
为了避免节假日造成的SHIBOR时间序列的非连续性,并且为了与中央银行的每周货币净投放数据频率一致,我们把SHIBOR日数据转化为周数据。图1(a)为SHIBOR_O/N和RATE_3M的时间序列图,图2为每周货币净投放的时间序列图。图1(a)表明SHIBOR_O/N和RATE_3M存在很强的正相关性。虽然SHIBOR_O/N短期内有可能偏离RATE_3M,但是从长期来看,SHIBOR_O/N会趋近RATE_3M,存在围绕后者的均值回归现象。另外,从图1(a)可以看到,RATE_3M只影响SHIBOR_O/N的水平,并不影响后者的波动率。此外,由于RATE_3M由中央银行外生给定,所以为了减少模型参数,我们以SHIBOR_O/N减去RATE_3M作为短期基准利率的代理变量,以SHIBOR_RATE表示,图1(b)描绘了其时间序列图。对比图1(a)和图1(b)可知相对于SHIBOR_O/N,SHIBOR_RATE更加平稳。
表1给出了SHIBOR_O/N、SHIBOR_RATE以及NMT的描述性统计量。从表1可知SHIBOR_O/N和RATE_3M具有较大的正偏度以及峰度,说明两者都不服从正态分布。同时根据Jarque-Bera(JB)统计量,我们也可以拒绝这两个序列服从正态分布的假设。因此,我们不能用一般的正态分布误差模型去拟合这两个序列,引入跳跃因子可能会更合理。每周货币净投放的偏度比较小,但是峰度比较大,说明每周货币净投放存在突然性的跳跃,这种突然性的政策变动可能是引发SHIBOR_O/N跳跃的原因之一。
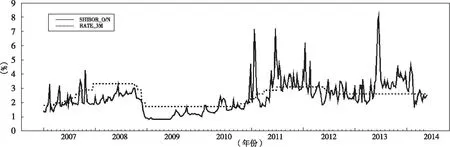
图1(a) 隔夜上海银行间同业拆放利率与三个月定期存款利率
注:图中实线表示隔夜SHIBOR,虚线表示三个月定期存款利率。

图1(b) 隔夜上海银行间同业拆放利率与三个月定期存款利率之差

图2 每周货币净投放

统计量隔夜SHIBOR(%)每周货币净投放(亿元)隔夜SHIBOR与三个月定期存款利率之差(%)均值2.3993.77-0.08标准差1.101252.300.92偏度1.43-0.202.31峰度4.2111.298.90JB统计量417.592059.571620.97JB统计量是否显著显著显著显著
(二)计量模型
国内外大量研究都说明短期利率动态过程表现出正偏、过度尖峰以及厚尾现象(Das[17];洪永淼和林海[22];张金清和周茂彬[23]),我们对SHIBOR的观察也证实这一点。这说明其扰动项不服从正态分布,所以许多学者提出用因子模型、GARCH模型和马尔科夫机制变换模型来拟合扰动项的方差。但这些模型仍不足以解释过度尖峰现象的事实,因此Das[17]、Johannes[18]以及Chan和Maheu[24]提出用GARCH-JUMP模型来拟合短期利率。GARCH-JUMP模型在标准GARCH模型的基础上增加跳跃因子以对扰动项建模,能够更好地刻画短期利率的过度尖峰。进一步,洪永淼和林海[22]的研究显示短期市场利率的纯GARCH-JUMP模型仍有缺陷,且认为央行的货币政策变化可能会造成其跳跃,即可以在该模型的跳跃因子中引入代表货币政策变化的变量。根据以上分析,本文将在GARCH-JUMP模型中引入货币政策变动以研究短期利率动态。
1.GARCH—JUMP模型的设定
令截止到时间t的历史信息为It,包括SHIBOR的历史利率水平以及历史的货币政策操作。计量模型设定为:
(1)
其中SHIBOR_RATEt=SHIBOR_O/Nt-RATE_3Mt,zt服从独立同分布标准正态过程,ht为条件波动率,服从GARCH(1,1)过程:
(2)
其中ut=SHIBOR_RATEt-α0-α1SHIBOR_RATEt-1。在稳健性检验部分,我们将令ht服从指数平滑移动平均过程(EWMA),即令(2)式中的β0=0, β1+β2=1。

λt=λ0+γ1|Ct|+γ2ηt-1
(3)
其中Ct代表货币政策变动,包括存款准备金率变动或者每周货币净投放变动,下文将分别给出它们的测度。ηt-1为基于t-1期信息求出的跳跃次数与基于t-2期信息求出的跳跃次数之差。根据泊松过程的性质可得:
λt=E(Nt|It-1)
(4)
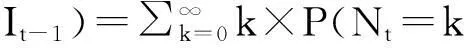
(5)

(6)
令f(SHIBOR_RATEt|Nt=k,It-1)表示给定t-1期信息以及t期跳跃次数时SHIBOR_RATEt实现值的概率,则由贝叶斯公式可得已知t期信息时跳跃次数为k的概率:
P(Nt=k|It)=f(SHIBOR_RATEt|Nt=k,It-1)P(Nt=k|It-1)/P(SHIBOR_RATEt|It-1)
(7)
由全概率公式可得:
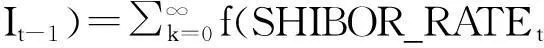
|Nt=k,It-1)P(Nt=k|It-1)
(8)
结合(1)式可得:


(9)
对于单次跳跃大小Jt,我们假设:
θt=ω0+ω1Ct
(10a)
(10b)
这种设定的优点在于Jt将随利率的条件波动率而变化,能够更好的捕捉跳跃动态。接下来我们将给出SHIBOR_RATEt的条件均值与条件方差。
E(SHIBOR_RATEt|It-1)=α0+α1SHIBOR_RATEt-1+λtθt
(11)

(12)
根据以上公式可构造关于{SHIBOR_RATEt}的最大似然函数,并利用最大似然法估计模型的参数。
2.政策变动的测度
存款准备金率和公开市场操作(主要表现为每周货币净投放)是中国最常用的货币政策工具。自2007~2012年,存款准备金率调整达35次之多;从2004年以来,央行票据已经成为中国人民银行公开市场操作的主要工具,其每周将进行货币投放与回笼操作。此外,国内大量研究也显示这两种货币政策对我国短期市场利率具有显著的影响。彭兴韵和施华强[25]建立VAR模型说明这两者会通过改变货币市场资金供求而对短期利率产生影响。张雪莹[26]采用事件研究法考察存款准备金率调节对各类市场利率的影响。另外,每周货币净投放也会通过泰勒规则而影响短期利率[27]。所以本文将在GARCH-JUMP模型中引入这两种货币政策。
对于存款准备金率,其调整幅度仅限0.5%或1%,参照张雪莹(2012)[26]的虚拟变量方法,本文定义存款准备金率变动如(13)式。因为存款准备金率的下调(上调)意味货币供给的增加(减少),会使得利率向下(上)跳跃,所以RCt为负值(正值)。
(13)
令每周货币净投放为NMTt(净货币投放量),标准化的每周货币净投放变动的测度为SDNMTt,并令s为序列NMTt-NMTT-1的样本标准差,则:
(14)
3.五个估计模型

模型一:SHIBOR_RATEt=α0+α1SHIBOR_RATEt-1+
表示扰动项只服从GARCH(1,1)过程。
模型二:SHIBOR_RATEt=α0+α1SHIBOR_RATEt-1+
其中令Ct=0,表示没有引入货币政策变动的GARCH-JUMP模型。
模型三: SHIBOR_RATEt=α0+α1SHIBOR_RATEt-1+
其中令Ct=SDNMTt,表示引入每周货币净投放变动的GARCH-JUMP模型。
模型四: SHIBOR_RATEt=α0+α1SHIBOR_RATEt-1+
其中令Ct=RCt,表示引入当期存款准备金变动的GARCH-JUMP模型。
模型五: SHIBOR_RATEt=α0+α1SHIBOR_RATEt-1+
其中令Ct=RCt-1,表示引入前一期存款准备金变动的GARCH-JUMP模型。
四、估计结果分析
(一)基本估计结果
我们使用Winrats软件,运用最大似然方法估计了模型一到模型五的参数,结果见表2,其中α0和α1表示自相关参数,β0、β1和β2表示GARCH过程的参数,ω0和ω1代表单次跳跃大小的均值参数,ρ0和ρ1代表单次跳跃大小的方差参数,λ0、γ1和γ2代表跳跃强度参数。
模型一的估计结果显示,GARCH(1,1)过程的参数都很显著,说明短期市场利率的扰动项存在明显的条件异方差。但是常数项β0很小且在5%的显著性水平下不显著,同时我们也在模型一中限定β0=0,发现拟合结果比没有限定的情况更好,故在接下来的几个模型中我们限定β0=0。模型二到模型五的跳跃大小与跳跃强度的参数都很显著,同时,模型三到模型五的GARCH过程的参数都比模型一降低很多,这说明引入跳跃因子有助于解释短期利率的剧烈波动。为了更好地拟合跳跃强度与跳跃大小,我们在跳跃强度与跳跃大小的期望值中引入了货币政策变量。首先,模型三ω1的估计结果表明,每周货币净投放与跳跃大小存在正相关关系,且在1%的显著性水平下显著。同时,γ1的估计结果显示每周货币净投放的变动越大,则跳跃强度越大,且在5%的显著性水平下显著。从模型四和模型五中的ω1和γ1的估计结果可以看出,存款准备金率的变动在当期不会引起跳跃强度与跳跃大小的显著变动,也不会显著增加下一期的跳跃大小的期望。但是会增加下一期的跳跃强度,从而引起短期利率的跳跃现象。其次,从五个模型的对数似然值和Q(15)统计量可以看到,引入每周货币净投放的跳跃模型拟合效果更好;且在跳跃模型中引入上一期的存款准备金率变动比引入当期的存款准备金率变动更好。最后,不同的货币政策工具对短期市场利率的影响存在差异。法定存款准备金率的提高能够在一定程度上增加市场利率的跳跃强度,但是存在一定的时滞,而公开市场操作能够迅速影响短期市场利率。另外,我们发现,公开市场操作在提高短期市场利率单次跳跃大小上作用更强,但是在增加跳跃强度上的作用比法定准备金率要弱。

表2 GARCH-JUMP过程的估计结果
注:括号内的数字表示t统计量的值,t值>1.65(>1.96或>2.57)分别表示在10%(5%或1%)的显著性水平下显著。(下同)
(二)条件方差比较
货币政策不仅通过影响跳跃强度与跳跃大小而影响短期市场利率,而且能够通过改变条件方差(计算方法见(12)式)而造成短期市场利率的剧烈波动。在图3中,我们描绘了模型一、二与三的条件方差时间序列图,以便识别这些模型在条件方差上的差异。从图3中我们可以看出GARCH模型(模型一)的条件方差最小,模型二的条件方差次之,引入货币政策变动的模型三的条件方差最大。如果用前两个模型来拟合和预测短期市场利率,会使得短期利率的拟合值和预测值相对实际值来说过于平稳,不能充分的反映其跳跃现象。加入货币政策变动的跳跃模型由于考虑到了货币政策可能造成的短期利率的跳跃,能够更好的拟合条件方差,进而识别出可能的跳跃。
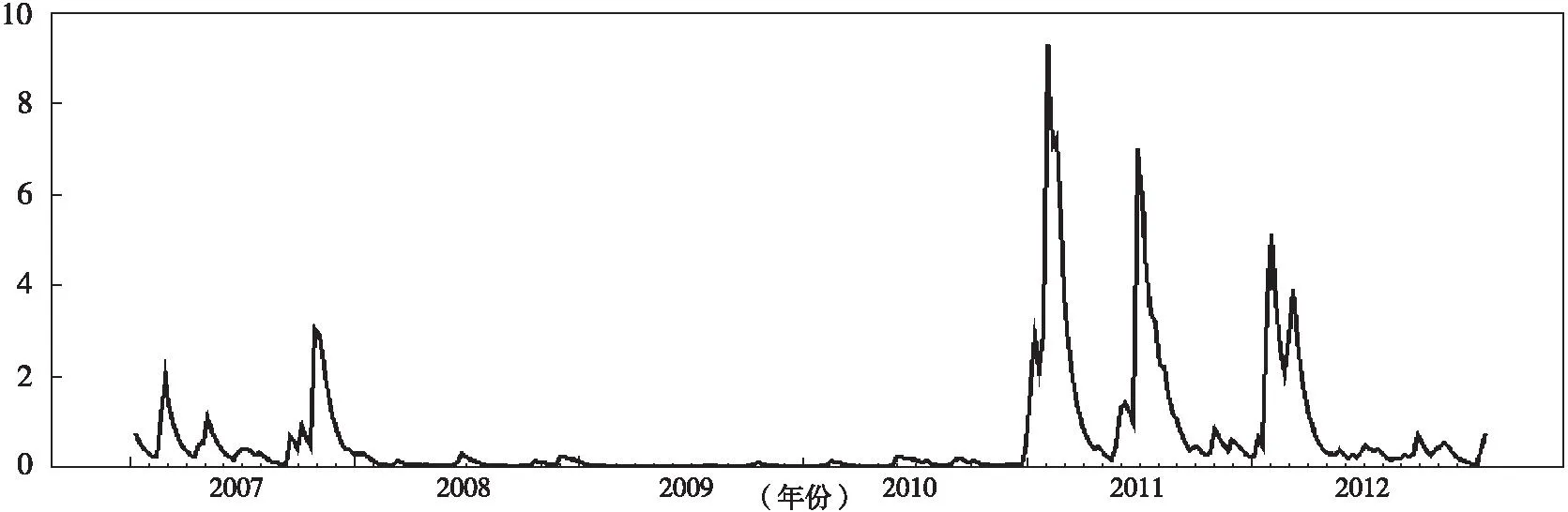
图3(a) 模型一的条件方差

图3(b) 模型二的条件方差图3

图3(c) 模型三的条件方差
(三)货币政策跳跃模型中条件方差的分解
进一步,条件方差可以分解为GARCH部分和跳跃部分。图4为图3(c)的分解,其中图4(a)和图4(b)分别为GARCH部分和跳跃部分的条件方差。可见,跳跃过程解释了条件方差的绝大部分,是造成短期市场利率波动的主要原因。为了说明这两者之间的关系,图5给出了跳跃方差与短期市场利率的时间序列图,从图5可知,跳跃方差非常大的同时,短期市场利率正好发生剧烈波动,两者存在显著的正相关关系,相关系数为0.23。这说明GARCH-JUMP模型对短期市场利率的拟合比较合理。
(四)事前与事后的期望跳跃次数
跳跃次数也是造成短期市场利率剧烈波动的原因,跳跃次数与单次跳跃大小之积为模型二到模型五中短期利率总的跳跃幅度。如果模型准确拟合了短期市场利率,那么当其发生巨大的向上跳跃时,事前与事后的期望跳跃次数也应更大。这意味着我们能对比它们与短期利率的时间序列图以验证GARCH-JUMP模型的拟合效果。图6和图7给出了模型三的事前与事后的期望跳跃次数。事前的期望跳跃次数(基于t-1期的信息计算)为λt。事后的期望跳跃次数(基于t期的信息计算)可由公式(4)、(5)和(6)得出。很明显,事前与事后的期望跳跃次数都和短期利率之间存在很强的正相关性,当后者发生跳跃时,前两者也往往处于峰值。这说明我们的模型较好地解释了短期利率的跳跃现象。

图4(a) 模型三GARCH部分的条件方差
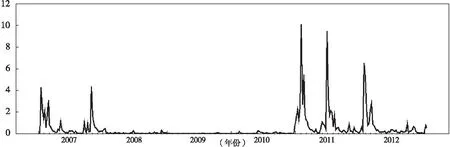
图4(b) 模型三跳跃部分的条件方差

图5 跳跃方差与短期市场利率
注:图中实线表示跳跃方差的大小,虚线表示短期市场利率(SHIBOR_RATE)。

图6 模型三事前的期望跳跃次数
注:图中实线表示事前的期望跳跃次数,虚线表示短期市场利率(SHIBOR_RATE)。

图7 模型三事后的期望跳跃次数
注:图中实线表示事后的期望跳跃次数,虚线表示短期市场利率(SHIBOR_RATE)。
(五)稳健性检验
为了检验GARCH-JUMP模型的可靠性,我们以7天的SHIBOR替代隔夜SHIBOR重新对模型参数进行估计,结果见表3。需要提及的是,我们在模型一中限制GARCH过程的常数项为0,且在模型二、三、四及五中以指数平滑移动平均过程(EWMA)取代了GARCH(1,1)过程①。比较表2和表3,我们看到大部分参数的估计结果基本不变。两类货币政策变动仍能够有助于解释7天SHIBOR的剧烈跳跃行为。其中当期的每周货币净投放对当期短期市场利率单次跳跃大小的影响还是很显著,而当期及前一期的准备金率变动分别通过改变跳跃强度和大小影响短期市场利率。此外,对数似然值也显示引入货币政策变动的GARCH-JUMP模型拟合效果更好②。

表3 7天SHIBOR替代隔夜SHIBOR的估计结果
①我们以指数平滑移动平均过程(EWMA)取代了GARCH(1,1)过程的原因在于,表3中模型一的估计结果显示β1和β2之和基本上等于1,而此种情况下的GARCH(1,1)过程等价于EWMA过程。
②限于篇幅,该部分没有给出条件方差及其分解,事前与事后的期望跳跃次数的相关图形,有兴趣的读者可以向作者索取。
五、模型预测表现
上文已经证明引入货币政策的GARCH-JUMP模型对短期市场利率有很好的样本内拟合表现,但还是有必要验证模型的样本外预测表现。我们从短期市场利率预测值对实际值的解释力,以及预测均方误两个方面比较了模型一、二和三以及AR(1)模型的样本外的预测表现。
(一)预测值对实际值的解释力
首先,我们用递归方法获得了隔夜SHIBOR_RATE从2013年2月25日到2014年5月30日的向前一期的预测值。我们用2007年1月5日到2013年1月18日的样本估计模型参数,然后用这些参数求得下一期的利率预测值,保持估计窗口不变,重复该过程,可以得到71个预测值。然后,以预测值为解释变量,真实值作为被解释变量进行线性回归,结果见表4,根据模型的R2,我们可知预测值在多大程度上解释了真实值。从表4中可以看到,引入货币政策变动的模型三的R2最大,模型二与模型一的R2次之,AR(1)模型的R2最小。所以,引入货币政策变动的GARCH-JUMP模型具有最好的预测效果。

表4 各模型的样本外预测表现
(二)预测均方误
此外,用真实短期市场利率值减去预测值可以得到预测误差序列,进而求得预测均方误(MPSE)。结果见表5。从表5可以看到,模型三的预测均方误最小,比模型二的MPSE小2个基点,比模型一的MPSE小4个基点,比AR(1)模型的MPSE小19个基点。虽然引入货币政策变动的模型三的标准差与模型二的预测误差的标准差几乎相等,但相对于模型一与AR(1)模型,其预测误差的标准差更小。综合来看,货币政策的变动能够在一定程度上解释短期市场利率的跳跃现象,引入货币政策变动的GARCH—JUMP模型有助于预测短期市场利率。

表5 各模型的预测误差均方误
六、结论与建议
(一)主要结论
本文以隔夜SHIBOR为例,构建一个引入货币政策变动的短期市场利率的GARCH-JUMP模型,研究了法定存款准备金率变动与每周货币净投放是否在一定程度上造成了短期市场利率剧烈波动与跳跃,得到以下结论:
第一,货币政策变动有助于解释短期市场利率的跳跃现象,但是存款准备金率变动的影响具有时滞,每周货币净投放变动能够引起当期的短期市场利率跳跃。货币政策变动主要通过增加短期市场利率跳跃强度和大小,从而促使其发生剧烈的跳跃性现象。第二,相对于GARCH模型以及没有加入货币政策的GARCH-JUMP模型,引入每周货币净投放的GARCH-JUMP模型在短期市场利率发生跳跃的时点上具有最大的条件方差,且跳跃部分的条件方差解释了其条件方差的绝大部分。事前与事后的期望跳跃次数在短期市场利率发生巨大跳跃时也会相应增加,这些都说明该模型具有很好的拟合效果。第三,从预测结果看,引入每周货币净投放的GARCH-JUMP模型在预测短期市场利率动态方面有最高的拟合优度与最小的均方误。这进一步说明货币政策变动在一定程度上有助于解释短期利率的剧烈波动。
(二)政策建议
本文的研究对于利率市场化后我国的货币政策操作具有一定的指导意义,对货币市场参与者也有重要的参考价值。一方面,正如美联储通过公开市场操作调控联邦基金利率以影响金融市场的资金供求,进而影响实体经济一样,利率市场化后中国将不可避免地需要进行类似操作。本文的研究结论显示中国央行的公开市场操作能够显著影响SHIBOR,很多相关文献也证实SHIBOR可以担当市场基准利率的重任。另外,以SHIBOR作为定价参考标准的金融产品越来越多,在可以预见的将来,我们有理由相信SHIBOR将成为中国货币政策操作的基准利率。基于此,我们建议学术界和央行要密切关注并研究SHIBOR的波动规律、影响其波动的各种因素以及其期限结构等,进而找出货币政策操作影响SHIBOR的路径和机制,以便制定更加有效的货币政策。另一方面,利率市场化后,各商业银行及其它金融机构都面临参照利率的选择问题。SHIBOR目前的报价行已经涵盖中国境内的所有大型商业银行,基本上可以反映资金市场的供求情况,其作为金融市场参考利率的作用将会凸现。在此背景下,仔细研究SHIBOR的动态过程(尤其是其剧烈的跳跃现象)对商业银行和其它金融机构的资产管理、风险管控甚至产品设计都将至关重要。
当然本文也存在着一些不足,例如我们的模型没有引入其它宏观变量,如货币供应量和投资变动等,也没有考虑国际资本流动对SHIBOR的影响。这主要由于宏观变量的数据都是月度或者更低频的,很难与高频利率数据匹配。此外,构建更复杂的VAR或DSGE模型,从而对货币政策、货币市场与宏观经济变量进行系统的分析也许可以帮助我们更好的理解货币政策与短期市场利率的关系。
参考文献:
[1]冯根福. 中国当前经济社会发展重大问题的四点思考[J]. 当代经济科学, 2015(3): 1-8+124.
[2]涂巍, 王治国, 邹恒甫. 转型期的中国经济波动特征[J]. 统计研究, 2014(4): 8-13.
[3]方意, 方明. 中国货币市场基准利率的确立及其动态关系研究[J]. 金融研究, 2012(7): 84-97.
[4]于建忠, 刘湘成. Shibor定价理论模型研究及其应用[J]. 金融研究, 2009(2): 40-53.
[5]Vasicek O. An equilibrium characterization of the term structure [J]. Journal of Financial Economics, 1977, 5(2): 177-188.
[6]Cox J C, Ingersoll J E, Ross S A. A theory of the term structure of interest Rates [J]. Econometrica, 1985, 53(2): 385-407.
[7]Chan K C, et al. An empirical comparison of alternative models of the short-term interest rate [J]. Journal of Finance, 1992, 47(3): 1209-1227.
[8]Ait-Sahalia Y. Testing continuous-time models of the spot interest rate [J].Review of Financial Studies, 1996, 9(2): 385-426.
[9]Longstaff F A, Schwartz E S. A two-factor interest rate model and contingent claims valuation [J]. The Journal of Fixed Income, 1992, 2(3): 16-23.
[10]Duffee G R. Term premia and interest rate forecasts in affine models [J]. Journal of Finance, 2002, 57(1): 405-443.
[11]Duffie D, Singleton K J. An econometric model of the term structure of interest-rate swap yields [J]. Journal of Finance, 1997, 52(4): 1287-1321.
[12]Brenner R J, Harjes R H, Kroner K F. Another look at models of the short-term interest rate [J]. Journal of Financial and Quantitative Analysis, 1996, 31(1): 85-107.
[13]Anderson T G, Lund J. Estimating continuous-time stochastic volatility models of the short-term interest rate [J]. Journal of Econometrics, 1997, 77(2): 343-377.
[14]Gray S F. Modeling the conditional distribution of interest rates as a regime-switching process [J]. Journal of Financial Economics, 1996, 42(1): 27-62.
[15]Ang A, Bekaert G. Regime switches in interest rates [J]. Journal of Business & Economic Statistics, 2002, 20(2): 163-182.
[16]Hamilton J D. A new approach to the econometric analysis of nonstationary time series and the business cycle [J]. Econometrica, 1989, 57(2): 357-384.
[17]Das S R. The surprise element: Jumps in interest rates [J]. Journal of Econometrics, 2002, 106(1): 27-65.
[18]Johannes M. The statistical and economic role of jumps in continuous-time interest rate models [J]. Journal of Finance, 2004, 59(1): 227-260.
[19]王建喜, 王晓轩. 基于我国国债的利率期限结构曲线估计[J]. 当代经济科学, 2004(5): 43-46+51-109.
[20]梁琪, 张孝岩, 过新伟.中国金融市场基准利率的培育——基于构建完整基准收益率曲线的实证分析[J].金融研究, 2010(9): 87-105.
[21]谢赤, 吴雄伟. 基于Vasicek和CIR模型中的中国货币市场利率行为实证分析[J]. 中国管理科学, 2012(3): 22-25.
[22]洪永淼, 林海. 中国市场利率动态研究——基于短期国债回购利率的实证分析[J]. 经济学季刊, 2006(2): 512-531.
[23]张金清, 周茂彬. 中国短期利率跳跃行为的实证研究[J]. 统计研究, 2008(1): 59-64.
[24]Chan W H, Maheu J M. Conditional jump dynamics in stock market returns [J]. Journal of Business & Economic Statistics, 2002, 20(3): 377-389.
[25]彭兴韵, 施华强. 货币市场对货币政策操作的反应——中国的实证研究[J]. 金融研究, 2007(9): 20-30.
[26]张雪莹. 存款准备金率调节对市场利率的影响效应研究[J]. 数量经济技术经济研究, 2012(12): 136-146.
[27]谢平, 罗雄. 泰勒规则及其在中国货币政策中的检验[J]. 经济研究, 2002(3): 3-12+92.
责任编辑、校对:郭燕庆
The Effects of Monetary Policy on the Dynamic Process of Short-term Market Interest Rate—An Empirical Research Based on SHIBOR
LIU Hong-kui1,WANG Zhi-guo2,ZOU Heng-fu1
(1.China Economics and Management Academy, Central University of Finance and Economics, Beijing 100081, China;2. Guanghua School of Management, Peking University, Beijing 100871, China)
Abstract:Based on Shanghai Inter-bank Offered Rate (SHIBOR), this paper introduces GARCH-JUMP model on the effects of monetary policy on short-term market interest rate and empirically studies whether the change of monetary policy can make SHIBOR have sharp jumping phenomenon. Research finds: (1) the change of monetary policy is conductive to explaining the jump of short-term market rate. Time lag of the effects of reserve requirement ratio change on SHIBOR exists and the weekly net money input can lead to instantaneous interest jump ;(2)the introduced model on weekly net money input has the largest condition variance at the time point when SHIBOR jumps and the condition variance explains most of the variance. The condition variance of GARCH part is relatively small; (3)the ex-ante and ex-post expected jump times in GARCH-JUMP model increases correspondingly when SHIBIOR jumps violently;(4)the prediction outside sample indicates that GARCH-JUMP model has the best fitness and least mean square deviation error in predicting the dynamic short-term market interest rate.
Key words:Monetary Policy; Open Market Operation; Short-term Market Interest Rates; SHIBOR; GARCH-JUMP Process;
文献标识码:A
文章编号:1002-2848-2016(02)-0030-11
作者简介:刘洪愧(1987-),湖南省耒阳市人,中央财经大学博士研究生,研究方向:货币政策、贸易政策;王治国(1977-),山东省德州市人,北京大学光华管理学院讲师、管理学博士,研究方向:应用博弈论、货币政策等;邹恒甫(1962-),湖南省华容县人,1989年毕业于哈佛大学,经济学博士,现为中央财经大学中国经济与管理研究院院长、教授、博士生导师,世界银行研究部终身高级经济学家,研究方向:经济增长、转型经济研究、货币政策等。
基金项目:本研究受国家社科基金项目(项目编号:13CJY093)资助。
收稿日期:2015-11-14

