基于路径与深度的同义词词林词语相似度计算
陈宏朝,李 飞,朱新华,马润聪
(广西师范大学 多源信息挖掘与安全重点实验室,广西 桂林 541004)
基于路径与深度的同义词词林词语相似度计算
陈宏朝,李 飞,朱新华,马润聪
(广西师范大学 多源信息挖掘与安全重点实验室,广西 桂林 541004)
该文提出了一种基于路径与深度的同义词词林词语语义相似度计算方法。该方法通过两个词语义项之间的最短路径以及它们的最近公共父结点在层次树中的深度计算出两个词语义项的相似度。在处理两个词语义项的最短路径与其最近公共父结点的深度时,为提高路径与深度计算的合理性,为分类树中不同层之间的边赋予不同的权值,同时通过两个义项在其最近公共父结点中的分支间距动态调节词语义项间的最短路径,从而平衡两个词语的相似度。该方法修正了目前相关算法只能得出几个固定的相似度值,所有最近公共父结点处于同一层次的义项对之间的相似度都相同的不合理现象,使词语语义相似度的计算结果更为合理。实验表明,该方法对MC30词对的相似度计算值与人工判定值相比,取得了0.856的皮尔逊相关系数,该结果高于目前大多数词语相似度算法与MC30的相关度。
同义词词林;路径;深度;分支间距;最近公共父结点
1 引言
词语语义相似度的计算是自然语言处理的重要研究内容,在智能检索、词义排歧、自动问答和机器翻译等领域都有广泛的应用,它是一个基础研究课题,正在被越来越多的研究人员所关注。目前词语相似度计算的研究策略大体分为两类[1]: 一类是根据某种世界知识来计算,主要是基于概念间结构层次关系组织的语义词典的方法,根据在这类语言学资源中概念之间的上下位关系和同位关系来计算词语的相似度;另一类是利用大规模的语料库进行统计,这种基于统计的方法主要将上下文信息的概率分布作为词语语义相似度的参照依据。
目前可为英文词语的语义相似度计算提供支持的语义词典主要有WordNet[2]、FrameNet[3]、MindNet[4]等。可为汉语词语语义相似度计算提供支持的语义词典主要有《知网》[5]、《同义词词林》[6]、《中文概念词典》[7]等。
关于相似度的概念,Dekang Lin认为任何两个对象的相似度取决于它们的共性(commonality ) 和个性(differentces)[8], 他从信息理论的角度给出任意两个对象相似度的通用公式如式(1)所示。
(1)
其中分子是描述A、B共性所需要的信息量大小。分母是完整的描述出A、B所需要的信息量大小。Dekang Lin 的这一理论是目前绝大多数基于语义词典的方法的词语相似度计算模型的基本思想[9]。
目前,国内中文词语相似度计算的相关研究主要采用《知网》作为分类词典[9-11],采用《同义词词林》的相关研究较少。事实上,《同义词词林》是目前国内在结构上与著名英文语义词典WordNet最为接近的一个分类词典[12],而国际上许多著名的词语相似度算法[13-15]都是采用WordNet作为分类词典,因此《同义词词林》在中文词语相似度计算的研究中是大有潜力的。目前,基于《同义词词林》的词语相似度计算研究主要有:田久乐[16]利 用《同 义 词 词林》提出的综合词语距离与分支层间隔的词语相似度计算方法;耿端[17]提出的基于边权重的同义词词林词语相似度计算方法。这两种方法在国际标准测试集MC30中的相似度测量值与人工判定值的皮尔逊相关系数偏低,与国际上优秀的基于路径和深度的算法相比还有一定的差距。
2 相关知识
2.1 同义词词林简介
同义词词林是由梅家驹[6]等人于1983年编撰的可计算汉语词库,其设计目标是实现汉语同义词和同类词的划分和归类。同义词词林经哈尔滨工业大学信息检索研究室的扩展后,目前共有七万多个词语,这些词语被分为了12个大类,95个中类,1 428个小类,小类下方进一步划分为4 026个词群和17 797个原子词群两级[18]。为便于处理不同大类的词语对,本文为所有大类虚构了一个根结点O,从而形成图1所示的六层树形结构。
同义词词林中上面四层的结点都代表抽象的类别,只有最底层的叶子结点才是一个个具体的词条或义项[12],同一个词条可能在不同的类别中同时存在,即词条的义项编码不是唯一的。第一至三大类多属名词,数词和量词在第四大类中,第五类多属形容词,第六至十类多是动词,十一类多属虚词,十二类是难以被分到上述类别中的一些词语。大类和中类的排序遵照具体概念到抽象概念的原则[6]。
关于词条的编码如表1所示。第八位编码只有三种情况,“=”代表“相等”、“同义”。“#”代表“不等”、“同类”,属于相关词语。“@”代表“自我封闭”、“独立”,它在词典中既没有同义词也没有相关词[6]。前七位编码就可以唯一确定一条编码,即不存在这种情况: 前七位编码相同而第八位不相同的多条编码同时存在。当前七位编码确定以后,第八位就是固定的,要么是“=”,要么是“#”,要么是“@”。例如,(乔木,灌木,林木)这一组同义词在词林中的编码为“Bh01A68#”。
本研究使用的同义词词林是哈尔滨工业大学发布的《哈工大信息检索研究室同义词词林扩展版》的 1.0 版本。

表1 词林中词语的编码结构
2.2 基于路径和深度的方法介绍
基于路径和深度的方法目前已广泛应用于基于WordNet的英语词语相似度计算。Wu等人[19]在机器翻译作词语选择问题的时候,提出了这种方法。他们定义词语义项s1和s2的相似度计算公式如式(2)所示。
(2)
这里N1和N2分别表示义项s1和义项s2到他们最近公共父结点的路径距离,H表示义项s1和s2最近公共父结点到根结点的距离,即深度。
Hao等人[20]也利用两个词语义项的最短路径跟它们的最近公共父结点的深度来计算两个词语在WordNet中的相似度,其词语义项s1和s2相似度计算公式如式(3)所示。
(3)
这里d表示两个词语义项之间的路径距离,h表示它们最近公共父结点的深度,α和β是平滑参数。当h=0的时候,将两个词语义项间的相似度处理为0,α的取值范围在0-1之间,每次的变化步长为0.1,β每次变化的步长为1。他们通过实验得出当α=0,β=1的时候相似度取值最合理。
Liu等人[21]提出了一种改进式(2)的计算相似度方法。他们方法的基本思想是基于人工判定的方法,用词语义项s1和s2的共同特性与它们二者总的特性的比值作为两个词语义项的相似度,提出相似度计算公式如式(4)所示。
(4)
这里l是词语义项s1和s2的最短路径,d是最近公共父结点的深度,α和β是平滑参数且(0<α,β<1),它们通过实验得出式(4)中的参数α=0.5,β=0.55,但在实际测量时,存在对于不同大类之间的词的相似度都为0的现象。
田久乐[16]提出了一种变异的基于路径和深度的同义词词林词语相似度计算方法,对于两个词语义项s1和s2,其相似度计算公式如式(5)所示。
(5)
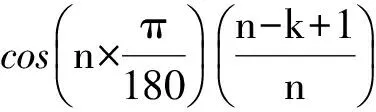
3 基于路径和深度的同义词词林词语相似度的计算方法
3.1 基于路径和深度的词林词语相似度公式的提出
Wu等人[19]是最早在式(1)的思想之上采用路径与深度来计算词语相似度的,他们提出了式(2)计算两个词语的相似度,但是该公式对路径与深度未使用任何动态调节参数,这在叶子结点深度不均匀、义项遍布所有结点的WordNet中是可以反映出多数义项对之间的差异性的,但词林的所有义项都在叶子结点且所有叶子结点的深度相同,因此如果直接在同义词词林中应用该公式,只能得出0,0.2,0.4,0.8,1等几个固定的相似度值,这样所有最近公共父结点处于同一层次的义项对之间的相似度都相同,这与实际情况不相符;同样,Hao等人[20]提出的式(3)与Liu等人[21]提出的式(4),由于只采用了固定参数来调节路径与深度,因此应用于同义词词林也只能得出几个固定的相似度值,无法进一步反映出公共父结点处于同一层次的义项对之间的差异性。
为解决上述问题,本文提出一种新的基于一个动态调节参数的词语相似度计算方法。首先,根据式(1)的思想,我们提出在语义词典中任意两个义项概念s1和s2的特性与相似度的关系为式(6)。
(6)
其中,comm(s1,s2)表示两个义项s1和s2在语义词典中的共同特性,diff(s1,ss)表示s1和s2在语义词典中的差异特性。
在词林中,对任意两个词语义项s1和s2,它们在树形图中的关系可以抽象为图2所示。O为树的根结点,LCP为义项s1和s2的最近公共父结点,Path1、Path2分别为义项s1和s2到它们最近公共父结点的路径距离,Depth为s1、s2最近公共父结点到根结点的深度距离。
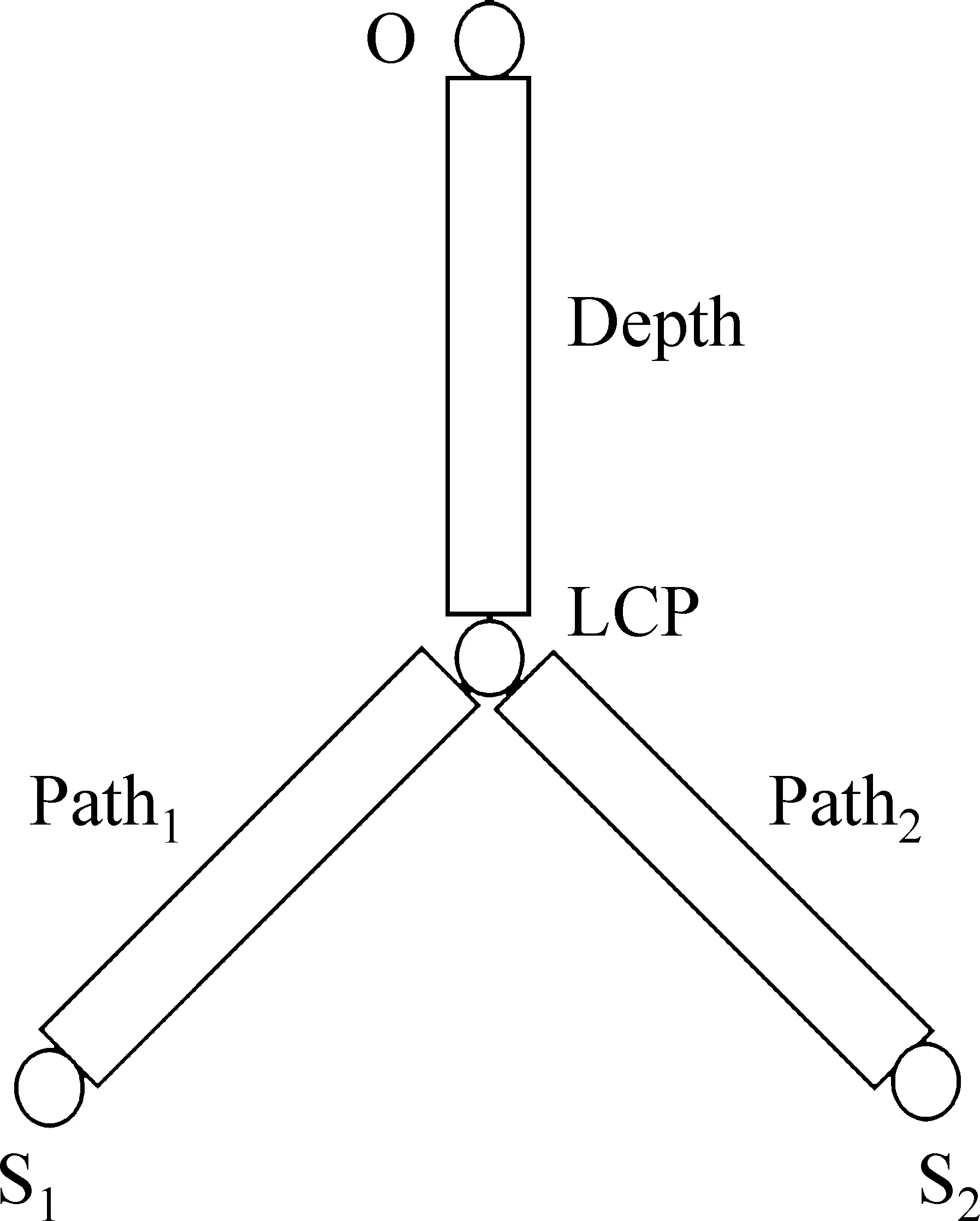
图2 词林树形结构抽象图
由图2,我们提出对于任意两个义项s1和s2在词林中的共性与差异性的计算公式为式(7)、式(8)。
其中,Path(s1,s2)=Path1+Path2,表示两个义项之间的最短路径;α为深度调节参数,β为路径调节参数。将式(7)、式(8)代入式(6),可以得到任意两个义项s1、s2的相似度计算公式为式(9)。
(9)
当两个义项的编码相同且处于“=”后面时,表示两个义项为同义词,他们相似度被处理为1;当两个义项的编码相同且处于“#”后面时,表示两个义项为同类词,他们相似度被处理为0.5。
考虑到有的词语会有多个义项,两个词语的最终相似度取所有义项对中相似度最大者。设词语w1有m个义项,词语w2有n个义项,则词语w1与w2在同义词词林中的相似度计算公式为式(10)。
(10)
其中,sim(s1i,s2j)表示词语w1的第i个义项与w2的第j个义项的相似度值。
3.2 路径和深度的计算公式
为确保义项路径距离计算的合理性,本文借助文献[1]的思想在词语路径与深度的计算公式中引入了边权重概念。本文为图1所示的同义词词林结构中五条不同层次之间的边,从下到上分别设定权重Weight(i)(1≤i≤5)(对应图1中的WT1、WT2、WT3、WT4、WT5),且满足:
其中,设图1中最底部的叶子结点的层编号为0,最上面根结点层编号为5,Weight(i)为上层编号为i的边的权重。
于是,设义项s1和s2的最近公共父结点LCP处于第k层且到根结点共有m条边相连,则LCP的深度距离Depth(LCP(s1,s2))的计算公式如式(11)所示。
(11)
由于在词林中,所有词语义项都处于最低的叶子层,因此任意两个义项到其最近公共父结点的距离都是相同的。设义项s1、s2到其最近公共父结点分别有n条边相连,则义项s1与s2之间的最短路径距离Path(s1,s2)的计算公式如式(12)所示。
(12)
3.3α和β参数的取值
在同义词词林的分类树中,不同大类词语义项的公共父结点为本文所虚拟的根结点,而根结点的深度Depth =0,为了避免不同大类词语义项间的相似度为0,我们假定根结点的深度为α(α∈[0,1])。
在词林语义词典中,每个分类结点下方分支结点的排列与编码具有一定规律,图3给出了在词林分类结构中,最近公共父结点为第四层“Ae02A 工人类”的分支结点排列与编码示例。
图3中,第五层中的词语编码从左到右依次递增编码,例如,“工人”的编码为Ae02A01,“工匠”的编码为Ae02A02,“师傅”的编码为Ae02A03,…,“画匠”的编码为Ae02A13,…,“工程建设者”的编码为Ae02A24。从图3可以看出,在分支层中,分支结点的编码一般遵循从抽象类到一般的原则,且间距越近的两个概念意义越接近,该规律同样出现在最近公共父结点处于更高层次的分支结点中。于是我们能够得出两个词语义项的相似度与其在最近公共父结点中的分支间距线性负相关。另一方面,在语义词典的分类结构中,每个分类结点下面的直接孩子数N差别很大,因此我们取用两个义项在分支层的相对间距作为路径调节参数β,并将其视作义项之间路径的延伸,如式(13)所示。
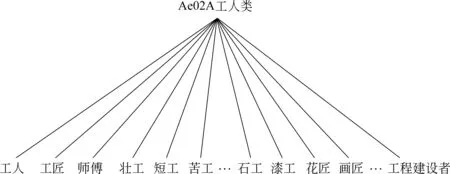
图3 词林分支结构实例
(13)
其中,i为分支结点B1,B2所在层的编号(图4),Weight(i)为连接分支结点与最近公共父结点的边权重,N表示两个义项最近公共父结点(LCP)的直接孩子的个数,K表示两个义项在最近公共父结点中的分支间距,比如在图4中,s1与s2这两个词语义项之间的K=2,N=5。
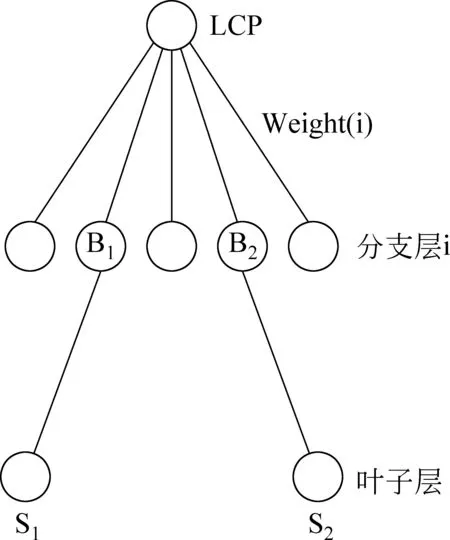
图4 分支间距示意图
4 实验与分析
目前国际上对词语相似度算法的评价标准普遍采用Miller & Charles(MC)发布的英语普通名词数据集(Common nouns dataset)及其人工判定值[22]。该数据集分别由高度相关、中度相关与低度相关共30个英语词对组成,并让38个试验者对数据集进行语义相似度判断,最后取他们的平均值作为人工判定值。Miller & Charles发布的英语普通名词数据集来源于Rubenstein & Goodenough(RG)[23]发布的65对名词数据集。虽然Miller & Charles的实验比Rubenstein & Goodenough实验晚25年左右,但是这两个数据集的皮尔逊相关系数却是达到了0.97,这说明人对词语间的语义相似度的认识随着时间的流逝还是比较稳定的,人对词语间的评判值可以被当作评估词语语义相似计算方法的依据。
在本文中,考虑到国际标准测试集MC30在评判词语相似度方法中的流行程度,我们将Rubenstein & Goodenough的65对词分割成两部分: 一部分包含MC和RG共同使用的30对词,定义为集合D0;另一部分包含RG65对词中剩余的35对词,定义为集合D1。为了确保实验结果的客观性,我们使用集合D1去训练我们的计算公式,对参数α和β进行优化处理,然后再用集合D0去测试我们的方法。
4.1 α和β参数的确定
首先,将训练集合D1中的35对英语词对按照意义最接近的原则翻译成对应的中文名词词对(表2),然后在训练集合D1中不断地改变参数α以及参数β中的权值,最后比较参数α和权值改变时计算的相似度值与Rubenstein & Goodenough的人工判定值的皮尔逊相关系数,当皮尔逊相关系数达到最大时,所用的参数α和权重即为我们确定的参数值。通过实验我们确定参数α=0.9,权重函数Weight(i)按照表3取值时效果最好,皮尔逊相关系数为0.8615,数据如表2所示。
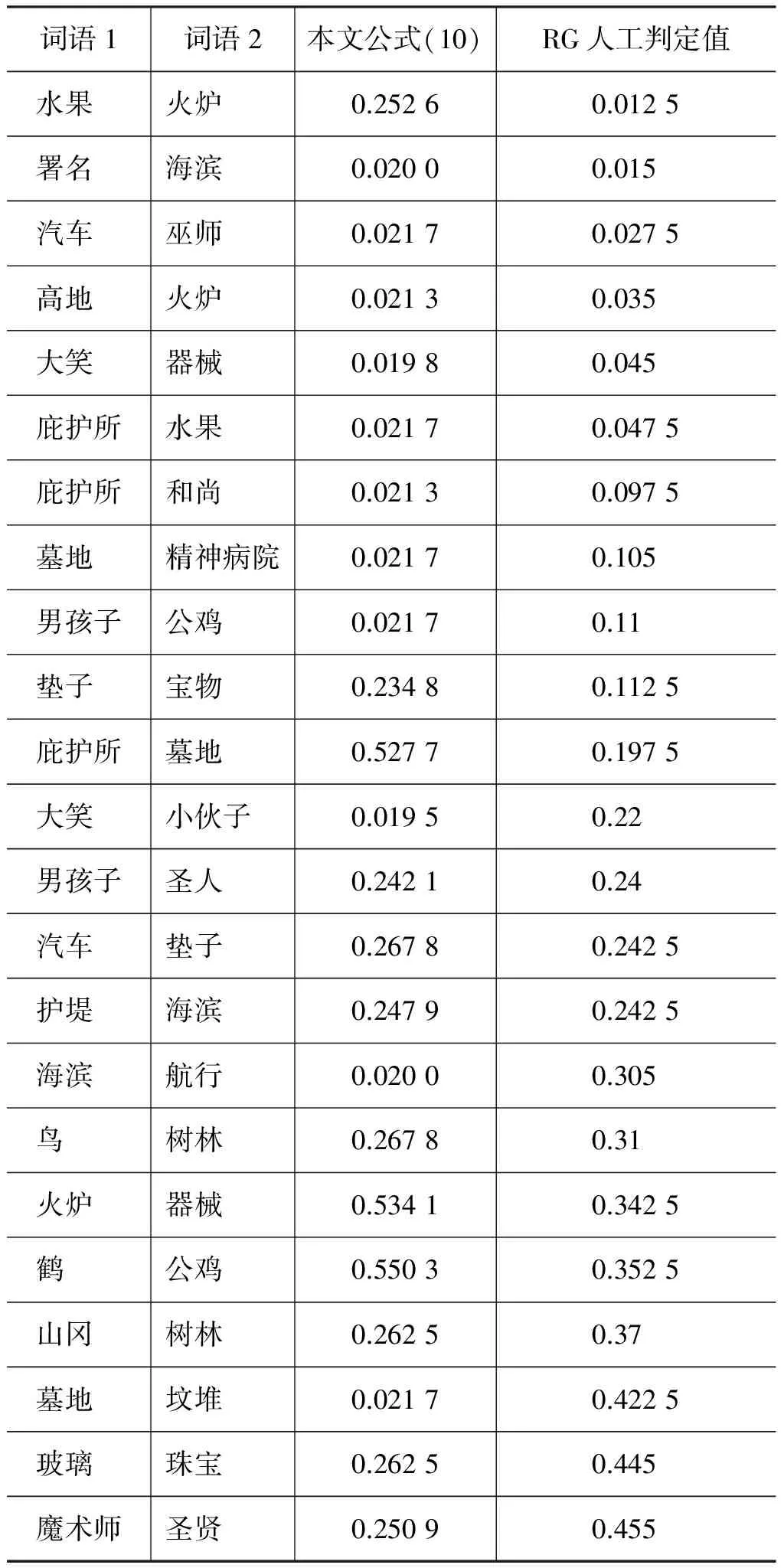
表2 D1数据集中的最佳计算结果
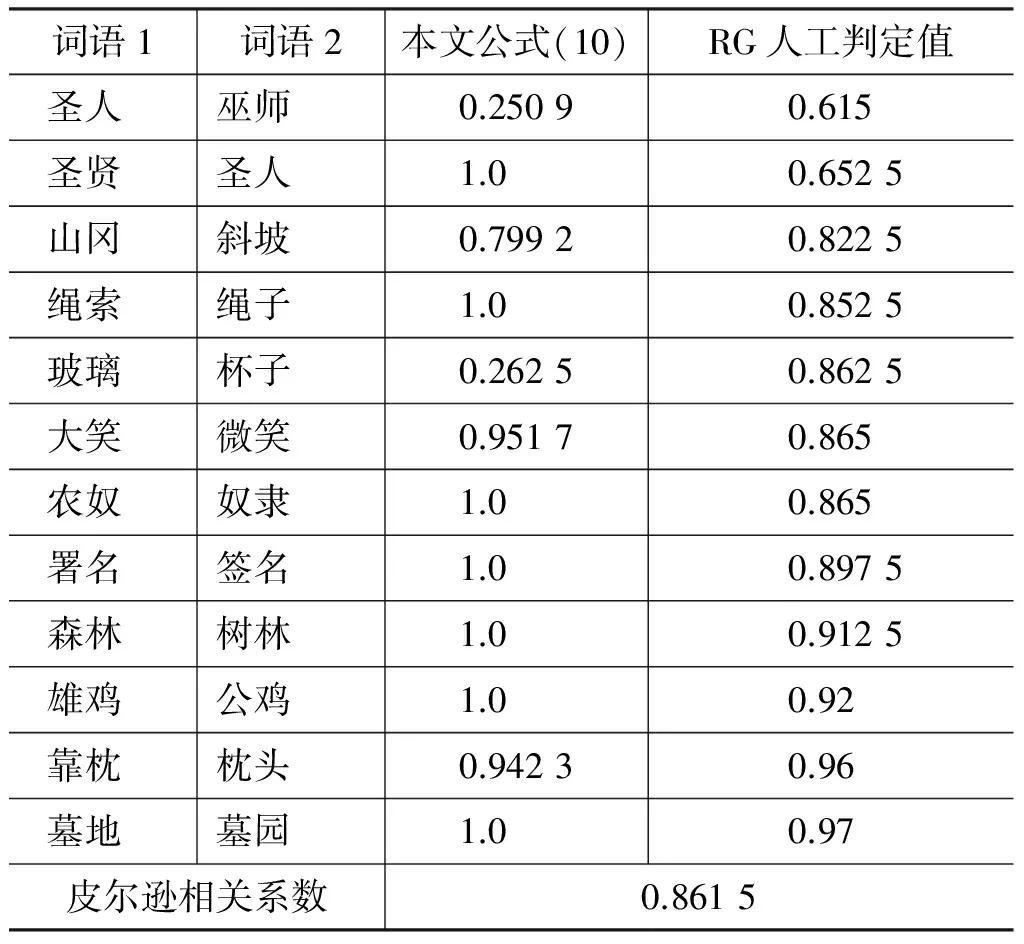
续表

表3 边权重函数的最佳离散值
4.2 对比实验
本文采用Miller & Charles(MC)发布的数据集及其人工判定值作为标准,比较本文提出的式(10)与Wu等人提出的式(2)和Hao等人提出的式(3)、Liu等人提出的式(4)以及田久乐提出的式(5)的词语相似度计算结果。首先,将测试集合D0中的30个英语词对按照意义最接近的原则翻译成对应的中文名词词对,然后采用不同的公式对该数据集计算相似度(表4),最后计算出不同公式的相似度计算值与MC人工值的皮尔逊相关系数(表5)。为增加结果的可比性,表5还列出了若干英文词语相似度算法与MC30人工判定值的皮尔逊相关系数。
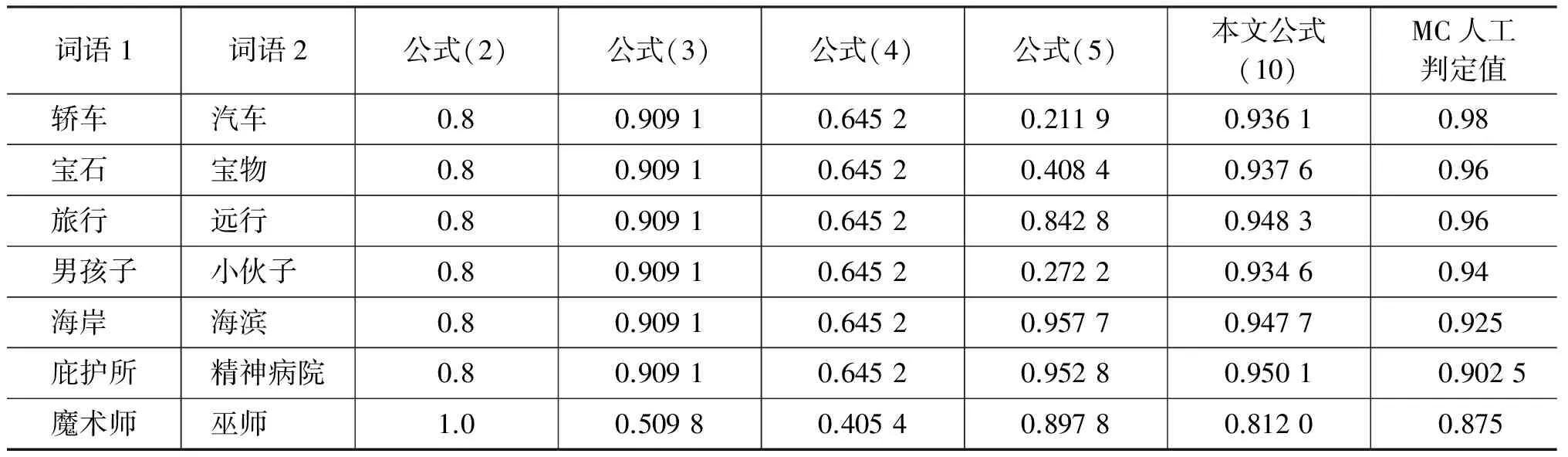
表4 Miller词对集的计算结果对比
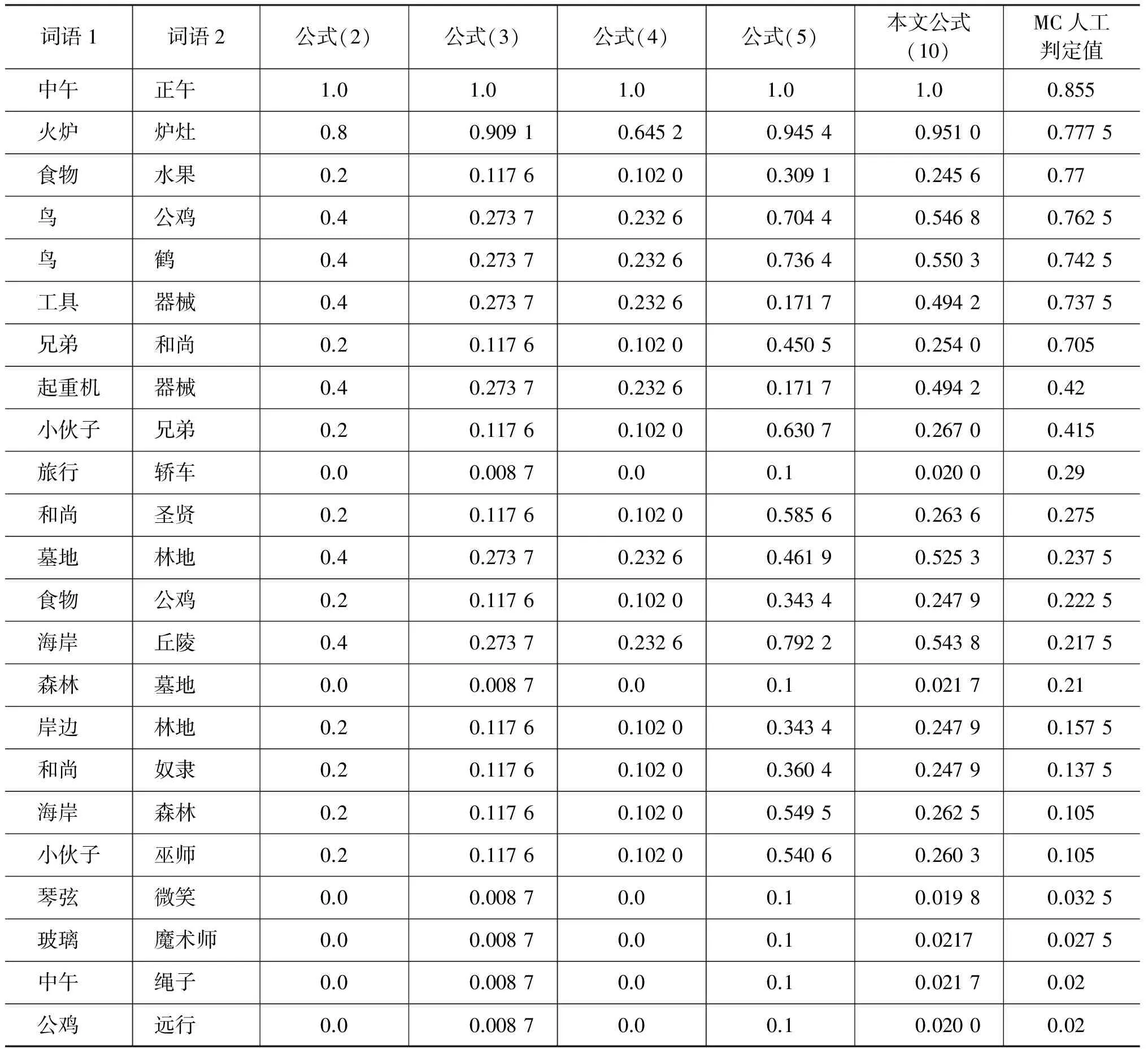
续表
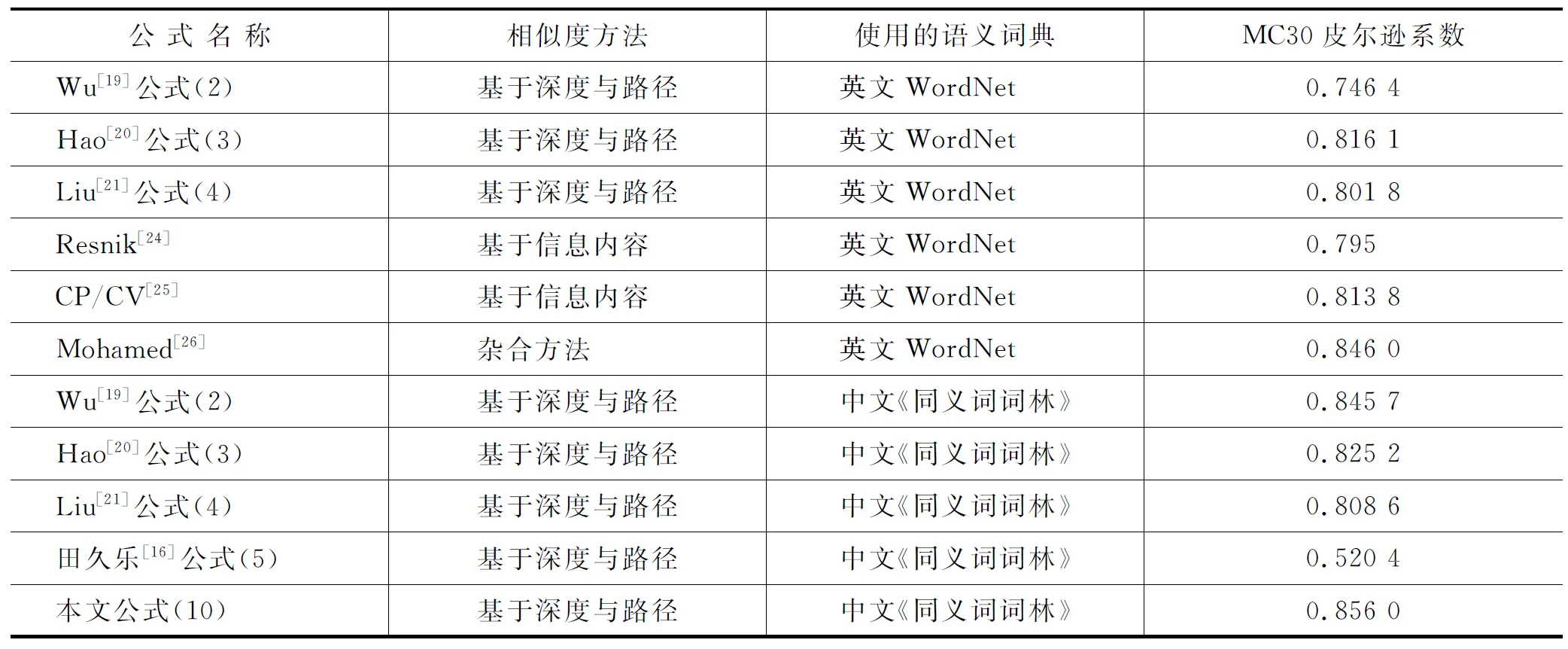
表5 不同方法与MC人工值的皮尔逊相关系数
4.3 结果分析
通过上述实验与实例,可以得出以下结论。
(1) 从上述对比实验可以看出: 效果最好的是本文提出的基于路径和深度的同义词词林词语语义相似度计算方法,所得出的相似度值的覆盖范围最广,且与MC30人工值的皮尔逊相关系数达到了0.856,该值高于目前国内外大多数词语相似度算法。本文方法与MC30皮尔逊相关系数比较高的原因是,本文公式严格遵循了任意两个对象相似度的通用公式的思想,并且通过采用动态边权重,调高了最近公共父结点层次较低的词语相似度的值(表4中的前九对词语),而同时调低了最近公共父结点层次较高的词语相似度的值(表4中的最后九对词语),从而使计算结果更加符合实际情况。
(2) 式(2)、(3)与(4)的方法在计算相似度时,只能得出五个固定的相似度值,所有最近公共父结点处于同一层次的义项对之间的相似度都相同,这与实际应用情况不相符,本文方法通过一个基于分支间距的动态路径调节参数β避免了这种现象。同时,本文方法通过一个深度调节参数α,避免了表4中最后四对跨大类的词语相似度为0的现象。
(3) 田久乐提出的式(5)的计算结果,与MC人工值的皮尔逊相关系数只有0.520 4,主要是由于该公式直接使用分支间距作为相似度的调节参数,从而使公式对词语在最近公共父结点中的分支间距过于敏感,造成分支间距较大的词对的相似度值过低,如在计算“轿车”与“汽车”、“男孩子”与“小伙子”两个词对的相似度时,由于他们在最近公共父结点中的分支间距过大,造成了他们的相似度过低。而在本文的方法中,分支间距只是作为义项之间路径的延伸,从而降低了对该值的敏感度,提高了词语相似度的准确度。
(4) 在表4中,所有方法在计算“食物”与“水果”词对的相似度时与MC人工值相比都偏低,这主要是在同义词词林分类结构中,将“食物”归为第二大类“物”中的“粮食”中类而将“水果”归为“物”的“草木”中类,造成二者的公共父结点的层次过高。“兄弟”与“和尚”词对的相似度计算结果过低,也是他们在同义词词林分类结构中公共父结点的层次过高造成的。
(5) 通过表5可以看出,同样的式(2)、式(3)、式(4)在同义词词林中的MC30皮尔逊相关系数要高于其在英文WordNet中的结果,这说明同义词词林的简明分类结构要优于WordNet的复杂分类结构,因此只要有优秀的应用算法相配合,同义词词林在中文信息处理中是可以大有作为的。
5 结束语
本文提出了一种新的基于路径与深度的词语相似度计算方法,合理地利用了两个词语在树形结构中的最短路径、最近公共父结点的深度与分支间距等因素。实验证明,该方法计算出的词语相似度与人工判定值高度相似,在相关领域具有较好的实用价值。我们也发现有一些词语无论用哪种方法计算结果均不理想,这种情况主要是词语在词典结构中的分类不合理造成的,这需要修正词典的分类结构才能解决。我们下一步打算进一步引入最近公共父结点的信息内容对本文方法进行优化。
[1] 葛斌,李芳芳,郭丝路,等大权. 基于知网的词汇语义相似度计算方法研究[J].计算机应用研究,2010,09: 3329-3333.
[2] G A Miller, C Fellbaum. Semantic network of English [M], B. Levin (Ed.), lexical & conceptual semantics, Amsterdam: Elsevier Science Publishers, 1991.
[3] C F Baker. The BerkeleyFrameNet project[C]// Proceedings of the COLING-ACL, Montreal, Canada, 1998: 86-90.
[4] S D Richardson, W B Dolan.MindNet: Acquiring and structuring semantic information from text[C]// Proceedings of COLING-ACL, Quebec, Canada, 1998: 1098-1102.
[5] 董振东.语义关系的表达和知识系统的建造[ J ].语言文字应用, 1998, 03: 76-83.
[6] 梅家驹, 等. 同义词词林[M]. 上海: 上海辞书出版社出版, 1983.
[7] 于江生,俞士汶.中文概念词典的结构[ J ].中文信息学报, 2002,16(4): 12-20.
[8] Dekang Lin. An Information Theoretic Definition of Similarity Semantic distance in WordNet[C]//Proceedings of the Fifteenth International Conference on Machine Learning, Madison, Wisconsin, USA,1998: 928-933.
[9] 张亮,尹存燕,陈家骏.基于语义树的中文词语相似度计算与分析[J].中文信息学报,2010,24(6): 23-29.
[10] 刘群,李素建.基于《知网》的词汇语义相似度计算[C].台北: 第三届汉语词汇语义学研讨会, 2002: 59-76.
[11] 江敏,肖诗斌,王弘蔚,等. 一种改进的基于《知网》的词语语义相似度计算[J]. 中文信息学报,2008,22(5): 84-89.
[12] 梅立军,周强,臧路,等. 知网与同义词词林的信息融合研究[J].中文信息学报,2005,19(1): 63-70.
[13] Mohamed AliHadj Taieb, Mohamed Ben Aouicha, Abdelmajid Ben Hamadou. A new semantic relatedness measurement using wordnet features [J]. Knowledge and Information Systems, 2014, 41(2): 467-497.
[14] L Meng, J Gu, Z Zhou. A new model of information content based on concept's topology for measuring semantic similarity in WordNet [J]. Journal of Grid & Distributed Computing, 2012, 5(3): 81-96.
[15] Z Zhou, Y Wang, J Gu. A new model of information content for semantic similarity in WordNet[C]//Proceedings of the International Conference on the Future Generation Communication and Networking Symposia, Sanya, China, 2008: 85-89.
[16] 田久乐,赵蔚.基于同义词词林的词语相似度计算方法[J].吉林大学学报(信息科学版),2010,06: 602-608.
[17] 耿端.基于同义词词林的评分在中医案例自测系统中的应用[D]. 西北大学硕士学位论文,2013.
[18] 刘丹丹,彭成,钱龙华,等.《同义词词林》在中文实体关系抽取中的作用[J]. 中文信息学报,2014,28(2): 91-99.
[19] Z. Wu, M. Palmer. Verbs semantics and lexical selection [C]// Proceedings of the 32nd Annual Meeting on Association for Computational Linguistics, ACL'94, Association for Computational Linguistics, Stroudsburg, PA, USA, 1994: 133-138.
[20] D.Hao, W. Zuo, T. Peng. An approach for calculating semantic similarity between words using wordnet [C]//Proceedings of the second International Conference on Digital Manufacturing and Automation, Zhangjiajie, China, 2011: 177-180.
[21] X. Liu, Y. Zhou, R.Zheng. Measuring semantic similarity in WordNet[C]//Proceedings of the Sixth International Conference on Machine Learning and Cybernetics, Hong Kong, China, 2007: 3431-3435.
[22] G.A. Miller, W.G. Charles. Contextual correlates of semantic similarity [J]. Language and Cognitive Processes, 1991, 6 (1): 1-28.
[23] H. Rubenstein, J.B.Goodenough. Contextual correlates of synonymy[C]//Proceedings of the ACM8(10), 1965: 627-633.
[24] P. Resnik. Semantic Similarity in Taxonomy: An Information-Based Measure and its Application to Problems of Ambiguity in Natural Language [J]. Journal of Artificial Intelligence Research, 1999, 11: 95-130.
[25] J W Kim, K S Candan. CP/CV: Concept similarity mining without frequency information from domain describing taxonomies [C]//Proceedings of the 15th ACM international conference on Information and knowledge management, New York, USA, 2006: 483-492.
[26] A H T Mohamed,B A Mohamed, A B Hamadou. Ontology-based approach for measuring semantic similarity [J]. Journal of Engineering Applications of Artificial Intelligence, 2014,36: 238-261.
A Path and Depth—Based Approach to Word Semantic Similarity Calcalation in CiLin
CHEN Hongchao,LI Fei,ZHU Xinhua, MA Runcong
(Guangxi Key Lab of Multi-source Information Mining & Security, Guangxi Normal University, Guilin,Guangxi 541004,China)
In this paper, we propose a word semantic similarity approach based on the path and depth in CiLin. This approach exploits the shortest path between two word senses and the depth of their lowest common parent node in the hierarchy tree to calculate the semantic similarity between two word senses. In order to improve the rationality of calculating the path and depth, we assign different weights to the edges between the different layers in classification tree, while dynamically adjusting the shortest path between two senses through their branch interval in the lowest common parent node. The experiments show that the correlation coefficient between the human judgments in MC30 dataset and the computational measures presented in this approach is 0.856, which is higher than those of most of current semantic similarity algorithms.
CiLin; path; depth; branch interval; lowest common parent node

陈宏朝(1963—),副教授,主要研究领域为自然语言处理、知识工程等。E⁃mail:chen7297@sina.com李飞(1990—),硕士研究生,主要研究领域为自然语言处理。E⁃mail:312078417@qq.com朱新华(1965—),通信作者,教授,主要研究领域为自然语言处理、智能教学系统等。E⁃mail:zxh429@263.net
1003-0077(2016)05-0080-09
2015-01-07 定稿日期: 2015-05-25
国家自然科学基金(61363036,61462010)

